An analysis of dynamic stability of an elastic column

M. Jin*

Department of Mechanics, School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China

1 Introduction

Dynamic stability of a compressed elastic column is a key problem in structure analysis. The problem has received considerable attention in early years, for examples, Woinowsky-Krieger[1], Brown et al. [2], Dickey [3], Reiss and Matkowsky [4], Tseng and Dugundji [5], Ball [6] and others. In recent years, Abou-Rayan et al. [7], Afaneh and Ibrahim [8], Nayfeh et al. [9], Chin and Nayfeh [10], Kreider and Nayfeh [11], Nayfeh and Emam [12-14],Mamandi et al. [15], Yang and Zhang [16], Emam and Abdalla[17], and Ghayesh and Farokhi [18] have been devoted to analyzing the non-linear response of buckled beams, which is still open for research. A basic problem is the dynamic stability of a column in straight shape in compression. Movchan [19] proved that a column is dynamically stable when compression load is smaller than the Euler load. However, in the sense of the Lyapunov stability, it is not clear theoretically up till now whether or not a column just at the first bifurcation point is dynamically stable and unstable when the load is greater than the Euler critical load. Not only the construction and analysis of the Lyapunov functional is the key problem in the dynamic stability of structures, but also the key problem in the other areas, such as control theory [20-22]. In this paper, by the Lyapunov functionals proposed by the author, the dynamic stability of two conservative systems is analyzed. The dynamic stability of a column with one end fixed and the other clamped in rotation is proved theoretically.

The paper is organized as follows：Section 2 is some basics,including definition in the sense of the Lyapunov stability, the Lyapunov theorems on dynamical stability and total energy of the column in vibration. Section 3 presents a conservative system of finite degree of freedom with a parameter, i.e. system I, an analysis of the dynamic stability of system I and a column with one end fixed and the other clamped in rotation when the load is smaller than or equals to the Euler critical load. Section 4 presents another conservative system of finite degree of freedom with a parameter, i.e. system II, an analysis of the dynamic instability of system II and the column when the load is greater the Euler critical load. Section 5 is conclusions.

2 Some basics

2.1 Lyapunov direct method

Consider a l-degree-of-freedom dynamical system, the state variable is denoted by

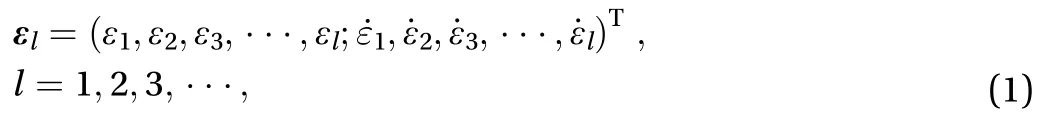
whereandare the general displacements and the general velocities, respectively. Vector=0 is the nullsolution or an equilibrium point of the -degree-of-freedom system. The Euclidean norm ofis

In the sense of Lyapunov, stable and unstable of the null solution=0on dynamic stability are defined as [23]:

1. The null solution is stable in the sense of Lyapunov if for any arbitrary positiveand time, there exists a η=η(γ，t0)＞ 0such that if the inequality

is satisfied, then the inequality

is implied.

2. The null solution is said to be unstable in the sense of Lyapunov if for any arbitrary small and any time such that

We have at some other finite time the situation

whereis a given arbitrary positive number. There are two sufficient conditions on stability and instability, respectively [23].

The Lyapunov stability theorem:If there exists a positivedefinite functionwhose total time derivativeis negative semi-definite along every trajectory of the system, then the trivial solution=0 is stable.is called the Lyapunov function, andis the total time derivative ofalong every trajectory of the system, where t is the time.

The Lyapunov instability theorem:If there exists for the system a functionwhose total time derivativeis positive-definite along every trajectory of the system and the function itself can assume positive values for an arbitrarily small values ofthen thetrivial solution=0 is unstable.is also called the Lyapunov function of the system.

2.2 Total energy of a column in vibration

An inextensible planar column with one end fixed and the other clamped in rotation is shown in Fig. 1.denotes the bending rigidity of the column, b denotes the length of the column before deformation, N denotes an axial compression load, w and θ denote lateral deflection and the tangential angle of the lateral deflection curve, respectively. s ∈ [0，b] and h ∈ [0，s]denote two arc-length coordinates with origin o on the axial line before deformation.

The total energy of the system is sum of potential energy and kinetic energy. Elastic potential energy equals to the strain energy. Dimensionless form of the strain energy is

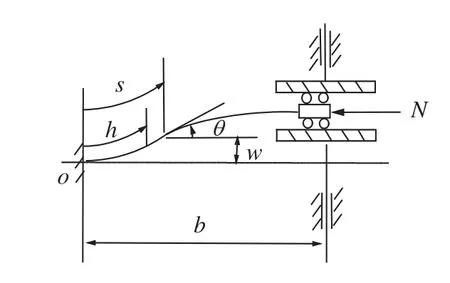
Fig. 1. An inextensible planar column with one clamped-end and the other clamped in rotation

whereandDimensionless form of potential N energy of the external force is

whereis the load factor. Dimensionless form of translational kinetic energy is

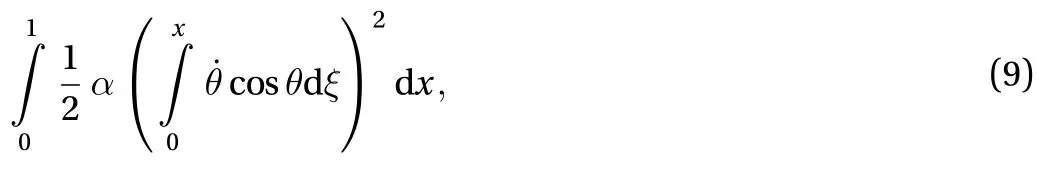
wherem is the mass per unit length of the column,is the angular velocity, andDimensionless form of rotational kinetic energy is

whereis the moment of inertia per unit length of the column.Summing up Eqs. (7)-(10), we have dimensionless form of the total energy of the system

Boundary conditions on the tangent angle of the column in Fig. 1 are

k=

The load factor at the first bifurcation point is . Considering conditions in Eq. (12), we have the Fourier series of the tangential angle

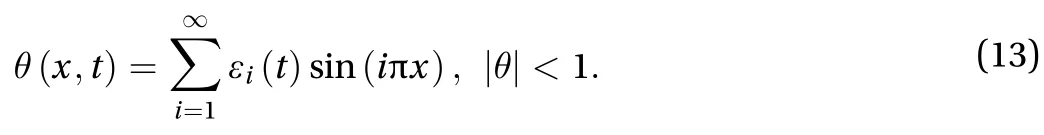
Based on the Hamilton principle, trajectory of the system makes functional

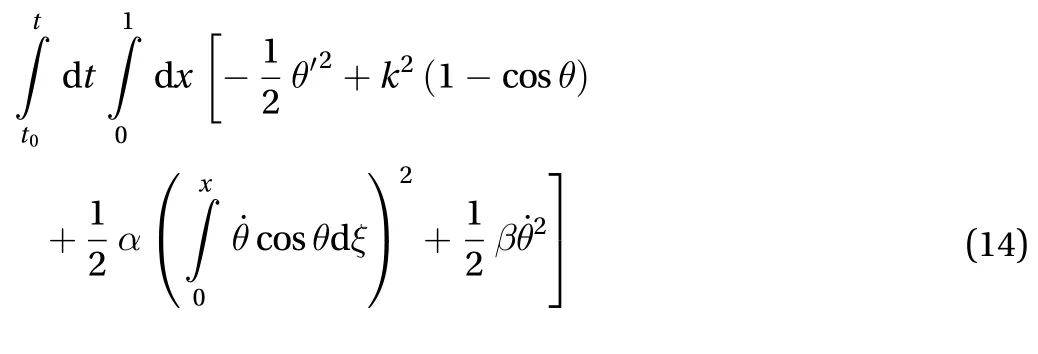
the minimum, where integrand with respect to timeis the Lagrange function of the column. Variation of the first order for functional is

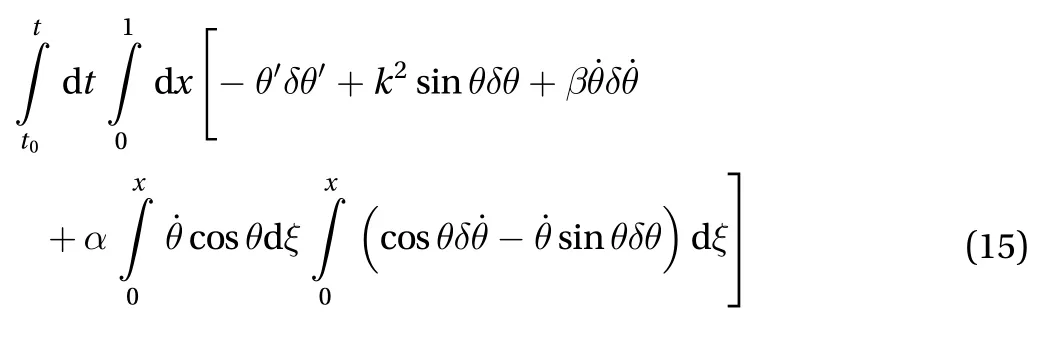
Because variation vanishes when θ (x，t)≡ 0, we know thatis the null solution or an equilibrium point. Whenand0, i.e., the column in straight shape is an equilibrium,the total energy Eq. (11) of the system vanishes.θ

Because the tangential angle is infinitesimal in the infinitesimal-amplitude vibration, we have the approximationsfrom which,dimensionless form of the total energy in Eq. (11) reduces to

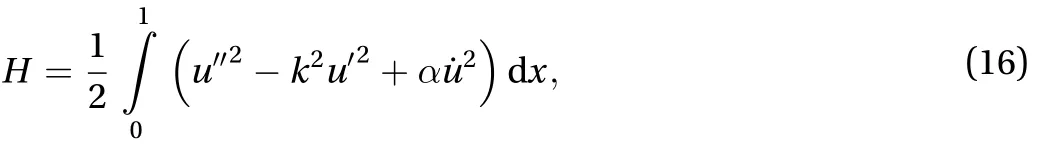
whereis dimensionless form of the deflection, andBoundary conditions are

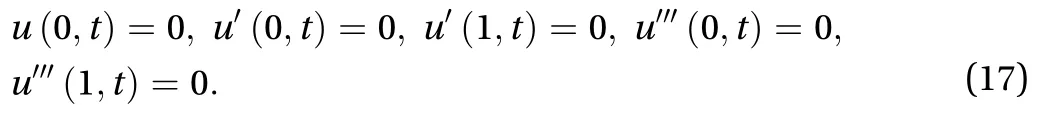
Considering conditions in Eq. (17), we have the Fourier series of dimensionless form of deflection

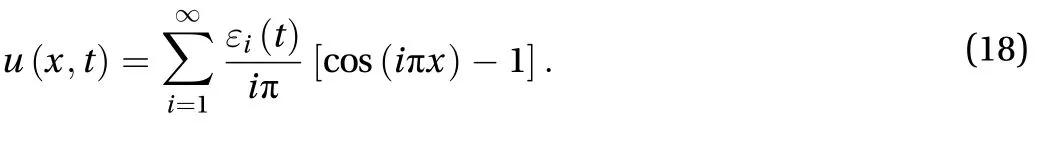
Similarly, when, i.e., the column in straight shape is an equilibrium, the total energy in Eq. (16) of the system vanishes. The total energy Eq. (11) is available for the finiteamplitude vibration, while the total energy Eq. (16) is available for the infinitesimal-amplitude vibration.

3 Dynamic stability of the column when ∈ (0, π]

Consider a-degree-of-freedom conservative system with the state variables in Eq. (1). The total energy of the system is

whereis potential energy,

whereis a parameter, m =3，4，5，···，

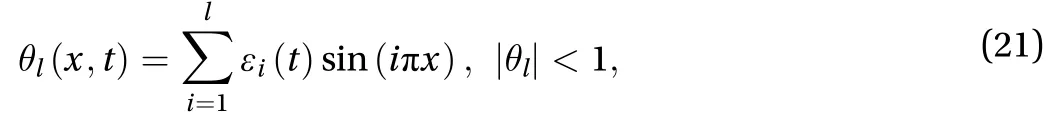
andis kinetic energy,

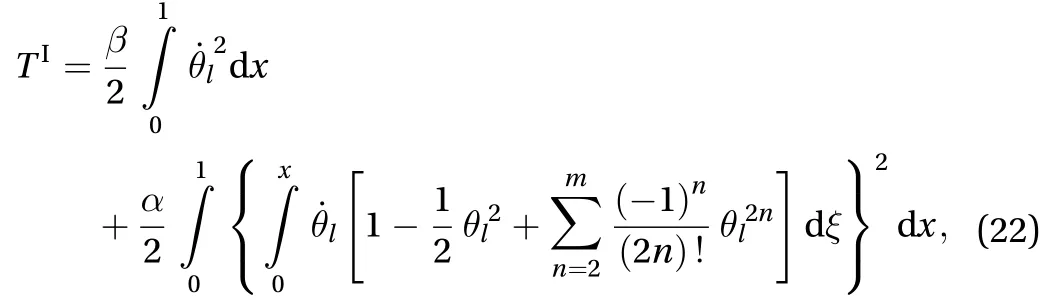
where,are positive constants,At boundary, we have

The-degree-of-freedom conservative system defined by Eqs.(19)-(23) with a parameteris called system I. Substituting Eq. (21) into Eqs. (20) and (22), then into Eq. (19), we have the total energy of system I

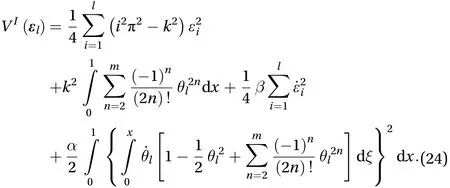
For the-degree-of-freedom conservative system, the total energy Eq. (24) is a Lyapunov function. Based on the Hamilton principle, trajectory of the system makes functional

the minimum, where integrand is the Lagrange function of system I. Substituting Eqs. (20), (22) into Eq. (25), we have variation of the first order for functional Eq. (25)

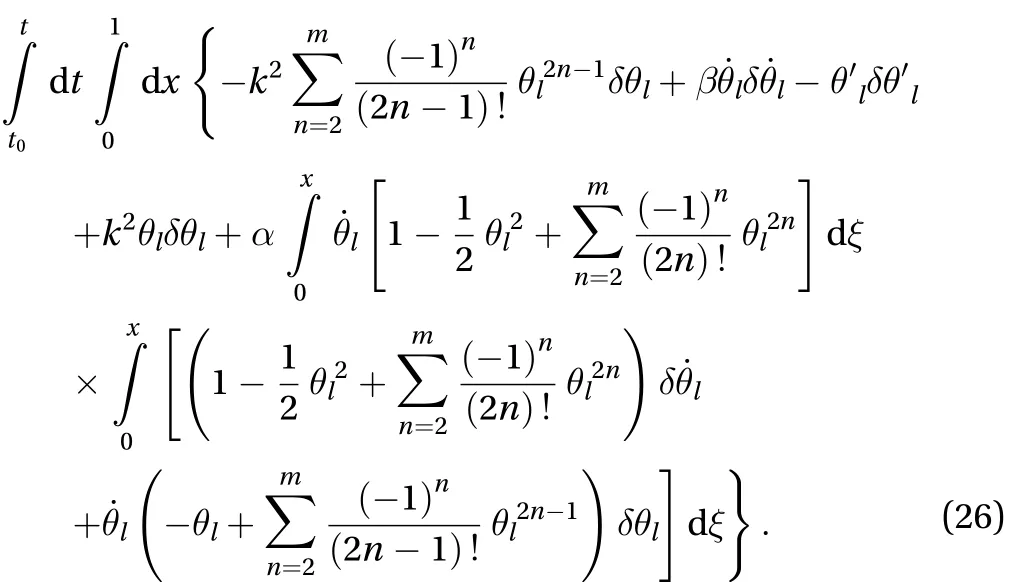
Because the variation Eq. (26) vanishes when, we know thatis the null solution or an equilibri-um point.

Becausewe know that the second term in the righthand side of Eq. (24), i.e.is positive-definite with respect to. The third term in the right-hand side of Eq. (24),is positive-definite with respect toThe fourth term in the right-hand side of Eq.(24), i.e.is non-negative and vanishes whenThereforein Eq. (22) is positive-definite with respect toi.e., the kinetic energy of the system is identically positive-definite with respect to general velocity. Positive definiteness ofin Eq. (24) is dependent on positive definiteness of the first term in the right-hand side of Eq. (24), i.e.

Because the system is conservative, the total energyin Eq.(19) is a constant along every trajectory. We know that the total time derivativevanishes along every trajectory of the system. Therefore,is negative semi-definite along every trajectory of the system, i.e., one of the conditions in the Lyapunov stability theorem before is satisfied.

3.1 Dynamic stability of the -degree-of-freedom system when the parameterk∈ (0，)

When k ∈ (0，), the first term in the right-hand side of Eq.(24), i.e.is a positive-definite quadratic form ofWe know that the Lyapunov function in Eq. (19)is positive-definite with respect to. Therefore if and only if, the Lyapunov function VI(l)=0; otherwise the Lyapunov function VI(l)＞0 whenl/=0. VI(l) is a positive-definite function with respect to. By the Lyapunov stability theorem,we know that the-degree-of-freedom system is dynamically stable in the sense of Lyapunov when k ∈ (0，).

3.2 Dynamic stability of the -degree-of-freedom system for when the parameter k=π

When, the first term in the right-hand side of Eq. (24),is a positive semi-definite quadratic form ofIn fact, except fori=0(i=1，2，3，···，l), if and only ifthe first term in the right-hand side of Eq. (24) vanishes. Because the second term in the right-hand side of Eq. (24) is positive-definite with respect tothe second term in the right-hand side of Eq.(24) is positive when1/=0，i=0(i=2，3，4，···，l). Therefore sum of the first and the second term in the right-hand side of Eq.(24) is positive-definite with respect to1，2，3，···，l. Becausein Eq. (22) is positive-definite with respect tothe Lyapunov function in Eq. (19) is positive-definite with respect to. Based on the Lyapunov stability theorem, we conclude that the-degree-of-freedom system is dynamically stable in the sense of Lyapunov when.

Finally the formulation in subsections 3.1 and 3.2 is available forand. Weconclude thatthe systemI is stable forandwhenWhenand

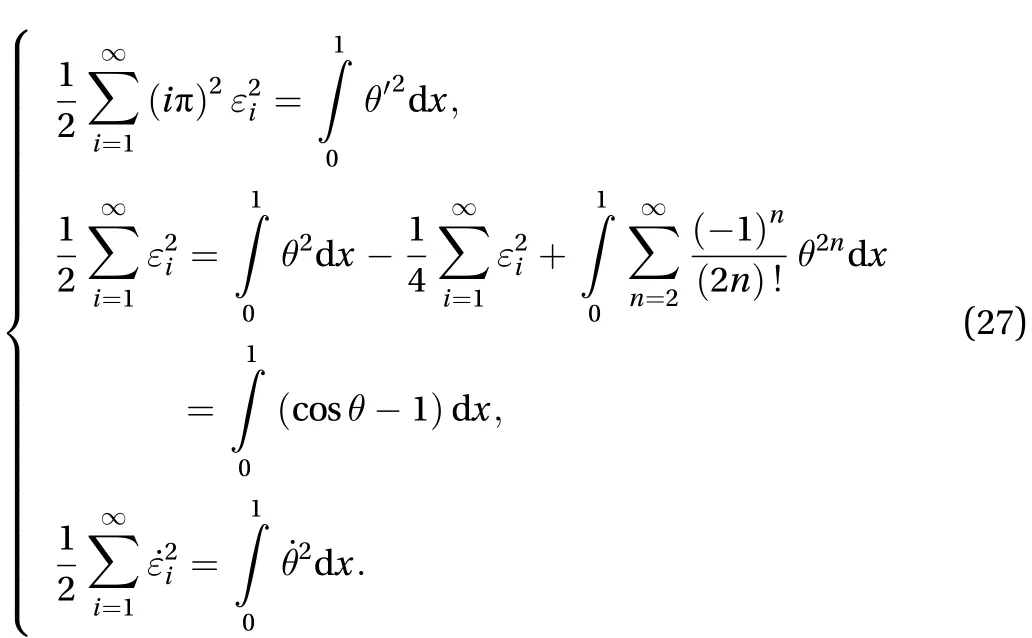
Substituting Eq. (27) into the total energy of the system I in Eq. (24), we have the dimensionless form of the total energy Eq.(11) of the column in Fig. 1, in vibration, where,, andhave the significance in Eqs. (8)-(10). Boundary conditions in Eq. (23)reduce to boundary conditions in Eq. (12) of the column. The system I comes to the column in Fig. 1. Substituting the second and the fourth equation in Eq. (27) into the Euclidean norm in(2), we have

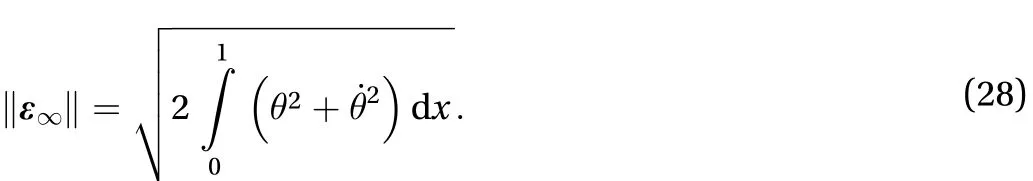
Therefore, we come to the conclusion that the column is dynamically stable in the sense of Lyapunov when the load is smaller than or equal to the Euler critical load, i.e. k ∈ (0，], which is identical with the conclusion of Movchan [19].

4 Instability of the column whenk∈(，∞)

Consider another-degree-of-freedom conservative system with the state variables in Eq. (1). Total energy of the system is

whereis the potential energy of the system,

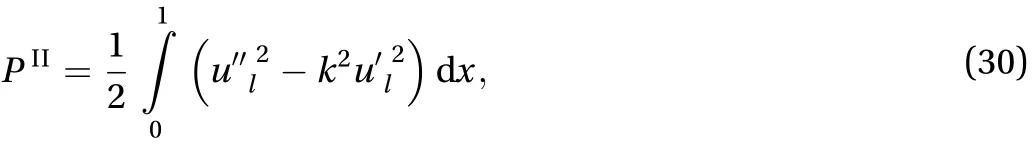
is kinetic energy of the system,

whereis a parameter,is a positive constant, and

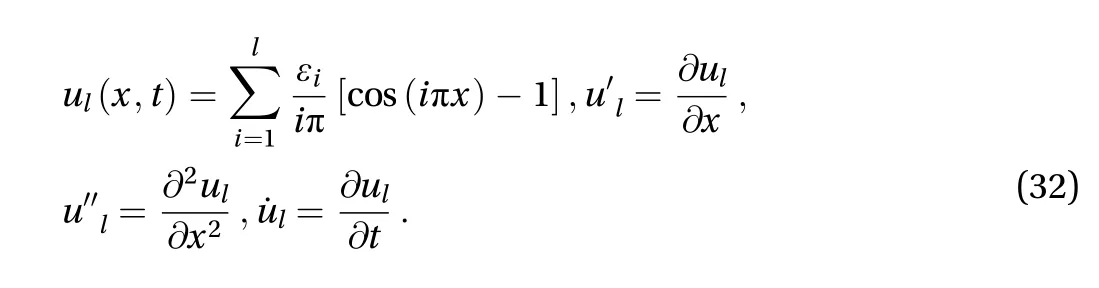
Substituting Eq. (31) into Eqs. (30), (32), then into Eq.(29), we have the total energy

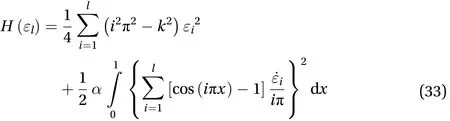
The-degree-of-freedom conservative system with the parameterdefined by Eqs. (29)-(33) is called system II. At boundary, we have

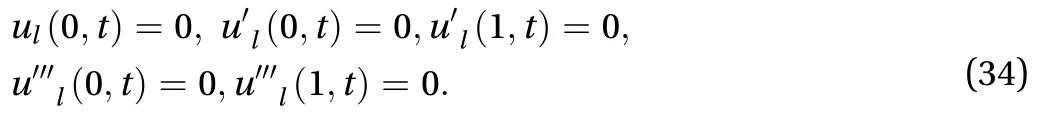
Based on the Hamilton principle, trajectory of the system makes functional

the minimum where integrand is the Lagrange function of system II. Substituting Eqs. (30), (32) into Eq. (35), we have variation of the first order for functional (35)

Because the variation (36) vanishes when ul(x，t)≡ 0, we know that ul≡0, i.e., is the null solution or an equilibrium point.

For a trajectory of the system, variation of the first order vanishes for arbitrary. Substituting Eq. (31) into Eq. (36) and considering independence of δ1，δ2，δ3，···，δl, we have

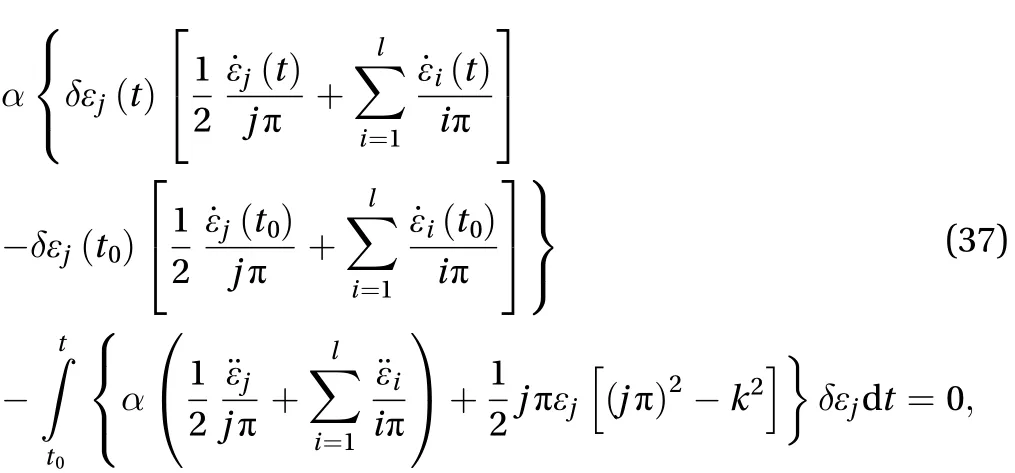
where j =1，2，3，···，l. Because Eq. (37) stands for arbitrary, we have

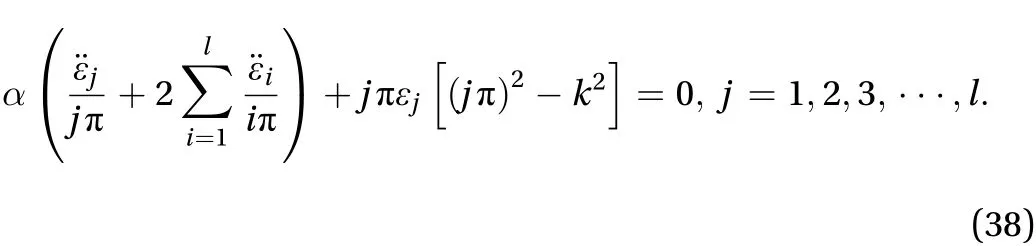
Letin Eq. (38), we have

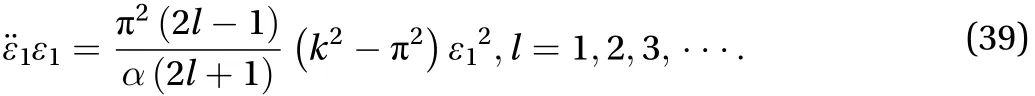
When l → ∞, Eq. (39) comes to

In Eqs. (39), (40), we have

when.

When, the first term on the right-hand side of Eq.(33) is indefinite with respect to1，2，3，···，l. In the phase space,the first term on the right-hand side of Eq.(33) has no minimum in the neighborhood of the origin. The second term on the right-hand side of Eq.(33) is a quadratic form with respect to

We consider another Lyapunov function in the form

Because

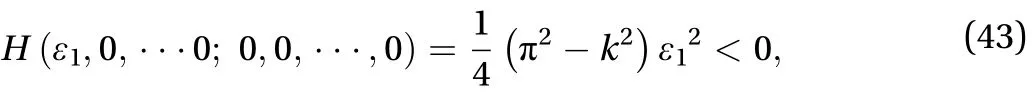
when k＞ ，there must exit sufficiently smallso that

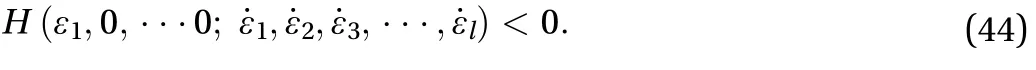
In addition to, we havewill be designated byin the phase space

Hencein, and moreover,on the boundaries ofbecause eitheroron these boundaries. It is also obvious that the origin in the phase space is a point on the boundary.

The total time derivative of the Lyapunov function in Eq.(42)is

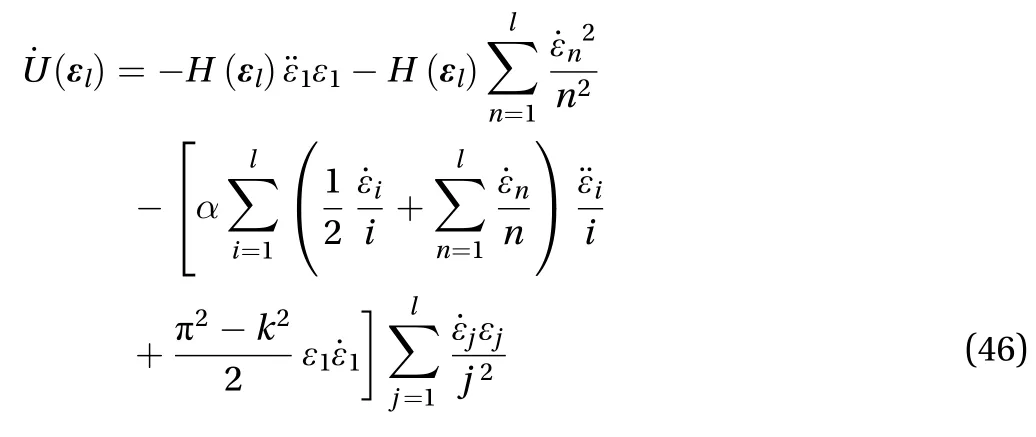
whereandBecause the second and the third term on the right-hand side of Eq. (46) are higher order terms with respect to the sufficiently smallsignof is determined by the first term on the right-hand side of Eq.(46), i.e. - H. From inequalities Eqs. (41) and (44), we know that -＞0, i.e., the first term on the right-hand side of Eq. (46) is positive. The total time derivative of the Lyapunov function in Eq. (46) is positive-definite along every trajectory of the system, i.e.

By the Lyapunov instability theorem, we conclude that the system II is dynamically unstable in the sense of Lyapunov when k∈(，∞).

In addition, because inequality Eq. (41) stands when l → ∞,we conclude that the system II is dynamically unstable in the sense of Lyapunov for l → ∞ when k ∈(，∞).

When l → ∞, letting u∞=u in Eqs. (30)-(32) and comparing with Eq.(18), we have

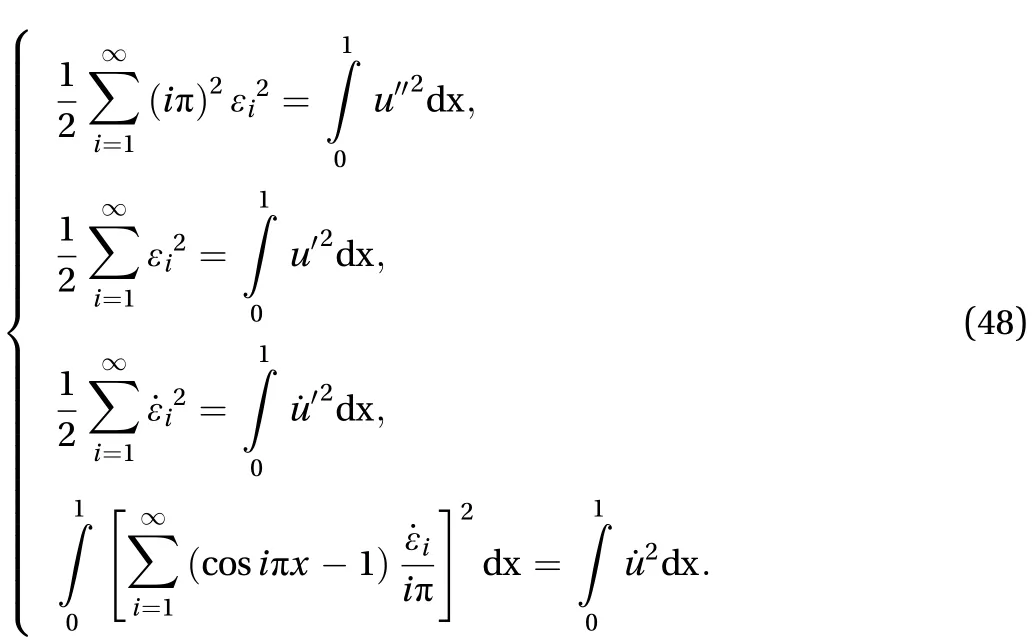
Substituting Eq.(48) into total the energy of the system II in Eq. (29), we have the dimensionless form of the total energy Eq.(16) of the column in Fig.1 In the small-amplitude vibration,whereandare the load factor and the inertia term in Eq.(16), respectively. Boundary conditions in (34) reduce to boundary conditions in Eq. (17) of the column. Substituting the second and the third equation in Eq.(48) into the Euclidean norm in Eq.(2), we have

Therefore, we conclude that the column is dynamically unstable in the sense of Lyapunov when the load is greater than the Euler critical load.

5 Conclusions

By the Lyapunov stability and instability theorems, the system I is proved to be dynamically stable when the parameter k∈ (0，], while the system II is proved to be dynamically unstable when the parameter k ∈(，∞). When the number of degree of freedom tends to infinite, the two systems come to the column with one end fixed and the other clamped in rotation.We come to the conclusion that the column is dynamically stable in the sense of Lyapunov when the load is smaller than or equal to the Euler critical load, while dynamically unstable in the sense of Lyapunov when the load is greater the Euler critical load. However analysis of dynamic stability of columns with other boundary conditions, such as simply supported conditions,remains open.

Acknowledgement

The project was supported by the Research Fund for the Doctoral Program of Higher Education of China (20120009110019).

References

[1]S. Woinowsky-Krieger, The effect of an axial force on the vibration of hinged bars, J. Appl. Mech. 17 (1950) 35–36.

[2]J.E. Brown, J.M. Hutt, A.E. Salama, Finite element solution to dynamic stability of bars, AIAA J. 6 (1968) 1423–1425.

[3]R.W. Dickey, Free vibrations and dynamic buckling of the extensible beam, J. Math. Anal. Appl. 29 (1970) 443–454.

[4]E.L. Reiss, B.J. Matkowsky, Nonlinear dynamic buckling of a compressed elastic column, Quart. Appl. Math. 29 (1971)245–260.

[5]W.Y. Tseng, J. Dugundji, Nonlinear vibrations of a buckled beam under harmonic excitation, J. Appl. Mech. 38 (1971)467–476.

[6]J.M. Ball, Initial-boundary value problems for an extensible beam, J. Math. Anal. Appl. 42 (1973) 61–90.

[7]A.M. Abou-Rayan, A.H. Nayfeh, D.T. Mook, Nonlinear response of a parametrically excited buckled beam, Nonlinear Dyn. 4 (1993) 499–525.

[8]A.A. Afaneh, Nonlinear response of an initially buckled beam with,1:1 internal resonance to sinusoidal excitation, Nonlinear Dyn. 4 (1993) 547–571.

[9]A.H. Nayfeh, W. Kreider, T.J. Anderson, Investigation of natural frequencies and mode shapesof buckled beams, AIAA Journal 33 (1995) 1121–1126.

[10]C.M. Chin, A.H. Nayfeh, Three-to-one internal resonances in hinged-clamped beams, Nonlinear Dyn. 12 (1997) 129–154.

[11]W. Kreider, A.H. Nayfeh, Experimental investigation of singlemode responses in a fixed–fixed buckled beam, Nonlinear Dyn.15 (1998) 155–177.

[12]S.A. Emam, A.H. Nayfeh, On the nonlinear dynamics of a buckled beam subjected to a primary-resonance excitation,Nonlinear Dyn. 35 (2004) 1–17.

[13]S.A. Emam, A.H. Nayfeh, Nonlinear responses of buckled beams to subhar- monic-resonance excitations, Nonlinear Dyn.35 (2004) 105–122.

[14]A.H. Nayfeh, S.A. Emam, Exact solution and stability of postbuckling configurations of beams, Nonlinear Dyn. 54 (2008)395–408.

[15]A. Mamandi, M.H. Kargarnovin, S. Farsi , Dynamic analysis of a simply supported beam resting on a nonlinear elastic foundation under compressive axial load using nonlinear normal modes techniques under three-to-one internal resonance condition, Nonlinear Dyn. 70 (2012) 1147–1172.

[16]X.D. Yang, W. Zhang, Nonlinear dynamics of axially moving beam with coupled longitudinal–transversal vibrations, Nonlinear Dyn. 78 (2014) 2547–2556.

[17]S.A. Emam, M.M. Abdalla, Subharmonic parametric resonance of simply supported buckled beams, Nonlinear Dyn. 79 (2015)1443–1456.

[18]M.H. Ghayesh, H.Farokhi, Parametric instability of microbeams in supercritical regime, Nonlinear Dyn. 83 (2016)1171–1183.

[19]A.A. Movchan, The direct method of Liaponuv in stability problems of elastic systems, J. Appl. Math. Mech. 23 (1959) 686–700.

[20]H.G. Zhang, Z.S. Wang, D.R. Liu, Robust stability analysis for interval Cohen–Grossberg neural networks with unknown timevarying delays, IEEE Transactions On Neural Networks 19(2008) 1942–1955.

[21]K.B. Shi, X.Z. Liu, Y.Y. Tang, et al., Some novel approaches on state estimation of delayed neural networks, Information Sciences 372 (2016) 313–331.

[22]K.B. Shi, Y.Y. Tang, X.Z. Liu, et al., Non-fragile sampled-data robust synchronization of uncertain delayed chaotic Lurie systems with randomly occuring controller gain fluctuation, ISA Transactions 66 (2017) 185–199.

[23]L. Meirovitch, Methods of Analytical Dynamics. McGraw-Hill Book Company, New York (1970)