Forced vibration analysis of nano-composite rotating pressurized microbeam reinforced by CNTs based on MCST with temperature-variable material properties

R. Rostmi , M. Mohmmdimehr,*, M. Ghnnd A. Jlli

a Department of Solid Mechanics, Faculty of Mechanical Engineering, Shahrood University of Technology, Shahrood, Iran

b Department of Solid Mechanics, Faculty of Mechanical Engineering, University of Kashan, Kashan, Iran

1 Introduction

Nanotechnology is employed to produce new materials such as tools, systems, andgenerators for controlling the manufacturing processes in atomic and molecular dimensions. The carbon nanotubes (CNTs) were discovered by Iijima [1] in 1991 and more researches have been published in the literature aboutvibration, buckling and wave propagation of micro/nanobeam.These materials have many applications in micro/nano electromechanical systems (MEMS/NEMS), sensors, actuators, and fluid storage [2]. Several researchers have been studied the stability of micro/nano structures under magneto-electro-thermomechanical loadings. Wang [3] studied vibrations of micro-tube containing the fluid flow by using the Euler–Bernoulli beam theory and employed the modified couple stress theory (MCST). His results showed that by increasing the velocity of fluid flow, the natural frequency decreases. Using the first order shear deformation theory (FSDT), Ghannad et al. [4] analyzed thick-walled cylindrical truncated cone. Their results showed that the axial and radial displacements and radial stress are very dependent on the angle of the cone-shaped cylinder. Based on the nonlinear von Kármán assumption, Xue et al. [5] presented the nonlinear vibration orthotropic plate. Their numerical results indicated the effect of the magnetic field, the thickness and material properties on natural frequency. Bayat et al. [6] illustrated thickwalled sphere made of functional graded material (FGM) under thermal and mechanical fields. From their results can be found that the power index of FGM has great influence on the design of the geometry of the sphere. Ghorbanpour Arani et al. [7] studied the volume fraction effect of CNTs on magnetic, electrical,thermal, and mechanical properties of smart nano-composite cylinder. It can be seen from the results that the effect of inside pressure on the radial stress is more than magnetic, electrical,and temperature loadings. Using the third order shear deformation theory (TSDT) and employing the principle of minimum potential energy, Ghannad and Gharooni [8] investigated the mechanical behavior of FGMs cylinder. The results showed that the use of FGM with the lower power index reduces the residual stress and displacement in the cylinder. Kim and Reddy [9] analyzed the bending, buckling, and vibration analysis of FGM plate using the Navier’s type solution. Their study showed that with increasing the power index of FGM, critical buckling load and natural frequency reduces. Lopatin and Morozov [10] examined the buckling analysis of composite cylinder using Galerkin method. They investigated the effect of geometric parameters and material properties on the critical buckling load. The results of their work are compared with the finite element method(FEM). Shen and Xiang [11] investigated post buckling cylindrical nano-composite reinforced with CNTs under axial and radial pressures in thermal field. The results of their work showed that the critical buckling load decreases with increasing temperature changes. Ghannad and Gharooni [12] obtained the displacement and stress of FGM cylinder under pressure and rotating loadings using FSDT. Zhang and Li [13] studied the buckling and vibration of FGM magneto-electro-thermo-elastic circular cylindrical shells using TSDT. They obtained equilibrium equations of FGM magneto-electro-thermo-elastic circular cylindrical shells based on the Hamilton’s principle and then computed these equations. From the results can be seen that with increasing magnetic and electrical fields, the natural frequency and critical buckling load increases. Mohammadimehr and Rahmati[14] studied the effect of small scale parameter on the vibration of single-walled boron nitride nanorods (SWBNNRs) using magnetic fields and mechanical loading. Their results showed that with an increase in nonlocal parameter decreases the natural frequency of SWBNNRs, also with increasing temperature change, the amount of displacement increases. Alshorbagy [15]presented the effect of material-temperature dependent on the vibrational characteristics of a functionally graded (FG) thick beam by using finite element method. His results showed that the former mentioned effects play a very important role on the dynamic behavior of thick FG beams. Li et al. [16] used nonlocal theory to analyze the buckling and vibration of nano-plate under magnetic and electrical fields. It is seen that by increasing the lateral force and small scale parameter, the critical buckling load and natural frequency decreases. Rahmani and Pedram[17] investigated the size effect on vibration of the FG nanobeam by using nonlocal Timoshenko beam theory. Their results indicated that the power index of FGM has a prominent role in system response. Zhang et al. [18] used Ritz method to analyze vibration triangular nano-composite plate reinforced by CNTs.Their results showed that the natural frequency increases with increasing volume fraction of CNTs. Rahmati and Mohammadimehr [19] examined vibrations of boron nitride nanorod using differential quadrature method (DQM). Their results can be used for design and control of micro- and nano-scale tools.Sofiyev and Kuruoglu [20] employed the buckling and vibration analysis of FGM cylindrical shell under external pressure. Using higher-order shear theory, they obtained the equilibrium equations and solved these equations using Galerkin method. Their research showed that with increasing length to radius ratio, the critical buckling load decreases. Shen and Xiang [21] studied the nonlinear vibration of nano-composite cylindrical shell under thermal field on elastic foundation. From their results can be concluded that the natural frequency decreases with increasing temperature change, while the linear to nonlinear frequency ratio increases. Using TSDT, Nami et al. [22] illustrated nonlocal thermal buckling and vibration of FGF nano-plate. They investigated the effect of the nonlocal parameters on the natural frequency. Ansari et al. [23] used strain gradient theory for analysis bending, buckling and vibration of FG micro-plate. By applying this theory and employing Hamilton's principle, the equations of motion are obtained. Also, they investigated the effect of thickness on the critical load and the natural frequency of system.Mohammadimehr et al. [24] used modify couple stress theory for buckling and vibration analysis of double-bonded nano-composite piezoelectric plate reinforced by boron nitride nanotube.Their results showed that the natural frequency and critical buckling load increase with increasing material length scale parameter. Du et al. [25] employed the nonlinear forced vibration analysis of FGM cylindrical shell. The effect of power-law exponent on the amplitude response of the system is discussed.Ma et al. [26] presented free and forced vibration analysis of coupled conical-cylindrical shells with arbitrary boundary conditions using a modified Fourier–Ritz method. Numerical examples are conducted to illustrate the forced vibration behavior of the coupled conical-cylindrical shell subjected to the excitation forces in different directions. Ghorbanpour Arani et al. [27]analyzed the vibration of double visco-elastic CNTs conveying viscous fluid coupled by visco-Pasternak medium based on nonlocal theory. The results of this research could be used in design and manufacturing of nano/micro mechanical system in advanced biomechanics applications with magnetic field as a parametric controller. Ke and Wang [28] investigated the free vibration of magneto-electro-elastic (MEE) nano-beams based on the nonlocal theory and Timoshenko beam theory. They derived governing equations and boundary conditions by using the Hamilton’s principle and discretized by using the differential quadrature (DQ) method to determine the natural frequencies and mode shapes. Their results showed influence of the nonlocal parameter, temperature rise, external electric, and magnetic potentials on the size-dependent vibration characteristics of MEE nanobeams. Beni et al. [29] studied free vibration of sizedependent shear deformable FG cylindrical shell based on MCST. The obtained results through the MCST are shown the considerable effect of the size dependent parameter, particularly in more thickness and shorter length of nanotubes, on the natural frequency. Ansari et al. [30] illustrated forced vibration behavior of composite plates reinforced by CNTs. Their results showed that with an increase in the CNT volume fraction, the flexural stiffness of plate increases; and hence its natural frequency gets larger. Nejad et al. [31] studied functionally graded rotating thick hollow cylinder with variable thickness and clamped ends, semianalytically under arbitrarily non-uniform pressure on the inner surface. Their obtained results of the disk form multi-layers method (MLM) are compared with those of FEM. Lü et al. [32]examined forced vibration of two coupled CNTs under moving nano-particles. Their results indicated that, because of the lag,the maximum transverse deflections of both coupled tubes can be reduced. Salehipour et al. [33] presented free vibration functionally graded micro/nano plates based on modified couple stress and three-dimensional elasticity theories. The equations of motion and boundary conditions are derived using Hamilton's principle. Analytical closed-form solutions are presented for both in-plane and out-of-plane free vibrations of simply supported plates. Their results showed the effects of material length scale parameter and material gradient index on the natural frequencies for FG micro/nano plates. Ziaee [34] investigated linear free vibration of buckled FG nano-beams. The author derived the partial differential equation of motion based on Euler–Bernoulli beam theory, von Kármángeometric nonlinearity and Eringen’s nonlocal elasticity theory. The results showed the important role of compressive axial force exerted on FG nanobeams in nonlocal behavior of vibrating FG nano-beams.Ghorbanpour Arani and Zarei [35] illustrated the vibration and stability of a Y-shaped single-walled carbon nanotube (SWCNT)embedded in visco-pasternak foundation and conveying nanomagnetic viscous fluid (NMF) based on nonlocal elasticity theory and Euler–Bernoulli beam model. Their results indicated that increasing the angle between centerline of CNT and the downstream elbows decreases stability of system. Arani and Maraghi [36] studied the vibrational behavior of magnetostrictive plate as a smart component. They derived equations of motion by using Hamilton’s principle and solved the equations by DQM considering general boundary conditions. It can be seen from the results that magneto-mechanical coupling in magnetostrictive plate helps to control vibrational behaviors of systems such as electro-hydraulic actuator, wireless linear motors and sensors.

In this article, free and forced vibration analysis of nanocomposite rotating pressurized microbeam reinforced by CNTs subjected to magnetic field based on MCST with temperaturevariable material properties is investigated. The magnetic field is inserted in the thickness direction of the nano-composite microbeam. The governing equations are obtained based on the Hamilton’s principle and then computed these equations by using Navier’s solution. The results show the effect of various parameters such as angular velocity, temperature changes, and pressure between of the inside and outside, the magnetic field, material length scale parameter, and volume fraction of nano-composite microbeam on the natural frequency and response system and also effects shock of change the external force in different period of time on response system for nano-composite microbeam based on modified couple stress theory is novelty of the present paper. Manufacturing sensors, displacement fluid, and drug delivery is the practical aspect of this research.

2 The equation of motion fornano-composite microbeam

It is assumed that micro-tube with an angular velocityis spinning around its axis. In Fig. 1, the inside and outside temperature of the cylinder are Ts1and Ts2, respectively. Also, Piand Poare the inside and outside pressure, respectively. The magnetic field is applied in length direction of micro-tubes. ri, ro, h, and L denote inside radius, outside radius, thickness, and length, respectively.

According to the Euler–Bernoulli beam theory, the displacement components can be written as follows:

where u and w are the displacement components in the x- and zdirections, respectively. Strain tensor components are calculated by using the following relations:

Based on the modified couple stress theory, the components of the symmetric curvature tensor () are defined as the following form:

whereis the components of the rotation vector that can be expressed as follows:

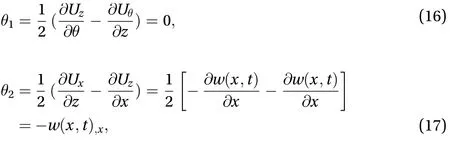
By substituting Eqs. (16)–(18) into Eqs. (10)–(15), the components of the symmetric curvature tensorare obtained as follows:

Substituting Eqs. (19)–(24) into Eqs. (25)–(30), the components of the couple stress tensor are considered as follows:

where l is the material length scale parameter,denotes the shear modulus. The governing equations of motion for nanocomposite micro-tube are derived using the Hamilton’s principle which is given by:

where,, andare the variations of kinetic energy, strain energy, the work done by external applied forces, respectively.Variations of the kinetic energy for sandwich plate can be described as follows:

where

According to the modified couple stress theory, the variation form of strain energy is expressed as follows:

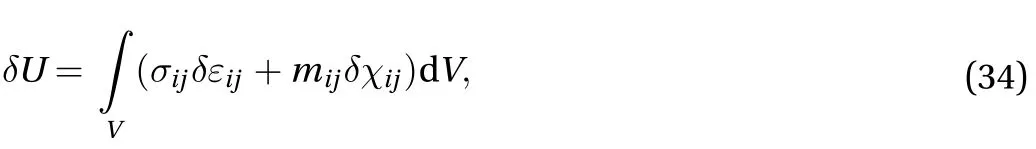
whereandare the components of stress and strain tensors,respectively. mijis couple stress tensor.

where R is the average radius of microbeam.

The linear constitutive relations for orthotropic nano-composite microbeam in cylindrical coordinates can be written as:

whereis the stiffness components of the orthotropic microbeam. Additionally,anddenote the coefficient of thermal expansion and temperature changes, respectively.

where,,, andare Young's modulus and Poisson's ratio, respectively. These are calculated using mixture rule.where,, andare Young’s moduli of CNT and the matrix, respectively.andare volume fraction of CNT and the matrix, respectively.is the Poisson's ratio of microbeam.

Alsoandare coefficient of thermal expansion in the longitudinal and radial direction.

Substituting Eq. (36) into Eq. (35) yields:

wheredenote the resultant forces and moments, respectively.is the transverse shear forces which are all defined by the following expressions:

The electro-dynamic Maxwell's equations for the nano-composite microbeam can be written as follows:

where U, H, andare the displacement fields (u, v, w), the magnetic field, and the magnetic permeability, respectively. If the magnetic field (0, 0, Hx) is applied in length of the nanocomposite micro-tube, Lorentz forces using Eqs. (50)–(52) are obtained as follows:

Then variation of the work done by the Lorentz forces is calculated as:

Variation of the external work by the body force and the surface force as follows:

By using Eqs. (32), (46), (56)–(58), the equilibrium equations of nano-composite microbeam can be obtained as the following form:

Substituting Eqs. (47)–(49) into Eqs. (59), (60) yields:

3 The Navier’s type solution for nano-composite rotating pressurized microbeam

Assuming that the boundary conditions are simply supported in both ends of nano-composite rotating pressurized microbeam reinforced by CNTs, Navier's type solution can be used to solve the equations ofmotion as follows:

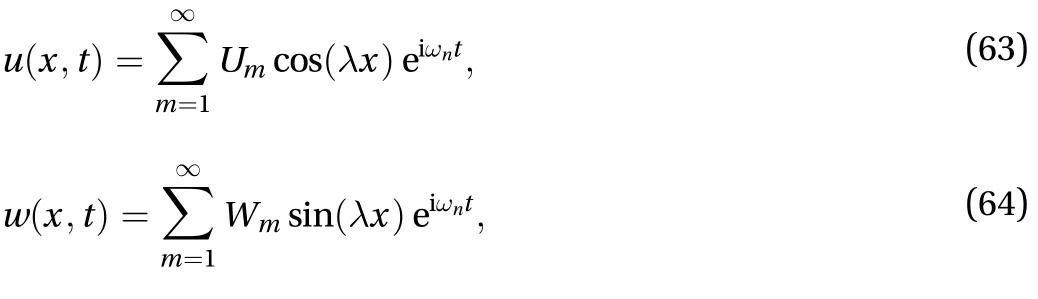
whereis equal to.

Substituting Eqs. (63), (64) into Eqs. (61), (62), the matrix form for the motion equations of nano-composite micro-tube can be expressed as follows:

where

To obtain the natural frequency, the determinant of coefficient matrix in Eq. (62) should be equal to zero:

To investigate the effect of different parameters such as outside to inside pressure and temperature, the magnetic field, angular velocity and volume fraction of CNTs on response system,consider total external work on the microbeam F (t). The work done on microbeam is a function of time that is defined as follows:

The work done using the Fourier series is expressed as follows

where

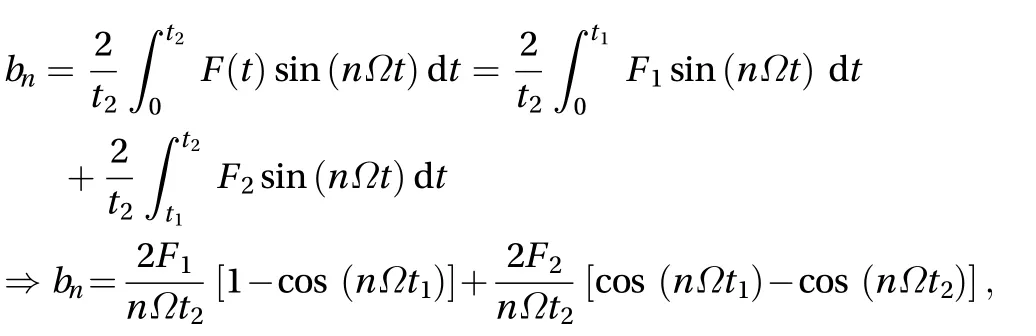
whereis the excitation frequency of the system, which is directly related to t1and t2times in Eq. (66). It can be seen that the excitation system depends to during times change of pressure, the timing of these changes is shorter, the excitation frequency will increase. Matrix form response system to microtube as follows:

In this study pressure parameter at different period of time,have a different value. These parameter at each period of time definition are in Table 1.

Table 1 Parameters at each period of time.

4 Numerical results and discussions

In this article, free and forced vibration analysis of nanocomposite rotating pressurized microbeam reinforced by CNTs subjected to magnetic field based on MCST with temperaturevariable material properties is studied. The effects of various parameters such as angular velocity, temperature changes, and pressure between of the inside and outside, the magnetic field,material length scale parameter, and volume fraction of nanocomposite microbeam on the natural frequency and response systemare investigated. The used material in the matrix is polymethylmethacrylate (PMMA). The mechanical properties of PMMA areas a function of ambient temperature. The following equation shows the mechanical properties of matrixthat are temperature-dependence [13].

where T0andare room temperature and temperature change, respectively. In Tables 2 and 3 are presented the mechanical properties depend on the temperature and volume fraction of nanotubes, respectively [13].

Table 2 Temperature-dependent material properties for SWCNT.

Table 3 The efficiency parameters of CNT dependent to different volume fraction.

In order to check the reliability and accuracy of the model,comparing the results of the previous study was conducted by present study. Data taken to calculate the natural frequency of the CNTs are as follows:

From Fig. 2, we can see that Euler–Bernoulli beam model provided for long and thin-walled microbeam has little difference with the thin cylindrical thin shell model, but for short and thick-walled cylinder model was not reliable. Dimensionless natural frequency and deflectionare defined as follows:

Fig. 1. Schematic view of a nano-composite micro-tube.

Fig. 2. Comparison between the present work and Zeighampour and Beni [37] for dimensionless natural frequencyhomogeneous CNT with simply support boundary conditions.

Fig. 3. Effect of magnetic field on the dimensionless natural frequency (Vcnt = 0.12, T = 300 K, R/h = 50, l/h = 25, m = 1).

The effects of various parameters on the dimensionless natural frequencies of microbeam reinforced by CNT are studied.Figure 3 shows the influences of magnetic field on the natural frequency. It is seen that with an increase in magnetic field, the stiffness of system decreases so that the natural frequency decreases. Based on nonlocal theory (NT), Fig. 4 depicts the effect of volume faction of CNTs on the dimensionless natural frequency of microbeam. In this graph, it can see that with increasing volume fraction of CNTs, the dimensionless natural frequency increases. On the other hands, the stiffness of the system increases with increasing volume fraction. Also in the different of L/R the deference value between 0.17 and 0.28 volume fraction of CNT is approximately the same. Figure 5 shows the effects of temperature change on dimensionless natural frequency. From this figure, it can be found that increasing temperature change,the stiffness of nano-composite microbeam decreases because the elasticity module of resin and matrix and molecular force between resin and matrix decreases so that the dimensionless natural frequency decreases. In Fig. 6, the influence of material length scale parameter on dimensionless natural frequency is presented. With increasing this parameter, the dimensionless natural frequency of microbeam increases for L/R ＜ 20. Also it can be seen more influence of material length scale parameter in L/R ＜ 20. It is seen that with an enhance in the material length scale parameter, the stiffness of microbeam increases and this point leads to rise the dimensionless natural frequency.

Fig. 4. Effect of volume fraction of CNT on the dimensionless natural frequency (R/h = 50, T = 300 K, Hx = 0, l/h = 25, m = 1).

Fig. 5. Effect of temperature on the dimensionless natural frequency (Vcnt = 0.12, R/h = 50, Hx = 0, l/h = 25, m = 1).

The influences of different parameter on dimensionless response system are presented in Figs. 7-16. Figure 7 shows the effect of volume fraction of CNT on dimensionless response of microbeam. By increasing the volume fraction of CNTs, natural frequency increases and this figure excitation frequency of a relationship with natural frequency but with increasing volume fraction of carbon nanotube the system is stiffer, so that the amplitude of response of system will not significant change. Figure 8 indicates the effect of inside to outside pressure on dimensionless response of microbeam. By increasing the inside to outside pressure the amplitude of the system increases. By increasing the deference pressure between inside and outside can be caused the increasing of external force. So that with passing of time the amplitude of microbeams increases. Figure 9 presents influences the temperature on dimensionless response of microbeam. By increasing the temperature the stiffness of system decreases, also the excitation frequency decreases. With considering two parameters, the amplitude of the system decreases.Figure 10 shows the effect of angular velocity on the amplitude of the system. With increasing angular velocity the natural frequency decreases, so that the excitation frequency decreases.This diminution of excitation frequency caused the decrease of amplitude of the microbeam. Figure 11 depicts the effect of magnetic field on the dimensionless response system to. With increasing magnetic field the amplitude of system decreases because the excitation frequency and stiffness of system decreases.So that one of the best methods to control of the microbeam system and increasing the stability of this system is applied the magnetic field. Figure 12 shows the effect of volume fraction of CNT on the dimensionless response system to. With increasing volume fraction of CNT, maximum amplitude system decreases. By increasing the volume fraction of CNT the stiffness of system increases, also the excitation frequency decreases. With considering two parameters, the amplitude of the system decreases. In Fig. 13, the influence of inside to outside pressure on the dimensionless response system tois presented. By increasing inside to outside pressure, the dimensionless response system toof microbeam increases.Figure 14 depicts the effect of temperature change on dimensionless response system to, could be seen with increasing temperature change of system the excitation frequency of microbeam decreases, so that one of the approach for control of system is changing temperature change. Figure 15 shows that with increasing of angular velocity, the stiffness and excitation frequency of microbeam decreases so that the maximum amplitude of system decreases.

Fig. 6. Effect of material length scale parameter on the dimensionless natural frequency (Vcnt = 0.12, R/h = 50, T = 300 K, Hx = 0, m = 1).

Fig. 7. Effect of volume fraction of CNT on the dimensionless response system (L/R = 80, R/h = 50, Hx = 0, T0 = 300 K, = 0, = 600 rad/s, Pi1/Po1 = 2, Pi2 /Po2 = 4, l/h = 10, n = 10).

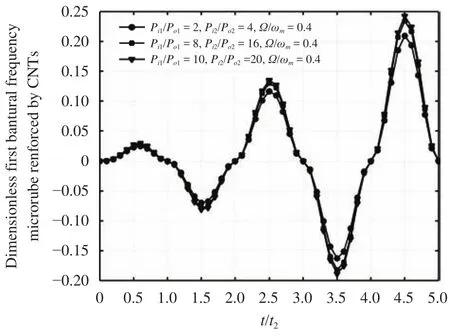
Fig. 8. Effect of inside to outside pressure on the dimensionless response system (L/R = 80, R/h = 50, Vcnt = 0.12, Hx = 0, T0 = 300 K,= 0, = 600 rad/s, l/h = 10, n = 10).

Fig. 9. Effect of inside to outside temperature on the dimensionless response system (L/R = 80, R/h = 50, Vcnt = 0.12, Hx = 0, = 0, =600 rad/s, Pi1/Po1 = 2, Pi2/Po2 = 4, l/h = 10, n = 10).

Fig. 10. Effect of angular velocity on the dimensionless response system (L/R = 80, R/h = 50, Vcnt = 0.12, Hx = 0, T0 = 300 K, = 0,Pi1/Po1 = 2, Pi2/Po2 = 4, l/h = 10, n = 10).

Fig. 11. Effect of magnetic field on the dimensionless response system for (L/R = 80, R/h = 50, Vcnt = 0.12, T0 = 300 K, = 0, =600 rad/s, Pi1/Po1 = 2, Pi2/Po2 = 4, l/h = 10).

Fig. 12. Effect of volume fraction of CNT on the dimensionless response system for (L/R = 80, R/h = 50, Hx = 0, = 600 rad/s, T0= 300 K, = 0, Pi1/Po1 = 2, Pi2/Po2 = 4, l/h = 10).

Fig. 13. Effect of inside to outside pressure on the dimensionless response system to (L/R = 80, R/h = 50, Vcnt = 0.12, Hx = 0.5 MA/m, T0 = 300 K, = 0, = 600 rad/s, l/h = 10).

Fig. 14. Effect of inside to outside temperature on the dimensionless response system for (L/R = 80, R/h = 50, Vcnt = 0.12, Hx =0.5 MA/m, = 0, = 600 rad/s, Pi1/Po1 = 2, Pi2 /Po2 = 4, l/h = 10).

5 Conclusions

A theoretical analysis on free and forced vibration characteristic of nano-composite microbeam is carried out in the present work. The Hamilton principle and Euler–Bernoulli beam theory are considered to derive the equations of motion. Navier’s type solution is employed to obtain the natural frequency of nanocomposite microbeam. The effects of various parameters such as: magnetic field, volume fraction of CNT, temperature, material length scale parameter on the natural frequency and response system of nano-composite microbeam are investigated. Also, the effects shock of change, the external force in different period of time on response system for nano-composite microbeam based on modified couple stress theory is novelty of the present paper.Manufacturing sensors, displacement fluid, and drug delivery is the practical aspect of this research. The results of this research are listed as follows.

Fig. 15. Effect of angular velocity on the dimensionless response system for (L/R = 80, R/h = 50, Vcnt = 0.12, Hx = 0.5 MA/m, T0 =300 K, = 0, Pi1/Po1 = 2, Pi2 /Po2 = 4, l/h = 10).

(1) For nano-composite microbeam, natural frequency increases with increasing volume fraction of CNT and material length scale parameter because the stiffness of nano-composite microbeam enhances.

(2) By increasing magnetic field, the stiffness of system decreases so that the natural frequency decreases. Also, one of the best methods to control of the micro beam system and increasing the stability of this system is applied the magnetic field.

(3) With increasing of temperature change, the stiffness of system decreases so that the natural frequency decreases. Also,the elasticity module of resin and matrix and molecular force between resin and matrix decreases by increasing the temperature change so that the dimensionless natural frequency decreases.

(4) By increasing the volume fraction of CNTs, the system becomes stiffer, so that the amplitude of response of system will not significant change.

(5) By increasing the deference pressure between inside and outside can be caused the increasing of external force. So that with passing of time the amplitude of microbeams increases.

(6) With increasing of volume fraction of CNT and magnetic field, maximum amplitude system reduces.

(7) With increasing of angular velocity, the stiffness and excitation frequency of microbeam decreases so that the maximum amplitude of system decreases.

(8) With increasing inside to outside pressure and material length scale parameter, maximum amplitude of system increases.

(9) Also, to control the vibration amplitude of smart materials, the researchers need the sensor and actuator to decrease the vibration amplitude, thus employing the electro-dynamic Maxwell's equations in the nano-composite microbeam can be helped us to reach this goal. It is noted that the authors follow this goal in future works.

Acknowledgments

The authors are thankful to the Iranian Nanotechnology Development Committee for their financial support and the University of Kashan (463855/7).

References

[1]S. Ijjima, Helical microtubules of graphitic carbon, Nature 354(1991) 56–58.

[2]C.W. Lim, C. Li, J.L. Yu, Dynamic behaviour of axially moving nanobeams based on nonlocal elasticity approach, Acta Mech.Sin. 26 (2010) 755–765.

[3]L. Wang, Size-dependent vibration characteristics of fluid-conveying microtubes, J. Fluid. Strcut. 26 (2010) 675–684.

[4]M. Ghannad, M. Zamani Nejad, G.H. Rahimi, Elastic solution of axisymmetric thick truncated conical shells based on first-order shear deformation theory, Mechanika. 79 (2009) 13–20.

[5]C.X. Xue, E. Pan, Q.K. Han, et al., Non-linear principal resonance of an orthotropic and magnetoelastic rectangular plate,Int. J. Nonlinear. Mech. 46 (2011) 703–710.

[6]Y. Bayat, M. Ghannad, H. Torabi, Analytical and numerical analysis for the FGM thick sphere under combined pressureand temperature loading, Arch. Appl. Mech. 82 (2012) 229–242.

[7]A. Ghorbanpour Arani, M.R. Mobarakeh, Sh. Shams, et al., The effect of CNT volume fraction on the magneto-thermo-electromechanical behavior of smart nanocomposite cylinder, J.Mech. Sci. Tech. 26 (2012) 2565–2572.

[8]M. Ghannad, H. Gharooni, Displacements and stresses in pressurized thick FGM cylinders with varying properties of power function based on HSDT, J. Solid Mech. 4 (2012) 237–251.

[9]J. Kim, J.N. Reddy, Analytical solutions for bending, vibration,and buckling of FGM plates using a couple stress-based thirdorder theory, Compos. Struct. 86 (2013) 86-98

[10]A.V. Lopatin, E.V. Morozov, Buckling of the composite orthotropic clamped-clamped cylindrical shell loaded by transverse inertia force, Compos. Struct. 95 (2013) 471–478.

[11]H. Shen, Y. Xiang, Post buckling of nanotube-reinforced composite cylindrical shells under combined axial and radial mechanical loads in thermal environment, Compos. Part B-Eng. 52(2013) 311–322.

[12]M. Ghannad, H. Gharooni, Displacements and Stresses in rotating FGM pressurized thick hollow cylinder with exponentially varying properties based on FSDT, Tech. J. Eng. Appl. Sci. 3(2013) 1790–1799.

[13]L. Zhang, X. Li, Buckling and vibration analysis of functionally graded magneto-electro-thermo-elastic circular cylindrical shells, Appl. Math. Model. 37 (2013) 2279–2292.

[14]M. Mohammadimehr, A.H. Rahmati, Small scale effect on electro-thermo-mechanical vibration analysis of single-walled born nitride nanorods under electric excitation, Turk. J. Eng. Env.Sci. 37 (2013) 1–15.

[15]A.E. Alshorbagy, Temperature effects on the vibration characteristics of a functionally graded thick beam, ASEJ. 4 (2013)455–464.

[16]Y.S. Li, Z.Y. Cai, S.Y. Shi, Buckling and free vibration of magneto electro elastic nanoplate based on nonlocal theory, Compos. Struct. 111 (2014) 522–529.

[17]O. Rahmani, O. Pedram, Analysis and modeling the size effect on vibration of functionally graded nanobeams based on nonlocal Timoshenko beam theory, International Journal of Engineering Science 77 (2014) 55–70.

[18]L.W. Zhang, Z.X. Lei, K.M. Liew, Free vibration analysis of functionally graded carbon nanotube-reinforced composite triangular plates using the FSDT and element-free IMLS-Ritz method, Compos. Struct. 120 (2015) 189–199.

[19]A.H. Rahmati, M. Mohammadimehr, Vibration analysis of nonuniform and non-homogeneous boron nitride nanorods embedded in an elastic medium under combined loadings using DQM, Physica. B. 440 (2014) 88–98.

[20]A.H. Sofiyev, N. Kuruoglu, Buckling and vibration of shear deformable functionally graded orthotropic cylindrical shells under external pressures, Thin Walled Struct. 78 (2014) 121–130.

[21]H. Shen, Y. Xiang, Nonlinear vibration of nanotube-reinforced composite cylindrical panels resting on elastic foundations in thermal environments, Compos. Struct. 111 (2014) 291–300.

[22]M.R. Nami, M. Janghorban, M. Damadam, Thermal buckling analysis of functionally graded rectangular nanoplates based on nonlocal third order shear deformation theory, Aero. Sci.Technol. 41 (2015) 7–15.

[23]R. Ansari, R. Gholami, M.F. Shojaei, et al., Bending, buckling and free vibration analysis of size-dependent functionally graded circular/annular microplates based on the modified strain gradient elasticity theory, Eur. J. Mech. A-Solid 49 (2015)251–267.

[24]M. Mohammadimehr, M. Mohandes, M. Moradi, Size dependent effect on the buckling and vibration analysis of double-bonded nanocomposite piezoelectric plate reinforced by boron nitride nanotube based on modified couple stress theory, J. Vib.Control. 22 (2016) 1790–1807.

[25]C. Du, Y. Li, X. Jin, Nonlinear forced vibration of functionally graded cylindrical thin shells, Thin Walled Struct. 78 (2014)26–36.

[26]X. Ma, G. Jin, Y. Xiong, et al., Free and forced vibration analysis of coupled conical-cylindrical shells with arbitrary boundary conditions, Int. J. Mech. 88 (2014) 122–134.

[27]A. Ghorbanpour Arani, S. Amir, P. Dashti, et al., Flow-induced vibration of double bonded visco-CNTs under magneticfields considering surface effect, Comp. Mater. Sci. 86 (2014) 144–154.

[28]L. Ke, S. Wang, Free vibration of size-dependent magnetoelectro-elastic nanobeams based on the nonlocaltheory, Pyhsica. E.63 (2014) 52–65.

[29]Y.T. Beni, F. Mehralian, H. Razavi, Free vibration analysis of size-dependent shear deformable functionally graded cylindrical shell on the basis of modified couple stress theory,Compos. Struct. 120 (2015) 65–68.

[30]R. Ansari, E. Hasrati, M.F. Shojaei, et al., Forced vibration analysis of functionally graded carbon nanotube-reinforced composite plates using a numerical strategy, Pyhsica. E. 69 (2015)294–306.

[31]M.Z. Nejad, M. Jabbari, M. Ghannad, Elastic analysis of axially functionally graded rotating thick cylinder with variable thickness under non-uniform arbitrarily pressure loading, Int. J. Eng.Sci. 89 (2015) 86–99.

[32]L. Lü, Y. Hu, X. Wang, Forced vibration of two coupled carbon nanotubes conveying lagged movingnano-particles, Eur. J.Mech. A-Solid 68 (2015) 72–80.

[33]H. Salehipour, H. Nahvi, A.R. Shahidi, Exact closed-form free vibration analysis for functionally graded micro/nano plates based on modified couple stress and three-dimensional elasticity theories, Compos. Struct. 124 (2015) 283–291.

[34]S. Ziaee, Small scale effect on linear vibration of buckled sizedependent FG nanobeams, Ain Shams Eng. J. 6 (2015) 587–598.

[35]A. Ghorbanpour Arani, M.S. Zarei, Nonlocal vibration of Y-haped CNT conveying nano-magnetic viscous fluid under mag-netic field, Ain Shams Eng. J. 6 (2015) 565–575.

[36]A. Ghorbanpour Arani, Z.K. Maraghi, A feedback control system for vibration of magnetostrictive plate subjected to follower force using sinusoidal shear deformation theory, Ain Shams Eng. J. 7 (2016) 361–369.

[37]H. Zeighampour, Y.T. Beni, Cylindrical thin-shell model based on modifiedstrain gradient theory, Int. J. Eng. Sci. 78 (2014)27–47.