一种新的空间分离矢量天线阵列和叉积测向算法

李 阳

(中国西南电子技术研究所，四川 成都 610036)

电磁矢量天线具有能够完整地感知入射电磁信号的极化信息，提高波达角DOA参数估计精度，和接收宽带信号等优点[1].在信号检测和侦收等场景下，没有必要使用测量所有电磁分量的矢量天线[2].传统电磁矢量天线共点的天线单元之间，互耦效应无法忽略时，采用空间分离的极化敏感阵列是一个更好的选择[3].虽然有许多互耦参数估计算法，但是最简单有效的方法还是简化天线结构，增加阵元之间的间距，从而减小互耦效应带来的影响.空间分离的偶极子天线和/或环形天线构成的极化敏感阵列，具有结构简单和隔离度高的特点，此外还增大了天线的孔径，提高了入射信号参数估计的精度.文献[4]提出了一种直线型的空间分离矢量天线阵列(Spatially Spread Electro-Magnetic Vector Sensor, SSEMVS)，并给出了利用矢量叉积估计信号DOA参数的确定性算法.但是直线性的空间分离矢量天线阵列的几何构型为直线，不能有效地利用空间，对DOA参数的估计可能存在模糊，同时确定性DOA参数估计算法的精度可以进一步提高.文献[5]研究了一般的SSEMVS，分析了基于矢量叉积的测向算法及其唯一可辨识性.文献[6]将空间分离的偶极子天线引入极化多输入多输出(MIMO)雷达系统中，降低互耦并利用极化信息.文献[7]结合叉积算法和相位干涉法获取两维波达角估计.

传统的叉积算法，将电场分量和磁场分量的共轭进行矢量叉积运算，归一化后得到入射电磁信号的单位方向矢量，和一个单位复数矢量对应元素相乘的哈达玛乘积.根据乘积的解析结构，设计了高效和高精度的参数估计算法，即枚举非线性规划算法.文献[4]推导了已知信号波形时DOA和极化参数估计的克拉美劳界(Cramér-Rao Bound, CRB)，而枚举非线性规划算法可以有效地逼近CRB.

本文对叉积算法进行分析，考察电场分量和磁场分量的多种叉积运算组合，发现其它叉积组合的结果，同样具有入射电磁信号单位矢量和一个单位复数矢量的哈达玛乘积结构.这些叉积组合结果和传统坡印廷矢量表达式不同，且是测量噪声统计独立的新叉积结构，据此提出一种新的SSEMVS和叉积测向算法.分析表明，一般的SSEMVS的辨识性分析结果和DOA估计算法经过修改，同样适用新的矢量天线阵列结构，实现入射信号的波达方向DOA估计.

1 数据模型

在忽略本征阻抗和射频通道之间的一致性之后，电磁矢量天线的输出阵列流形矢量为aEMVS=[eThT]T，与入射信号的波达角和极化参数之间的关系为[1]：

(1)

其中θ∈[0,π],φ∈[0,2π) 分别为俯仰角和方位角，γ∈[0,π/2],η∈(-π,π] 分别为极化辅助角和极化差异角，ex,ey,ez表示偶极子天线单元测得的电场分量，hx,hy,hz表示环形天线单元测得的磁场分量.

一般的SSEMVS，通过将电磁矢量天线的6个天线单元在三维空间中平移分开布置构成，如图1所示.在这样的布置结构中，每个偶极子天线(环形天线)的取向分别平行于(垂直于)x，y和z坐标轴.平移分开的天线单元，在接收入射信号时，在各个天线单元上产生与相对位置有关的相位差.在天线坐标系中，当各环形天线的位置矢量用pHx,pHy,pHz，偶极子天线的位置矢量用pEx,pEy,pEz表示时，由天线单元位置差异引起的相位矢量为：

(2)

其中ps为入射电磁信号的坡印廷矢量.

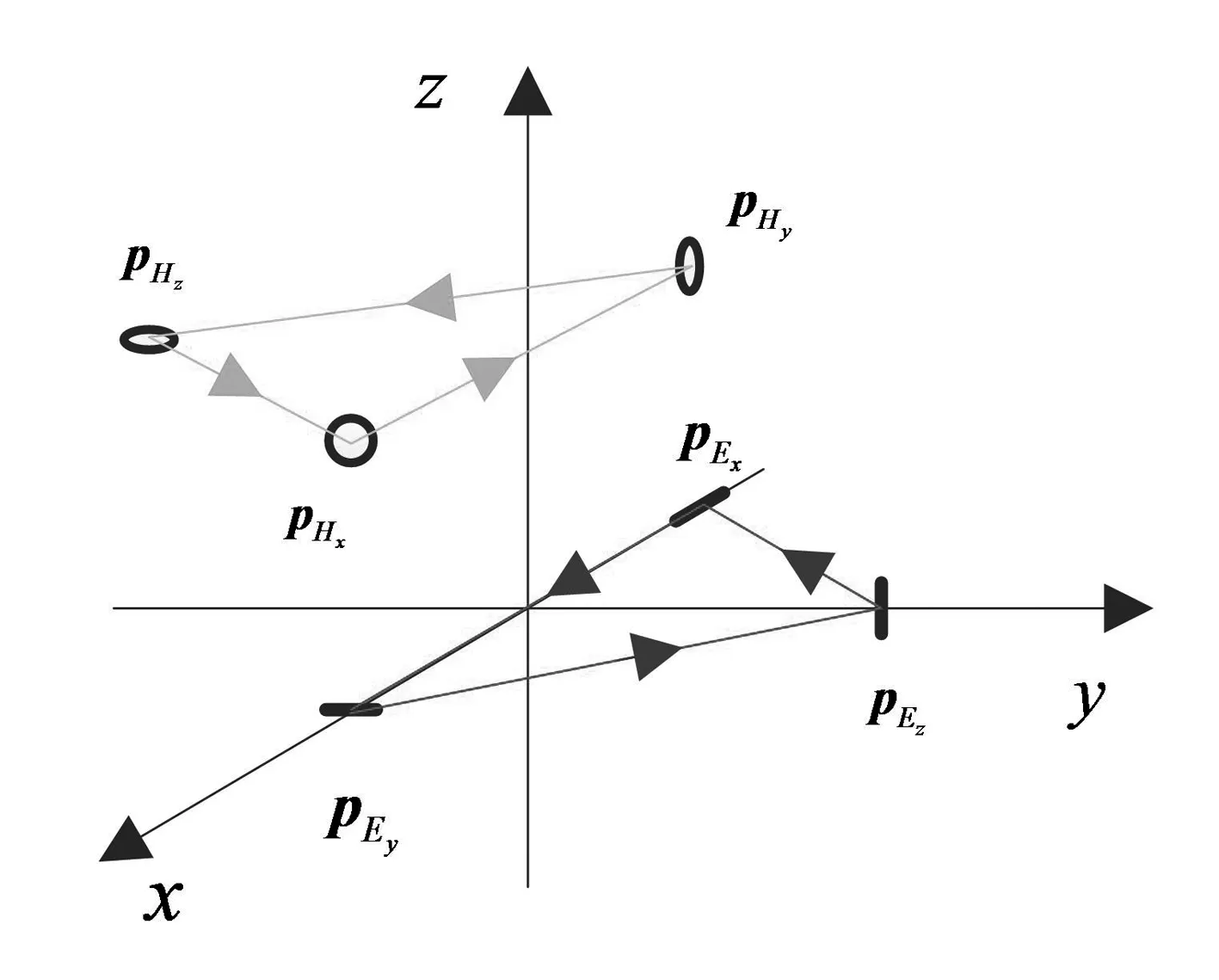
图1 一般的空间分离矢量天线

结合式(1)和式(2)可以得到，一般SSEMVS的阵列流形矢量：

a(θ,φ,γ,η)=aEMVS(θ,φ,γ,η)·d(θ,φ),

(3)

其中·为对应元素相乘的哈达玛乘积.在加性高斯噪声假设下，当多个信号入射时，可以得到SSEMVS阵列的接收数据模型：

(4)

其中Y为接收数据矩阵，ak,k=1,…,K为第k个信号入射方向的阵列流形矢量，sk,k=1,…,K为第k个信号的时域波形采样快拍，N为测量噪声.

2 新的叉积算法和新的SSEMVS

2.1 不同组合的叉积运算

电磁矢量天线的输出阵列流形矢量式(1)可以重新表示为：

(5)

其中h,v为定义信号坐标系水平和垂直方向的单位实矢量，Eh,Ev为入射信号在水平和垂直方向分量的复解析表示：

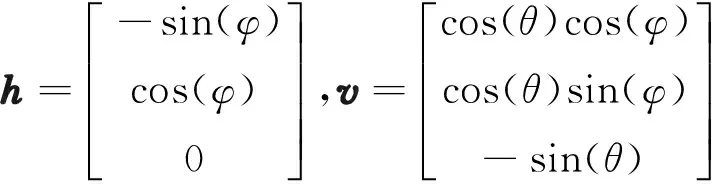
(6)

Eh=cos(γ),Ev=sin(γ)ejη.

信号坡印廷矢量ps是与波矢k同向的单位实矢量.h，v和ps构成右手坐标系，根据矢量叉积的性质有：

(7)

根据式(5)和式(7)可以推导传统计算坡印廷矢量的叉积算法：

(8)

类似地，通过电场和磁场复解析表示的实部和虚部分别进行叉积运算，发现同样可得到信号的坡印廷矢量信息，即如下四种组合：

(9)

其中Re(·)和Im(·)分别表示取实部和取虚部运算.在实际中，圆复高斯噪声假设下，实部和虚部测量噪声独立，阵列流形矢量估计受到不同噪声影响，式(9)中的估计相互独立，那么通过将它们进行融合可得到统计更优的估计，如文献[8]中e1和e2的融合方法.值得注意的是，通过对e1和e2的归一化可以得到ps的准确估计，而e3和e4归一化后则可能得到方向相反的-ps.在复数框架下的叉积估计式以及H不取共轭的叉积估计都是ei,i=1,2,3,4的某种确定性组合，可以验证：

E×H*=e1+e2,

(10)

E×H=e1-e2+(e3+e4)j.

(11)

2.2 新的空间分离矢量天线阵列

新的叉积结构式(11)，具有入射信号坡印廷矢量和未知复数矢量哈达玛积时，可以应用文献[5]中的DOA估计算法.本文称这种阵列为新的SSEMVS阵列.为了推导与新的叉积结构相适应的SSEMVS阵列，首先给出引理1.

引理1 当向量a,b,c,d∈3×1，满足b和d的叉积为零时，即：

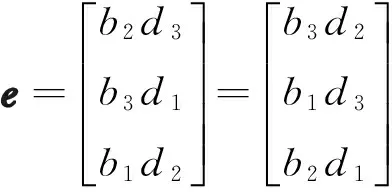
(12)

则如下等式成立：

a·b×c·d=e·a×c.□

(13)

证明：根据哈达玛乘积和矢量叉积的定义将式(13)的左边展开可得：

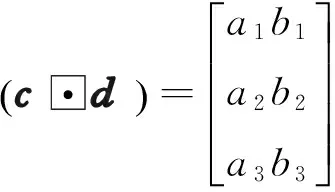
(14)

将式(12)代入式(14)，并根据矢量叉积的定义可得：

e·a×c,

(15)

同时有：

b×d=e-e=0.□

(16)

根据上述新的叉积定义，得到如下新的SSEMVS阵列结构.

定理1 (新的SSEMVS)当三个与坐标轴x,y,z平行的偶极子天线的位置矢量pEx,pEy,pEz，以及三个取向与坐标轴x,y,z平行的环形天线的位置矢量pHx,pHy,pHz满足如下反对称关系时：

(17)

阵列流形的矢量叉积式(11)，可以表示为信号坡印廷矢量与一个单位复数矢量的哈达玛乘积再乘上一个复系数：

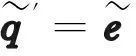
(18)

其中：

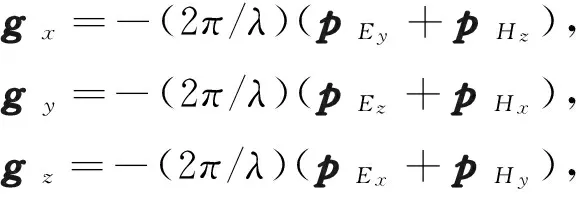
(19)

ps是入射信号坡印廷矢量，λ为阵列信号的工作频率对应的波长.gx,gy,gz称为新的SSEMVS阵列的g参数.□

(20)

利用引理1可知在de平行于dh时，记为de‖dh时有：

(21)

而de‖dh等价为：

de×dh=0,

(22)

即：

(23)

若对任意方向入射ps均成立，那么有：

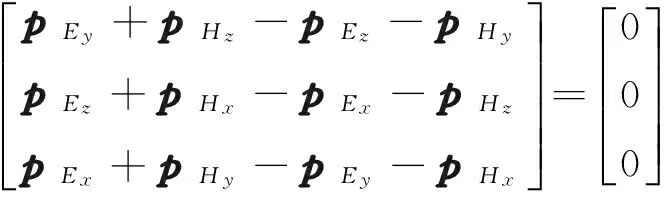
(24)

即等价于式(17).□

基于g参数的模糊性分析和枚举非线性规划算法估计信号的波达角参数[5]同样适用于该新的SSEMVS阵列.

3 仿真结果

(25)

(26)

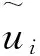
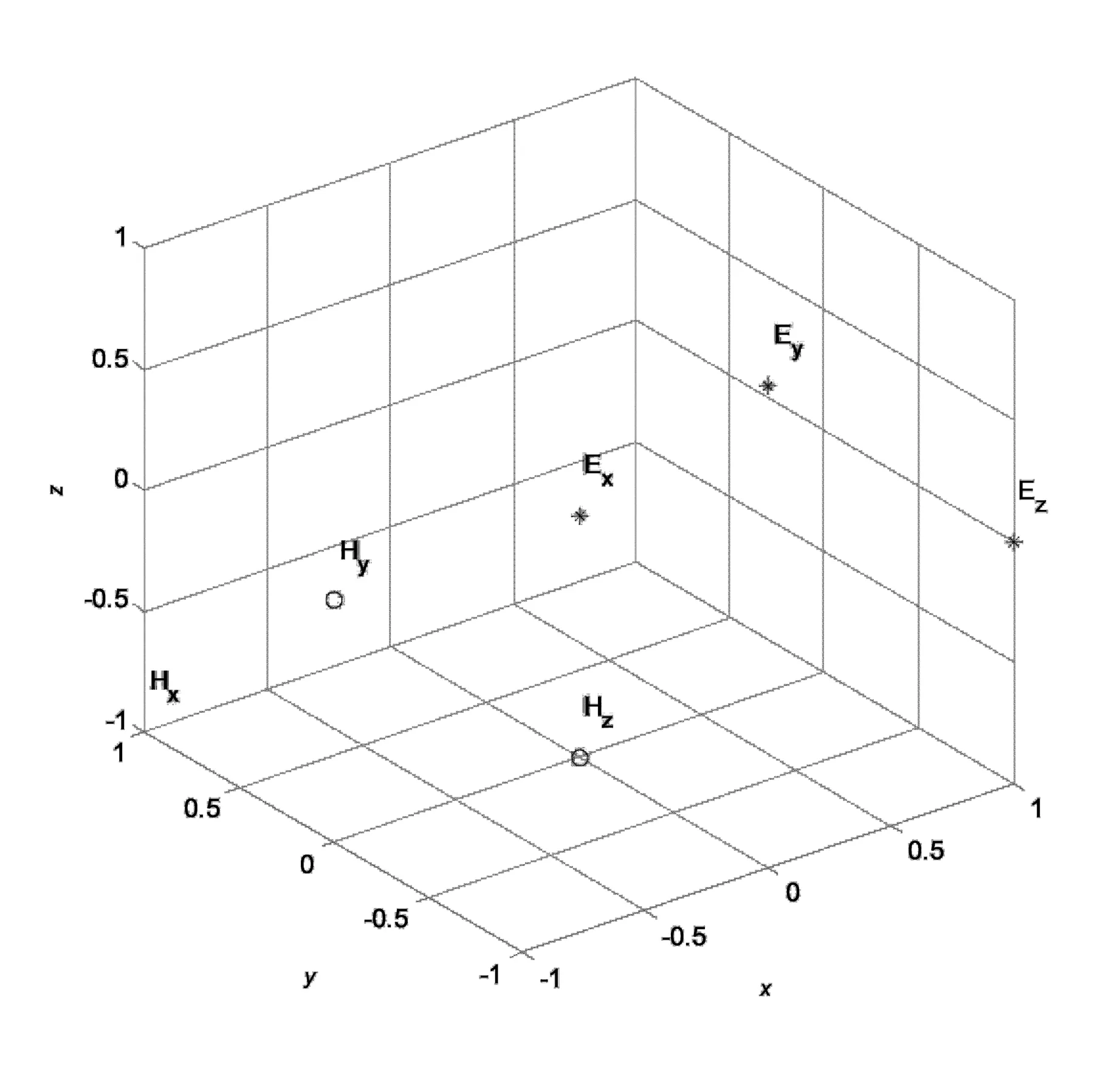
图2 阵列的阵元位置分布，星号表示偶极子天线，圆圈表示环形天线

A. 实验1：两个信号入射波达角CRB的比较

这个实验考察新SSEMVS天线单元之间的距离对DOA估计算法性能的影响.考虑两个入射信号，DOA和极化参数(θ,φ,γ,η)分别为(35°,42°,45°,10°)和(43°,35°,45°,170°)，基带频率分别为f1=0.1，f2=0.1265.信噪比为30dB.实验结果如图3所示.从图中可以看出，与前面的SSEMVS阵列类似，两个信号源参数估计的CRB均随天线单元之间的间距的增大而减小.

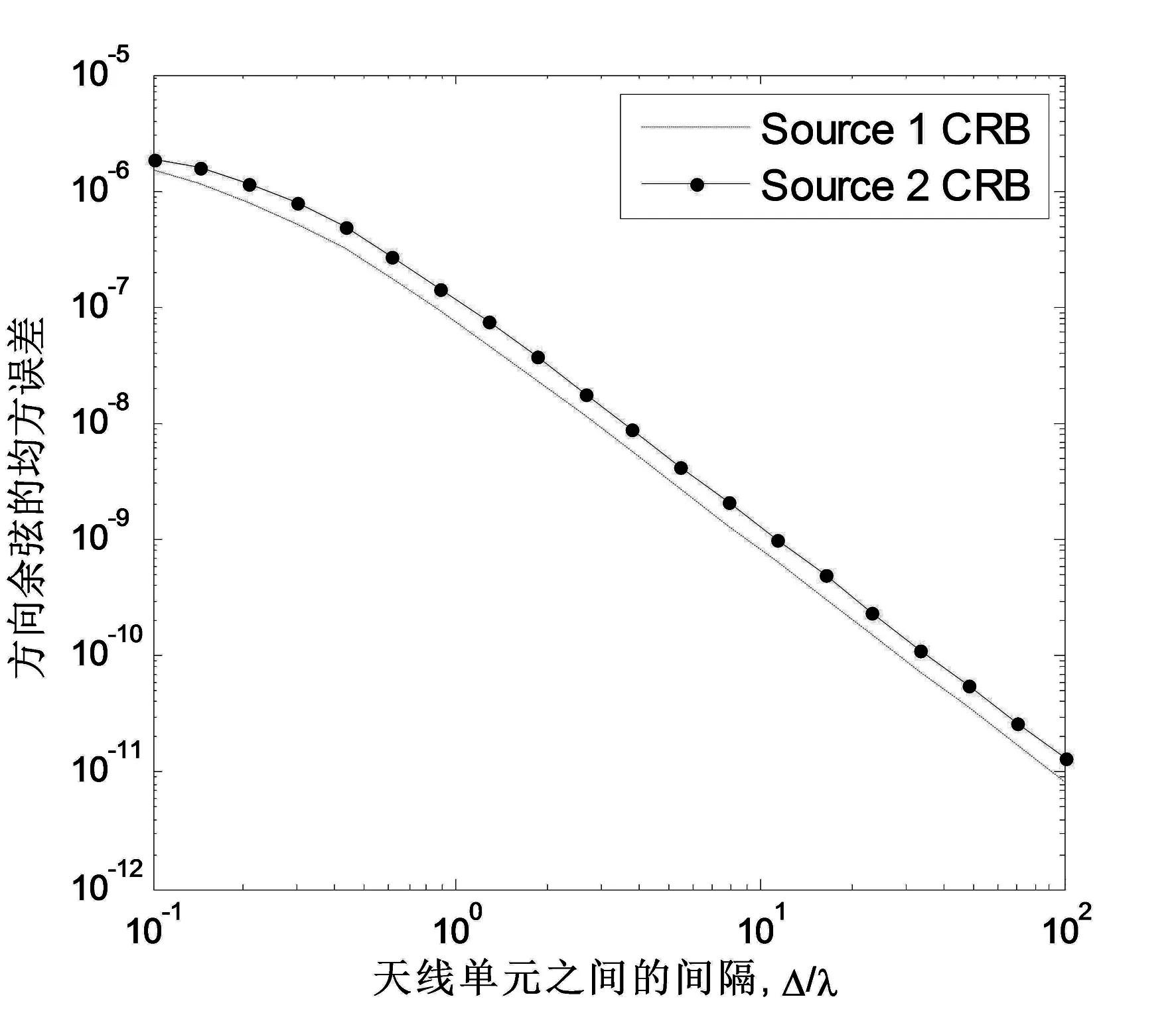
图3 新SSEMVS阵列中坡印廷矢量估计的CRB随天线单元之间距离的变化

B.实验2：两个信号入射波达角MSE的比较

这个实验考察在新SSEMVS天线单元之间的距离对DOA估计性能的影响.两个入射信号配置与实验1相同.实验结果如图4所示.从图中可以看出，与前面的SSEMVS阵列类似，在天线单元之间间距在十个波长以内时枚举非线性规划算法均能正确地估计信号波达角，且有效的达到CRB；不过，随着天线单元间距继续增大，在决定信号坡印廷矢量的符号时出现错误，导致均方差急剧增大.

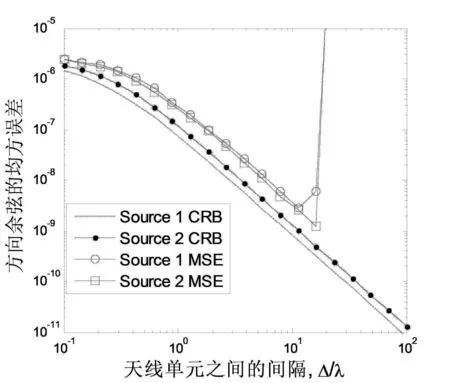
图4 新SSEMVS阵列中信号坡印廷矢量估计的均方误差随天线单元之间距离的变化

C. 实验3：不同间距叉积向量拟合误差曲面

更了进一步验证图4中“拐点”出现的原因，这里给出叉积向量拟合误差随信号到达角θ和φ的变化，结果如图5和图6所示，其中z轴对应拟合误差的负对数，值越大对应误差越小.实验配置与实验2相同.从图中可以看出当天线单元之间间距较小时，拟合误差“谱”的峰值相对较少，但也不止一个，这意味着初值选择不当时，优化很容易收敛到错误的局部极值，不过根据幅度信息来确定初值，仍然能够有效的求解得到正确的估计；当天线单元之间间距增大时，拟合误差“谱”的峰值急剧增多，使得优化陷入错误的局部最优的可能也随之增大，当幅度信息提供的初值精度不够时，则出现了图4中的“拐点”.

图5 第一个信号叉积向量拟合误差曲面

图6 第二个信号叉积向量拟合误差曲面

4 结论

本文分析了电场分量和磁场分量实部和虚部不同组合下的叉积结构，分析表明传统的叉积运算只是这些叉积结果的一种组合.在此基础上，给出了电场分量和不取共轭的磁场分量之间的叉积所定义的叉积测向，给出了适合枚举非线性规划算法的新空间分离矢量天线阵列结构.与传统SSEMVS相比，完善了叉积估计算法的理论架构，提供了更加灵活的阵列布局.仿真验证了新的SSEMVS和新的叉积测向算法的正确性和有效性.

参考文献：

[1]徐友根,刘志文,龚晓峰.极化敏感阵列信号处理[M].北京:北京理工大学出版社,2013.

[2]Tabrikian J, Shavit R, Rahamim D. An efficient vector sensor configuration for source localization [J]. IEEE Signal Processing Letters, 2004,(8): 690-693.

[3]See C M S, Nehorai A. Source localization with distributed electromagnetic component sensor array processing [A]. Proceedings of International Symposium on Signal Processing and Its Applications[C]. New York:IEEE,2003: 177-180.

[4]Wong K T, Yuan X. “Vector cross-product direction-finding” with an electromagnetic vector-sensor of six orthogonally oriented but spatially noncollocating dipoles/loops [J]. IEEE Transactions on Signal Processing, 2011, (1): 160-171.

[5]Li Y, Zhang J Q. An enumerative nonLinear programming approach to direction finding with a general spatially spread electromagnetic vector sensor array [J]. Signal Process, 2013,(4): 856-865.

[6]Zheng G M, Zhang D. BOMP-based angle estimation with polarimetric MIMO radar with spatially spread crossed-dipole [J]. IET Signal Process, 2018, (1): 113-118.

[7]郑桂妹, 陈伯孝, 杨明磊. 新型拉伸电磁矢量传感器的两维高精度波达方向估计[J]. 系统工程与电子技术, 2014, (7):1282-1290.

[8]Jiang J F, Zhang J Q. A weighted inner product estimator in the geometric algebra of euclidean 3-space for source localization using an EM vector-sensor [J]. Chinese Journal of Aeronautics, 2012, (1): 83-93.