盲生数学缺失补偿教学之探索

● 孟宪军

由于盲生视觉感官缺陷，其生活和学习也呈现许多缺失的现象。一是生活常识缺失；二是准确感知缺失；三是基础知识缺失；四是学习自信缺失。依据《盲校义务教育数学课程标准》中提出的“如何进一步发挥学生多重感官的功能，开发优势潜能，培养学生的素养”这一核心问题，在实际教学中，笔者围绕盲生数学缺失补偿进行了一些探索。

一、对缺失补偿实践之探索

（一）从“局部感知补偿”到注重“整体感知补偿”

在进行盲生局部感知补偿时，常常会出现“盲人摸象”的现象。根据《盲校义务教育数学课程标准》中潜能开发与缺陷补偿原则，我们要充分调动学生多重感官参与学习，最大限度地调动学生的潜能。

如在进行“鸡兔同笼”问题教学时，为了铺垫及了解盲生生活常识储备情况，笔者请一位全盲学生回答：一只鸡有几条腿？该盲生迟疑一会儿后回答道：可能有3条腿吧。再问他为什么，他说：不知道，是猜的。这正是盲生因视觉的缺失，导致生活常识的缺失。为了能让该生感知鸡的腿数，老师在课堂上扮演“鸡”，让他去摸，然后再问他：鸡有几条腿？他答道：3条。为了解学生的感知与思维过程，教师继续问：为什么？该生回答道：我摸的有 1、2、3，3条腿。事实上，出现这种“盲人摸象”现象，只因局部感知补偿不足所致。为此，教师依据注重感知的原则，对没有形成有效补偿的，采取新的策略，重新进行补偿。为此，教师让该生扮演“鸡”，让他摸数自己扮演的“鸡”的腿。这样盲生就利用自身肢体感知弥补了局部感知补偿不足的问题。

实践经验：利用自己的身体进行整体感知，能够弥补盲生感官缺失的缺陷，比局部感知的补偿效果好。

（二）从“演绎推算”到注重“归纳补偿”

引导盲生化演绎推算为归纳补偿，增强解题的直观性。虽然这种逆向的解题方式不如演绎推算规范，但有利于盲生探究出问题的结果，切合《盲校义务教育数学课程标准》中多渠道辅助教学的原则：充分考虑实物、模型、触摸图对学习内容和方式的影响，把直观教学手段作为学生学习的有力工具，有效改进教与学的方式。

如：一根比地球最大横切面周长还长6.28米的铁丝与地球最大横切面围成同心圆，铁丝与地球之间的缝隙能穿过一只小老鼠吗？

对此问题，教师本想通过引导学生通过演绎推算的方式，逐步转化解决。可引导盲生探究时，却启而不发，这是教师备课时没能注意到的问题。推算演绎法行不通，该如何进行缺失补偿？根据盲生直观感知能力强的生理特点及注重感知的原则，我们不妨尝试一下实验归纳法。为此，教师找来两根长长的绳子，使两绳相差6.28米。然后，组织盲生将两绳围成两个同心圆，围成后请全体盲生走进缝隙。全盲学生通过触摸感知，弱视学生近距离观察与测量，他们惊奇地叫道：“缝隙怎么这么大？”经过反复实践观察、触摸感受，他们推断铁丝与地球之间的缝隙能够穿过一只小老鼠。这种“化演绎为归纳”的方法，通过盲生的感知，强化了缺失补偿，从而落实了由浅入深的教学策略。

实践经验：化演绎推算为归纳补偿的方法，让盲生推测出问题的结果，正契合了伽利略所说的：一切推理都必须从观察与实验得来。对盲生而言，这也是一种有效的解题途径与活动经验，对增强他们的学习自信心同样具有重要价值。

（三）从“抽象概括”到注重“具象补偿”

盲生因视觉缺陷，抽象概括能力欠缺。课题组成员围绕缺失补偿，引领盲生从具象补偿中感悟知识的生成。如教学“角的初步认识”，虽然角在生活中随处可见，但在视障儿童的头脑中，却是一个模糊的概念，他们分不清生活中的角（脚、角）和数学意义上的角。为了避免盲生产生混淆，教学一开始，教师就通过实际操作，让盲生直观感知，帮助他们在初步认识长方形、正方形、三角形的基础上，体会角的基本图形。

实践经验：以身体之，以心悟之，以盲生敏感的触觉来补偿视觉缺失是非常有效的学习方法。

二、对缺失补偿策略之探索

盲生以听觉、嗅觉、味觉和皮肤感觉等补偿视觉缺失。在实践活动中，笔者提炼了相关缺失补偿的学习策略。

（一）肢体感知的补偿策略

在教学中，我们针对盲生认知的不完整性，利用盲生自身肢体强化整体感知的补偿。如在“线段垂直平分线”课堂教学中，笔者引导盲生利用“站位”探究线段两端距离相等点的位置。开始探究时，学生都集中“挤”到线段的中点。在直观感知中，部分学生提出质疑，并逐步分散，站成了一条线，进而探究出到线段两端距离相等的点的分布特征：这些点构成这条线段的垂直平分线。学生利用站位，形成对视觉缺失的补偿。这种将画图探究改为站位探究的做法，有效利用盲生肢体感知的直观性与整体性，对盲生形成了有效补偿，提高了教学的有效性。

（二）由浅入深的补偿策略

从中学生的心理特点来看，整个中学阶段，学生的思维能力处于快速发展时期：七年级学生的思维以形象为主，九年级学生的思维倾向于经验性和逻辑性。对于盲生来讲，在初中阶段仍然是以形象思维为主，小学阶段的盲生更是如此。所以，教学活动中要达成由浅入深的策略，我们首先坚持引导的直观性，其次坚持引导的本质性。

如盲生问：如何将23.26°化为度分秒？思考：学生为什么感到困难？如何由浅入深地引导探究？引导探究：请问23.2元能化为几元几角？请问23.26元能化为几元几角几分？（引导探究算法）请问元角分是多少进位制？度分秒是多少进位制？（引导探究算理）能否类比元角分问题的转化将23.26°化为度分秒？教师引导学生类比关于元角分转化的问题，探究算法和算理，进而探究关于度分秒问题的解题方法。

（三）学以致用的补偿策略

教师应引导学生多思考、多交流，以用促学，发掘学生实践中的特色做法与智慧，逐步形成学以致用的补偿策略。如盲生数学活动：探究到不在一条直线上的三点A、B、C距离相等的点O的位置。教师采取合作拉绳实验的方法代替文本画图探究。此实验对弱视学生注重了感知，形成了补偿；对全盲学生，虽然实验中也注重让他们触摸感受，但由于绳子较长，再加上全盲学生的方向感不强，他们没有整体感知，当然也没能形成更好的补偿。正当教师在苦苦思索补偿对策时，发现低视力学生甲与全盲学生乙，一人用两个手指代替不在一条直线上的两根绳子，另一人也用两根手指分别表示这两根线段的垂直平分线，这两根垂直平分线的交点正是所求的点。这样全盲学生乙就有了整体感知，问题迎刃而解。此法在全班交流，对全体同学的启发效果非常明显。

盲生个体差异大，教师应将低视力学生与全盲学生合理分组，让优秀学生在学以致用中展示与交流，实现了个体化教学补偿，并逐步提炼学以致用的补偿策略。

三、对缺失补偿范式之探索

（一）对缺失补偿教学范式的界定

笔者尝试将“缺失补偿教学范式”这一概念界定为：对盲生因视觉感官缺陷造成的缺失，进行补偿与潜能开发，并逐步构建有利于盲生进步或发展的教学“典范”或“模式”。其缺失补偿教学主题提炼为：“注重感知、形成补偿、由浅入深、学以致用。”

（二）对缺失补偿教学模型的构建

笔者根据缺失补偿教学主题，初步构建“缺失补偿”理念下的教学模型：

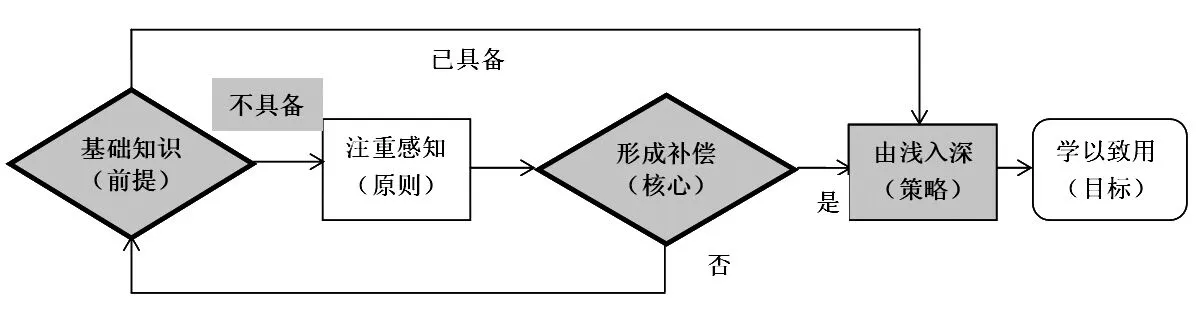
整个过程以盲生基础知识为补偿的前提，以注重感知为补偿的原则，以由浅入深为补偿的策略，以学以致用为补偿的目标，以“形成补偿”为核心。

（三）对缺失补偿教学模型的优化

前期构建的初步模型，有两个方面的判断：一是判断盲生生活常识或基础知识是否需要补偿；二是判断基础知识是否形成补偿。从实践探索中，笔者认识到还需对“由浅入深（策略）”补偿方法的有效性进行判断。为此，在深度构建中，将“由浅入深（策略）”改进为“菱形判断框”。这样缺失补偿形成了三个层面：一是注重感知形成基础补偿；二是由浅入深形成策略补偿；三是学以致用形成应用补偿。

（四）缺失补偿教学模型的衍生

该模型是原模型的操作衍生图，分别由学生、教师操作流程构成。学生“自判缺失、感知探究、学以致用”体现了学生学习的主体性；教师“评判缺失、引导探究、由浅入深”体现了教师的主导性。衍生操作模型的构建，明确了学生、教师各自独立且又互通的操作模式。整个过程中的每一个环节均以“形成补偿”为核心，从而进一步深化和完善了缺失补偿的教学范式。

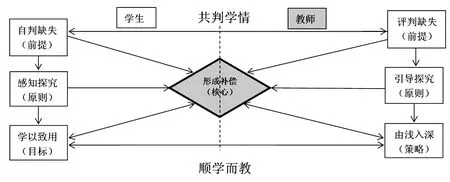
综上所述，所谓“缺失补偿教学范式”也可概括为：根据盲生缺失情况，以补偿方式、补偿策略、补偿活动等作为缺失补偿教学的自变量，以形成补偿促进盲生有效学习作为缺失补偿教学的因变量的教学模式或典范。

参考文献：

［1］任涛.盲校义务教育数学课程标准解读［J］.现代特殊教育，2017（2）.

［2］金美月.义务教育数学课程标准（2011年版）案例式解读［J］.辽宁教育，2012（13）.

［3］王洪伟.课堂实现有效教学若干因素的研究［J］.基础教育，2006（12）.

［4］周小山.当代教学范式研究［J］.陕西师范大学学报（哲学社会科学版），2004（5）.