古汉语使动双宾语语句的逻辑语义分析

(四川师范大学 逻辑与信息研究所，成都 610066)

古汉语中双宾语出现的频率很高，因此，对古汉语进行研究必须对双宾语加以关注。双宾语语句可表示为S. V←Om←Op，其中，Om是移动性宾语(即直接宾语)，Op是表象性宾语(即间接宾语)[1]100。例如，在《前汉书》卷三十五中有一句“太后赐张卿千金”，此处“张卿”就是表象性宾语Om，“千金”是移动性宾语Op。一般说来，古汉语中的双宾语句具有三个语法特征：(1)Op与Om之间没有任何结构上的关系；(2)Op与Om可分别和介词搭配构成介宾短语且充当原述宾短语的修饰或补充成分；(3)双宾句的深层结构为NPSV NPPNPm[1]100。

在古汉语中，使动双宾语语句是双宾语语句中一个特殊的门类，该句式的主语和表象性宾语Op都指人物，一般表示Op在主语的作用下接受Om所指的结果。这类双宾语的语序是固定的，Op靠近动词，处于近宾位，Om处于远宾位[1]101。例如，在《左传·僖公二十七年》中有：“国老皆贺子文，子文饮之酒。”“饮之酒”中的“之”，指代国老，为Op成分，而“酒”则为Om，其大意即“子文使国老饮酒”。

一般而言，自然语言(古汉语也不例外)都具有组合性。换句话说，复合语言表达式的意义是由其直接成分的意义同有关句法结构运算的意义组合而成[2]8，因此，在对自然语言进行信息处理时，组合性原则是考虑问题的出发点[3]83。本文主要目的就是研究如何组合性地分析古汉语使动双宾语语句的逻辑语义，即如何逐次递增地处理和翻译随之而来的每一个基本单位。为了能够组合性地对双宾语语句的语义进行精准的形式化处理，就需要制定一些句法和语义规则，并需要对将要用到的范畴逻辑[4]和类型λ-演算[5]328-334(不妨统称为范畴类型逻辑)知识进行必要的分析。

一

范畴类型逻辑是一种使用运算和推演的手段，描述自然语言的形式化工具。其基本思想是：语言认知就是数学计算，语法分析就是逻辑推演，即：“认知=计算；语法=逻辑；分析=推演”[4]1。范畴类型逻辑遵循句法与语义的对应原则：句法结构每运算一次，与之相应的语义就组合一次。

在范畴逻辑中，np表示名词短语的范畴，s表示语句的范畴，nps表示不及物动词的范畴，(nps)/np表示及物动词的范畴。不及物动词nps需要向左毗连一个名词np，才能够组合成一个语句s，因此在nps中的“”不妨叫作向左毗连算子。及物动词(nps)/np首先需要向右毗连一个名词短语np，组合成一个不及物动词短语nps，然后再向左毗连一个名词短语np，才能够组合成一个语句s，因此(nps)/np中的“/”不妨叫作向右毗连算子。

本文将用到的句法语义并行运算规则有：

规则1：毗连算子的消除规则

规则2：毗连算子的引入规则

规则3：竖线算子的引入规则与消除规则

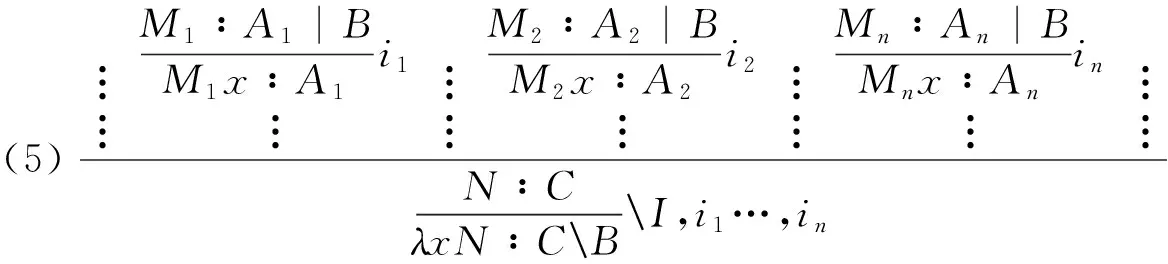
为了能够对代词进行指代消解，本文还需要引入指代算子“|”。之所以引入该算子，是因为单独为代词指派句法范畴的时候，代词可以被视为缺乏先行词的专名或普通名词。若直接指派范畴np，则无法表达代词与其对先行词之间的指代照应关系；而引入指代算子“|”，便可较好的解决这一问题。我们为代词指派的范畴是np|np，其意思是，如果在范畴为np|np的代词左边，有一个范畴为np的先行词，那么此时代词的作用与范畴为np的先行词的作用是一样。当为代词指派范畴后，便可通过假设或加标运算消去指代算子。

在本文中，用“赵盾′”表示词条“赵盾”的语义词项，其他类似。

利用范畴逻辑中的范畴运算，可以实现词条句法方面的组合，但要实现词条语义方面的组合翻译，则需要类型λ-演算。这是因为λ-算子可以为自然语言中的各种表达式提供形式上的翻译[6]112。具体地说，λ-算子能够使我们通过对变元的抽象，由一个表达式得到另一个新的表达式[6]104。例如，如果α是类型论语言L中类型为a的表达式，v是类型为b的变元，那么λvα就是类型为〈b,a〉的表达式。

二

下面我们利用以上讨论的范畴逻辑和类型λ-演算，同时从句法和语义两个方面组合性地对古汉语使动双宾语语句的逻辑语义进行分析。

1.“晋侯饮赵盾酒”的逻辑语义分析

这个例子在大多数古汉语的论文文献中被提及，并且引起过争议。因为若不联系上下文，单独看这个句子，它是有歧义的。第一种语义解读是：晋侯饮赵盾的酒，晋侯是“饮”这个动作的施行者，赵盾是“酒”的限定词，整个句子是一个普通的主谓句。第二种语义解读是：晋侯使赵盾饮酒，“饮”这个动词的施动者为赵盾，整个句子就变成了使动双宾语。从《左传·宣公二年》整篇的内容来看，当取第二种解读。

现在，我们就“晋侯饮赵盾酒”第二种语义解读“晋侯使赵盾饮酒”中的及物动词“饮”的语义进行翻译。由于及物动词“饮”既要与位于其右边的范畴为np的直接宾语“赵盾”(其范畴为np)进行毗连，又要与位于其右边的范畴为np的间接宾语“酒”进行毗连，形成范畴为nps的不及物动词短语，这一不及物动词短语再与范畴为np的“晋侯”进行毗连，最后组合成范畴为s的语句，因此带有双宾语的及物动词“饮”的句法范畴应该是[(nps)/np]/np。

对于“饮”的语义分析则比较复杂，本文参照Dowty系统中make(使)的语义翻译，将“使”翻译为λXλPλxP(λy(∃Q(Q(x)CAUSEX(y))))[7]109。由于“饮”在古汉语中有“使……饮”之意，但“饮”本身是一个及物动词，因此笔者对这一翻译稍作改动，即：“饮”翻译为λx(λyz(∃Q(Q(x)CAUSE饮′(y，z))))。仔细对比这两个翻译,就可以发现，笔者是将Dowty系统中算子CAUSE后的一元谓词表达式X(y)|，转换成了二元关系谓词表达式“饮′(y,z)”。

利用句法语义运算规则以及使动词“饮”的语义翻译，就可以通过树形图的方法，形式化表示出“晋侯饮赵盾酒”句法运算和语义组合过程，即把自然语言语句翻译成相应的逻辑表达式，其中词条之间的范畴运算表示的是句法运算过程，而对于它的λ-演算则表示的是语义组合翻译过程。“晋侯饮赵盾酒”第二种解读的句法运算和语义组合翻译过程如图1所示。

图1 “晋侯饮赵盾酒”语义推导

2.“殴民而归之农”的逻辑语义分析

此句出自贾谊的《论积贮疏》，其中，“归”作为使动词，在此处译为“使……归”，“之”和“农”分别作为间接宾语和直接宾语。笔者之所以选取该句作为第二个例句，是由于这是一个包含有更多处理技巧的复杂句式。首先，该句子从成分上来看主语缺失，所以只能处理成一个谓语动作句，在处理过程中需要假设一个主语，并且最后要消除假设；其次，这里的联结词“而”，起到了并列动作的作用，即“殴民”与“归之农”两个动作是由同一个主语做出的，所以这个“而”字要处理成合取的语义表达式；第三点，则是该句出现了代词“之”，所以需要对其指代项进行指代消解处理。

我们利用第二部分给出的相关规则就可以形式化地表示“殴民而归之农”的句法运算和语义组合了，其具体过程请见图2。

nps

图2 “殴民而归之农”的语义推导

从图2可看出，“殴民而归之农”被指派的句法范畴是nps，这与不及物动词短语的范畴是一样的，这是因为该语句本身缺少主语，其结构自然就相当于不及物动词短语。但是，为了对这一语句进行处理，假设了一个范畴为np的主语语迹j；为了对范畴为np|np的代词“之”进行消解，把其范畴假定为np，我们最后得到的“殴民而归之农”语义表达式为λx.(殴′(x,民′)∧∃Q(Q(x)CAUSE归′(民′，农′)，其意思是：某x，x殴民，并且x的某个行为Q导致民归农。

三

从本文的两个实例可以得出如下结论。(1)由于使动双宾语句的结构是固定的，因此，本文的研究方法具有普适性。具体地说，本文对古双宾语语句的句法运算和语义的组合翻译的处理方式，可以推广到对同类型的双宾语语句的处理。(2)利用范畴类型逻辑对古汉语使动双宾语语句进行逻辑分析时，句法和语义的组合可以同时在树结构中展示出来，句法组合伴随了语义方面的函数应用。(3)利用范畴逻辑可以从句法方面组合性地分析古汉语中使动双宾语语句。之所以能够做到这一点，是因为范畴语法中的范畴表示了一个词条符号如何与另一个词条符号进行组合[8]4。(4)与英语一样，古汉语中词条符号的语义部分可以通过类型λ-演算来表示，这是因为λ-算子具有能够使我们通过对变元的抽象，由一个表达式得到另一个新的表达式的能力[6]102。

事实上，λ-算子是标注函数符号的算子，是形式语言中常用的算子，能够为诸多计算提供统一的处理。而且λ-算子使得我们能够在形式语言中创造新的复合函数符号，能够形式化地准确表示新的复合函数的性质[9]203。那么，我们如何挖掘类型λ-演算和范畴语法的潜力，组合性的翻译和处理古汉语其他类型的语句(比如兼语句、连动句等)，从而为中文信息处理作出应有的贡献？这有待我们做进一步的深入研究。

参考文献:

[1]时兵.古汉语双宾句再认识[J].安徽大学学报(哲学社会科学版)，1999，(6):100-106.

[2]邹崇理.逻辑、语言和蒙太格语法[M].北京:社会科学文献出版社,1995.

[3]张晓君，郝一江.动态谓词逻辑的动态机制[J].哲学动态，2010，(9):83-89.

[4]邹崇理.范畴类型逻辑:从语言到逻辑[M].北京:中国社会科学出版社，2008.

[5]蔡曙山,邹崇理.自然语言形式理论研究[M].北京:人民出版社,2010.

[6]GAMUT L T F.Logic,Language,andMeaning,VolumeII：IntensionalLogicandLogicalGrammar[M]. Chicago: The University of Chicago Press, 1991.

[7]DOWTY D R.WordMeaningandMontagueGrammar[M]. Dordrecht: D. Reidel Publishing Company, 1979.

[8]JÅGER G.AnaphoraandTypeLogicalGrammar[M]. Berlin：Springer, 2005.

[9]维·马奇舍夫斯基.现代逻辑词典[K].张兆梅,等译.北京:中国人民大学出版社,1992.