基于参考信号的广义特征值分解盲源分离算法及其在北斗多路径效应削弱中的应用

陈 健，岳东杰，刘志强，朱少林，陈 浩

（河海大学 地球科学与工程学院，南京 211100）

全球导航卫星系统（Global Navigation Satellite System, GNSS）动态测量误差主要包括星历误差、卫星及接收机钟差、电离层及对流层延迟误差、多路径误差和仪器测量噪声等。在短基线定位解算中，通过差分法和误差改正模型等方法能基本消除绝大部分的测量误差，然而由于多路径误差、随机噪声的站间相关性很小，无法用上述方法消除[1-2]。GPS多路径效应特性与削弱方法得到国内外许多专家学者的深入研究，其中主要包括多路径重复性改正模型和频域滤波两类方法[3]。多路径重复性改正是GNSS天线的位置及其周围环境基本不变或变化很小时，多路径效应误差具有较强的周日重复性的特点，在监测点不动时进行静态观测提取多路径模型。Mosavi M R等[4]根据多路径误差按恒星日周期变化的特点，用小波变换（Wavelet Transform, WT）方法分离出GNSS信号中的多路径误差；Zhong[5]利用恒星日滤波和交叉证认的小波滤波进行多路径误差削弱；Azarbad M R[6]利用Wavelet对多路径误差进行建模并有效地削弱了多路径误差。频域滤波法是根据多路径误差主要部分表现为低频，而振动位移信号相对为高频，通过小波滤波方法直接提取振动位移信号。崔冰波[7]提出利用经验模式分解（Empirical Mode Decomposition, EMD）方法对多路径误差进行建模和削弱；卢辰龙、陈德忠[8-9]分别提出奇异谱滤波（Finite Impulse Response, FIR）以及观测值域双差残差恒星日滤波方法进行多路径误差削弱；罗飞雪[3]等提出利用参考经验模式分解-独立分量分析（Independent Component Analysis, ICA）方法进行多路径建模和削弱。

北斗导航定位系统（Beidou Navigation Satellite System, BDS）是我国正在实施的自主发展、独立运行的全球卫星导航系统。与美国的 GPS、俄罗斯的GLONASS使用MEO星座不同，BDS系统包含三种星座类型，即GEO、IGSO、及MEO卫星。近年来，BDS观测值质量分析以及多路径效应削弱方法一直是国内外学者们研究的热点。Montenbruck等[10]利用北斗三频观测数据分析了北斗信号和观测值质量，得出严重的多路径效应会影响精密单点定位的收敛速度和可靠性的结果；唐卫明等[11]通过削弱多路径效应，有效提高了模糊度的固定效率；王广兴等[12]研究表明BDS多路径效应有明显的日周期特性，并提出了削弱多路径误差的相关方法；Dong D等[13]提出了多路径半天球图（Multipath Hemispherical Map, MHM），实现了多路径效应的实时在线解算和改正；Dai W等[14]对MHM 算法和恒星日滤波算法进行了对比分析，并提出了多路径误差参数化改进模型。尽管多路径效应具有日周期性，但随着时间的推移，由于卫星轨道微小变化等原因，多路径效应的相关性会逐渐降低；鉴于此，本文针对BDS动态监测中多路径效应误差日周期性的特性，对广义特征值分解（Generalized Eigen-value Decomposition, GED）盲源分离算法进行了扩展，提出了基于参考信号的 GED盲源分离方法来削弱多路径误差的影响，并通过仿真数据以及实验观测数据对该方法进行了验证。

1 一种基于参考信号的广义特征值盲源分离算法

1.1 广义特征值分解盲源分离算法

一般的线性混叠形式，其数学模型可表示为：

构造如下的广义特征值问题：

将式(1)代入式(4)化简得到：

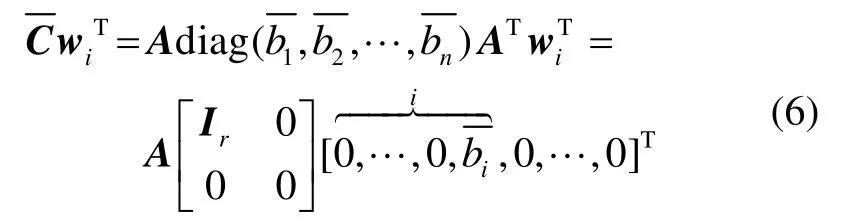
类似于上面的运算有：

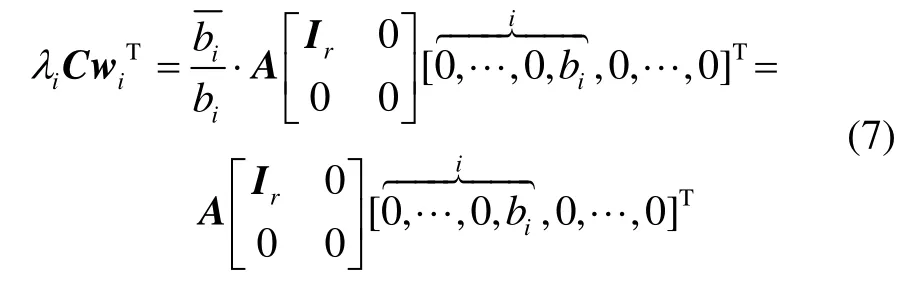
由式(6)(7)知：

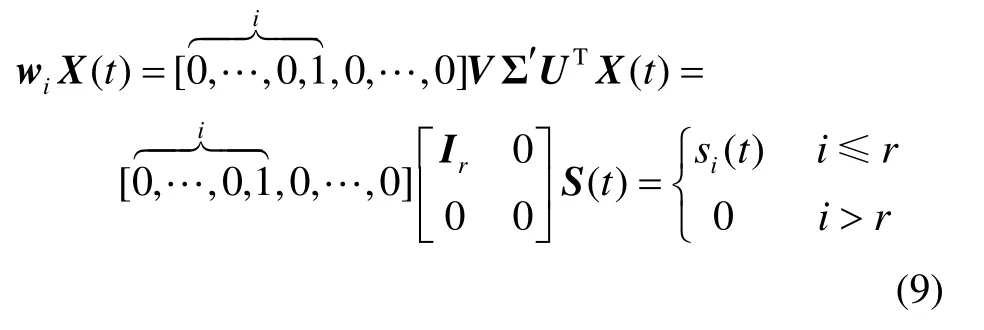
由于广义特征值问题(3)最多有n个不同的特征值，其对应的特征矢量相互正交，且由式(9)知是恢复信号。由此可知，只要求出广义特征值问题(3)的r个相互正交的特征矢量即可分离出r个源信号。

由广义特征值盲源分离的原理可以看出：广义特征值盲源分离需要处理的输入信号必须是多个，且分解出来的独立分量具有幅值不确定性[15]。BDS动态监测应用中只有一个坐标残差序列为输入信号，因此本文通过EMD方法将单信号分解成多信号，将复杂的信号分解成高频到低频排序的模态函数（Intrinsic Mode Function, IMF）分量，并提取复杂信号的趋势项。将 EMD和广义特征值盲源分离结合起来可较好地解决单通道信号分离问题。

1.2 基于参考信号的GED盲源分离算法对BDS多路径效应削弱

基于GED盲源分离算法可知，其存在不确定性：分离信号排序不确定性、相位不确定性、幅值不确定性。目前通过相关性以及频谱相似测度来消除不确定性。文献[16]不仅有效消除了盲源分离估计的幅值与相位不确定性，而且较准确地实现了混合矩阵的参数辨识，但排序的不确定依然存在。文献[17]基于相关系数法消除了盲源分离信号的排序和相位的不确定性。本文在文献[17]的基础上提出了基于参考信号的广义特征值盲源分离算法。其算法步骤如下：

1）将第1天静态观测数据的原始坐标残差序列通过奇异谱分析（Singular Spectrum Analysis, SSA）去噪，其结果作为多路径误差模型的初始参考信号ir；

2）对后面一天的原始坐标序列进行EMD分解，得到R个IMF分量；

3）将步骤2）中EMD分解后得到的IMF分量作为虚拟观测数据利用广义特征值盲源分离的方法获取当天多路径误差信号yi；

4）求振幅恢复比例系数a，其中，n为历元数。

2 仿真实验分析

为了解本文算法在信号中分离的效果，假设模拟信号由4个独立信号组成，分别为：

4）随机信号：

其中：N为数据容量，取N=1000，v=[0：N-1]。得到原始数据的波形图如图 1(a)所示，然后将原始数据用一个4×4的随机构成的混合阵混合，得到如图1(b)所示混合后的信号，利用本文算法对混合后的信号进行分离，如图1(c)所示。

对比图 1(a)和 1(c)可知，通过广义特征值盲源分离后，信号的波形得到很好的恢复，分离信号与对应的源信号相关系数均接近 1，表明利用本文算法能有效地进行分离。

图1 模拟信号Fig.1 Analog signal

3 数据试验与结果分析

数据采集地点设在河海大学某楼顶，周围有产生多路径效应的强反射面。基线长度约为4 m，采集时间自2016年01月31日至2016年2月9日（共10天），采样间隔为30 s，卫星高度角为10°。通过单历元解算得到移动站北(N)、东(E)、天(U)方向坐标残差序列。为了更清晰地观察坐标序列的趋势以及对比分析，将各天的观测数据绘于同一图中，如图2所示（限于篇幅，本文以 E方向为例，各天的坐标残差序列依次增加常数20 mm）。

由于基线长度较短，载波差分技术基本上可以消除卫星与接收机钟差、对流层与电离层误差以及卫星轨道误差等，然而多路径误差与仪器噪声的站间相关性很小，无法得到消除，此时可以认为坐标残差序列主要包含随机噪声和多路径误差。相邻两天以及第1天与后面各天 3个方向上的坐标残差序列相关系数如图3所示。

从图2可以得到：连续10天的坐标残差序列具有很强的重复性（第1天中第三小时左右受到突变型误差影响），不仅含有高频的随机噪声，而且含有低频的多路径效应误差。从图 3（上）可以得到：随着时间的增加，后面各天 N、E、U方向坐标残差序列与第一天的坐标残差序列相关系数呈明显下降趋势，最小值达到0.5；从图3（下）可以得到：相邻两天的N、E、U方向坐标残差序列具有很强的相关特性，相关系数都在0.7以上，最大值达到0.95。由此可以看出，低频部分的多路径效应存在重复性特性，证明了利用此特性削弱多路径误差的可行性。因此，本文使用奇异谱分析方法进行消噪处理，可以得到第1天残差序列中精确的多路径误差模型，用于后面各天的多路径误差改正。图4为第1天E方向坐标残差序列以及多路径误差改正模型。

图2 E方向的原始坐标序列Fig.2 Raw coordinates of E direction

图3 各天坐标残差序列相关系数（上：第1天与后面各天相关系数；下：相邻两天相关系数）Fig.3 Correlation coefficients (up: the first multipath series and the others; down: two days consecutive multipath series)

为了对比分析本文所提出的基于参考信号的GED盲源分离算法与重复性建模方法削弱多路径误差的效果，现采用两种方案分别对后面9天的坐标残差进行处理。

方案1：采用后面9天E方向坐标残差序列减去第一天的多路径误差改正模型，图5所示为E方向处理之后的残差序列图；

方案 2：采用本文提出的基于参考信号的 GED盲源分离算法进行多路径误差改正，同时更新多路径误差改正模型。图6所示为E方向处理之后的残差序列图，图7所示为E方向多路径误差模型；

为了定量分析两种方案的定位精度，分别计算出均方根误差，见表3（Bef为N、E、U方向处理之前的RMS统计结果，P1为方案1处理之后的RMS统计结果，P2为方案2处理之后的RMS统计结果）。

1）从表3可知：对比N、E、U方向RMS统计结果，其中U方向坐标残差序列的RMS值最大，约为N方向的3倍、E方向的15倍，即高程方向受随机噪声和多路径效应影响最大。N方向坐标序列的RMS值大于E方向，主要原因是BDS星座以GEO和IGSO卫星为主。

图4 第1天E方向残差序列和多路径误差改正模型图Fig.4 Coordinate series of residual and multipath error correction mode in E direction of the first day

图5 方案1处理之后的E向残差序列图Fig.5 Coordinate series of residuals in E-direction after processing by scheme 1

图6 方案2处理之后的E向残差序列图Fig.6 Coordinate series of residuals in E-direction after processing by scheme 2

2）从图5和表3中P1列可知：当误差改正模型时间间隔较短时，方案1中重复性建模方法能够比较有效地削弱多路径效应影响，但随着时间间隔的增加（本算例约为6天），均方根误差值突然增加，多路径误差改正模型已经不能有效地削弱多路径误差影响。

3）从图6～7可以得到：10天的多路径效应具有较强的重复性；将图5与图6，表3中P2列与P1进行对比分析：方案2中各天的均方值呈现平稳趋势且定位精度要优于方案1，表明方案2中基于参考信号的 GED盲源分离算法不仅能有效地削弱多路径效应的影响，而且能够较好地更新多路径误差模型，减缓随着时间间隔增加多路径误差模型改正效果快速降低的过程。

图7 方案2 处理之后的E向多路径误差序列图Fig.7 Multipath error series in E-direction after processing by scheme 2

表3 改正前、后坐标序列的RMS值Tab.3 RMS of coordinate series before and after multipath correction mm

4 结 语

本文充分利用广义特征值盲源分离方法的优点，提出一种基于参考信号的 GED盲源分离算法，用于多路径效应的建模和削弱。通过实验表明：该算法能够提取更为精确的多路径模型，在一定程度上解决了固定多路径模型随着时间推移重复性减少且有效性降低的问题，其多路径改正效果要优于重复性建模的改正效果。从本文的研究可以看出，广义特征值的盲源分离算法在测量数据处理中有着广阔的应用前景，但实际应用效果还需验证，其理论与算法还有待于进一步完善。

参考文献（References）：

[1]李豹, 许江宁, 曹可劲, 等. 北斗二代导航信号抗多径性能分析与仿真[J]. 中国惯性技术学报, 2012, 20(3):339-342.Li B, Xu J N, Cao K J, et al. Analysis and simulation on anti-multipath performance of Beidou2 navigation[J].Journal of Chinese Inertial Technology, 2014, 22(3):339-342.

[2]于帅. GNSS变形序列多尺度分析与建模方法研究[D].安徽: 安徽理工大学, 2016.Yu S. Research on multiscale analysing and modelling of GNSS deformation series[D]. Anhui: AnHui University of Science and Technology, 2016.

[3]罗飞雪, 戴吾蛟, 唐成盼, 等. 参考经验模态分解独立分量分析及其在GPS多路径误差处理中的应用[J]. 测绘学报, 2012, 41(3): 366-371.Luo F X, Dai W J, Tang C P, et al. EMD-ICA with reference signal method and its application in GPS multipath[J]. Acta Geodaetica et Cartographica Sinica,2012, 41(3): 366-371.

[4]Mosavi M R, Azarbad M R. Multipath error mitigation based on wavelet transform in L1 GPS receivers for kinematic applications[J]. Aeu-international Journal of Electronics and Communications, 2013, 67(10): 875-884.

[5]Zhong P, Ding X L, Yuan L G, et al. Sidereal filtering based on single differences for mitigating GPS multipath effects on short baselines[J]. Journal of Geodesy, 2010,84(2): 145-158.

[6]Azarbad M R, Mosavi M R. A new method to mitigate multipath error in single-frequency GPS receiver with wavelet transform[J]. GPS Solutions, 2014, 18(2): 189-198.

[7]崔冰波, 陈熙源. 基于一种改进EMD算法的GPS多路径效应抑制方法[J]. 中国惯性技术学报, 2014, 22(3):346-351.Cui B B, Chen X Y. Multipath mitigation of GPS signal based on improved EMD algorithm[J]. Journal of Chinese Inertial Technology, 2014, 22(3): 346-351.

[8]卢辰龙, 匡翠林, 易重海, 等. 奇异谱分析滤波法在消除 GPS多路径中的应用[J]. 武汉大学学报(信息科学版), 2015, 40(7): 924-931.Lu C L, Kuang C L, Yi Z H, et al. Singular spectrum analysis filter method for mitigation of GPS multipath error[J]. Geomatics and Information Science of Wuhan University, 2015, 40(7): 924-931.

[9] 陈德忠, 叶世榕, 刘炎炎, 等. 基于观测值域的GPS多路径误差应用分析[J]. 武汉大学学报(信息科学版),2014, 39(2): 147-151.Chen D Z, Ye S R, Liu Y Y, et al. Applied analysis of GPS multipath errors based on observation domain[J].Geomatics and Information Science of Wuhan University,2014, 39(2): 147-151.

[10]Oliver M, Andre H, Peter S, et al. Initial assessment of the compass/BeiDou-2 regional navigation satellite system[J]. GPS Solutions, 2013, 17(2): 211-222.

[11]Tang W M, Deng C L, Shi C, et al. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J].GPS Solutions, 2013, 18(3): 335-344.

[12]Wang G X, Kees de Jong, Zhao Q L, et al. Multipath analysis of code measurements for BeiDou geostationary satellite[J]. GPS Solution, 2015, 19(1): 129-139.

[13]Dong D, Wang M, Chen W, et al. Mitigation of multipath effect in GNSS short baseline positioning by the multipath hemispherical map[J]. Journal of Geodesy, 2016,90(3): 255-262.

[14]Dai W, Shi Q, Cai C. Characteristics of the BDS Carrier phase multipath and its mitigation methods in relative positioning[J]. Sensors, 2017, 17(4): 796.

[15]赵燕, 缪善林. 基于广义特征值分解的盲源分离的盲信号分离算法[J].中国电子科学研究院学报, 2012, 7(2):208-211.Zhao Y, Miao S L. Blind signal separation algorithm based on generalized eigen-decomposition[J]. Journal of CAEIT, 2012, 7(2): 208-211.

[16]焦卫东, 杨世锡, 钱苏翔, 等. 基于 FFT-MCC 分析的ICA(BSS)盲源不确定性消除[J]. 中国机械工程, 2006,17(7): 673-676.Jiao W D, Yang S X, Qian S X, et al. A new method for recognition of independent noise sources of complex system under strong noisy environment[J]. China Mechanical Engineering, 2006, 17(7): 673-676.

[17]金桂梅, 李永冰, 张丽. 基于相关系数的盲源分离排序和相位调整法[J]. 通信与信息技术, 2010(3): 55-58.Jin G M, Li Y B, Zhang L. Phase adjustment and sequence of blind source separation based on correlation[J]. Communication & Information Technology, 2010(3):55-57.