卫星观测信号盲源分离算法

2022-05-11刘国光

测绘技术装备 2022年1期

刘国光

(广州南方测绘科技股份有限公司，广东广州 510665)

1 引言

多频混合信号的处理方法研究一直是信号处理的重点。一些常规的信号处理方法，如奇异值分析、主成分分析等，对混叠信号处理后的输出结果都是相互之间信号，不能够保证输出的所有结果信号实现对源信号的最佳表现。随着信号处理技术的发展，衍生出如经验模式分解、小波分析与傅里叶变换等现代信号处理方法。但是这些方法对于多信号混叠的处理效果均不好，不能有效地分离出混叠信号。随着信息学科、神经网络学科、统计学科等学科的发展，也涌现出一些信号混叠盲源分离算法。

盲源信号分离算法是通过获取的观测信号特性对信号进行处理的方法，并且此观测信号的混叠方式是未知的。“盲源”主要是指对源信号几乎没有先验知识的条件下，通过推导获取混合参数，从而实现信号的盲源分离。经过专家学者的多年研究，已经提出大量的盲源分离算法，比如基于最大信噪比算法、独立分量分析算法等。目前盲源分离算法已经应用于图像处理、雷达、语音等多个领域，成为当前的研究热点。然而，常规的盲源分离算法忽略了源信号可以被多次拷贝输出的问题，认为所有的源信号只要被重构一次就可以实现源信号的有效分离。因此，如果真正需要实现源信号的有效分离，还要了解其他相关信号处理技术等。针对常规盲源分离算法的缺点，本文提出一种新的盲源分离方法。该方法针对观测信号的多路径误差特征，并且利用盲源分离算法在处理多源信号中的优势，研究从全球导航卫星系统(Global Navigation Satellite System，GNSS)观测信号中分离出的多路径误差。本文从信号处理的角度出发，为盲源分离在GNSS观测数据处理中的应用进行了有益的探索。

2 盲源分离经典算法

经过多年研究，盲源分离的理论与实践体系已经相对完善，盲源分离方法可根据不同的分类标准分为多种类型：一是按照时间延迟将盲源分离分为瞬时混合模型与卷积混合模型，二是按照映射关系将盲源分离分为非线性和线性盲源分离，三是按照观测通道数量将盲源分离分为欠定盲源分离、等定盲源分离和超定盲源分离[1]。

2.1 独立分量分析

独立分量分析(Independent Component Analysis，ICA)是假设在各个源信号之间独立[2-4]，并且观测信号的先验信息很少，仅仅通过获取的混叠信号实现源信号分离的一种盲源分离算法[5]。

ICA的数学模型可表达为x=AS，其中x=(x1,x2,…,xn)T表示n维向量，由混合矩阵A与原始向量S=(S1，S2，…，Sn)T进行线性混合而成。假设混合矩阵A与原始信号S都未知，通过统计观测信号x的特征，对原始信号S进行最大限度的逼近或者恢复，可以采用创建分离矩阵W的方法，对观测信号x进行分离变换后得到输出信号，此输出信号就是对源信号的最佳分解。图1为ICA基本模型：

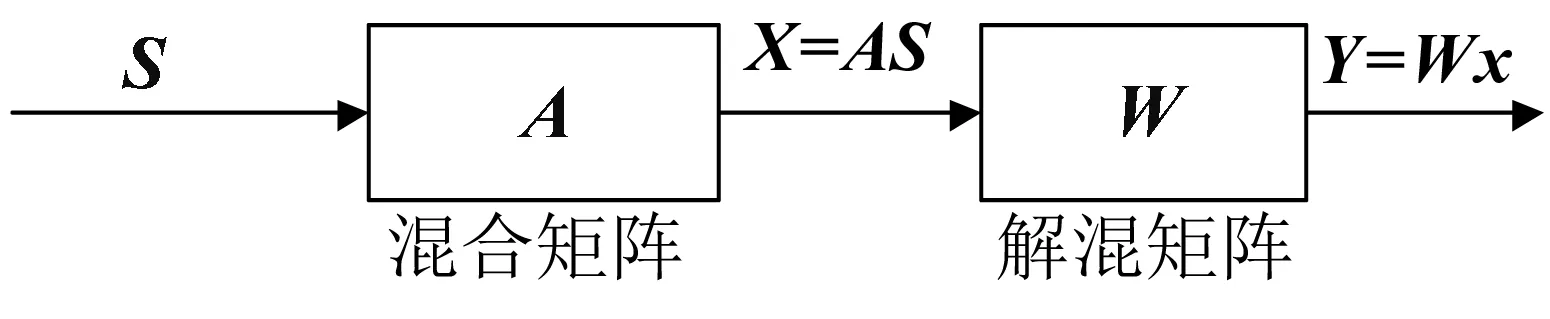
图1 ICA基本模型Fig.1 ICA basic model

Y=Wx

(1)

通过ICA进行信号的盲源分离主要包含两个部分[6-8]：一是独立性判断，二是优化算法。

本文主要采用FastICA算法。FastICA算法是一种ICA固定算法，其具有收敛速度快、计算简单等特点，常用于实际的信号处理，步骤如下：

1)对观测数据进行中心化处理；

2)选择具有单位范数的初始化变量；

3)更新初始化向量；

4)标准化处理。

(2)

式中：wk+1表示更新后单位向量，‖wk+1‖表示更新后向量模长。

进行上述步骤处理，就可以得到ICA算法中非分离矩阵W的行向量。在式(1)中加入分离矩阵W进行运算，就可以将原始信号s恢复。

2.2 基于最大信噪比盲源分离

基于最大信噪比(MAX-SNR)盲源分离是以信噪比函数为目标函数的全局优化算法。源信号S与其估计信号Y的误差e=S-Y表示噪声信号。信噪比函数为：

(3)

(4)

(5)

计算上式可以得到分离矩阵的解。

3 广义特征值盲源分离

利用常规的盲源分离方法进行源信号分离，如果源信号至少被重构一次，那么就认为源信号被有效分离。但是实际处理中，可能存在源信号被多次拷贝输出的问题，并且通过常规的盲源分离方法实现对源信号的真正分离，还要了解相关的信号处理技术，并明确源信号的数目。本文针对常规盲源分离在处理源信号中的劣势，提出一种新的盲源分离方法，即基于广义特征值的盲源分离算法。

通过上文描述可知，盲源分离的本质就是通过分离矩阵将源信号进行分离。如果分离矩阵W=A-1，则可认为源信号得到最优分解。通过盲源分离方法几乎不能得到源信号的先验知识。由上文知，逆变函数g可以决定盲源分离中分离矩阵的分离效果，因此本文采用有别于以往的逆变函数g，令：

(6)

式中：q表示参数。

分离得到的信号Y(t)，可表示为：

Y(t)=WX(t)

(7)

令：

g[S(t)]={g[s1(t)],g[s2(t)],…,g[(sN(t)]}T

(8)

g[S(t)]={g[x1(t)],g[x2(t)],…,g[xN(t)]}T

(9)

g[S(t)]={g[y1(t)],g[y2(t)],…,g[yN(t)]}T

(10)

由式(7)可以得到：

cov{g[X(t)]}=Acov{g[S(t)]}AT

(11)

cov{g[Y(t)]}=Wcov{g[X(t)]}WT

(12)

对于混合矩阵A，由于其是一个满秩矩阵，结合上式可知，cov{g[X(t)]}和cov[X(t)]是实对称正定矩阵，可以得到：

cov{g[X(t)]}w=λcov[X(t)]w

(13)

上式即为广义特征值问题。

根据研究可以知道，式(13)的解算结果中有N个特征值，从理论上讲源信号都可以被分解，因此总会存在一个行向量Wi使其满足WiAS(t)=kisi，并且cov{g[si(t)]}/cov[si(t)]为式(1)的特征值。

综上，基于广义特征值进行盲源分离的主要流程为：

1)将观测数据中心化；

2)构建新的逆变函数，计算g[X(t)]；

3)通过广义特征值函数W=eig{g[X(t)],X(t)}，对式(13)进行求解，得到分离矩阵；

4)计算Y(t)=WX(t)。按照前文所述，WX(t)中包含了源信号中所有的可分离信号。

4 试验验证

4.1 试验结果评价指标

使用统一的评价指标对混叠信号分离的结果进行评价，可以对不同分离算法的分离效果进行判断。一般使用二次残差和相关系数对盲源分离的结果进行评价。

4.1.1 二次残差

二次残差公式可表达为：

(14)

式中：E表示数学期望，VQM表示源信号与分离后信号的二次残差。一般来说，残差越小表示分离效果越好，但是通过式(14)对二次残差进行计算时需准确估计出信号的幅值，否则计算的结果将没有意义。因此，要对式(14)进行优化，表达式如下：

(15)

4.1.2 相似系数

相似系数的表达式如下所示：

(16)

图2 源信号波形Fig.2 Source signal waveform

4.2 仿真试验

本文首先通过仿真信号对基于广义特征值的盲源分离算法进行测试，并且同时通过MAX-SNR和ICA对仿真信号进行分离，对比三种信号处理效果。一组噪声与三组振动信号构成了仿真源信号，式(17)为正弦信号，式(18)为方波信号，式(19)为锯齿信号。

s1(t)=2sin(0.02πt)

(17)

s2(t)=2square(100t,50)

(18)

s3(t)=2[a，a，a，a，a，a，a，a]，a=linespace(-1，1，25)

(19)

随机噪声为一正态分布s4(t)N(0,0.05)，通过软件随机生成一混合矩阵A，利用混合矩阵与仿真源信号生成观测信号。其中混合矩阵：

(20)

图3为混合后的信号。利用三种方法对本文采用的仿真信号进行处理，图4、图5、图6分别是利用ICA、MAX-SNR及广义特征值分离得到的结果。从图中可以看出，基于广义特征值处理的结果最好，经算法进行分离后，信号的恢复效果都很好。通过计算信号分离前后之间的二次残差和相似系数，对分离效果进行评价，结果如表1和表2所示。

图3 混合后的信号Fig.3 The mixed signals

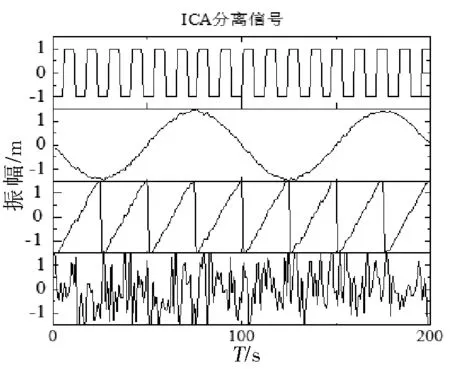
图4 经ICA分解后的信号Fig.4 The signals decomposed by ICA

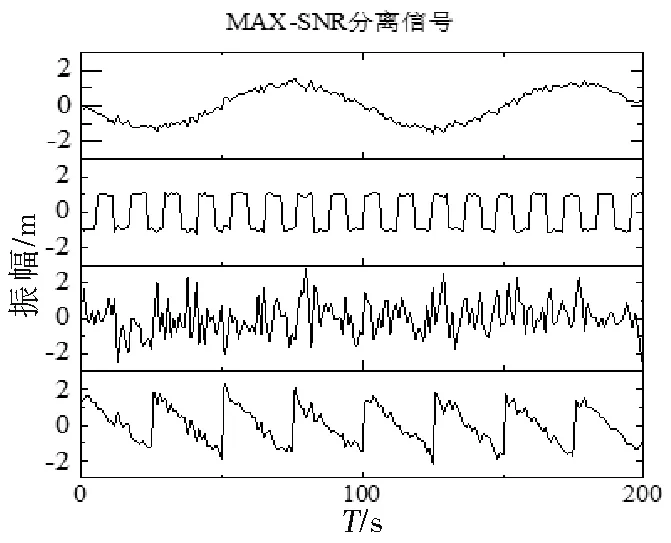
图5 经MAX-SNR分离后的信号Fig.5 The signals separated by MAX-SNR

图6 经本文提出算法分离后的信号Fig.6 The signals separated by the algorithm proposed in this paper

从表1和表2可以得出，三种盲源分离方法都可以对源信号进行有效分离，但是本文提出的算法分离源信号得到的效果比经ICA和MAX-SNR分离得到的效果好，该方法得到分离后的信号与源信号的相似系数较MAX-SNR分解的相似系数分别增加了8.0%、8.5%、10.7%，较ICA分解的相似系数分别增加了6.1%、5.9%、4.6%。

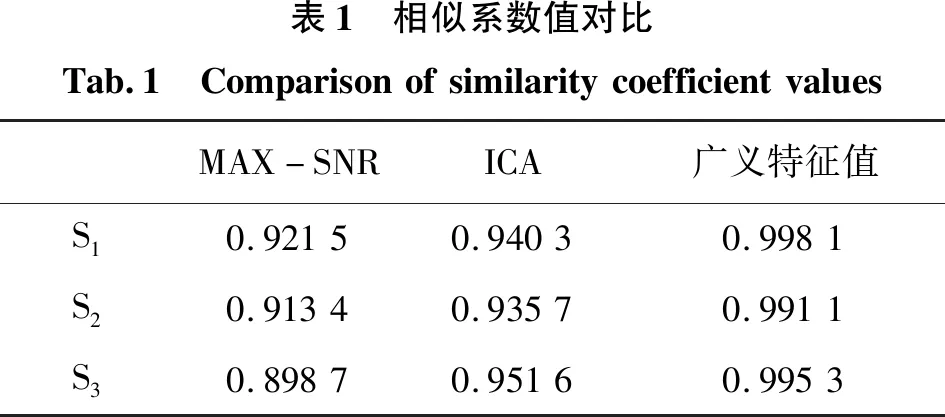
表1 相似系数值对比Tab.1 ComparisonofsimilaritycoefficientvaluesMAX-SNRICA广义特征值S10.92150.94030.9981S20.91340.93570.9911S30.89870.95160.9953

在二次残差的指标中，当二次残差值不大于-23dB时，则可认为算法进行信号分离得到的效果较好。广义特征值分离后的三种信号与源信号之间的残差较MAX-SNR分解的残差分别减少了28.7%、27.4%、29.8%，较ICA分解的残差分别减少了11.0%、7.9%、4.4%。结果表明，广义特征值分离算法较其他两种盲源分离算法在对源信号进行分离时有更好的效果。

表2 二次残差值对比Tab.2 ComparisonofsecondaryresidualsMAX-SNR/dBICA/dB广义特征值/dBS1-24.114-27.957-31.031S2-23.796-28.104-30.312S3-23.096-28.713-29.986

4.3 GNSS观测数据处理

为了得到广义特征值在GNSS变形监测数据中的分离效果，在仿真信号处理的基础上，在观测得到的GNSS监测数据中，截取第前200个历元多路径误差视为一路源信号，如图7所示，组成五路源信号。

图7 源信号Fig.7 The source signals

同样利用软件生成一混合矩阵，如式(21)所示，与源信号组成观测信号，如图8所示。

(21)

图8为混合信号。同样利用三种盲源分离方法对多路径误差源信号进行分离。图9、图10、图11分别是利用ICA、MAX-SNR及基于广义特征值分离得到的结果。从图中可以看出，广义特征值盲源分离算法分离效果最好，MAX-SNR分离算法分离的效果最差。为了对三种分离方法分离的效果进行更加客观的评价，分别计算信号分离效果的两种评价指标，结果如表3和表4所示。

图8 混合信号Fig.8 The mixed signals

图9 经ICA分离后的信号Fig.9 The signals separated by the ICA

图10 经MAX-SNR分解后的信号Fig.10 The signals decomposed by MAX-SNR

图11 本文提出算法分解后的信号Fig.11 The signals decomposed by the algorithm proposed in this paper

通过表3的相似系数可以看出，基于广义特征值分离信号的效果最好，本文提出的算法分离后的信号与源信号的相似系数较MAX-SNR分解的相似系数依次提高了1.9%、3.0%、3.4%、2.8%，较ICA分解的相似系数增加了1.0%、2.0%、2.4%、2.8%。在二次残差这一评价指标中，利用三种方法分离观测信号后计算得到的二次残差都小于-23dB。

广义特征值分离后的信号与源信号之间的残差较MAX-SNR分解的残差分别减少了21.8%、19.5%、18.4%、19.3%，较ICA分解的残差分别减少了15.5%、11.0%、11.4%、11.6%。

通过表格对比描述可知，在增加GNSS多路径误差后，利用本文提出的广义特征值盲源分离仍然可以得到很好的效果，对于GNSS变形监测误差模型建立有很高的参考价值。

表3 相似系数对比Tab.3 Comparisonofsimilaritycoefficient信号MAX-SNR/dBICA/dB广义特征值/dBS10.98120.99011.0000S20.96940.97930.9989S30.96130.97050.9939S40.97050.96980.9974

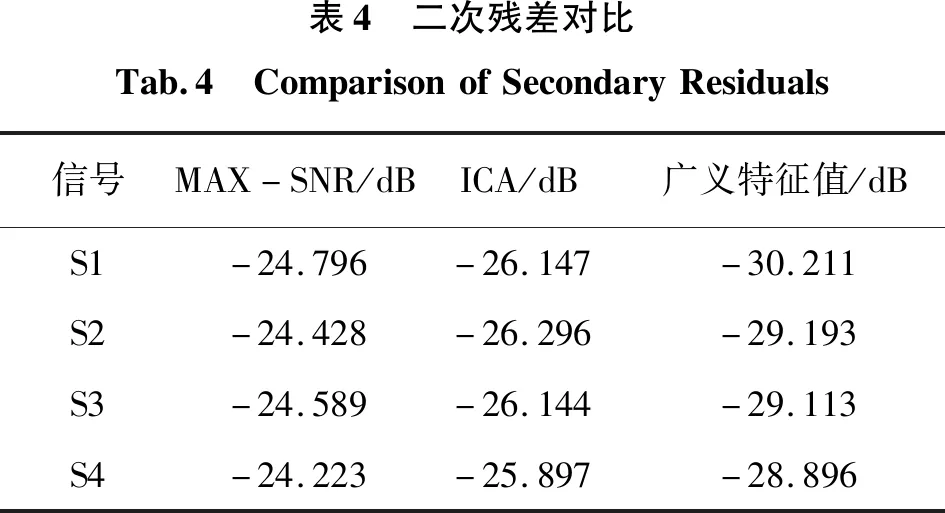
表4 二次残差对比Tab.4 ComparisonofSecondaryResiduals信号MAX-SNR/dBICA/dB广义特征值/dBS1-24.796-26.147-30.211S2-24.428-26.296-29.193S3-24.589-26.144-29.113S4-24.223-25.897-28.896