基于SINS/TAN/ADS/MCP的无人机组合导航系统

汤郡郡，胡 伟，刘祥水，尹进军，宋中建

（国营芜湖机械厂，芜湖 241007）

无人机武器系统是未来空中战场的主力装备，然而，战场形势瞬息万变，具备快速反应、高机动性能、目标捕获能力以及协同作战、精确打击的作战模式是无人机发展的必然方向。为了保证生存能力和命中率，无人机必须能够快速起飞，准确进入作战区域和返还基地，这就要求无人机导航系统必须同时具备自主可靠、高精度、能快速定位的能力[1]。

捷联惯性导航系统（Strapdown Inertial Navigation System, SINS）仅依靠自身就能在全天候条件下，在全球范围内进行连续的导航和定位，它自主、隐蔽，能获取载体完备的运动信息，但是其定位误差会随着时间的积累不断增大；地形辅助导航系统（Terrain Aided Navigation, TAN）是一种利用地形高程特征来进行辅助定位的方法，它自主、隐蔽、连续、全天候，导航定位误差不随时间积累，但它需要有先验的地形图且依赖其它导航系统的位置输出[2]；大气数据系统（Air Data System, ADS）利用安装在机体上的大气传感器提供的压力、温度等信息解算载体的空速、大气高度等信息，不需要依赖外部条件，它可靠性高，不受高度、地形等因素的影响，是一种较为理想的辅助导航设备；电子磁罗盘（Magnetic Compass, MCP）能够提供航向信息，且其输出的导航信息误差不随时间的增长而增长，适合长时间高精度导航，但是电子磁罗盘受外界影响较大，精度也不易提高。

上述几种导航方式都存在着一些自身难以克服的缺点，将多种导航方式进行融合，不仅可以取长补短提高导航精度，还可以适当降低对单一导航系统的要求，提高系统的可靠性和容错性能，满足无人机导航系统的高要求[3]。本文所述无人机组合导航系统总体方案如图1所示。

图1 UAV组合导航系统总体方案Fig.1 UAV integrated navigation system

1 SINS/TAN系统数学模型

SINS系统利用惯性器件（陀螺仪、加速度计）测量出载体的角速度和线加速度，经过积分和各种算法得到载体的位置、速度及姿态信息。

1.1 SINS误差模型

选取东北天坐标系为导航坐标系，载体坐标系x轴沿机体横轴指向右，y轴沿机体纵轴指向前，z轴垂直于x轴和y轴所确定的平面构成右手坐标系。选择位置误差、速度误差、姿态误差、陀螺漂移和加速度计偏置作为状态量：

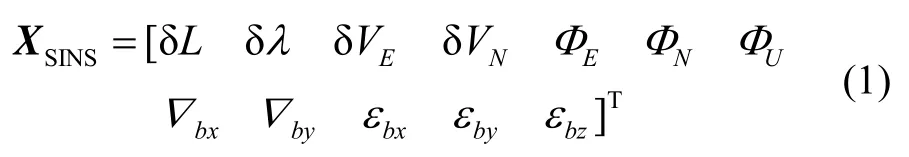
其中：δL、δλ分别是纬度、经度误差；δVE、δVN分别是东向、北向速度误差；EΦ、NΦ、UΦ分别是东向、北向、天向失准角；∇bx、∇by分别是x、y轴向的加速度计偏置；εbx、εby、εbz分别是x、y、z轴向的陀螺漂移；

系统状态方程为

其中：

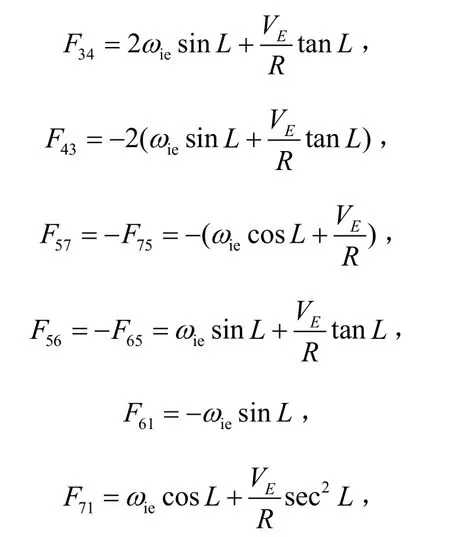
Cij为姿态转移矩阵中的元素。

1.2 SINS/TAN状态方程及观测方程

由参考文献[10]可知，SINS/TAN系统的状态方程就是SINS的状态方程，系统观测量由SINS输出的位置信息LSINS、λSINS减去TAN输出的位置信息LTAN、形成，观测方程可由下式表示：

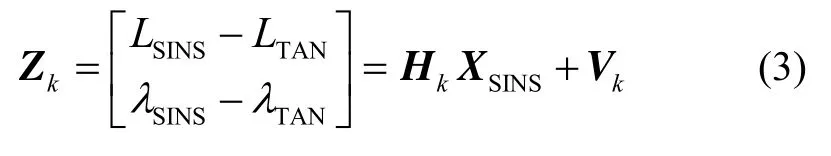
其中：Vk为TAN子系统的观测噪声；

2 SINS/ADS系统数学模型

利用安装在载体外侧的压力传感器、总温传感器和攻角传感器测量载体周围流场的动压、静压、总温和攻角，并将这些信息送到计算机中进行解算，得到载体的气压高度和速度等导航信息。

2.1 ADS误差模型

由大气数据系统测量得到的静压值计算出的海拔高度，可直接提供给TAN使用。将大气数据系统的速度误差均建模为一阶马尔可夫过程：

2.2 SINS/ADS状态方程及观测方程

状态方程为：

观测方程为：

3 SINS/MCP系统数学模型

磁航向测量的误差是由很多因素造成的，具体可以分为两类：第一类是系统自身存在的误差，包括制造误差、安装误差，主要会对三轴磁阻传感器的输出信号产生影响；第二类误差是由电子磁罗盘周围环境因素而造成的误差，主要指罗差。

3.1 MCP误差模型

使用电子磁罗盘必须经过严格的误差补偿。经过误差补偿以后，电子磁罗盘的误差可近似为一阶马尔可夫过程：

其中：τMCP、wMCP分别是一阶马尔可夫过程的相关时间和驱动白噪声。

3.2 SINS/MCP状态方程及观测方程

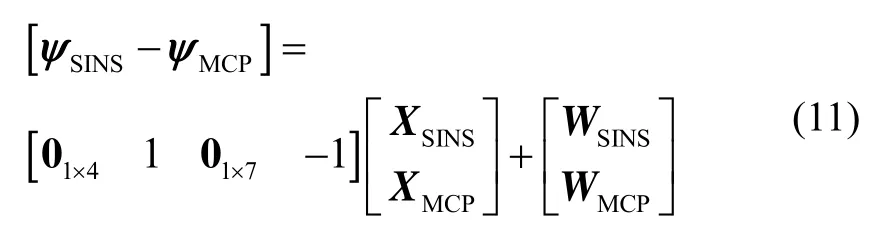
状态方程为：

观测方程为：

4 组合导航系统设计

4.1 系统设计思想

系统设计框图如图2所示，其中：SINS为公共系统，提供位置、速度和姿态各项信息；SINS与 TAN构成位置局部滤波器，实现位置信息的综合；SINS与ADS构成速度局部滤波器，实现速度信息的综合；SINS与MCP构成航向局部滤波器，实现航向信息的综合。

图2 滤波器设计结构图Fig.2 Design structure of filter

3个局部滤波器均为卡尔曼滤波器，它们输出的数据送入全局滤波器进行融合。全局滤波器输出的数据不直接反馈给各局部滤波器，因此不同局部滤波器之间不存在信息交流，某个局部滤波器故障不会影响另外的滤波器，所以整个系统具有很好的容错性，可以满足无人机导航系统高精度高可靠性的要求。

4.2 联邦卡尔曼滤波器算法

1）局部滤波器算法

时间更新算法：

量测更新算法：

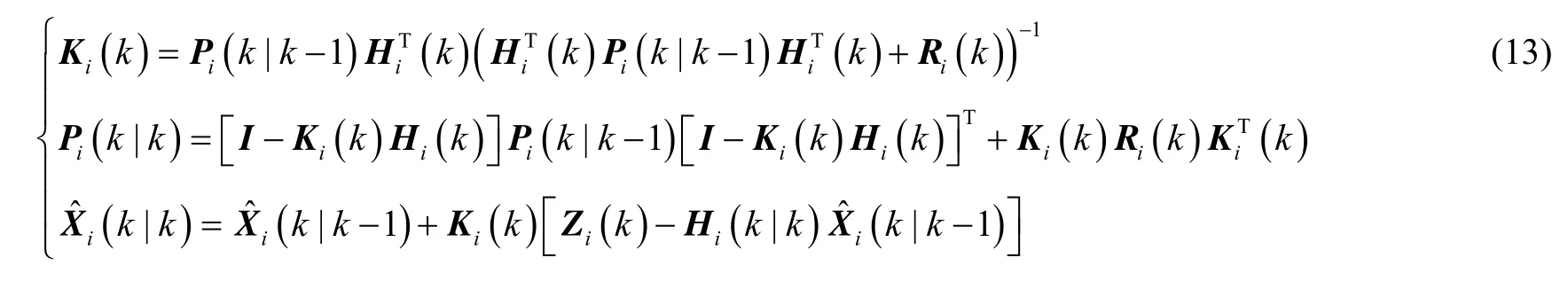
2）全局滤波器算法

全局滤波器不进行滤波处理，只是将各个局部滤波器的估计值按式(14)进行融合，得到全局最优估计值和最优估计方差阵：

3）信息分配

联邦滤波中的信息分配原则如下：

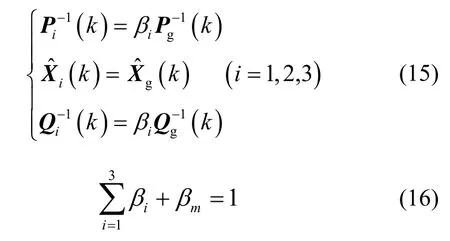
式中：iβ为局部滤波器信息分配因子；mβ为全局滤波器信息分配因子，本文选择融合重置模式下的联邦滤波，有

联邦滤波器可以获得与卡尔曼滤波器相当的估计精度，同时具有计算量小、容错性强等优点，而影响性能的关键是分配系数的选择。由于各局部滤波器的估计精度高低可以通过估计误差协方差矩阵来反应，所以考虑根据估计误差协方差矩阵的特征值来确定分配系数，有：

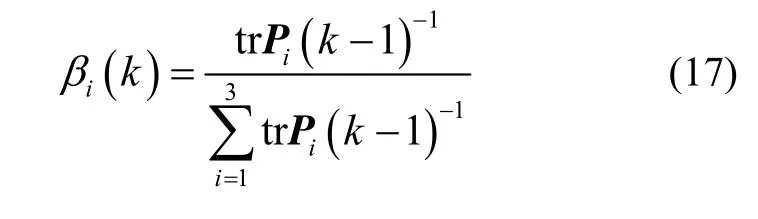
5 仿真分析

仿真条件及参数设置如下：

UAV初始位置：北纬38°，东经120°；SINS初始误差：纬度 5″，经度 5″；东、北、天三向速度误差0.1 m/s；航向偏差0.5′；加速度计零偏和随机漂移20 μg；陀螺常值漂移和随机漂移0.1 (°)/h；TAN位置误差：50 m；ADS速度误差：1.2 m/s；电子磁罗盘精度 1.5°。

如图3所示，从上到下分别为SINS/ADS、SINS/MCP、SINS/TAN局部滤波器以及 SINS/TAN/ADS/MCP联邦滤波器位置误差曲线。

如图4所示，从上到下分别为SINS/ADS、SINS/MCP、SINS/TAN局部滤波器以及 SINS/TAN/ADS/MCP联邦滤波器速度误差曲线。

图3 位置误差曲线Fig.3 Curves of positioning errors

图4 速度误差曲线Fig.4 Curves of speed errors

图5所示分别为SINS/ADS、SINS/MCP、SINS/TAN局部滤波器以及SINS/TAN/ADS/MCP联邦滤波器航向误差曲线。

图5 航向误差曲线Fig.5 Curves of heading errors

将各局部滤波器估计误差与全局滤波器估计误差进行分析比较，结果如表1所示。

从上述分析结果可以看出，SINS/ADS速度局部滤波器，由于速度信息得到修正，所以速度误差较小而位置误差和航向误差较大；SINS/MCP航向局部滤波器，航向误差较小，但位置和速度误差的估计精度不理想；SINS/TAN位置局部滤波器，位置误差较小，但航向和速度精度不高；相较而言，SINS/TAN/ADS/ MCP全局滤波器在位置、速度、航向上均具有较高的估计精度，可以满足无人机导航系统高精度、高可靠性的要求。

表1 仿真结果分析比较Tab.1 Comparison on simulation results

6 结 论

本文提出的无人机导航系统是结合捷联惯性导航系统、地形辅助导航系统、大气数据系统以及磁罗经导航的组合导航系统。采用联邦卡尔曼滤波方式对导航信息进行融合，扬长避短。对比仿真实验结果可以看出：SINS/TAN系统位置误差较小，但航向误差较大；SINS/ADS系统速度误差较小且比较稳定，但位置误差随时间发散；SINS/MCP系统航向误差方差可达 0.3783′，但其位置和速度估计精度不理想；而该组合导航系统可以同时获得较高的位置、速度以及航向精度，对于实现UAV高精度高可靠性导航具有重要的意义。

参考文献（References）：

[1]方铮. 长航无人机多源信息融合自主导航及其仿真关键技术研究[D]. 南京: 南京航空航天大学, 2014.Fang Z. Research on Autonomous navigation with multi-source information fusion of long-endurance UAV[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014.

[2]徐晓苏, 汤郡郡, 张涛, 等. 一种结合地形和环境特征的水下导航定位方法[J]. 中国惯性技术学报, 2015,23(5): 590-596.Xu X S, Tang J J, Zhang T, et al. Under- water navigation method based on terrain and environmental features[J].Journal of Chinese Inertial Technology, 2015, 23(5):590-596.

[3]Jiang D N, Mekonnen T M. INS/GPS/MNS Integrated navigation system with federated Kalman filtering[J].Advanced Materials Research, 2013, 718-720: 1207-1212.

[4]Xu T L. Research on federated Kalman filter for navigation system[C]//Proceeding of 2011 Third Pacific-Asia Conference on Circuits, Communications and System.2011: 1-4.

[5] 张科, 刘海鹏, 李恒年, 等. SINS/ GPS/CNS组合导航联邦滤波算法[J]. 中国惯性技术学报, 2013, 21(2):226-230.Zhang K, Liu H P, Li H N, et al. SINS/GPS/CNS integrated navigation federal filtering algorithm[J].Journal of Chinese Inertial Technology, 2013, 21(2):226-230.

[6]Yang S J. Stellar refraction-based SINS/ CNS integrated navigation system for aerospace vehicles[J]. Journal of Aerospace Engineering, 2016, 29(2): 1-11.

[7]Deng H, Liu G B, Chen H M, et al. The Application of federated Kalman filtering in SINS/GPS/CNS integrated navigation system[C]//International Journal of Wireless and Microwave Technologies, 2012(2): 12-19.

[8]李佩娟, 徐晓苏, 张涛. 信息融合技术在水下组合导航系统中的应用[J]. 中国惯性技术学报, 2009, 17(3):344-349.Li P J, Xu X S, Zhang T. Application of information fusion to integrated navigation system of underwater vehicle[J]. Journal of Chinese Inertial Technology, 2009,17(3): 344-349.

[9]Gao S S, Xue L, Zhang Y M, et al. Random weighting method for estimation of error characteristics in SINS/GPS/SAR integrated navigation system[J]. Aerospace Science and Technology, 2015, 46: 22-29.

[10]陈燕丽. SINS/TAN/GPS组合导航信息融合技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.Cheng Y L. Research on information fusion technology of SINS/TAN/GPS integration navigation system[D].Harbin : Harbin Engineering University, 2011.

[11]孟阳, 高社生, 高兵兵, 等. 基于 UKF的 INS/GNSS/CNS组合导航最优数据融合方法[J]. 中国惯性技术学报, 2016, 24(6): 746-751.Meng Y, Gao S S, Gao B B, et al. UKF-based optimal data fusion method for integrated INS/GNSS/CNS[J]. Journal of Chinese Inertial Technology, 2016, 24(6): 746-751.