GNSS接收机中一种自适应比特同步的新颖算法
2018-05-10袁建国陈忠平林金朝
袁建国,王 姣,陈忠平,庞 宇,林金朝
(重庆邮电大学 光电信息感测与传输技术重庆市重点实验室,重庆 400065)
在 GNSS接收机设计中,跟踪的长时间相干积分,导航电文的提取以及伪距的测量都需要在比特同步的基础上完成[1]。GPS C/A码的码周期为1 ms,导航电文的数据率为50 bit/s,即1 bit的导航电文调制了20个周期的C/A码,这就造成了比特翻转边界的不确定性[2]。高灵敏GNSS接收机的信号跟踪设计都会使用相干积分,而如果在相干积分的这段时间内存在比特翻转,则会造成信噪比的损失,进而使得跟踪信号的灵敏度降低[3-4]。比特边界的误判会增大比特判决出错的概率,使得误码率增加进而影响导航电文的提取。产生伪距测量值基本上等价于确定接收信号的发射时间,而信号的发射时间信息有一部分隐含在接收到的导航电文数据比特中,因此伪距的计算也需要用到比特边界[5]。现今,高动态接收机的研究工作越来越受到人们的关注,其对快速定位有很高的要求,快速的比特同步能够减少接收机的同步时间,进而降低首次定位时间[6]。因此,如何快速地完成比特同步具有重要的研究意义。
目前消费级接收机主要采用的是Parkinson[7]等人提出的直方图法来进行比特同步。该方法将载波环输出的1 ms导航数据比特用1~20循环编号,逐个统计相邻2 ms数据的符号跳变情况,若发生跳变则计数器加 1,反之计数器值保持不变。经过一段时间的统计后,如果某一位置的直方图计数器值明显高于其他位置,则判定该位置为比特边沿所在位置。该方法的实质是对相关器输出的符号进行硬判决,其只利用了比特翻转相邻边界的两个C/A码周期的能量,没有用到全部20个周期的能量,这就导致其在低信噪比时同步性能差,因此该方法在弱信号条件下并不适用[8]。Kokkonen[9]等人将最大似然方法(Maximum likelihood,ML)引入了比特同步。该方法把20个候选位置之后的连续20个数据进行累积得到相应的比特能量,再经过非相干累加,然后找到对应20个位置中比特能量最大值所在的位置作为比特边界。该方法可以通过增加非相干累加次数来提高信噪比,使得在弱信号时仍有较好的位同步性能。Sharfer I[10]以及Sahmoudi M[11]等人对最大似然法的比特同步的具体实现进行了简化。Ren T[12]等在考虑了积分时间和多普勒频偏的情况下对最大似然比特同步的应用进行了进一步的分析。
实际应用中,ML法为了保证弱信号的正确同步概率,通常固定一个比较大非相干累加次数[8,13]。但对于强信号来讲,非相干累加次数较大会使平均估计时间变长,进而导致首次定位时间增加。针对这一缺陷。本文提出了一种以比特能量最大值为门限的自适应比特同步算法,利用比特能量最大值为检测量,根据信号强度自适应地调整非相干累加次数,使得接收机在保证一定的正确同步概率时,达到有效地降低比特同步时间的目的。仿真结果表明,正确选择阈值后,当信号强度大于-145 dBm时,与固定200次非相干累加的传统最大似然比特同步算法相比,本算法可以节省85%的比特同步时间。
1 传统的最大似然算法
1.1 信号模型
假设GNSS信号的数据比特周期Tb和测距码周期之间的比值为M,即在这种情况下,通过单个码周期计算且采样率为1/Tc的长度为N的数据序列在K时刻的相关器输出为[13]
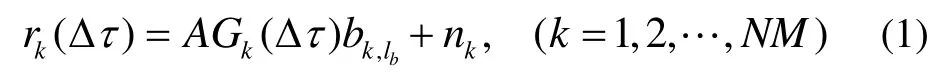

对于某个导航数据比特候选位置δ,δ∈{0,1,2,… ,1 9},有等式(3)成立:

1.2 最大似然比特同步算法
对于一个包含N个接收信号样本的矢量而言,由正态分布的概率密度函数可以求得其对应的似然函数为各个样本似然函数的乘积,如式(4)所示[14]:

最大似然法实现导航数据比特同步的过程就是在参量δ、A、b意义下最大化似然函数L。式(4)中求和项的第一部分与参数的选取无关可以忽略,去掉第一部分后式(4)中的求和可以表示为这样的形式,因此求最大似然函数L相当于求最大值

显然,式(5)的函数取最大值时bk总是与的符号相同,因此导航数据比特边界位置的确定可以从导航数据比特值的检测中分离出来,又所以式(5)可以改写成:

由于接收信号对导航数据比特进行了调制,所以估计过程将产生±1的偏差,又由于式(6)是对绝对值求和,因此对估计结果并没有影响。通过最大化式(7)来获得导航数据比特边界的估计值

式(7)反映了相应积分时间的比特能量,因此称其为比特能量观测量。
传统的最大似然算法完成比特同步的具体步骤大致如下:1)导航数据经过1 ms相干积分后的输出信号;2)对每 20 ms内的输出信号进行滑动求和得到20组M个积分累加值3)对每组观测量取绝对值后分别做M次非相干累加获得20个观测量;4)找到20个观测量中的最大值,最大值所在的位置即为导航数据比特边界位置。该方法相对于直方图而言,是在进行了M次非相干累加后再进行的比特边界判决,因此可以适用于弱信号条件并且具有更好的正确同步概率性能。
传统的最大似然算法在完成比特同步时通常采用一个较大的固定非相干累加次数,比如200次,以提高弱信号条件下的正确同步概率。但对于强信号而言,并不需要进行这么多次的非相干累加。接下来通过枚举式仿真验证了这一点,具体的仿真结果如图1所示。

图1 ML法在不同非相干累加次数下的正确同步概率Fig.1 Correct synchronization probability of ML method under different incoherent accumulation times
由图1可知,在信号强度达到-140 dBm以上时,10次左右的非相干累加次数就可以使正确同步概率达到90%以上,并且20次和50次的非相干累加时的正确同步概率曲线基本接近,只有很小的差距。但多余的非相干累加次数极大的增大了比特同步的平均估计时间(Mean Estimation Time, MET),使得首次定位时间延长。
2 自适应比特同步算法
本文针对传统最大似然算法在强信号时使用了多余的非相干累加次数这一缺陷,提出了一种自适应比特同步算法。该方法针对不同的信号强度来自适应地调整非相干累加次数,可以在保证一定的正确同步概率时,避免不必要的非相干累加次数,使得平均估计时间明显减少,从而达到较快的首次定位的目的。
当没有非相干累加时,比特能量观测量为

式中:P为信号功率;φ为正确的比特边界。若相邻的两个数据比特存在符号跳变,可设,则式(8)可改写为

从式(9)可以推论,相邻的数据比特没有比特跳变或者相干累加的起始边沿与比特边界重合,即δ=φ时,比特能量观测量Sm,δ具有最大值。直接通过理论计算根据信号强度估算出非相干累加次数比较困难,因此我们通过大量的仿真分析来得到二者的关系。图2为蒙特卡洛数值仿真结果。

图2 比特能量最大值与信号强度和非相干累加次数的关系Fig.2 The relationship between the maximum bit energy, the signal intensity and the incoherent accumulation times
由图2可知:在某个固定的非相干累加次数下,在信号强度为-150 dBm以上时,比特能量最大值随着信号强度的增大近似的呈单调递增的关系,并且随着信号强度增大到一定程度后比特能量最大值基本保持不变;在某个特定的信号强度时,非相干累加次数越大,其对应的比特能量最大值越大。根据这些特点,我们可以为比特能量最大值设一个门限值,使其达到该门限值后就停止非相干累加,然后进行比特边界的判决。另外,考虑到输入数据出错时,一直执行非相干累加仍达不到预设的门限值而陷入死循环的情况,给非相干累加次数设定了一个上限值 200,使得当非相干累加次数达到200时,无论此刻比特能量最大值是否达到门限值都停止执行非相干累加,并进行比特翻转边界判决。具体方案为:1)实时地输入1 ms相干积分后的导航数据比特;2)对每20 ms的数据比特进行滑动求和得到20组相干积分累加值;3)执行一次非相干累加;4)排序法找到比特能量最大值;5)与预设门限进行比较,如果该最大值超过所设的阈值则停止进行非相干累加,判决此时的比特能量最大值所在的位置即为比特边界;6)如果该最大值小于阈值则对紧接着输入的数据重复执行步骤1至步骤5,直至超过阈值或非相干累加次数达到200;7)如果该最大值小于阈值且此时非相干累加次数已经达到 200,则停止非相干累加进行比特边界的判决,并认为此时比特能量最大值所在的位置就是比特边界。实现的具体流程如图3所示。
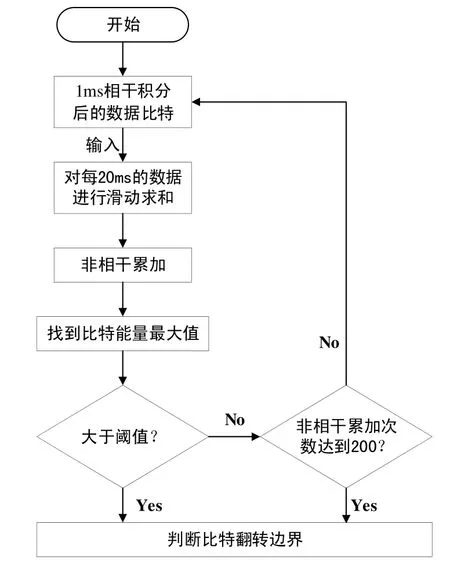
图3 自适应比特同步算法流程图Fig.3 Flow chart of adaptive bit synchronization algorithm
3 仿真测试与分析
3.1 仿真测试方案
通过统计仿真方法对本文方法的性能进行仿真分析并与传统的最大似然比特同步算法进行比较。信号模型由式(1)给出。仿真采用MATLAB生成GPS 19号卫星数据,仿真参数为:采样频率16.368 MHz,系统中频4.092 MHz。在原始信号中预设比特边界为20,然后使其边界逐个移动,使得比特边界在 20~1之间变化。当比特同步完成后找到的比特边界与预设的比特边界相同时,就判定此时比特同步估计正确。对信号强度为-153 dBm至-135 dBm的信号随机进行了蒙特卡洛仿真,统计了比特同步估计正确的次数,获得正确同步概率。统计每次正确估计的非相干累加次数,并计算其均值,从而得到平均估计时间MET:
(MET=非相干累加次数×导航数据比特周期)。
3.2 仿真结果分析
图4给出了不同门限下的正确同步概率性能;图5是信号强度为-148 dBm至-141 dBm的局部放大,小图为信号强度为-145 dBm至-135 dBm纵轴的进一步放大。图4~5中五角星标记的紫色曲线为200次的固定非相干累加次数的传统最大似然仿真结果。

图4 正确同步概率的性能比较(104次仿真)Fig.4 Comparison of correct synchronization probability performances (104 times of simulations)

图5 正确同步概率的性能比较(局部放大)Fig.5 Comparison of correct synchronization probability performances (partial magnification)
可见,当门限大于一定值时(如 1.5×108),改进后的方法的正确同步概率曲线与传统的最大似然比特同步方法基本重合,差距在5%左右。
图6给出不同门限下的平均估计时间。对照传统的最大似然比特同步方法使用固定的非相干累加 200次,其平均估计时间为200×0.02 s=4 s(图中未画出)。而本文提出的改进方法随着信号强度的增大其平均估计时间逐渐降低,其中,信号强度大于-145 dBm后达到稳态值。门限值为 1.5×108时,平均估计时间小于0.6 s,相对于传统算法的200次非相干累加,节省了约85%的比特同步估计时间。

图6 不同门限下的平均估计时间性能比较(104次仿真)Fig.6 Comparison of mean estimated time performances under different thresholds(104 simulation)
由图5~6可知,比特能量最大值门限的选取对比特同步的性能有较大的影响。门限值选取过低会导致正确同步概率降低,但是过高的门限值并不会使正确同步概率进一步增大反而会增加平均估计时间,使得首次定位时间延长。由图5~6可推论,通过枚举法发现当门限值取 1.5×108时,能够在保证一定的正确同步概率下大大降低平均估计时间,因此本文提出的改进方法在具体应用时门限值应设为1.5×108。
4 总 结
本文在对传统的最大似然比特同步算法进行了详细分析后,提出了一种改进后的自适应比特同步算法。该方法利用了比特能量最大值、信号强度和非相干累加次数三者之间的关系,引入了比特能量最大值作为检测量,以达到针对不同信号强度自适应的调整非相干累加次数的目的,并且在具体的实现方案时考虑到了数据出错的情况,给非相干累加次数设定了一个上限值 200,避免了数据出错时一直非相干累加仍达不到预设的比特能量最大值门限值而陷入死循环的情况。仿真测试结果表明,本文提出的改进方法在保证了正确同步概率基本不变的前提下,极大地缩短了找到比特边沿的平均估计时间,满足了高动态导航接收机快速完成同步,进而降低首次定位时间的要求。
参考文献(References):
[1]Yu H, Liu Y J. Research on bit synchronization based on GNSS[C]//International Conference on Materials Science,Energy Technology, AIP Publishing LLC, 2017: 522-526.
[2]Li X, Guo W. Efficient differential coherent accumulation algorithm for weak GPS signal bit synchronization[J].IEEE Communications Letters, 2013, 17(5): 936-939.
[3]袁建国, 欧松林. GPS接收机并行捕获算法的研究[J].重庆邮电大学学报(自然科学版), 2013, 25(4): 470-474.Yuan J G, Ou S L. Study on parallel acquisition algorithm for GPS receiver[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition,2013, 25(4): 470-474.
[4]袁建国, 欧松林, 刘飞龙, 等. 一种适用于微弱信号的新颖双峰值比率捕获策略[J]. 中国惯性技术学报, 2015,23(1): 98-102.Yuan J G, Ou S L, Liu F L, et al. Novel double-peakvalue ratio acquisition strategy for weak signal[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 98-102.
[5]谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2015: 324-328.Xie G. Principles of GPS and receiver design[M]. Beijing:Publishing House of Electronics Industry, 2015: 324-328.
[6]靖守让, 李柏渝, 刘文祥, 等. 地球静止轨道粗定位的北斗系统接收机快速定位方法[J]. 国防科技大学学报,2015, 37(4): 77-81.Jing S R, Li B Y, Liu W X, et al. A quick location method for BDS receiver based on coarse positioning by GEO constellation[J]. Journal of National University of Defense Technology, 2015, 37(4): 77-81.
[7]Parkinson B W, Spillker J J. Global positioning system:theory and application[M]. American Institute of Aeronautics and Astronautics, Inc., 1996.
[8] 郑睿, 陈培, 陈陌寒, 等. 一种自适应最大似然GPS比特同步方法[J]. 系统仿真学报, 2009, 21(24): 7747-7750.Zheng R, Chen P, Chen M H, et al. Self-adaptive maximum likelihood method for GPS bit synchronization[J]. Journal of System Simulation, 2009, 21(24):7747-7750.
[9]Kokkonen M, Pietila S. A new bit synchronization method for a GPS receiver[C]//IEEE/ION Position Location and Navigation Symposium. 2002: 85-90.
[10]Sharfer I, Hero A O. Spread spectrum sequence estimation and bit synchronization using an EM-type algorithm[C]//International Conference on Acoustics, Speech,and Signal Processing. 2002: 1864-1867.
[11]Sahmoudi M, Amin M G. A maximum-likelihood synchronization scheme for GPS positioning in multipath,interference, and weak signal environments[C]//IEEE 64th Vehicular Technology Conference. 2006: 1-5.
[12]Ren T, Petovello M, Basnayake C. Requirements analysis for bit synchronization and decoding in a standalone high-sensitivity GNSS receiver[C]//International Conference on Ubiquitous Positioning Indoor Navigation and Location Based Service. Helsinki, Finland, 2013: 1-9.
[13]Qi J Z, Song P. Research on the bit synchronization algorithm and multiplexing technology in GNSS receiver[J]. China Communications, 2014, 11(14): 30-36.
[14]Ren T, Petovello M. An analysis of maximum likelihood estimation method for bit synchronization and decoding of GPS L1 C/A signals[J]. Eurasip Journal on Advances in Signal Processing, 2014(1): 3-14.
