基于JADE盲源分离算法的雷达信号研究

王瑜，李小波，毛云翔，黄超

(电子工程学院，安徽 合肥 230037)

基于JADE盲源分离算法的雷达信号研究

王瑜，李小波，毛云翔，黄超

(电子工程学院，安徽 合肥 230037)

盲源信号分离技术在雷达抗干扰领域得到了广泛的关注和应用研究，所以对经过盲源分离的雷达信号的研究是至关重要的。分析了经过盲源分离的雷达信号存在幅度、相位的不确定性，并通过仿真分析得出了信噪比对盲源分离的影响。仿真结果表明，在信噪比满足一定的条件下，盲源分离能从强压制干扰中将信号分离。

雷达抗干扰；盲源分离；信噪比；雷达信号；幅度；相位

0 引言

盲源信号分离(blind source separation，BSS)是现代雷达信号处理技术的前沿领域之一[1-4]，通过观测到的混合接收信号并在先验知识较少的前提下，利用信号间的独立统计特性[5-8]将混合信号分离开，提取出有用的回波信号。这一技术在雷达抗干扰中得到了广泛的研究与应用，文献[9-10]研究了盲源分离抗欺骗干扰的方法，该方法能有效从欺骗干扰中实现信号的分离，在对抗有源压制干扰(噪声调频)的研究中盲源分离技术扮演着重要的角色[11-14]，然而对于盲源分离后的雷达信号幅度、相位特性以及盲源分离算法性能与信噪比的关系并没有研究。

本文研究了经过盲源分离的雷达信号存在幅度、相位和顺序的不确定性，并通过仿真分析得出信噪比对盲源分离信号的影响，得出了盲源分离实现雷达主瓣抗干扰时必须满足一定的信噪比，本文通过仿真得出，当信噪比不小于10 dB条件下，盲源分离对信号和干扰的分离效果最好。

1 问题描述和信号模型

1.1 问题描述

盲源分离技术应用于雷达主瓣抗干扰的技术研究中，本文提出了一种基于矩阵联合对角化特征矢量的盲源分离抗主瓣干扰算法，其算法具体工作过程如图1所示。

图1 问题描述Fig.1 Problem description

1.2 信号模型

图2所示为特征矩阵联合近似对角化(joint approximate diagonalization of eigen matrices,JADE)盲源分离抗主瓣干扰的信号模型，在加性噪声n(k)，接收目标和干扰信号数目总M和不大于接收通道的数目N，即M≤N，同时目标和干扰在方向上存在差异，接收的目标和压制干扰信号之间相互统计独立。接收的混合信号的数字化模型表示为

r(k)=Hs(k)+n(k),

(1)

式中：k为采样时刻；r(k)=(r1(k),r2(k),…,rN(k))T；H为N×M维混合矩阵，H=(h1,h2,…,hM)， 由M个N维列向量组成；s(k)=(s1(k)，s2(k), …,sM(k))T， 那么n(k)=(n1(k),n2(k),…,nN(k))T。

图2 信号模型Fig.2 Signal model

2 JADE盲源分离

2.1 JADE算法流程

JADE算法是先对观测数据白化，然后求其四阶累积量矩阵，并对其进行特征值分解，求得混合矩阵的近似。该算法的流程如下：

(2)

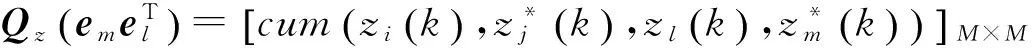
(3)

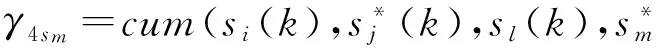
UΓklUH.

(4)

基于以上分析，可以由酉矩阵U的估计矩阵V得到观测数据的盲源分离结果为

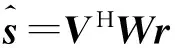
(5)

2.2 信号模糊性

考虑雷达接收数据的信号模型为

r=Hs+n，

(6)

(7)

r=Hs+n=(HP)(PTs)+n.

(8)

显然，s与PTs所包含的统计信息等价，故盲源分离算法在根本上无法消除顺序不确定性。源信号的信息主要包含在信号的波形中，盲源分离信号的顺序不确定性，并不影响对源信号的估计。

仅仅考虑幅值和相位不确定。Λ对角阵中元素的增大或减小以及正负符号的改变，对应的源信号幅度变化以及信号正负的变化，在雷达信号中体现为信号幅度和相位的不确定性。重写式(6)为

r=Hs+n=(HΛ)(Λ-1s)+n.

(9)

显然，s与Λ-1s所包含的统计信息等价，故盲源分离算法在根本上无法消除幅值和相位不确定性。

运用盲源分离技术实现雷达主瓣抗干扰，主要是利用了目标信号与干扰信号的统计独立特性，将目标信号和干扰信号分离，实现抗干扰的目的。由上述分析可知，盲源分离信号存在模糊性，但不影响信号间的统计独立性。

3 盲源分离算法性能分析

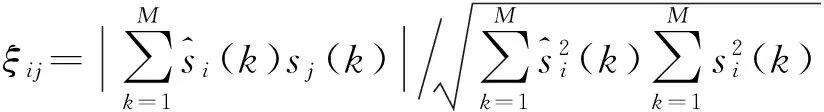
(10)

4 仿真分析

4.1 盲分离信号幅度、相位的模糊性

为了验证上述结论的正确性，设线性调频信号(linear frequency modulation, LFM)带宽B为1 MHz，脉宽T为150μs，采样频率fs为2 MHz，幅值A为1，信号初始相位φ0为60°，经过盲源分离后信号幅值和初始相位的变化如图3～6所示。

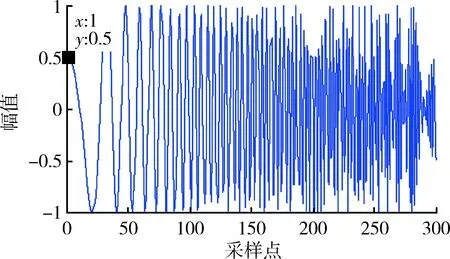
图3 发射信号的时域波形Fig.3 Transmitted waveform

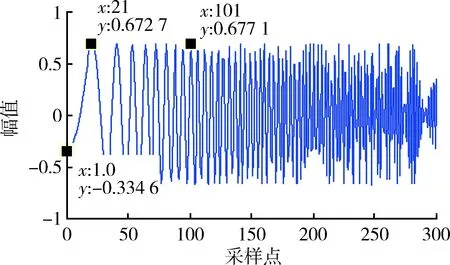
图4 BSS分离后信号的时域波形Fig.4 Waveform after BSS separation

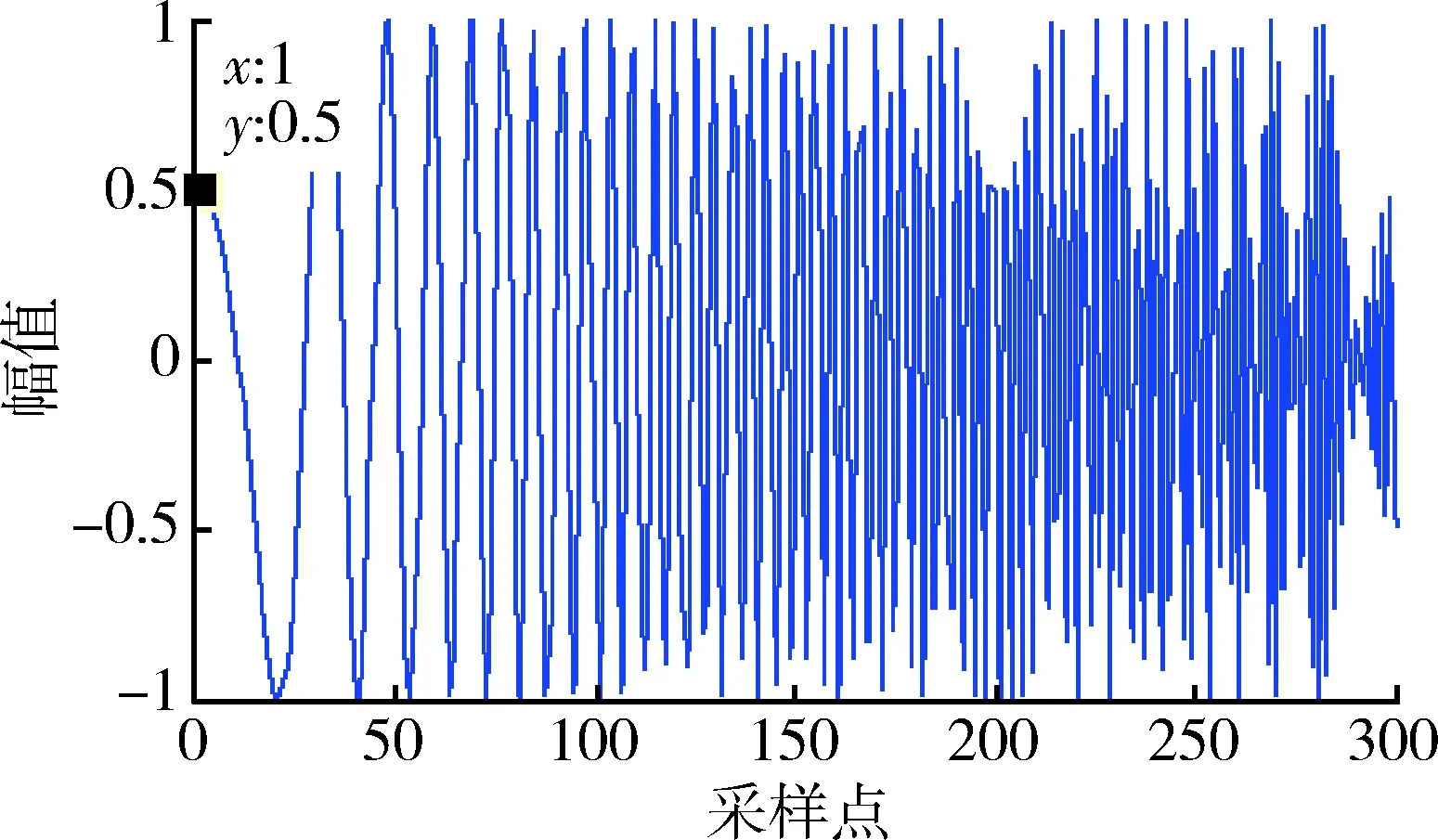
图5 发射信号的时域波形Fig.5 Transmitted waveform

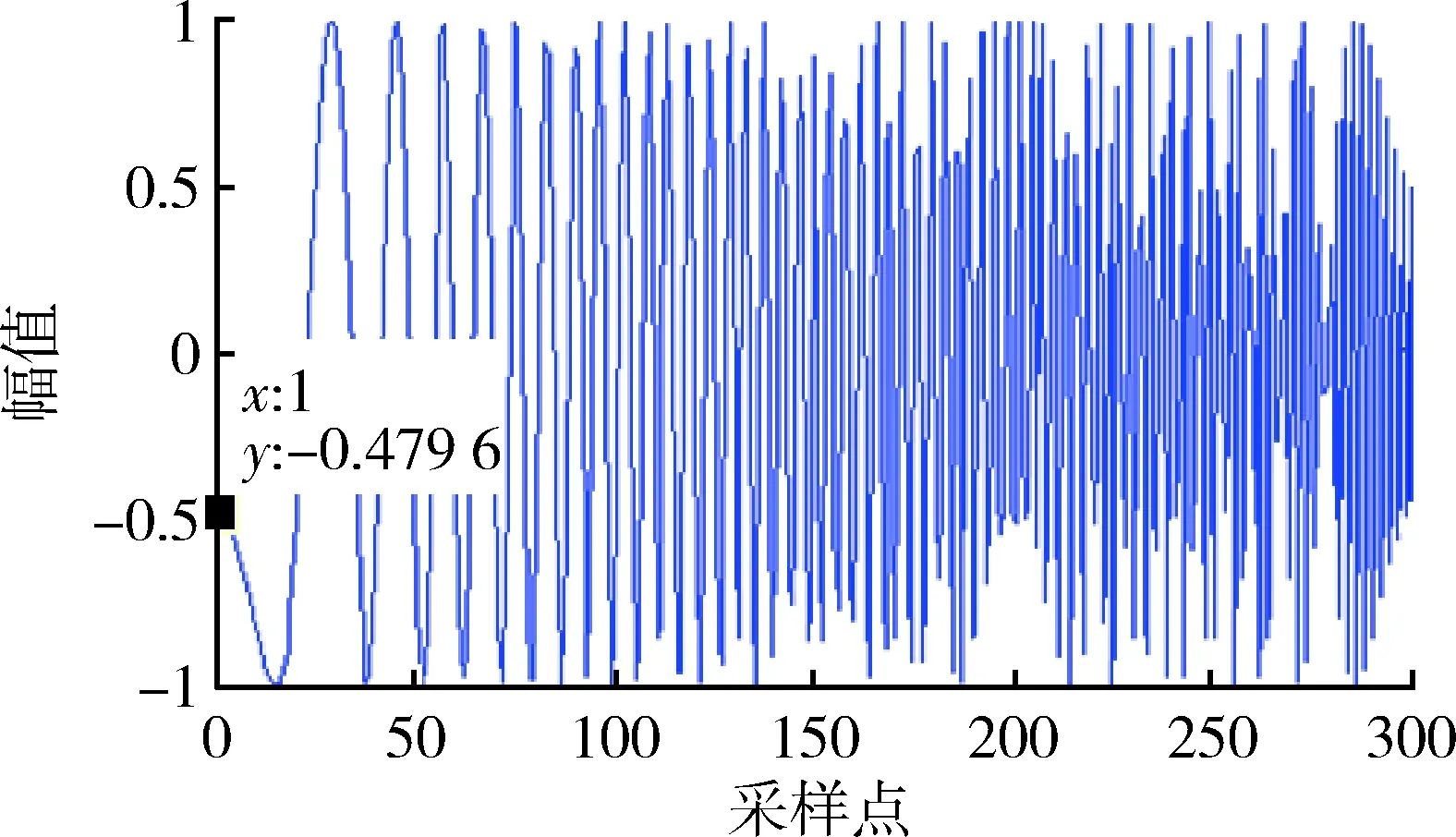
图6 BSS信号归一化的时域波形Fig.6 Waveform of Normalized BSS

图3中信号的幅值为1，图4中盲源分离后信号的幅值近似为0.67。从图3和4中可明显看出，盲源分离后信号的幅度发生了改变，通过归一化使其盲源分离信号幅值保持不变。图5中采样点为1时，幅值为0.5，初始相位φ0为60°；图6的对应采样点为1时，信号的幅值为-0.479 6，初始相位φ0近似为-60°。从图5和图6中可看出，盲源分离信号的初始相位与源信号的初始相位相反。利用100次蒙特卡罗仿真，验证上述结论的正确性，结果如图7，8所示。

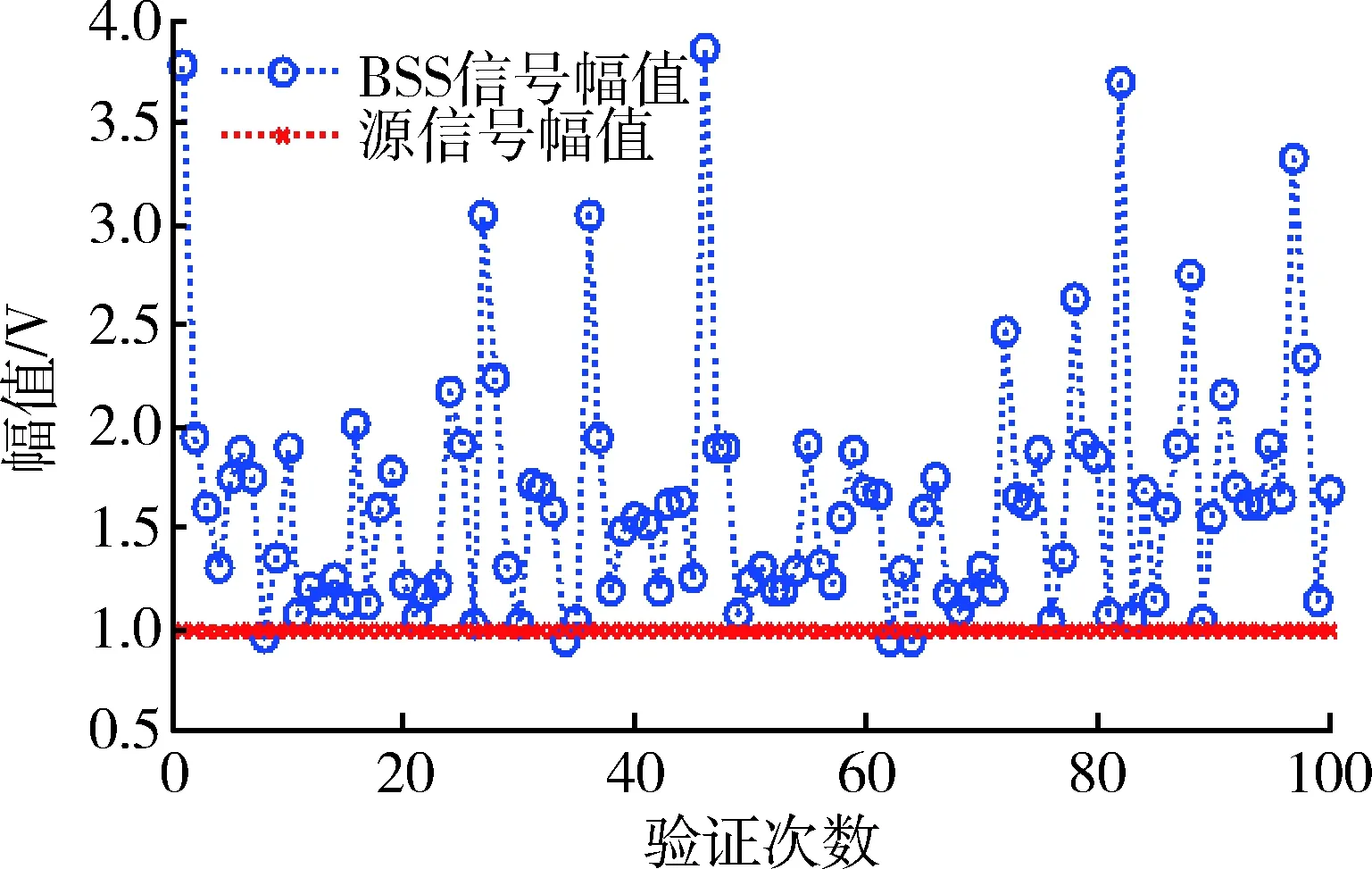
图7 BSS幅值不确定性Fig.7 Uncertainty of BSS amplitude

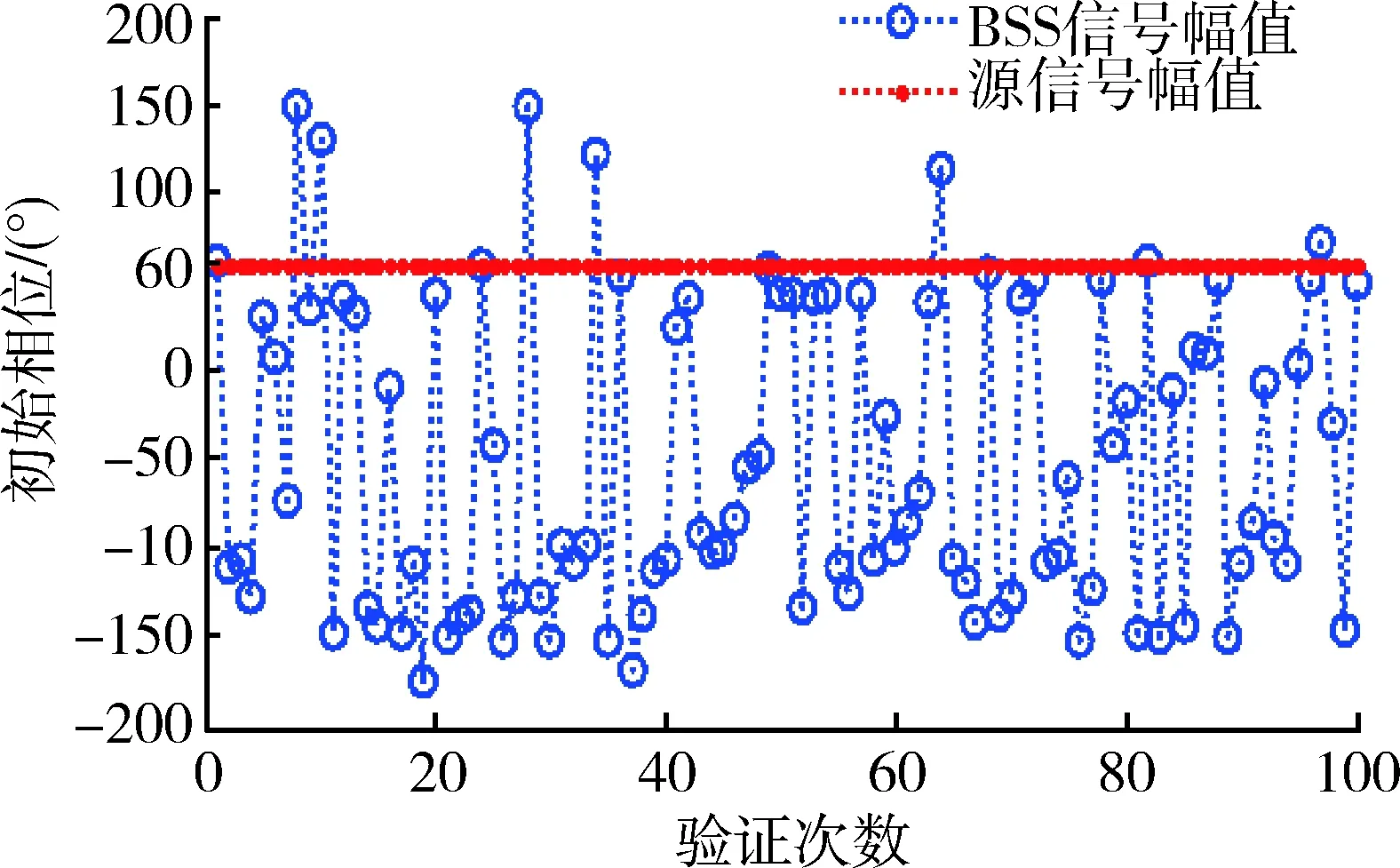
图8 BSS相位不确定性Fig.8 Uncertainty of BSS phase

4.2 信噪比对盲分离信号波形的影响

仿真条件同上，干信比一定条件下，这里的干扰为噪声调频干扰信号。通过分析BSS分离信号与发射信号的相似系数随信噪比的变化，来说明信噪比对盲源分离的影响。结果如图9，10所示。

由图9，10可以看出，当干扰一定时，经过盲源分离的信号与原信号的相似系数随着信噪比增大而增大。

仿真条件同上,当信噪比一定条件下，通过分析BSS分离信号与发射信号的相似系数随干信比的变化，来说明信噪比对盲源分离的影响。结果如图11～13所示。

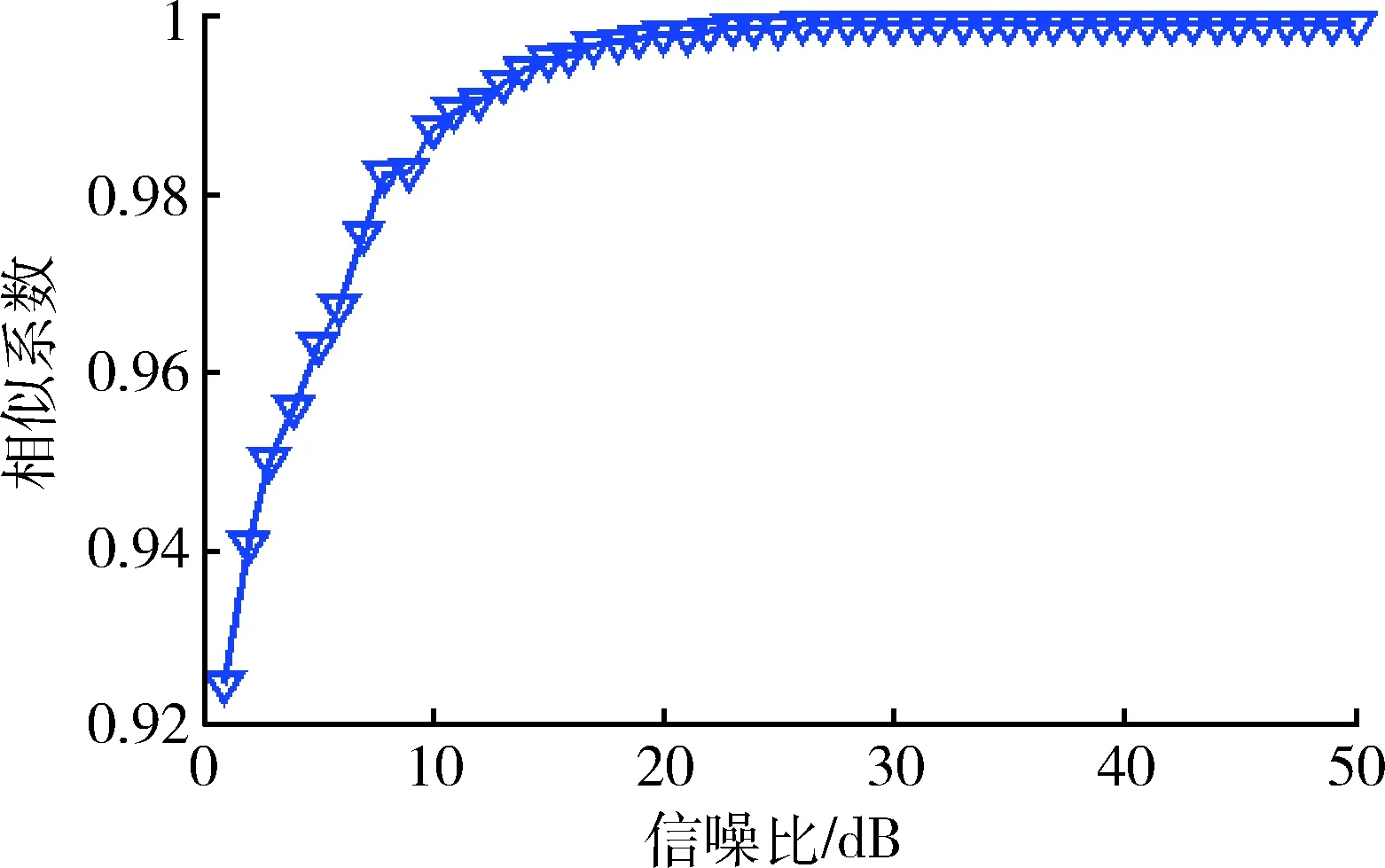
图9 干信比为5 dB相似系数的变化Fig.9 Similarity coefficient curve, ISR=5 dB

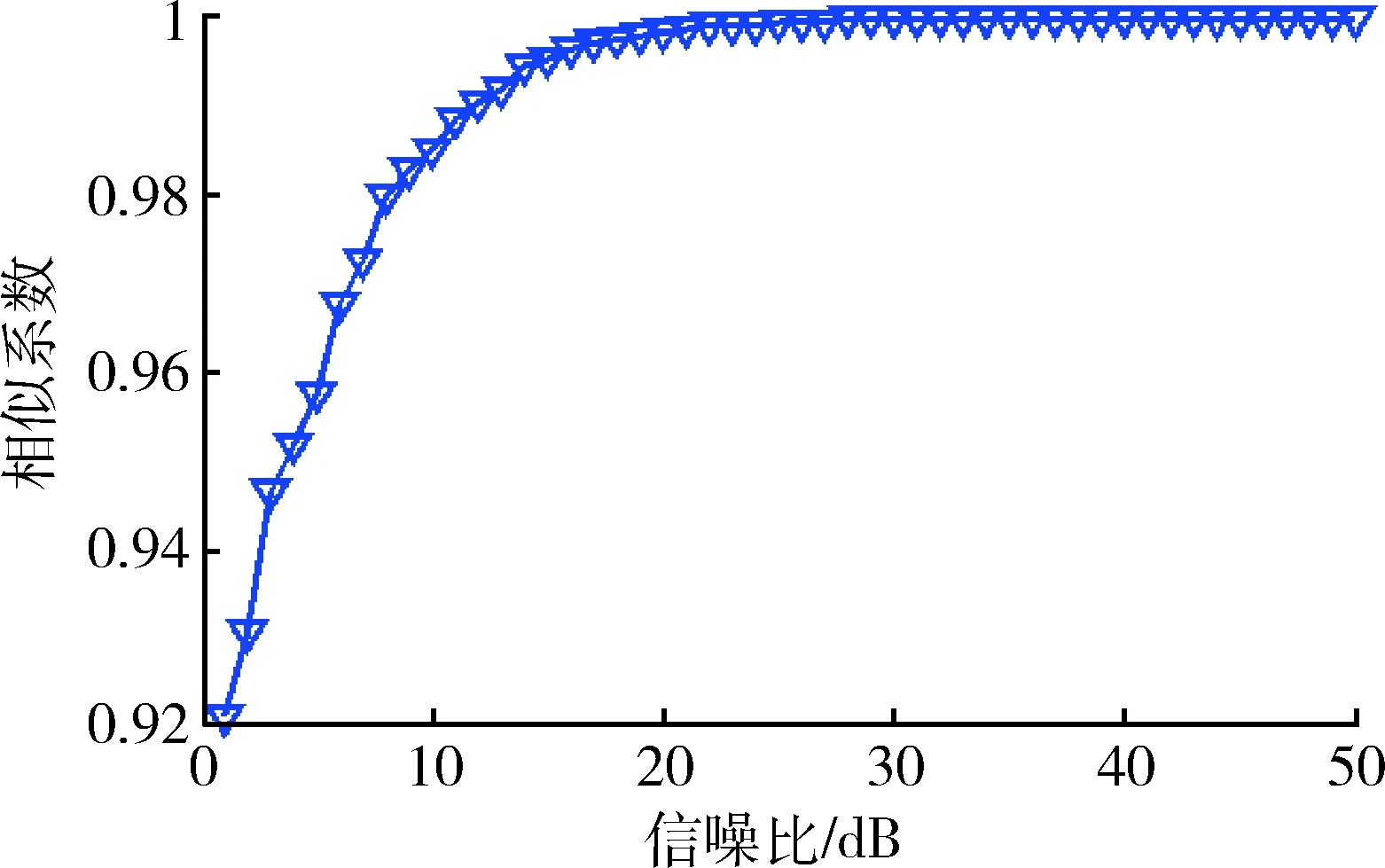
图10 干信比为10 dB相似系数的变化Fig.10 Similarity coefficient curve, ISR=10 dB

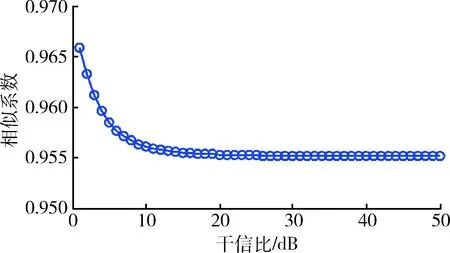
图11 信噪比为5 dB相似系数的变化Fig.11 Similarity coefficient curve, SNR=5 dB

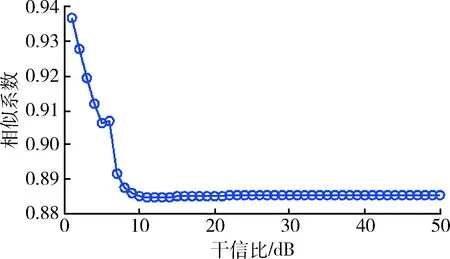
图12 信噪比为-5 dB相似系数的变化Fig.12 Similarity coefficient curve, SNR=-5 dB

图13 信噪比为10 dB相似系数的变化Fig.13 Similarity coefficient curve, SNR=10 dB

从图11～13中可以看出，当SNR较小时，恢复出来的线性调频信号的时域图很难识别；SNR比较大时，恢复的线性调频信号的时域图，即波形的形状都能识别出为线性调频信号，当信噪比达到一定强度时，无论接收到的信号中混有的干扰多强，恢复的信号波形都将不受其影响，即干扰和信号的分离性能最佳。

5 结束语

盲源分离技术在雷达主瓣抗干扰中得到了广泛的应用和研究，但经过理论分析和仿真实验可以得出，经过盲源分离得出的恢复信号存在幅度、相位的模糊性，所以该信号不能用作动目标显示(moving target indication, MTI)，动目标检测(moving target detection, MTD)等一些重要的雷达信号处理。信噪比较大时，恢复的线性调频信号波形的形状都能识别出为线性调频信号;而当信噪比较小时，恢复出来的线性调频信号的波形很难识别；当信噪比达到一定强度时，无论干扰多强，恢复的信号波形将不受其影响。

[ 1] 叶世祥. 盲源分离与雷达信号处理研究[D]. 南京: 东南大学, 2005. YE Shi-xiang.Blind Source Separation and Radar Signal Processing Research[D].Nanjing: Southeast University,2005.

[ 2] 肖文书, 张兴敢, 都思丹. 雷达信号的盲分离[J].南京大学学报:自然科学版, 2006, 42(1): 38-43. XIAO Wen-shu, ZHANG Xing-gan, DU Si-dan. Blind Separation of Radar Signals[J].Journal of Nanjing University: Natural Sciences ed,2006,42(1):38-43.

[ 3] 孙洪, 安黄彬. 一种基于盲源分离的雷达信号分选方法[J]. 现代雷达, 2006, 28(3): 47-50. SUN Hong, AN Huang-bin. A Method to Select Radar Signal Based on Blind Source Separation[J].Modern Radar, 2006,28(3):47-50.

[ 4] 徐梁. 基于忙信号分离和阵列扩展的主动声纳目标回波信号提取[D]. 哈尔滨: 哈尔滨工程大学, 2010. XU Liang.The Study of Target Echo Extraction in Active Sonar Signal Processing Based on Blind Source Separation and Array Extension[D].Harbin: Harbin Engineering University,2010.

[ 5] 徐丽琴. 盲源分离算法研究[D]. 西安: 西安电子科技大学, 2006. XU Li-qin. Research on the Algorithms of Blind Source Separation[D].Xi′an: Xidian University,2006.

[ 6] 王启勇. 目标回波与混响的盲分离技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2012. WANG Qi-yong. Research on the Blind Separation Technique of Target Echo and Reverberation[D].Harbin:Harbin Engineering University,2012.

[ 7] 王翔. 通信信号盲源分离方法研究[D]. 长沙:国防科学技术大学, 2013. WANG Xiang. Research on the Methods of Blind Source Separation for Communication Signals[D].Changsha: National University of Defense Technology,2013.

[ 8] 周郭许. 盲信号分离若干关键问题研究[D]. 广州: 华南理工大学, 2010. ZHOU Guo-xu. Research on Several Key Issues in Blind Source Separation[D].Guangzhou: South China University of Technology,2010.

[ 9] 尹洪伟, 李国林, 卢翠华. 基于盲源分离的单通道LFM引信欺骗干扰抑制[J]. 电讯技术，2014, 54(11): 1475-1481. YIN Hong-wei, LI Guo-lin, LU Cui-hua. Single-Channel LFM Fuze Deception Jamming Suppression Based on BSS[J].Telecommunication Engineering,2014,54(11):1475-1481.

[10] 罗双才, 唐斌. 一种基于盲分离的欺骗干扰抑制算法[J]. 电子与信息学报, 2011, 33(12): 2801-2806. LUO Shuang-cai, TANG Bin. An Algorithm of Deception Jamming Suppression Based on Blind Signal Separation[J].Journal of Electronics & Information Technology,2011,33(12):2801-2806.

[11] 王建明, 伍光新, 周伟光. 盲源分离在雷达抗主瓣干扰中的应用研究[J]. 现代雷达, 2010, 32(10): 46-49. WANG Jian-ming, WU Guang-xin, ZHOU Wei-guang. A Study on Radar Mainlobe Jamming Suppression Based on Blind Source Separation Algorithm[J].Modern Radar,2010,32(10):46-49.

[12] 王文涛, 张剑云, 刘兴华,等. JADE盲源分离算法应用于雷达抗主瓣干扰技术[J]. 火力与指挥控制, 2015, 40(9): 104-108. WANG Wen-tao, ZHANG Jian-yun, LIU Xing-hua,et al. Radar Anti-Mainlobe-Jamming Based on Blind Source Separation Algorithm of JADE[J].Fire Control & Command Control,2015,40(9):104-108.

[13] 周青松, 王文涛, 王珽, 等. 盲分离算法和FRFT联合抗雷达主瓣干扰技术研究[J].信号处理, 2015, 31(8): 1004-1011. ZHOU Qing-song,WANG Wen-tao,WANG Ting,et al. A Study on Radar Mainlobe Jamming Suppression Technique Based on Method of BSS-FRFT Union[J].Journal of Signal Processing,2015,31(8):1004-1011.

[14] 王文涛, 张剑云, 李小波,等. Fast ICA应用于雷达抗主瓣干扰算法研究[J]. 信号处理, 2015, 31(4): 497-503. WANG Wen-tao, ZHANG Jian-yun, LI Xiao-bo,et al.A Study on Radar Mainlobe Jamming Suppression Algorithm Based on Fast ICA[J]. Journal of Signal Processing,2015,31(4) :497-503.

[15] 王春红. 盲信号分离算法研究与应用[D]. 北京: 北京交通大学, 2009. WANG Chun-hong. Researches on Algorithms and Applications of Blind Signal Separation[D].Beijing:Beijing Jiaotong University,2009.

Radar Signal Research Based on JADE Blind Source Separation Algorithm

WANG Yu， LI Xiao-bo， MAO Yun-xiang， HUANG Chao

(Electronic Engineering Institute,Anhui Hefei 230037,China)

Blind source separation technology has received wide attention and application research in the field of radar anti-jamming. So the study of signal based on blind source separation algorithm is crucial. The uncertainty of radar signal amplitude and phase are analyzed based on blind source separation algorithm and through the simulation analysis the influence of signal-to-noise ratio on blind source separation is obtained. The simulation results show that when the signal-to-noise ratio satisfies a certain condition and the blind source separation can separate the signal from the strong interference.

radar anti-jamming; blind source separation; signal to noise ratio；radar signal；amplitude；phase

2015-12-07；

2016-04-25 作者简介：王瑜(1990-)，男，黑龙江巴彦人。硕士生，主要研究方向为雷达信号处理。

10.3969/j.issn.1009-086x.2017.01.025

TN973

A

1009-086X(2017)-01-0147-06

通信地址：510920 广东省广州市从化区城郊镇横江大道333号 E-mail：wangyu117310@163.com