机车轮对经济旋修策略研究*

高 军

(中国铁路济南局集团有限公司 机务处， 济南 250001)

机车在运行的过程中，轮对踏面、轮缘厚度会出现不同程度的磨损，这对机车运行的平稳性和安全性有重要的影响[1]。当轮对踏面和轮缘厚度磨损到一定程度，就必须要通过旋修使得轮对踏面和轮缘厚度恢复到一定程度才能保证机车的正常运行[2]。因此不同的旋修策略对轮饼的使用寿命和经济效益有着重要影响[3]。

目前，国内外在机车轮对旋修策略的研究有Lewis等通过得到的磨耗模型发现若维修工作在运营20万km后进行，其使用寿命可以翻一倍[4]。Branghin在得到基于力学的列车轮对磨耗模型实现有效预测后，依据模型以及预测结果确定了列车的维修时间[5]。Telliskivi在定性得出列车预测方法后，利用相关分析结果对于列车维修给出了相应的建议[6]。Montenegro得到列车轮对运动方程后依据该方程给出了维修指导意见[7]。张宝安等利用列车系统动力学中的轮轨系统磨损接触的接触力、车轮滚动圆直径大小和临界速度做为目标函数，提出了一种动车组车轮型面优化旋修的方法。该方法通过减少车轮外形的旋修量并且可使得车轮旋修时不用旋修到标准型面就可以达到接近标准型面的性能，从而延长车轮的使用寿命，[8]。王凌等提出一种轮对旋修的控制策略，利用蒙特卡罗方法对旋修策略进行仿真，以期望费用为目标函数，对轮对的旋修策略进行优化。通过对广州地铁车辆轮对磨耗实测数据的进行研究分析，研究结果表明当轮对轮缘厚度减小到27～27.5 mm然后旋修到29～30 mm的策略下能够降低旋修的期望费用率，同时延长轮对期望使用寿命。王珍等在建立相关磨耗模型后，以整体最慢磨耗点为旋修标准，建立了单节车厢整体旋修量最少为目标的单目标优化模型[9]。廖贵玲等考虑了轮径值、轮缘厚度值与其相应磨耗速率之间的关系，并建立了相应的磨耗模型，紧接着通过该磨损模型，以列车整体最慢磨耗点为最佳维修值，建立了整车旋修模型[10]。

通过以上研究分析发现，国内外研究者在旋修策略上有一定的研究成果，但主要依赖工程师经验以及工程硬件上的研究，针对机车历史轮对数据进行分析的研究很少。虽然也有一定的研究成果，但是并没有考虑不同轮对磨耗规律的差异，列车不同位置的轮对受力不一样因此磨损上也会存在差异，考虑不同轮对的差异性对旋修策略的研究有重要意义。且没有对整体经济效益、轮对寿命和旋修次数综合考虑旋修策略的给定，只是考虑单方面的因素。综合考虑经济效益、轮对寿命和旋修次数对旋修策略的给出着有利于列车维修的整体提升。因此，本研究首先通过大量历史数据建立轮对磨耗模型挖掘轮对磨损的规律，并通过考虑车轮使用寿命，旋修次数和经济效益建立多目标优化模型，来实现对旋修策略的优化。

1 轮对磨耗模型

轮缘磨耗和踏面磨耗是轮对的主要损耗，而机车在运行过程中会发生轮缘厚度和踏面的直径减少，当轮缘厚度磨损到一定程度就必须要对轮对进行旋修以保证机车运行的安全，轮对旋修是指通过减少踏面直径来恢复轮缘厚度[11]；具体如图1所示。假设轮对旋修后轮缘厚度增加了ΔR，轮径损失为ΔD，则轮对的旋修比例系数为：

根据标准计算k取值为5。

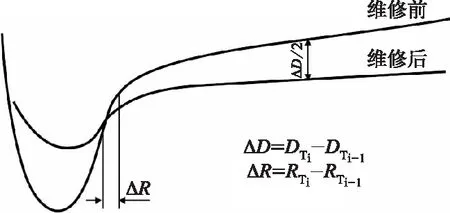
图1 轮对旋修示意图

通过的已有数据的统计分析，发现大部分测量数据间隔在2～7天，因此本研究以5天左右为一个单位时间。轮缘厚度和轮径的磨损速率计算公式如下：

式中VR、VD表示轮缘厚度和轮径的磨损速率，RTi、RTi-1表示Ti、Ti天的轮缘厚度，DTi、DTi-1表示Ti、Ti天的轮径。

为了确定轮径磨损速率、轮缘厚度磨损速率和轮径、轮缘的关系；本研究计算了VR、VD和RT、DT之前的相关系数，并给出轮径磨损速率VD、轮缘厚度磨损速率VD与对应的轮缘厚度的拟合结果。如图2～图3所示。

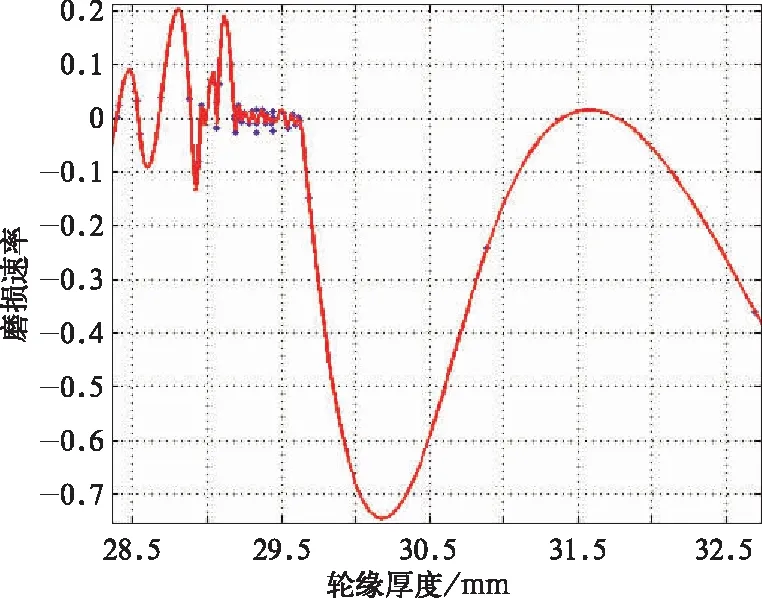
图2 VR拟合曲线

具体相关系数如下表示所示：

表1 相关系数

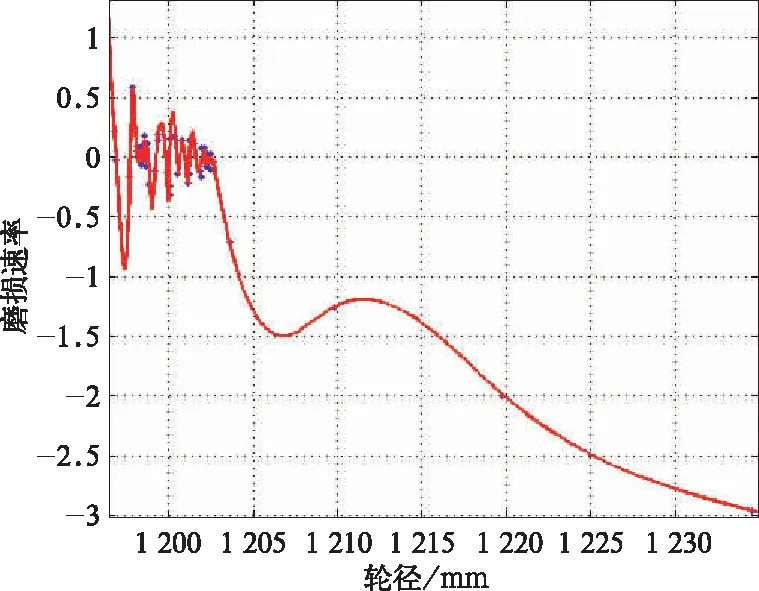
图3 VD拟合曲线

通过计算结果分析，轮缘厚度磨损速率VR以-0.840 2 相关于轮缘厚度R，轮径磨损速率VD以-0.935 2 相关于轮径D；轮径磨损速率VD与轮缘厚度R，轮缘厚度磨损速率VR与轮径D均相互独立。最后得到磨耗函数如下：

VR=1.882×10-2×R3-1.727×R2+

52.64×R-533.3

VD=-2.268×10-4×D2+0.463 6×D-229.7

2 传统旋修策略

本研究是以济南西机务段机车轮径进行研究分析，该机务段机车轮对轮径限值为1 150～1 250 mm，轮缘厚度的限值为23～34 mm。该机务段的传统旋修一般是通过固定旋修策略进行，也就是当机车的轮对轮缘厚度磨损到23 mm后直接旋修到34 mm。旋修周期为2.5年，旋修次数为1。或者是工程人员根据经验进行旋修指导。以上2种方式都存在很大缺陷，第1：没有考虑无法考虑轮对实际的磨损情况；第2：经验旋修存在很大的主观性。因此本研究提出一种机车轮对优化旋修的方法，通过考虑车轮使用寿命、旋修次数和经济效益建立多目标优化模型。这样同时考虑轮对使用寿命、旋修次数和经济效益给出最优的旋修策略。该模型并不考虑剥离、擦伤等对旋修的影响。

3 优化旋修策略

3.1 多目标优化描述

多目标优化问题简单的来理解，就是同时综合考虑多个因素的影响，从而给出问题的最优解决方案。也就是同时包含两个或者两个以上的目标函数，并且在可行域中确定由决策变量组成的向量，使得一组互相冲突的目标函数的值同时达到极小[12]。表现形式如下所示：

max/minf1(x)

max/minf2(x)

⋮

max/minfk(x)

s.t.x∈S

式中k是优化目标个数，S是优化问题的可行域。max/minfk(x)为目标函数。

NSGA-II算法是现在应用较为广泛的多目标优化算法之一。NSGA-II提出了快速非支配排序，该方法保留了可行解中可以支配的当前解的个体数量和被当前解支配的所有个体的集合，相比于NSGA算法，NSGA-II算法时间复杂度由O(NM3)提升至O(NM2)。并且NSGA-II算法通过精英个体的选择策略，大大的增大了下一代种群的采样空间。此外，NSGA-II通过拥挤距离来衡量同层Pareto前沿的个体多样性，并以此为准则在截断层选取相应的个体，使解空间能够均匀扩展，从而保证了种群的多样性[13]。

NSGA-II算法的基本思想为：首先，随机产生初始种群，其规模为N；在进行非支配排序后，通过遗传算法的交叉、变异和选择这3个操作得到第1代子代种群；然后从第2代种群开始，将父代种群与子代种群合并，并进行快速非支配排序，同时计算每个非支配层中的个体的拥挤度，通过非支配关系以及个体拥挤度来选择较优的个体来组成新的父代种群；最后，通过遗传算法产生新的子代种群；依此类推，直到满足程序结束的条件[14]。相应的程序流程图如图4所示。

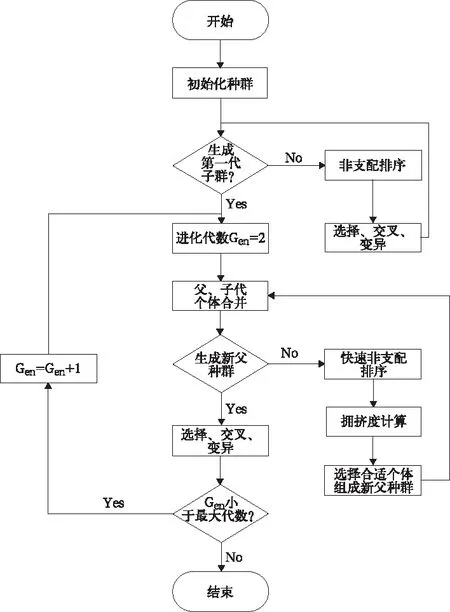
图4 程序流程图

3.2 多优化模型的建立

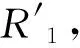
maxYear=

式中N为轮对旋修次数。

轮径在机车运行和旋修中均会磨耗，为了减少轮径在旋修工作中的损失，降低轮对维修费用，旋修次数应尽可能的少，因此第2个优化模型的目标函数为：

minF=min{N}

文献[15]中指出一个精加工的轮饼价格为5 373元，一个轮对价格为10 745元，而该文中的轮饼轮径范围为770～840 mm，因此每个轮对旋修损耗1 mm 就相当于损耗153.5元。因此，考虑可以通过轮径的损耗来衡量经济效益，由于现在一直只有旋修费用和换轮费用，通过以式(1)计算每损耗1 mm轮径的费用：

(1)

式(1)中，LM表示每损耗1 mm轮径费用；LS表示轮径上限，取值为1 250；LX表示轮径下限，取值为1 150；CT表示旋修一次的费用，取值为300元；CR表示换轮费用，取值为18 300元，其中包括人工费用、调车费用和轮饼费用；NT表示旋修次数。标准旋修策略的旋修次数为1，通过标准旋修策略计算可得，每损耗1 mm轮径消耗费用为186元/mm。因此第3个优化模型的目标函数为：

minMoney=

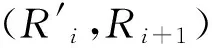
maxYear

minFre

minMoney

3.3 改进的NSGA-II算法

NSGA-II算法通过对NSGA算法增加精英保留策略、利用计算拥挤距离值作为密度估计策略和快速非支配排序策略，提高了NSGA算法参数选取难的效率并且减少了算法运行时间[16]。但通过对NSGA-II研究发现，该算法还可以在如何提高种群收敛性、增强全局搜索能力和提高算法运算效率等方面进行研究。

笔者主要通过从提高算法的全局搜索能力对来对算法进行改进研究。NSGA-II算法通过交叉算子(SBX，Simulated Binary Crossover)来进行交叉操作，SBX可以把父代中的优秀个体基因遗传到下一代中去，使得子代具有父代的优秀基因，可以确保遗传算法收敛于全局最优解[17]。具体定义如式(2)：

(2)

为了提高交叉算子的全局搜索能力，使用算数交叉算子来替代SBX交叉算子，该算子引入了个体当前的Parteo非支配排序级别的信息，具体定义如下：

式中Afront、Bfront分别表示个体A、B的非支配排序赋值。每个个体在种群中Pareto非支配排序级别都与该交叉算子α相关。因此，这种方式在算法迭代的初期，因为种群个体的多样性，交叉算子变化比较大，因此Pareto非支配排序值较小的个体在后代中占比较大的比例。但随着迭代次数的增多，种群中个体都会趋于一个稳定的Pareto非支配解，这里该交叉算子α会趋于0.5。

4 试验与分析

4.1 试验数据

本研究的试验数据来自于济南西机务段HXD3-8118号机车，该试验数据是从2017年4月1日到2017年11月30日期间的实测数据，时间间隔为243天，总共130×12条；由于原始数据采集时间间隔不一致，并且存在一定的误差。因此需要对数据进行预处理，首先对数据进行去噪处理，去除不合理数据的影响；如图5～图6所示。

然后，对去噪后的轮缘厚度数据进行插值操作，使数据点之间的时间间隔相同，这里设置的时间间隔为5天。如图7所示。

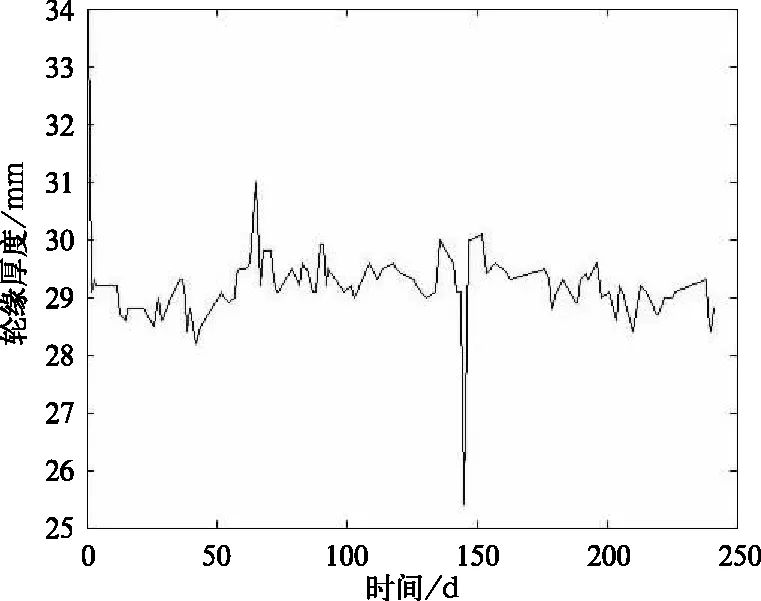
图5 原始轮缘厚度数据

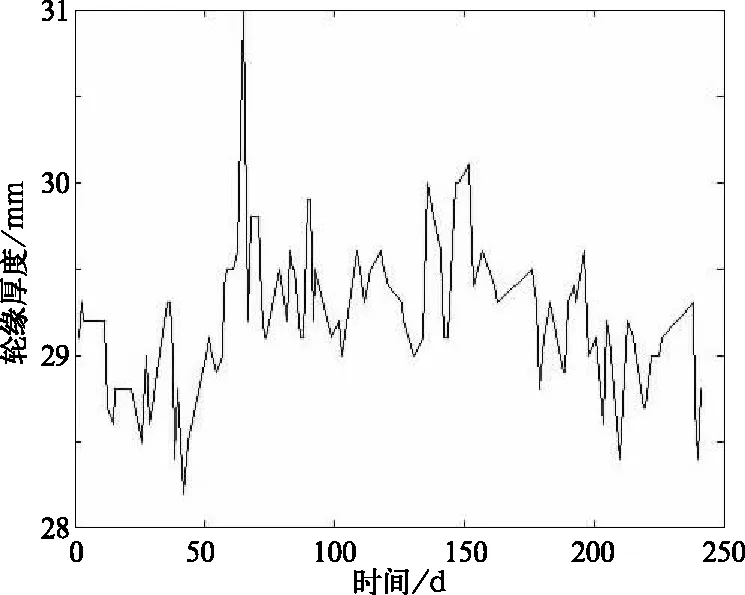
图6 去噪后轮缘厚度数据

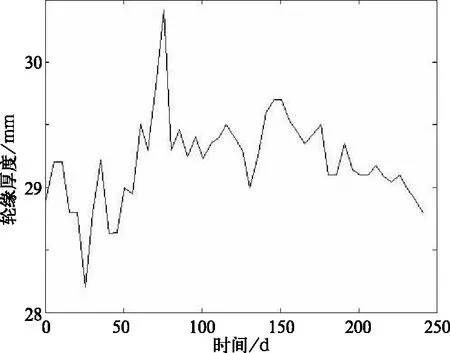
图7 插值后轮缘厚度数据

最后，对插值后的数据进行拟合处理，使得插值后的轮缘厚度数据变平滑，从而符合轮缘厚度磨耗模型；拟合后的轮缘厚度数据样本点之间的时间间隔也为5天。具体如图8所示。

4.2 试验结果与分析

本研究通过与固定旋修模型和传统的NSGA-II进行试验对比，通过比较寿命，旋修次数和经济效益判断优化模型的优劣。研究对象济南西机务段HXD3-8118号机车轮缘厚度范围为23～34 mm，轮径范围为1 150～1 250 mm。

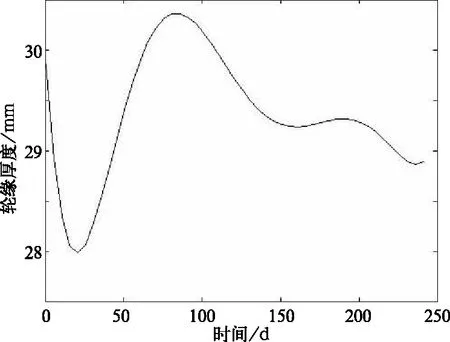
图8 拟合处理后轮缘厚度数据

(1)固定旋修仿真

固定旋修次数为1次，寿命为5年。固定旋修是指当机车轮对轮缘厚度磨耗至23 mm时，不考虑其他影响因素，直接将其恢复至34 mm。因此，首先对固定旋修[23,34]进行仿真，图9所示即为仿真结果。

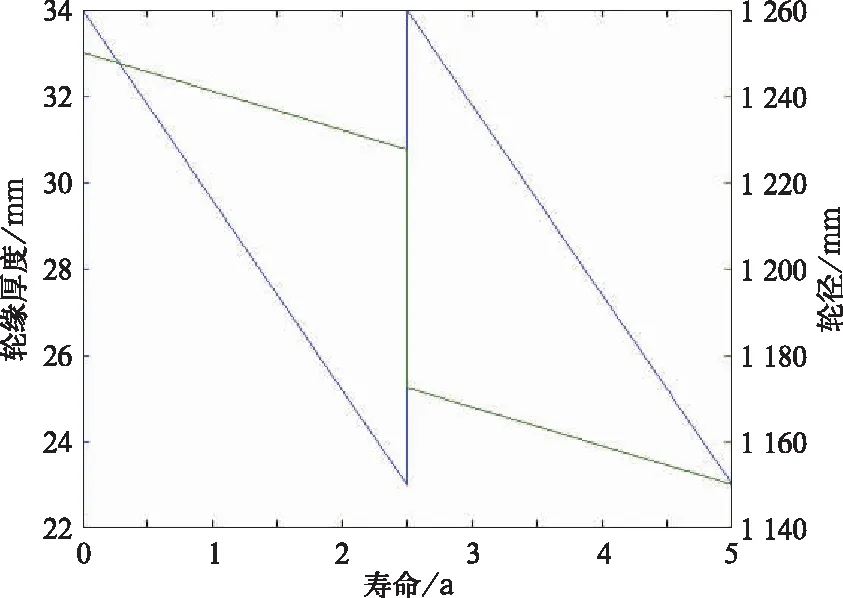
图9 固定旋修仿真结果

通过第3.2节旋修经济效益计算公式可得，标准旋修策略每损耗1 mm轮径消耗费用为186元/mm。

(2)磨损速率模型仿真

已有研究表明，在不同的轮缘厚度下，轮缘厚度的磨损速率是不一样的，因此有研究者通过轮缘厚度的磨损速率来计算旋修模型，本研究通过计算不同轮缘厚度下轮缘的磨损速率，取磨损速率较为缓慢的区间为旋修区间，这里取值范围为70%。仿真结果如图10所示。

通过上述仿真结果可以看到，磨损速率模型计算的旋修策略为[28.2，30.3]，旋修8次，在该策略下轮对使用寿命为5.96年，相比固定旋修轮对寿命5年提升了19.2%。经济损耗相比固定旋修节省了2 939元。

(3)NSGA-II模型仿真

在每一组旋修策略中，旋修次数不定且被期望最小、轮对使用寿命和经济效益不定被期望最大。利用第2节的轮对磨耗模型和第3.2节建立的多目标仿真模型对旋修策略进行优化，结果如图11所示。

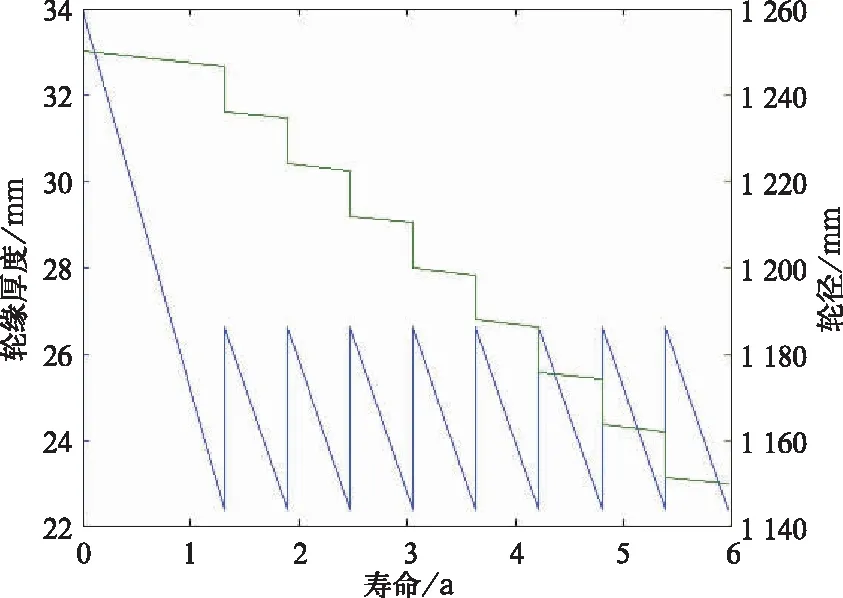
图10 磨损速率仿真结果

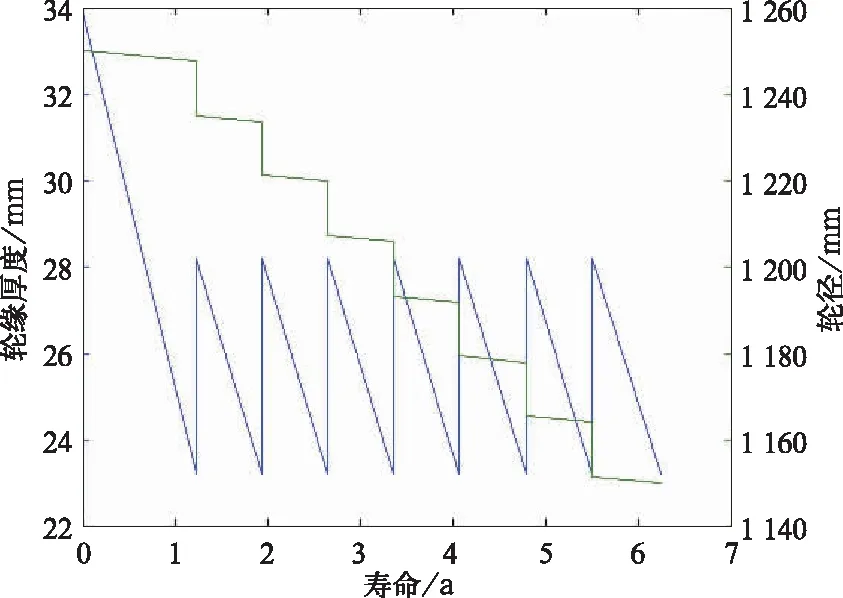
图11 NSGA-II模型仿真结果

通过上述仿真结果可以看到，NSGA-II模型计算的旋修策略为[28.6，29.7]，旋修7次，在该策略下轮对使用寿命为6.23年，相比固定旋修轮对寿命5年提升了26.4%。经济损耗相比固定旋修节省了3 627元。相比磨损速率模型得到的旋修策略对寿命5.96年提升了4.53%。经济损耗相比磨损速率模型得到的旋修策略节省了688元。

(4)改进的NSGA-II模型仿真

通过第3.3节改进的NSGA-II算法对多目标仿真模型对旋修策略进行优化，

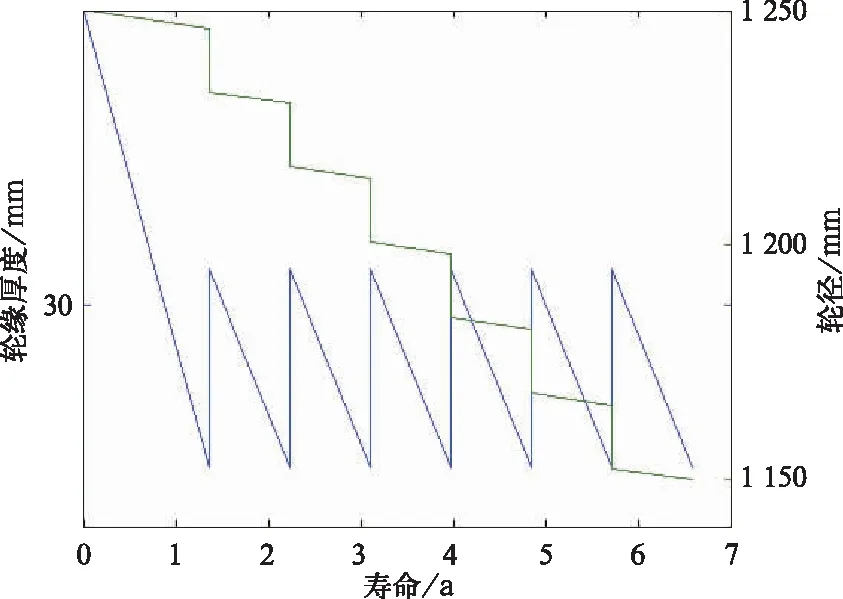
图12 改进的NSGA-II模型仿真结果

通过上述仿真结果可以看到，改进的NSGA-II模型计算的旋修策略为[28，29.5]，旋修6次，在该策略下轮对使用寿命为6.57年，相比固定旋修轮对寿命5年提升了31.4%。经济损耗相比固定旋修节省了3 914元。相比磨损速率模型得到的旋修策略对寿命5.96年提升了10.2%。经济损耗相比磨损速率模型得到的旋修策略节省了975元。相比NSGA-II模型得到的旋修策略对寿命6.23，年提升了5.46%。经济损耗相比NSGA-II模型得到的旋修策略节省了287元。

通过上述试验分析改进的NSGA-II模型的得到的旋修策略相比固定旋修、磨耗速率模型旋修策略和NSGA-II模型旋修策略，在使用寿命和经济损耗上均有提高。

5 结 论

在车轮的磨耗模型的基础上，根据车轮现实情况建立多目标优化模型；并在优化模型和旋修策略的实际需求下，提出了改进的NSGA-II模型。最后，利用济南西机务段的实测数据进行仿真试验，仿真结果表明：改进的NSGA-II模型得到的旋修策略相比固定旋修、磨耗速率模型旋修策略和NSGA-II模型旋修策略，在使用寿命和经济损耗上均有提高；这说明了改进NSGA-II模型在车轮旋修策略的制定上的有效性和适用性。

[1] 陆缙华. 广州地铁一号线车辆的磨耗情况分析[J]. 电力机车与城轨车辆, 2001, 24(3):16-17.

[2] 员 华, 肖胜强, 汪 洋. 基于磨耗量统计的轮对等级旋修可行性分析[J]. 城市轨道交通研究, 2006, 9(1):43-45.

[3] 曾全君. 地铁车辆车轮寿命分析[J]. 电力机车与城轨车辆, 2005, 28(2):47-49.

[4] Lewis R, Olofsson U. Mapping rail wear transitions[J].Wear,2004，(257):721-729.

[5] Braghin F, Lewis R, Dwyer-Joyce R S, et al. A mathematical model to predict railway wheel profile evolution due to wear[J]. Wear, 2006, 261(11-12):1253-1264.

[6] Telliskivi T. Wheel-Rail Interaction Analysis[J]. Mask- inkonstruktion, 2003.

[7] Montenegro P A, Neves S G M, Calçada R, et al. Whe- el-rail contact formulation for analyzing the lateral train-structure dynamic interaction[J]. Computers & Structures, 2015, 152(4):200-214.

[8] 张宝安, 陆正刚, 唐 辰. 高速动车组车轮型面多目标优化旋修[J]. 同济大学学报(自然科学版), 2013, 41(3):437-442.

[9] 王 凌, 员 华, 那文波,等. 基于磨耗数据驱动模型的轮对旋修策略优化和剩余寿命预报[J]. 系统工程理论与实践, 2011, 31(6):1143-1152.

[10] 廖贵玲. 城轨列车轮对安全状态分析预测与旋修策略优化方法研究[D]. 北京：北京交通大学, 2014.

[11] J. De Arizon, O. Verlinden, P. Dehombreux. Prediction of wheel wear in urban railway transport: comparison of existing models[J]. Vehicle System Dynamics, 2007, 45(9):849-866.

[12] 成 棣, 王成国, 刘金朝,等. HXD2型电力机车车轮型面的多目标优化[J]. 中国铁道科学, 2013(1):75-81.

[13] Deb K, Agrawal S, Pratap A, et al. A Fast Elitist Non-dominated Sorting Genetic Algorithm for Multi-objective Optimisation: NSGA-II[C]// International Conference on Parallel Problem Solving From Nature. Springer-Verlag, 2000:849-858.

[14] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA—Ⅱ[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197.

[15] 孙小康. 地铁轮对踏面旋修经济性分析[J]. 城市轨道交通研究, 2016, 19(5):91-92.

[16] 蒋 勇, 李 宏, 焦永昌. 改进 NSGA—Ⅱ 终止判断准则[J]. 计算机仿真, 2009 (2): 196-200.

[17] Li H, Zhang Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA—Ⅱ[J]. IEEE transactions on evolutionary computation, 2009, 13(2): 284-302.