基于局域声子理论的铝合金型材低频降噪研究

肖友刚， 邓 微， 申肖雪， 卢 浩

(中南大学 交通运输工程学院， 长沙 410075)

近几年来,我国的高速铁路发展迅猛, 因为其安全性强、速度快、舒适度好，所以逐渐成为人们生活出行的主要方式。随着我国高速列车运行速度提高，振动和噪声问题日益突显，车辆车体的零部件材料及减振结构的设计显得尤为重要[1]。2000年Liu等人在《Science》上首次提出了声子晶体产生带隙的局域共振机理[2]。局域共振机理的提出为结构减振降噪的理论和技术突破提供了新的契机。低频噪声一般通过固体传声且不易衰减。低频噪声对人体的危害很大，如果长期受到低频噪声袭扰，容易造成神经衰弱、失眠、头痛等各种神经官能症[3]。

目前国内外对声子晶体和声学超材料的研究大部分都集中在理论阶段，在微观上通过分析声波在不同介质中的传递损失。文中将局域声子晶体机理的思想结合类动力吸振器的结构模型来分析局域声子板。类动力吸振器结构模型能够有效地的消耗固有频率附近的低频振动能量且其质量比越大，其吸振效果越明显，通过其质量弹簧构成的多自由度的共振系统的低频振动吸收过来并加以增幅，最后消耗在阻尼元件中，达到抑制高速列车地板低频振动的良好效果。

对于整个系统的研究，为了更贴近实际的声—固结构耦合的多物理场分析，故采用多物理场商业仿真软件COMSOL-Multiphysis进行仿真试验，首先验证仿真软件对隔声量计算的准确度，然后对参数及物理场边界条件的设置以及边界的约束和入射声压进行合理的设置。

通过仿真得出低频频域范围内的隔声量，然后改变结构位置，得出最优的结论，为实用工程生产设计提供可靠的科学依据。

1 铝型材外地板三角筋板研究

高速列车地板主要包括外地板、间夹层、内地板。将局域声子板敷设于外地板上方，选择目前在高速列车地板中使用最广的三角筋板结构进行分析如图1示，根据文献(4)的研究选用最优化的结构设计并利用商业软件COMSOL-Multiphysis参数化设计建立高速列车铝型材地板三角筋板结构的三维模型，模型的长度为2 240 mm。宽度为1 800 mm,厚度为40 mm,上筋板厚度为3 mm,下筋板为2.5 mm，加强筋为1.8 mm，根据筋板的结构特征，将结构形式设为壳单元薄板形式(如图1)。并对铝型材筋板结构进行模态分析，根据实际在安装过程中对筋板的四周进行边界约束的情况，设置边界固定约束，对地板结构的前六阶的固定频率进行仿真计算得到数据如表1。

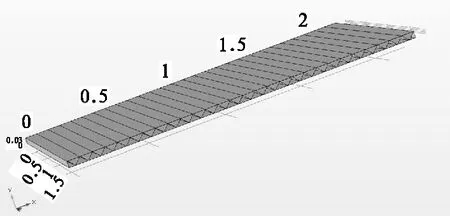
图1 铝型材三角筋板模型

表1 结构振动模态分析

铝型材三角筋板上局域板结构优化设计:根据参考目前声学超材料[5-6]在声学领域的研究成果及计算局域共振板声透射特性—等效介质法[7]，将局域声子板等效为动态质量密度的各向同性均质板结构可得到局域声子板中吸振器与基体板的质量比μ。根据Den Hartog参数调整公式[8]阻尼动力吸振器设计原理确定最佳调谐频率比λ，吸振器的等效弹簧刚度k，橡胶的黏性阻尼系数c。如下式

(1)

(2)

(3)

c=2mω0

(4)

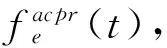
(5)

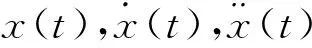
2 铝型材筋板结构隔声量计算和优化

2.1 结构模型声学仿真准确性验证

借助多物理场商业仿真软件COMSOL-Multiphysis对模型进行仿真计算，首先需要验证仿真的准确性，将薄板的仿真结果和马大猷所著的《噪声与振动控制工程手册》[10]中所进行的试验得到的数据进行对比，选取的对象为长×宽×高分别为1 000 mm×1 000 mm×1 mm的铝板进行分析，对照结果如表2。

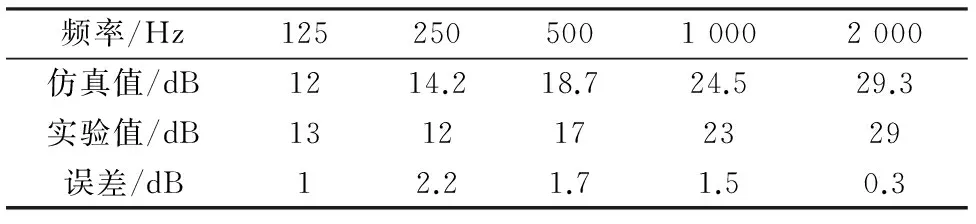
表2 仿真值和实验值的对照结果

仿真的误差产生的原因大致为实际测试和仿真的边界条件设置不一致，其实为有限元网格划分的精度影响，材料的参数以及板内部阻尼损耗因子的设置造成的，不过从仿真值和试验值观察属于工程设计合理的误差范围之内。

2.2 铝型材模型结构隔声量计算及优化

对铝型材地板三角筋板进行声透射隔声计算 首先利用商业软件COMSOL-Multiphysis参数化设计建立几何模型、然后再设置材料参数和载荷、定义边界约束条件、剖分网格等。其中在声场域中设置的流体材料为空气，参数从材料库内自定义设置材料参量见表3，由于在空气中中低频声波的传播主要是平面波的传播，所以采用1 Pa的声压值设置平面波入射场声压,筋板四周设置固定约束，有限元的网格一个声波波长内含有6个单元进行划分，对声学和结构的交界面，设置声—固结构边界进行模拟声固耦合的物理关系，模型中对声场域的入射面以及透射面进行平面波辐射，然后对入射面和透射面声能量进行积分，隔声计算模型如图2通过式(7)，计算声能量损失TL(dB)

TL=10ln(ωin/ωout)

(6)

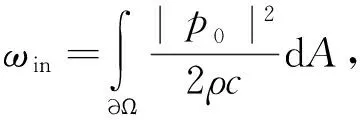
(7)

式(6)～式(7)中ωin代表入射声能量，ωout代表透射声能量，p0代表入射声压值，p代表透射声压值，ρ，c分别代表空气的密度及声速。

分析的频域范围为低频的隔声，所以计算的频域从100 Hz到500 Hz,隔声量如图3所示。

从铝型材的裸筋板隔声量分析知，从100 Hz到120 Hz之间为刚度控制区，在这区域内刚度越大，隔声量越高，在这范围内随着频率的增大筋板开始振动到达一阶临界频率共振频率时隔声量降到最低点，几乎为全部透射出去。然后进入阻尼控制区，当外部激励频率和筋板的固有频率接近或者一致时，筋板发生共振现象，在这一区域随着阻尼的增大，隔声量有较明显的增大。

表3 材料参量

图2 铝型材隔声计算模型

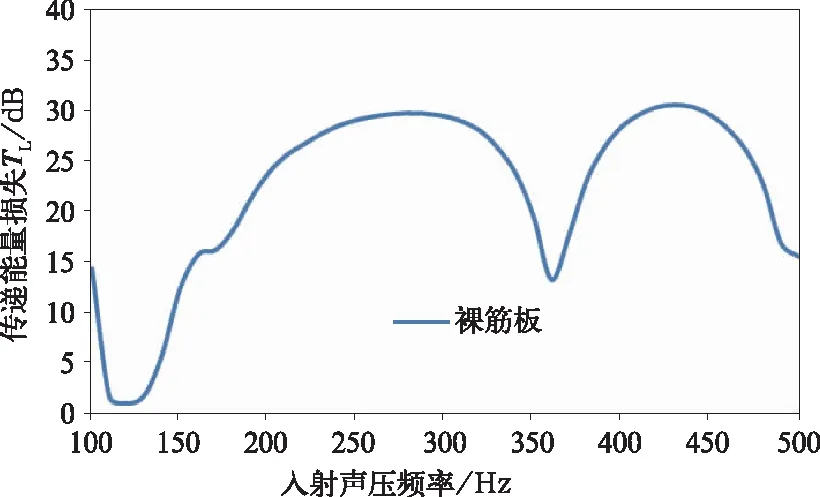
图3 铝型材裸筋板隔声量

2.3 阻尼层对铝型材三角筋板的隔声影响

根据文中对阻尼吸振器设计原理的分析结合高速列车的轻量化的设计理念，参考文献[11]可以得到当质量比u设置得越大对板的抑制效果越好同时对声能的损耗也越好即隔声量越高，但是和轻量化设计理念不符，所以将质量比u初始为0.1，根据公式计算在上筋板面上敷设5 mm的橡胶层,剩余的质量设置其他的质量块，如图4所示，其中阻尼层橡胶刚度等效为吸振器的等效弹簧刚度，橡胶本身含有阻尼，所以适用阻尼吸振器设计原理来设计。

当添加5 mm的橡胶层后在500 Hz范围内平均有2 dB的衰减，对低频隔声的效果比较明显。铝型材隔声量如图5所示。

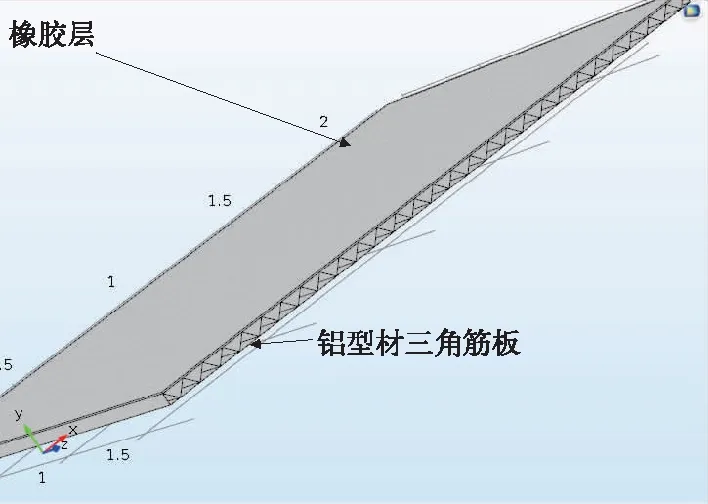
图4 铝型材加阻尼层模型

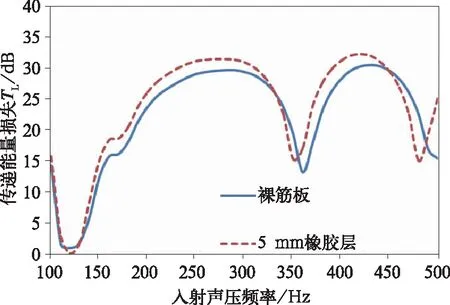
图5 铝型材加阻尼层隔声量

2.4 阻尼层上添加整块铅片

根据阻尼动力吸振器的设计原理，在橡胶层上添加0.2 mm的全部覆盖橡胶的铅片，在Y方向构成质量(筋板)—弹簧(含阻尼)—质量(整块铅片)结构，当入射声波频率等于局域声子板的固有频率时那么局域共振模态被激发，在Y方向产生一个F,而添加整块铅片后对橡胶层产生一个反力，虽然振动受到了抑制，但是弯曲波的横波在XZ平面能够继续传播，所以从图中结构隔声量我们可以得到在二阶模态附近有一个较大的隔声量，但是又出现一个相似的隔声低谷。同时在分析频域范围内由于铅片的质量原因平均提高了2 dB左右。由分析可以知道，通过添加质量块可以得到一个改进频率，也就是模态固有频率的改变。

根据模态分析的结果将动力吸振器上的质量块附加于各阶模态的波峰位置，抑制各阶模态下三角筋板的振动，减小筋板的振幅，从而提高隔声量。从铝型材的前六阶的固有频率振型图能直观的得到相应的振动波峰。从图3上铝型材裸筋板的隔声量曲线，在122，350，470 Hz附近产生隔声低谷。由文献[12]知，在等质量密度的情况下增加子吸振器的个数，可以明显拓宽局域共振板的改进频率，同时恶化频率移向更高频段，这对低频的隔声处理是非常有益的。根据波峰位置、隔声低谷的情况，设置12块薄铝片(尺寸0.2 m×0.3 m×0.000 05 m，结构单元可以简化为在XZ平面形成质量(铅片)—弹簧(橡胶)—质量(铅片)，这样质量块铅片形成12个子吸振器， 单元结构可以简化为图6所示。这样在XZ平面形成铅薄片和橡胶成二维二组元的局域声子板结构，如图7所示。根据振型图可以观察到在模态固有频率处，能量集中在XZ平面的铅片之间的橡胶处，当弹性波的频率接近共振单元的固有频率时，XZ平面的铅片就会产生一个反力F′,这样弹性波的能量在通过局域共振能量消散在橡胶层中，从结构隔声曲线图8中，我们可以对比同质量的整块铅片和分布式铅片在低频端隔声有很大的提高，特别在122 Hz附近处的隔声达到了30 dB,在360 Hz附近处也有10 dB的提高。同时在250 Hz附近处会有一个改进频率，但是相对122 Hz频率的隔声量也提高了5 dB。通过仿真得到结论，打破了隔声的质量定律，在传递过程中通过质量—弹簧—质量的局域共振结构消耗了声能即提高了隔声量，同时也满足能量守恒定律。

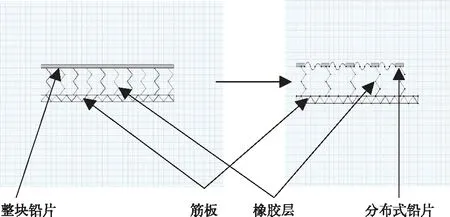
图6 弹簧—质量、质量—弹簧—质量模型

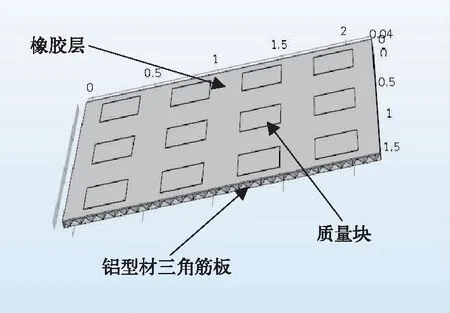
图7 铝型材敷设局域声子板的模型

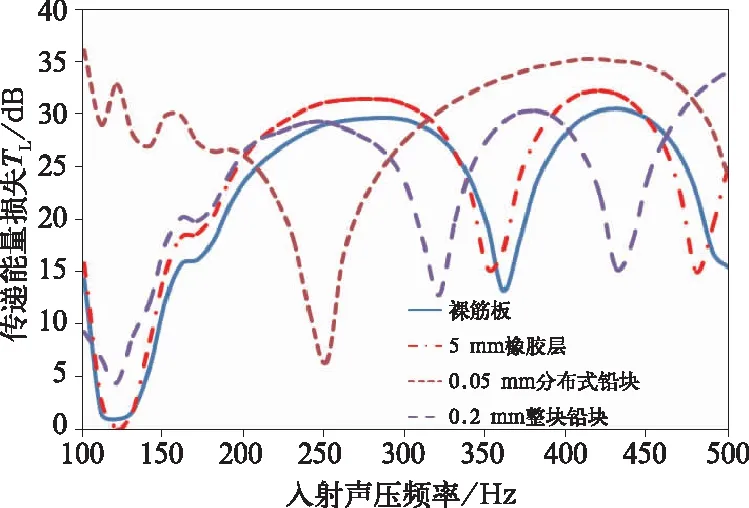
图8 铝型材各种结构隔声量比较

3 铝型材三角筋板仿真与试验对比分析

选取铝型材筋板模型尺寸长×宽=1 500×1 200 mm,上板、加强筋、下板厚度分别为2.5,1.8,3 mm的铝合金型材三角筋板在频率范围100 Hz到500 Hz的1/3倍频段(100，125，160，200，250，315，400，500 Hz)进行现场声强法隔声试验，如图9。

然后用comsol仿真软件将模型数据进行仿真，可以得到隔声量的试验值和仿真值结果如图10所示。

根据试验对比分析，软件仿真在边界条件的设置上过于理想化，导致低阶的模态频率产生较大的差异，同时在低频段试验漏声严重，导致在250 Hz处误差较大，但其他倍频处有很好的拟合，证明仿真和试验的准确性。

最后在铝型材筋板上添加局域声子板后隔声的仿真值与未添加局域声子板的试验值以及仿真值的对比，如图11所示。

图9 声强法隔声试验

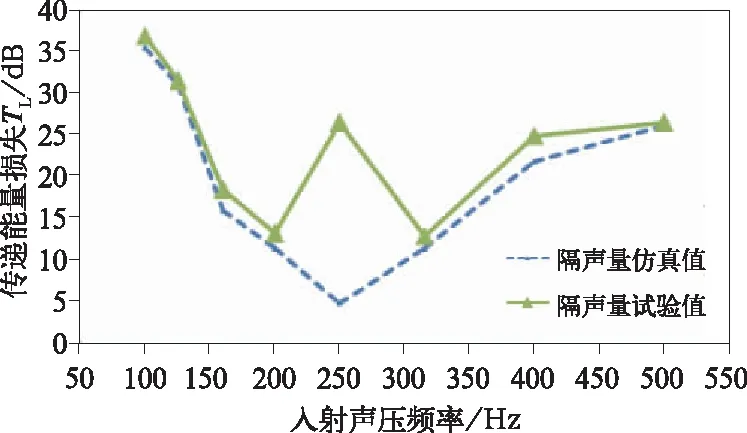
图10 铝合金型材试验对比分析

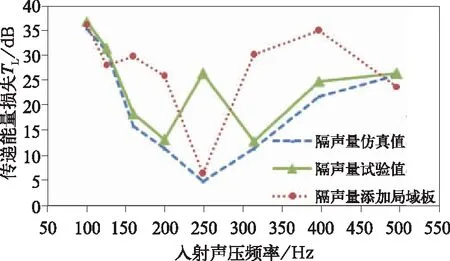
图11 铝合金型材添加局域声子板仿真对比分析

从图11我们所知，在铝型材板上添加局域声子板后在频率(100～500 Hz)范围内1/3倍频段隔声效果有显著的提高。

4 结 论

(1) 通过分析多系统结构振动的理论研究，结合目前高速列车外地板的结构特征，对结构进行模态分析，对振幅最大的区域添加局域声子板，能很好的控制板的振动。

(2) 通过和试验验证确定商用软件仿真的准确度，结果证明在工程误差允许范围之内，得出了仿真的结果对实际的工程应用有一定的指导意义。

(3) 该方法将前处理、求解、后处理3个过程全部分开，通过分析不同情况下铝型材三角筋板的隔声情况，得到较优化的结果

(4) 通过在设置声场平面波的辐射，这种近似处理方法在低频有高度的拟合，但在高频复杂声场，误差度较大，对分析结果有一定的影响，所以需要对声场边界条件进一步的优化。

(5) 由于高速列车整车复杂的制造工艺，对降噪的措施还需进一步研究。

[1] 杨 弘.高速列车减振降噪技术研究[J].铁道车辆，2006，44(2): 9-14，45.

[2] Liu Z, Zhang X, Mao Y, Zhu Y Y, Yang Z, Chan C T, Sheng P. Locally resonant.

[3] 郑素贤,李道德,何延军.人-机-环境系统工程创立20周年纪念大会暨第五届全国人-机-环境系统工程学术会议论文集[C]. 2001.

[4] 赵艳菊，邓小军，林 鹏，等. 高速列车车体型材断面结构声学结构优化[J].铁道机车车辆,2017,32(1):40-44.

[5] Ding Y, Liu Z, Qin C, Shi J. Metanaterial with Simultaneously Negative Bulk Medulus and Mass Density[J]. Physical Review Letters, 2007, 99(9): 093904.

[6] Sheng P, Mei J, Liu Z, Wen W. Dynamic mass density and acoustic metamaterials[J]. Physica B. 2007, 394(2): 256-261.

[7] Milton GW, Willis JR. On modifications of Newton’s second law and linear continuum elastodynamics[J]. Proceedings of the Royal SocietyA. 2007, 463(2079): 855-880.

[8] Den Hartog.Mechanica Vibrations[M]. 4th ecl. New York,McGraw-Hill,1956.

[9] 张龙庆，朱胜阳，蔡成标，等. 动力吸振器在浮置板轨道低频振动控制中的应用[J].工程力学,2016(9):212-219.

[10] 马大猷. 噪声与振动控制工程手册[M]. 第1版. 北京：机械工业出版社, 2002.

[11] 肖 勇. 局域共振型结构的带隙调控与减振降噪特性研究[D]. 长沙：国防科技大学，2012.