体验中感悟让数学思想扎根——由一道期末试题引发对《数与形》的再思考

张丽萍

【教学过程】

一、自主探究，发现规律

1.出示杂乱的16个（4种不同颜色）小正方形。先让学生观察，并提出活动要求：（1）你能不能将这些小正方形重新分一分、摆一摆，让我们更加容易地看出小正方形的总个数？（2）想一想：根据你们的摆法可以写出哪个算式？

2.学生自主探究、摆拼。

（教师巡视、采样）

预设：

图1

图2（杂乱）

图3（规律）

反馈：

（1）看到图1你想到了哪个算式？你是怎么想的？

（2）同时出示图2和图3，它们有什么相同的地方？（都是正方形；都可以用4×4来表示等）

（3）你更喜欢哪一个图形，为什么？（更容易计算；在这个图形中既可以用4×4表示，也可以表示为 1+3+5+7）

（4）请学生上来指一指 1、3、5、7 分别在哪里；4×4 在哪里？

小结：它们都表示了边长为4的正方形里小正方形的总个数，得到等式：

1+3+5+7＝42。

3.引发思考：如果把拼成的正方形变小一些呢？变大一些呢？

重点反馈1+3+5+7+9=52。

（1）你想到了一个怎样的正方形？（边长为5）

（2）画一画，跟边长是4的正方形相比，增加的在哪里？（增加了9，约定把这个像拐角的数叫做“拐角数”）

图4

（3）随后依次得到：

1=12

1+3=22

1+3+5=32

1+3+5+7=42

1+3+5+7+9=52

1+3+5+7+9+11=62

……

学生自由表述规律，小结得出：连续奇数相加，有几个加数，就是几的平方。

5.引发冲突：3+5+7是否就等于32呢？

逐步完善，准确地表述规律：从1开始，连续奇数相加，有几个加数就等于几的平方。

【设计意图：通过操作活动和观察思考，引导学生发现数与形之间的规律，通过推理得到一般性结论，并进行准确表述。】

二、运用规律，解决问题

第一层次：1+3+5+7+……+（）=202

通过本题的解答，引导学生体验到运用刚刚发现的规律依次数到第20个奇数比较麻烦，而结合图形，就会发现拼成后的大正方形边长与最外层“┓”部分个数之间的关系，即┓＝边长×2－1。有了这条捷径，就能根据边长求出正方形最外层“┓”部分的数量，感受到数形结合方法的奇妙，加深学生对数形结合思想价值的感悟。

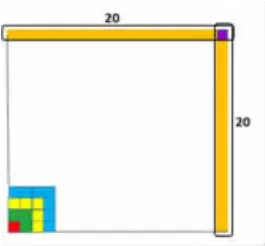
图5

第二层次：1+3+5+7+……+2017=（）2

高等职业院校教师应该采取主动学习和系统完善的策略，借用大数据这一平台了解和掌握当前在高职教育层面先进的教育教学方法，在提升教学方法多元性和功能性的前提下提升自身的教育教学质量。慕课、微课是当前高等职业院校中较为流行的教学形式，对于教师来讲要强化多元化先进教学形式和方法的应用，通过应用掌握慕课和微课等先进方法的开展形式与应用技巧，扩大高等职业院校教育教学的影响范围，进而为教育教学质量和效果的提升提供方法上和形式上的支持与保障。

在上一题解答的基础上，继续借助对图形的想象与思考，逆向思考，根据正方形最外层“┓”部分的数量求出拼成后的大正方形的边长，（2017+1）÷2即 2017加了1之后才是两条完整的边长，以形助数，直观简便。

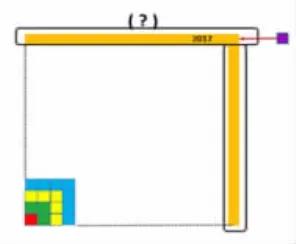
图6

第三层次：1002-992=（ ）

进一步巩固和深化对规律的认识，让学生感受到解决这样的问题，借助图形来想象和思考是一条简便的策略，边长为100的正方形中去掉一个边长为99的正方形，剩下的部分就是边长100的正方形最外面的┓！数形结合，问题就变得简单了！

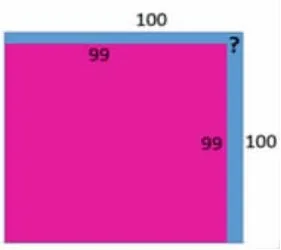
图7

【设计意图：进一步深化认识数与形之间的联系，巧妙地运用数形结合使复杂的问题简明化，解决起来更加简单，让学生进一步体会数形结合的奇妙与优越性。】

三、深化认识，感受价值

1.回顾过去学习过程中数形结合的例子。

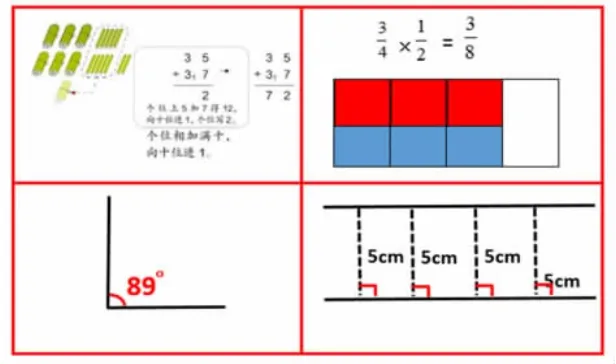
【设计意图：让学生体会到有了“数”的帮助，判断“形”时更加准确。】

2.知识拓展，感受运用数形结合理解印度乘法算理。

（1）出示印度人的乘法竖式，跟我们有什么不一样？（只有结果，没过程）

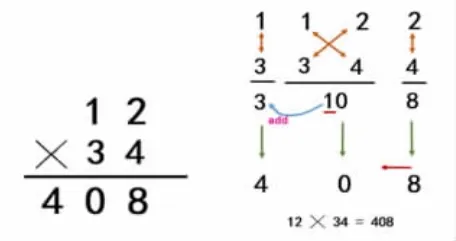
（2）继续出示：现在能看懂他们是怎么想的吗？（大部分学生看不明白，适时借助图形来理解印度乘法的算理）

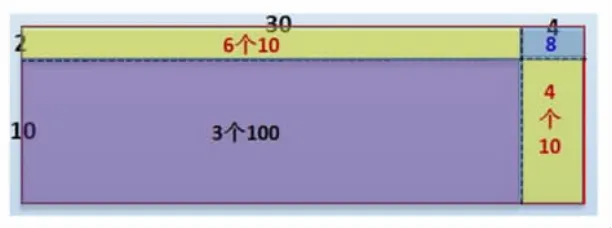
【设计意图：通过这个例子，让学生进一步体会到数形结合是一种常用的数学思想方法。】

四、课后挑战，巩固新知

出示97×96巧算过程，学生理解困难，自然想到借助图形帮助理解，由此布置课后作业：借助图形探究算理。

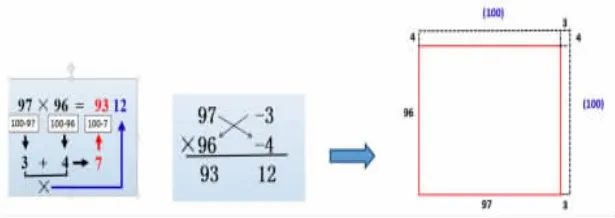
【设计意图：从一开始老师领着大家一起理解，到后来给出半成品的图让学生试着理解，再到最后由学生自主产生“以形助数”想法，由扶到放，举一反三，使学生认识到，数形结合并不只是这一课的任务，而是整个数学学习过程中重要的思想和方法，从而使数形结合的价值和思想在学生心中真正扎根。】

【教学思考】

2018年2月“嘉兴市小学数学六年级上册期末检测卷”中一道试题（如下图）：

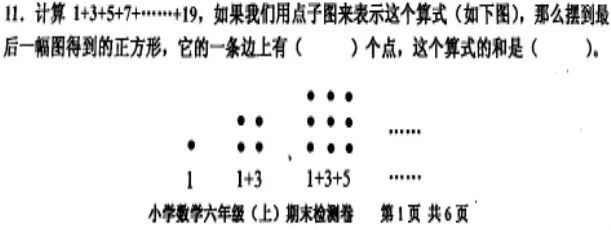
笔者对所在学校六年级三个班做了抽样调查，发现学生该题的得分率较低，数形结合不仅是一种解题方法，更是一种重要的数学思想，如何让学生在数学学习中体验数形结合思想，最终自觉地运用这种思想解决生活中的问题才是最根本的目标。由此，也引发了笔者对《数与形》一课的重新思考。

1.把握《课程标准》定位。

《课程标准》指出“数学是研究数量关系和空间形式的科学”。个人认为概括起来就是“数”与“形”的问题，通过几何直观可以帮助学生建立数的概念、理解数运算的意义，使解题思路与过程具体化。数形结合的方法可以让数量关系与图形的性质问题很好地转化。

2.研读教材意图。

《数与形》是修订版教材新增的内容。实验教材中，本内容以及后面编排的几道习题是供学有余力的学生学习和挑战的。现在作为例题编写，在教学中究竟该达到怎样的要求呢？纵观前面的教材，数形结合思想只是作为几何直观一条隐性线索加以渗透，并没有出现系统的教学，所涉及的练习也比较分散。到了六年级教材专门安排《数与形》一课，个人觉得是对“数形结合”这个数学思想方法的回顾和梳理，进一步让学生感受到“数形结合”思想方法的重要价值，提高学生用数形结合的思想解决问题的能力。

3.分析学生学情。

回顾学生五年多的学习，他们已经有了一些结合“形”来分析问题的基础。比如通过几何直观建立数的概念、理解运算的意义、明白解题的思路等等。因此，在进一步引导学生体会数与形之间联系的基础上，有必要引导学生回顾“数形结合”的内容，进行沟通，求得联系，在此基础上获得新的发展。

本课的重点应是使学生能自觉借助图形来解决相关数的问题，因此可把目标定为：使学生通过自主探究发现图形中隐藏着的数的规律，并能准确地表达规律和灵活地运用规律；使学生能自觉借助图形来解决相关数的问题；使学生在解决问题的过程中，体会数形结合的价值，掌握数形结合、归纳推理等基本的数学思想方法。而探究发现图形中隐藏着的数的规律，并能灵活地运用规律是需要突破的难点。