将数学思想与方法渗透于教学活动中
——《长方形与正方形》任务设计与教学
2018-05-10钟燕
钟 燕
《长方形与正方形》是小学数学“图形与几何”教学中的内容,北师大版教材把这一内容编排在二年级下册第六单元。长方形是平面几何中的一个基本图形,是后期学习各种几何图形的基础。本课学习任务设计主要围绕研究长方形的特征展开。
一、任务说明
1.任务及目标。
(1)学习任务。
①下面哪个图形是长方形,哪个不是?
②想象:把①号图形折成长方形。
③不动手折,借助直尺或三角尺把这条折痕画出来。想一想,怎样才能画标准?(挑战性任务)

(2)任务目标。
①结合观察、操作活动,能描述长方形的特征。
②了解折、画、比、量等多种认识图形的方法,体会研究图形方法的多样性。
③在探索长方形的特征中,激发对图形研究的好奇心。
2.设计说明。
关于长方形特征的认识,教材安排的操作活动(教材第67页)简单、直接,目标明确,通过操作学生能够顺利得出“长方形的对边相等,四个角都是直角”。但这一任务缺乏驱动力和挑战性,仔细分析,学生的操作并没有具体、明确的目标,只是按教师的指令进行操作,学生的探索活动并不需要深入思考,这样的学习任务无法在学生获取数学知识的同时,较好地发展他们的高层次认知能力。
我所设计的学习任务,把对长方形特征的认识融合于解决问题的过程中,需要学生积极主动参与,自主思考并选择解决办法。在操作、探索与体验的过程中,把握图形特征。任务设计经过反复实践,不断调整,主要经历了以下三次转变。
(1)从多到少,聚焦难点。

起初,设计了从十个图形中找出长方形的学习任务,并根据这些长方形展开探究。主要是考虑到图形的多样性有利于概念丰富性的建立,但是通过教学实践,我发现不是图形数量越多,就越能揭示长方形特征。图形数量过多,不利于交流互动。改进设计时,我将图形缩减为具有代表性的四个,分别是两个不同位置的长方形,一个直角梯形和一个平行四边形。将梯形和平行四边形通过折一折变成长方形,并将任务进行分层,先研究梯形,再研究平行四边形。在这个过程中,学生有任务、有观察、有动脑、有操作。但是在实践中又发现任务的两个层次并不明晰,过程有重复。最后确定留下三个图形,把直角梯形作为研究的重点材料,挑战性任务围绕直角梯形展开。聚焦难点,容易发现和捕捉学生个性化的解决问题的方法。
(2)从折到画,关注本质。

在学习任务1中,学生通过动手操作,将直角梯形折成长方形,这一过程中学生更多的是凭直觉操作,缺少对图形特征和解决问题策略多样性的思考。学习任务2,借助学生已有的折纸活动经验,重在引导学生思考如何画得标准,通过观察、想象、比较在脑中完成折的过程,并通过画折痕的方式把思考的成果物化下来,转化为展示、交流的资源。折和画看起来似乎只是两种不同的操作方式,其实有着较大的区别。区别之一:让学生画折痕突出了想象过程,有利于发展学生的空间观念;区别之二:让学生画折痕逼迫他们从定量的角度研究和把握长方形的特征。
(3)从正到斜,展现思维。
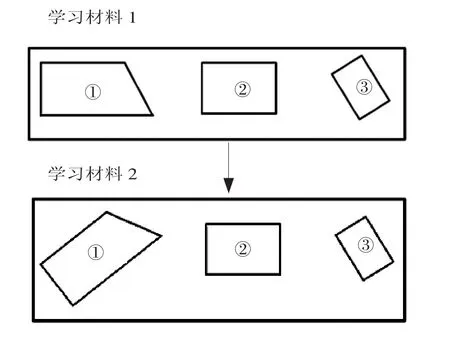
从两幅图的对比中可以发现,从材料1到材料2,直角梯形的摆放位置发生了改变。这一改变,使学生的关注点与思考方向发生了变化。材料1学生只要竖着画一条线段就可以,而材料2学生在操作时必须考虑所画的线段能不能与底边垂直,所产生的两组新的对边长度是不是相等。
实践中,材料摆放位置的简单变化,给教学带来了很大的变化。面对材料1,大部分学生都能较为准确地画出折痕,挑战性并不强。因为缺乏与错例的比较,在讨论“怎样才能画标准”时,学生不知道该如何回答。而面对材料2时,学生在画折痕前,有了更多的观察、思考,把梯形翻过去倒过来反复地揣摩。画好之后,学生之间的差异也非常明显,从结果来看,将近三分之一的学生画标准了,将近三分之二的学生存在问题。画好之后,很多学生能够自觉地应用各种方法对自己所画折痕进行验证。教学时,展现学生探索成果,比较差异,研究正误,能够引导学生深刻感知、掌握长方形特征,发展学生高层次认知能力。
二、任务教学
这一学习任务可以按以下教学程序展开:
首先,在黑板上呈现学习材料2中的三个图形,请学生观察后回答“哪个图形是长方形,哪个不是”,并说一说①号图形为什么不是长方形。再引导学生想象:把①号图形折成长方形。最后课件出示具有挑战性的学习任务:“不动手折,借助直尺或三角尺把这条折痕画出来。想一想,怎样才能画标准?”在学生明确任务要求后,独立尝试解决。
在学生解决问题过程中,教师需要巡视并收集学生操作的成果。教学反馈时,教师应把重点放在引导学生讨论“如何验证是否画得标准”上,可以选择并投影呈现两幅学生作品,一幅标准的,一幅略微有偏差的。先引导学生观察、想象、比较,发现无法进行清晰辨别。在学生愤悱之时,提出问题:“哪幅画得更标准,你有什么好办法来验证?”学生思考、交流解决问题的过程,就是学生研究长方形边和角的特征的过程。
上述任务设计不仅有学生喜爱的看一看、画一画等具体的活动,同时又能引导学生通过观察、辨别、测量、对比、抽象、概括,把直观几何和抽象推理、逻辑演绎、严格证明的方式相结合,有力地促进数学知识在活动中的内化,从而掌握图形的特征。把数学思想与方法渗透于教学活动中,有效提升学生的数学素养,发展高水平认知能力。
