一题三妙解

涂 勇

(湖北省宜都市二中 443311)

在物理学习中，经常开展或尝试“一题多解”，有助于拓宽思维、加深对知识和规律的理解，又能起到“一题多用”提高试题利用效率、走出“题海战术”的误区的作用.下面列举一例，希望有抛砖引玉之效.

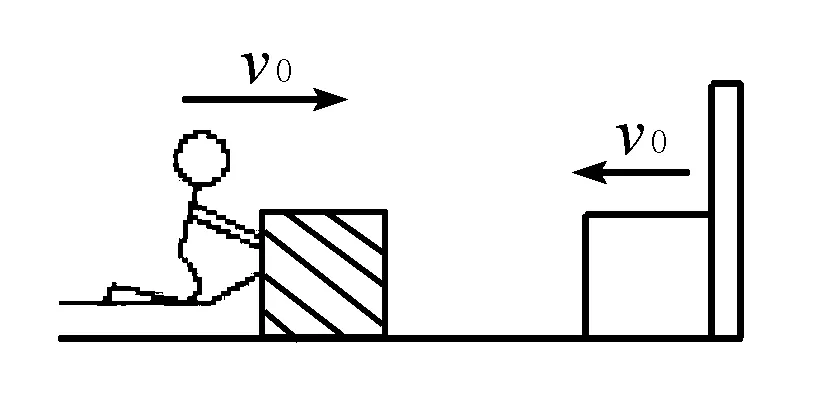
例题如图所示，人与冰车的总质量为M，另有一质量为m的坚固木箱，M∶m=31∶2，开始时人坐在冰车上静止于光滑水平冰面上，某时刻人将静止的木箱以相对冰面的速度v0向右推向挡板，同时冰车反向滑动，木箱与挡板碰撞后又反向弹回，且碰撞过程无机械能的损失，人接到木箱后再以速度v0推向挡板，如此反复，求人推木箱多少次后不能再接到木箱？

分析人与冰车是一个整体，箱子与人、与挡板反复作用往返运动，情景复杂.而解力学问题可供选择的方法有：动力学思维、能量思维和动量的思维方法；动力学思维是分析力学问题的基础，对于复杂的力学情景，优先选择能量或动量的方法解题.本题涉及反复推、撞的速度而不涉及位移，即不考虑作用力做功，所以选用动量的方法解题.

解法一对人、冰车和木箱系统用动量定理求解

以人、冰车和木箱系统为研究对象，系统竖直方向受力平衡，挡板对箱子的作用力即为系统外力的合力，挡板对箱子的反复碰撞，使系统动量不断增加.取水平向左的方向为正方向，箱子每次与挡板作用，速度由-v0变为v0.

P1=0 ①

根据动量定理，箱子每次与挡板作用受冲量为：

I=mv0-m(-v0)=2mv0②

第n次推出后人车速为vn，箱子速度-v0，则人车与箱子动量的矢量和为：

Pn=Mvn-mv0③

第n次推时，箱子与挡板碰撞了(n-1)次，系统受到总冲量为：

I总=(n-1)I=2(n-1)mv0④

对系统用动量定理得:

I总=Pn-P1=Mvn-mv0⑤

设第n次推出后人不能再接到箱子，则有：

vn≥v0⑥

代入数据得：n≥8.25，取n=9，即人推出9次后，再也接不到箱子.

解法二对人、冰车和木箱系统用动量守恒定律求解

以人、冰车和木箱系统为研究对象，由于挡板对箱子的作用力为系统外力，则系统动量不守恒，如取箱子在每一次接、推前后的过程来研究，系统动量守恒，设每次推出后冰车速度分别为v1、v2、v3……vn，取水平向左为正方向，根据动量守恒定律有：

第一次推前后：0=Mv1-mv0

第二次推前后:Mv1+mv0=Mv2-mv0

同理，第三次有：Mv2+mv0=Mv3-mv0

……

第n次推前后：Mvn-1+mv0=Mvn-mv0

将各式叠加求和有：(n-1)mv0=Mvn-nmv0

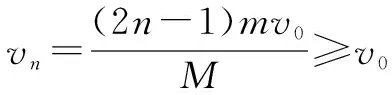
代入数据得：n≥8.25，取n=9.

解法三对人冰车整体用动量定理求解

人与冰车可视为一个物体.人每次推箱子推力的冲量为I1、I2、I3…In，总冲量I，取水平向左方向为正方向，对箱子用动量定理有:

第一次由静止推，推力冲量：

I1=ΔP1=-mv0-0=-mv0

由于挡板将箱子弹回无能量损失，箱子弹回速度为v0，每次接推箱子，箱子的速度由v0变为-v0，所以有：

I2=ΔP2=-mv0-mv0=-2mv0

I2=I3=…=In

人推箱子n次，推力的总冲量为:I=I1+I2+I3…+In=-(2n-1)mv0

由于人推箱子的力F与箱子推人的力F′互为作用力与反作用力，即F′=-F，且两力的作用时间相同，所以箱子对人冲量I'与人对箱子冲量I等大反向：

I′=-I=(2n-1)mv0

对于人冰车原来静止，初动量P=0；推n次时，人车速度vn，动量P′=Mvn，根据动量定理有：

I′=P′-P=Mvn-0=(2n-1)mv0

箱子弹回时人接不到箱子的条件是：vn≥v0，代入数据解得：n=9.

评析纵观三种解法，以系统为研究对象，动量守恒与否不是绝对的，与对应的物理过程的选取有关，灵活处理物理过程适用相应的物理规律是解题的妙之所在；动量定理多用于单一物体，对系统使用很少见，两种用法对比出现，可开拓学生视野；其次灵活妙用数列递推式，是解题的另一关键.一题多解，涵盖了动量全章的知识和规律：冲量、动量、动量定理和动量守恒定律，复习知识训练能力效率高.

参考文献：

[1]人教社.高中物理人教版教课书选修3 - 5.动量守恒定律[M].北京：首付师范大学出版社，2009.