厚原子蒸气介质中原子选择性光电离的理论研究

卢肖勇 张小章 张志忠

1)(清华大学工程物理系,北京 100084)

2)(核工业理化工程研究院,天津 300180)

(2017年10月29日收到;2018年1月24日收到修改稿)

1 引 言

原子的选择性光电离是原子蒸气激光同位素分离中关键的一步,因为它直接影响分离过程的选择性和目标同位素的利用率.为了提高激发电离效率以及电离过程的同位素选择性,科研人员对其中的原子选择性光电离过程开展了大量的理论研究[1−7].这些研究中通常将原子蒸气看作是光学薄介质,也就是认为原子蒸气介质对激光脉冲没有影响.然而在实际的激光同位素分离过程中,原子蒸气的密度以及激光在作用区内传输距离都是比较大的.实验结果表明,脉冲激光通过光学厚原子蒸气过程中不仅功率会发生显著变化,同时还有脉冲延迟和脉冲变形[8−13],因此将原子蒸气视作光学薄介质来处理光电离过程是不合适的.为了从理论上更有针对性地开展研究,必须将原子蒸气视为光学厚介质,在考虑它对脉冲激光影响的条件下研究光电离过程则更具实际意义.

有一些研究考虑了厚介质条件下的电离过程,但是大多只考虑了原子蒸气中的目标同位素[14−17],主要关注了激光传播路径上激光脉冲的演化和空间单点电离率的变化[18−21],缺少对整个厚介质中平均电离率和选择性的研究,这是激光同位素分离理论研究的一个不足之处.本文考虑了光学厚介质中两种同位素的吸收过程对脉冲激光的影响,并计算了原子蒸气中不同位置处激光脉冲形状、两种同位素的电离率和电离选择性.在此基础上,研究了原子蒸气的平均电离率和平均选择性随激光参数和原子蒸气参数的变化趋势,并对上述参数给出了优化方向.

2 数学理论模型

图1为原子三步光电离模型,同位素A为目标同位素,同位素B为非目标同位素,原子受到3束激光的作用.前两束激光可以将原子从基态激发到第2激发态,第3束激光将原子激发到电离限之上的连续能区,使原子电离.由于原子的第3步激发过程涉及连续态或者多电子激发,所以在本文采用的密度矩阵方法中进行了唯像处理.激光1,2与同位素A的能级跃迁共振,由于同位素位移的存在,这两束激光对同位素B的激发是失谐的.设两束激光沿着z方向传播,其光场可以表示为

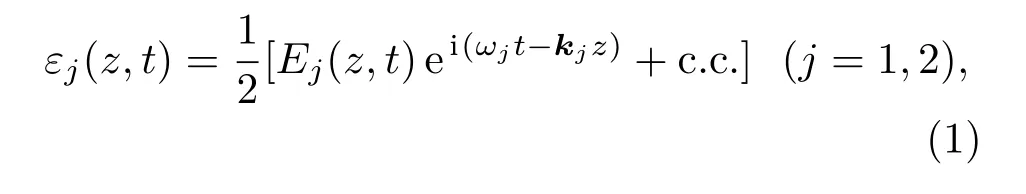
式中Ej(z,t)为激光场的复振幅;ωj为激光的圆频率;kj为波矢.

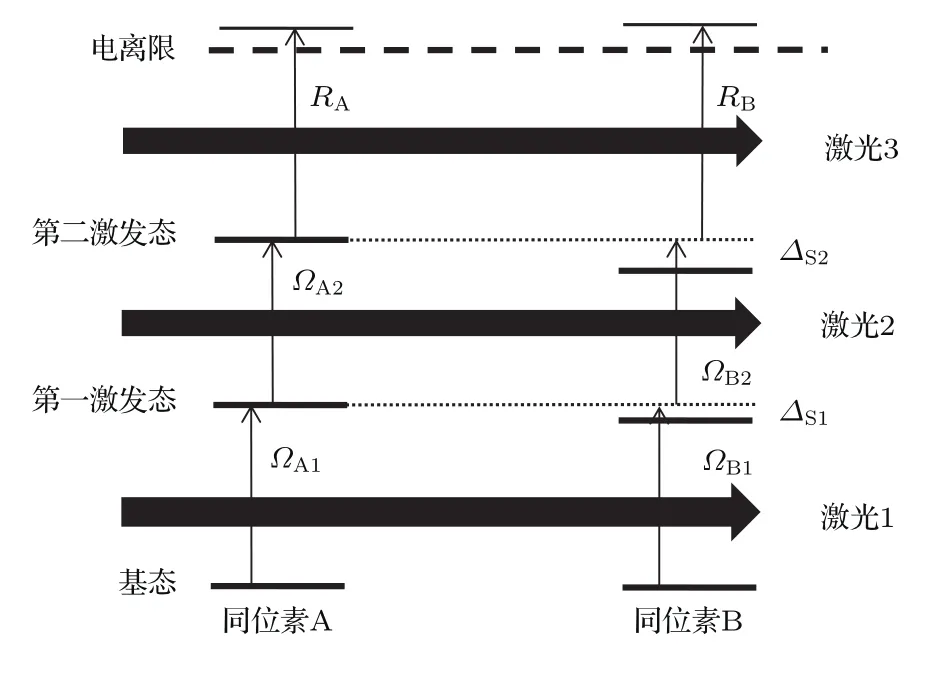
图1 原子三步光电离路径图Fig.1.Schematic diagram of three-step photoionization of atom.

根据文献[1],对电离跃迁做唯像处理之后,可以得到光传播路径上任意位置z处原子三步光电离的密度矩阵方程组为:

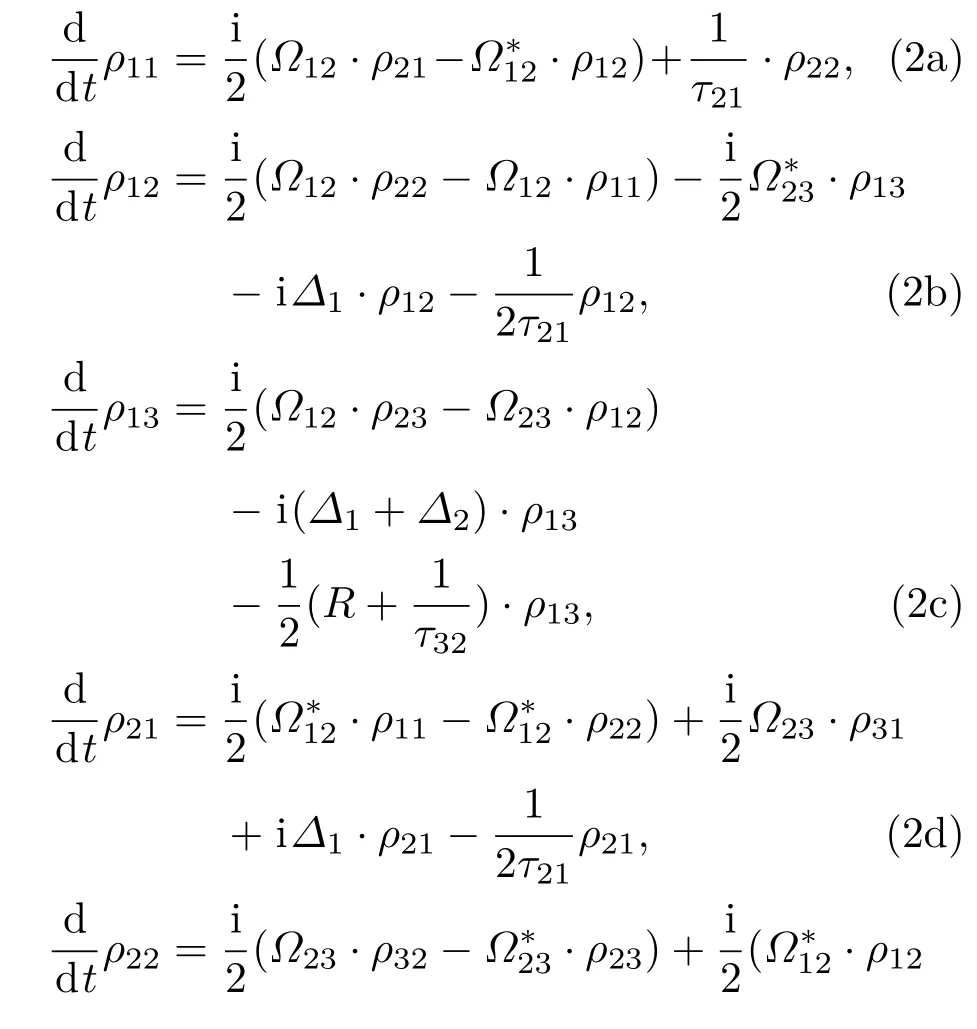
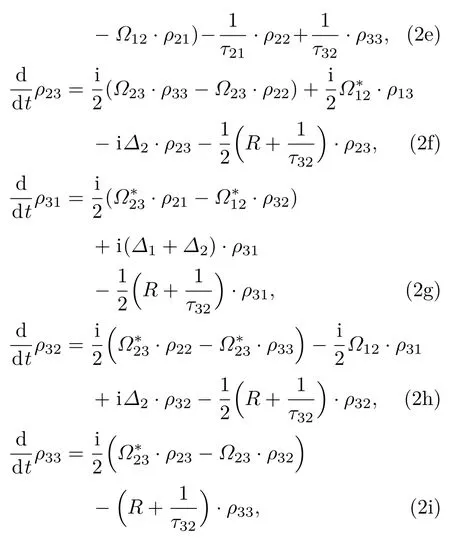
式中ρmn(m,n=1,2,3)为密度矩阵元;∆1和∆2为第1步和第2步跃迁的激光失谐量;τ21和τ32分别为第一激发态和第二激发态的自发辐射寿命;R为电离速率;Ω12和Ω23为第1步和第2步跃迁的Rabi频率,其表达式为

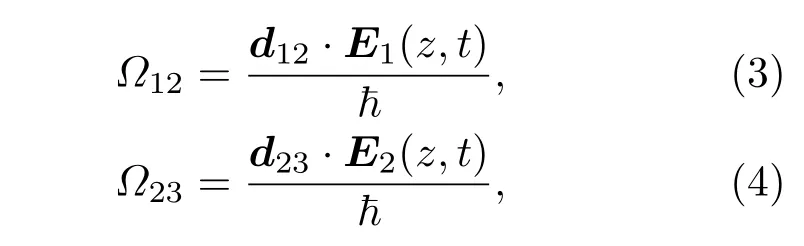
其中d12和d23为原子跃迁的电偶极矩.(2a)—(2i)式表示成矩阵形式则为

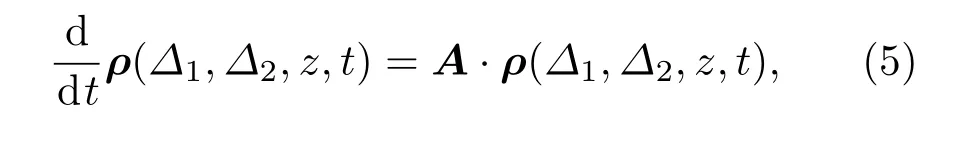
式中ρ(∆1,∆2,z,t)=[ρ11ρ12···ρ33]T,对于原子蒸气中存在A,B两种同位素的情况,A和B跃迁的动力学方程分别为:

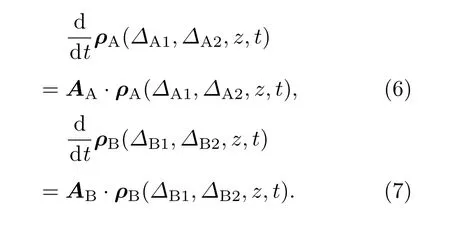
激光场在原子蒸气介质中的传播采用慢变振幅近似下的Maxwell方程描述[9]:

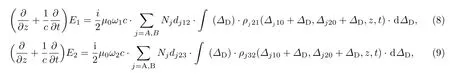
式中µ0为真空磁导率;ω1,ω2分别为两束激光的圆频率;c为真空光速;Nj(j=A,B)为两种同位素的原子数密度;∆j10和∆j20为激光失谐量,是原子吸收谱线中心波长与激光波长的差;f(∆D)为原子吸收谱线的线型函数,∆D为原子吸收谱线的Doppler展宽.取延时坐标,做如下变换:t′=t−z/c,ξ=z,则(6)—(9)式变为

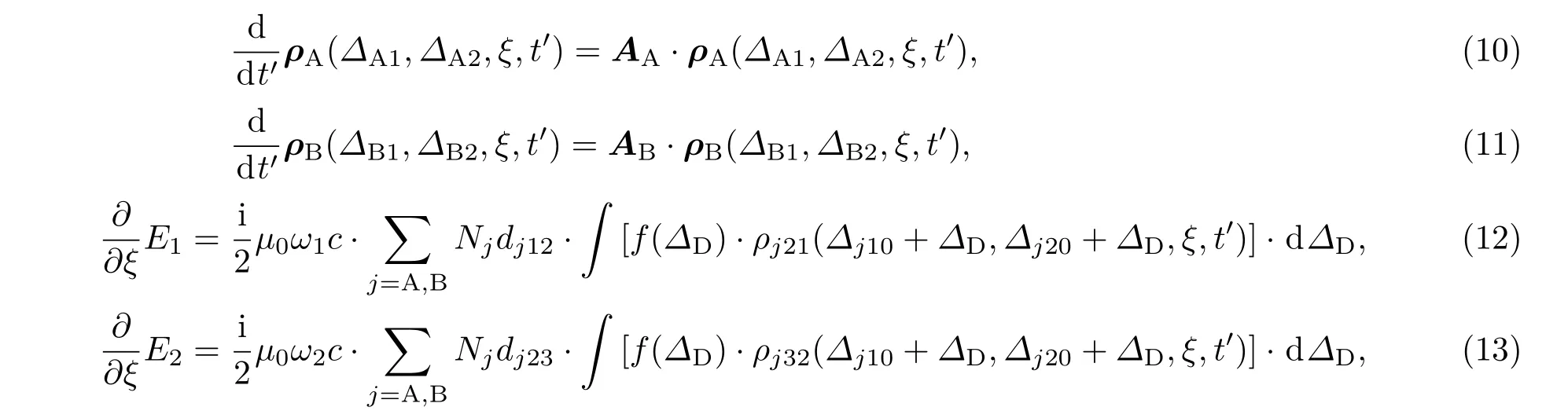
(10)—(13)式即为激光在原子蒸气介质中传播的耦合方程组.一般情况下,(10)—(13)式方程组无法求得解析解,因此本文采用数值方法求解.对密度矩阵方程(10)式和(11)式用4阶Runge-Kutta方法求解,对Maxwell方程(12)式和(13)式采用预报校正方法求解[22,23].

设t0时刻两束激光脉冲均完全穿越原子蒸气,则原子蒸气中不同位置ξ处同位素A,B的电离率由(14)式得到

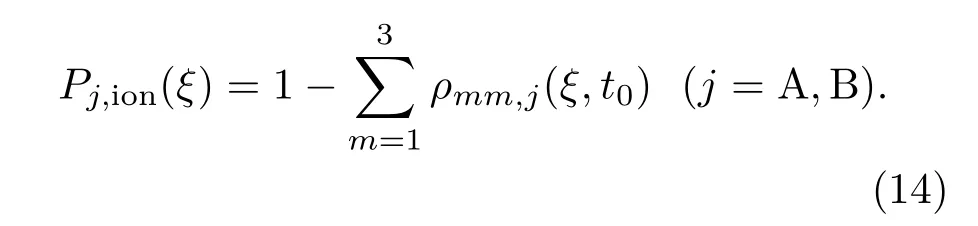
对于厚度为L的原子蒸气介质,其平均电离率Pj,ion和平均选择性S计算式分别为

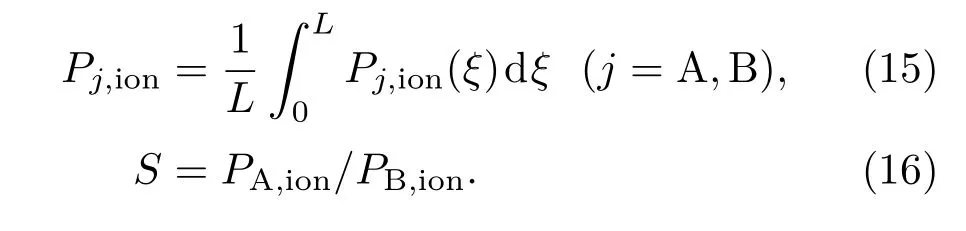
3 结果与讨论

在以下的计算结果中,如不做额外说明,均使用以下计算参数:同位素A原子密度NA=1.0×1018m−3;两步跃迁的偶极矩dA12=1.0×10−30C·m,dA23=1.0×10−30C·m;第一激发态和第二激发态寿命分别为40 ns和100 ns;电离速率RA=0.2×109s−1,同位素B和同位素A的以上参数相同.原子吸收谱线的Doppler展宽为600 MHz.两步激光波长均取为500 nm,脉宽30 ns,激光脉冲的形状为Gauss型,其峰值对应的电场强度均为2.0×105V/m,两束激光之间无延时.两束激光与同位素A共振,与同位素B两个跃迁的失谐量分别为∆S1=2.0 GHz,∆S2=2.0 GHz.

图2为不同传播距离处的激光脉冲形状.图3表示在图2的计算条件下,不同传播距离处两种同位素的电离率及该处的选择性.从图2可以看出,两束脉冲在介质中的损耗情况存在差异:第一,原子的第1步跃迁先于第2步跃迁,因此随着传播距离的增加,第1束激光的损耗集中在脉冲的前端(图2中激光脉冲左侧),第2束激光的损耗主要集中在后端;第二,光电离过程中原子在基态和第一激发态布居数的不同,原子蒸气介质对两束激光的折射率存在差异,这导致第1束激光在介质中的传播速度小于第2束激光.上述两个过程共同作用使两束激光在传播过程中产生相对延时,激光的激发强度减弱,最后导致了两种同位素的电离率下降.由于非目标同位素是失谐激发的,这种电离率下降对非目标同位素更为明显,所以选择性反而会升高.当两束激光在时间上完全分开后,如图2中7 m之后的位置,第一激发态自发辐射会造成第1束激光的损耗,第1束激光脉冲在介质中传播时逐渐损耗并消失,第2束激光脉冲则相当于在真空中传播,脉冲形状不发生变化,电离率降为0.

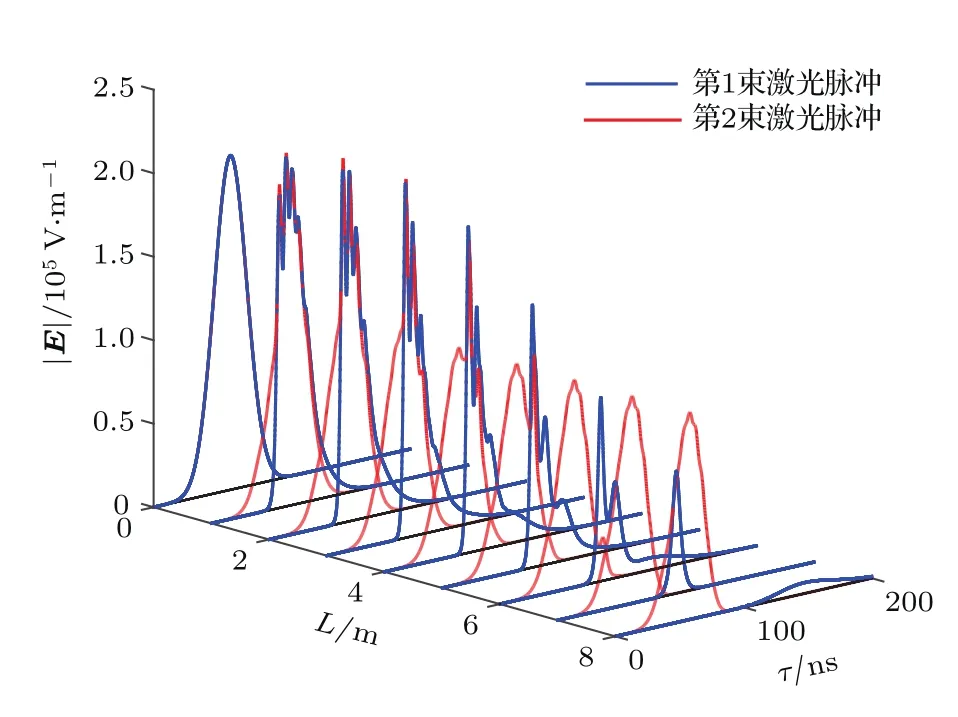
图2 激光脉冲形状在原子蒸气介质中的演化Fig.2.Evolution of laser pulse shape in a thick atom vapor medium.

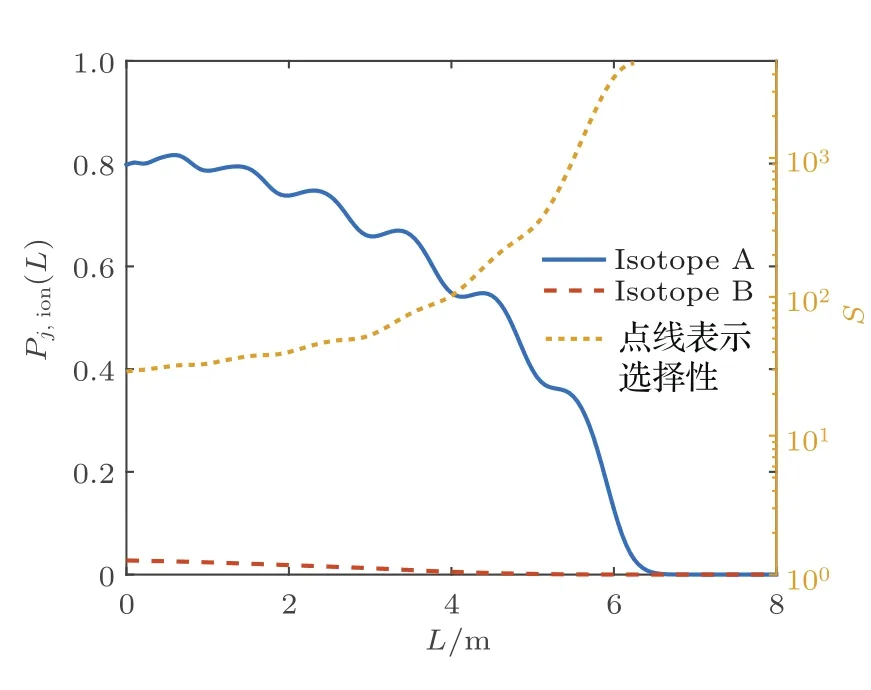
图3 电离率和选择性随空间位置的变化Fig.3.Variation of ionization yield and selectivity with space distribution.

图4 为第1束激光强度取不同值时,原子的平均电离率(此处的平均电离率均指同位素A的平均电离率,下同)和平均选择性随原子蒸气厚度的变化曲线.设定平均选择性停止增加的位置为激光的有效电离长度(见图4箭头).可以看出,随着激光强度的增加,两束激光在更长的传播距离内保持同步,其有效电离长度增加.对于较厚的原子蒸气,平均电离率随着激光强度的增加而增加;而对于相对较薄的原子蒸气,比较图4(a)中的3条曲线可以发现,第1束激光强度的增加则使平均电离率下降,这是因为激光过强会引起原子在基态和第一激发态之间快速的布居振荡,影响了后续的激发电离过程,当第2束激光的光强很大时也有此现象[3,19,24].而随着激光线宽和原子吸收谱线Doppler展宽的增加,这种现象会逐渐减弱至消失.因此,当原子蒸气的厚度相对较小时,选择低的激光强度有利于同时获得高的平均选择性和平均电离率,而对于激光同位素分离中的厚原子蒸气介质,激光功率的增大可以提高原子的电离率,但是会使光电离的选择性下降.

图5为原子蒸气厚度一定时(L=8 m),两种同位素的平均电离率和平均选择性随两束激光脉宽的变化曲线(单个激光脉冲的能量保持不变).可以看出,随着激光脉宽的增大,同位素A的平均电离率有小幅度提高,而同位素B平均电离率的下降则十分明显,这是因为随着激光脉宽的增加,脉冲作用时间内的激光功率下降,由于同位素A原子为过饱和激发,功率下降对其激发电离速率影响不大,脉冲宽度的增加则可以提高激发电离过程的时间,因此电离率升高,对于光学薄介质亦有此现象[25,26];而同位素B由于为非共振激发,对脉冲作用时间内的功率下降更为敏感,因此其电离率下降,相应的平均选择性有较大幅度的提高.因此在光电离过程中应尽量增加激光脉冲宽度.

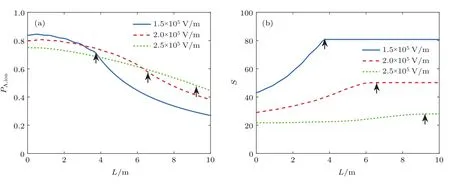
图4 (a)平均电离率和(b)平均选择性随原子蒸气厚度的变化Fig.4.Variation of(a)average ionization yield and(b)average selectivity with thickness of atom vapor.

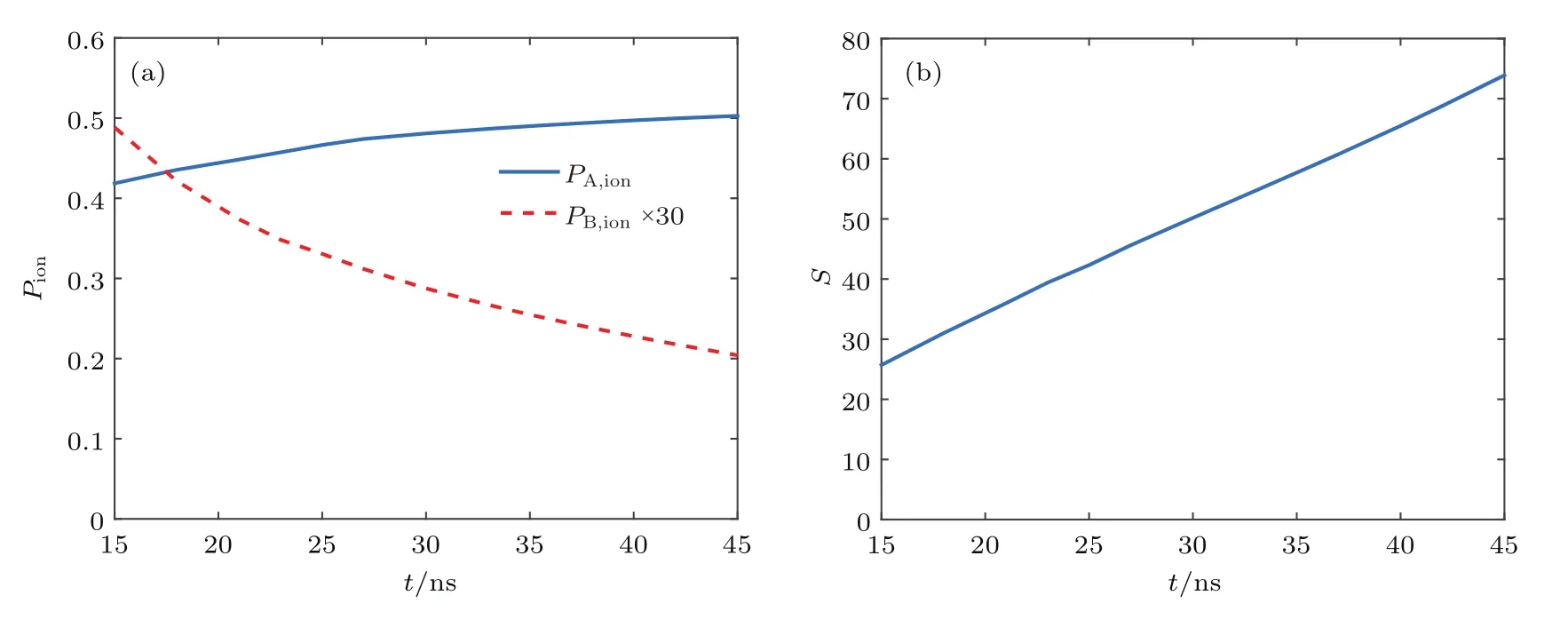
图5 (a)平均电离率和(b)平均选择性随激光脉宽的变化Fig.5.Variation of(a)average ionization yield and(b)average selectivity with laser pulse width.

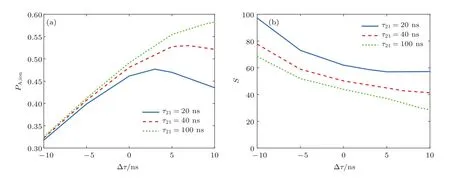
图6 (a)平均电离率和(b)平均选择性随激光延时的变化Fig.6.Variation of(a)average ionization yield and(b)average selectivity with laser pulse time delay.

图6 为原子蒸气厚度一定(L=8 m),当第一激发态寿命取不同值时,同位素A的平均电离率和平均选择性随激光延时的变化曲线,假设第1束激光相对第2束激光超前时延时为正.从图6中可以看出,存在一个最佳正激光延时,使同位素A原子的平均电离率达到最大.这是因为随着激光延时的增大,第2束激光脉冲前端的能量也得到利用,且由于第1束激光脉冲的传播速度小于第2束激光脉冲,有效电离长度增加,因此同位素A的平均电离率增加;当激光延时继续增大,则第1束激光脉冲的前端仅使原子在基态和第一激发态间做Rabi振荡,直到第2束激光到来时才会有后续的激发电离过程,这相当于第1束激光的有效强度减弱了,因此平均电离率下降.与已发表的薄介质中激光延时对电离过程影响的文献[27,28]相比较发现,为了获得更高的电离率,薄介质光电离过程中激光延时的设置可以使更多的原子处于高激发态;而厚介质中激光延时的设置则更多地考虑到传播路径上两束光的同步传播.且最佳正激光延时随着原子第一激发态寿命的增加而增加.图6(b)则显示平均选择性随着激光延时的变化趋势与平均电离率相反.因此在光电离过程中,应当综合考虑目标同位素的电离率和选择性两方面来选择合适的激光延时.

图7为原子蒸气厚度一定(L=8 m),当两束激光的脉冲宽度取不同值时,同位素A的平均电离率和平均选择性随激光延时的变化曲线.从图7中可以看出,随着激光脉宽的增加,同位素A的平均电离率和平均选择性得到了同时提高,且当激光延时为负值时,平均电离率的提高尤为明显.另外,从图7(a)中也可以看出,激光脉宽的增加也使平均电离率随延时变化的曲线变缓、最佳激光延时增大.这说明在实验时增加激光的脉冲宽度,不仅有利于同时提高平均电离率和平均选择性,还可以降低对激光脉冲之间相对延时的控制精度.

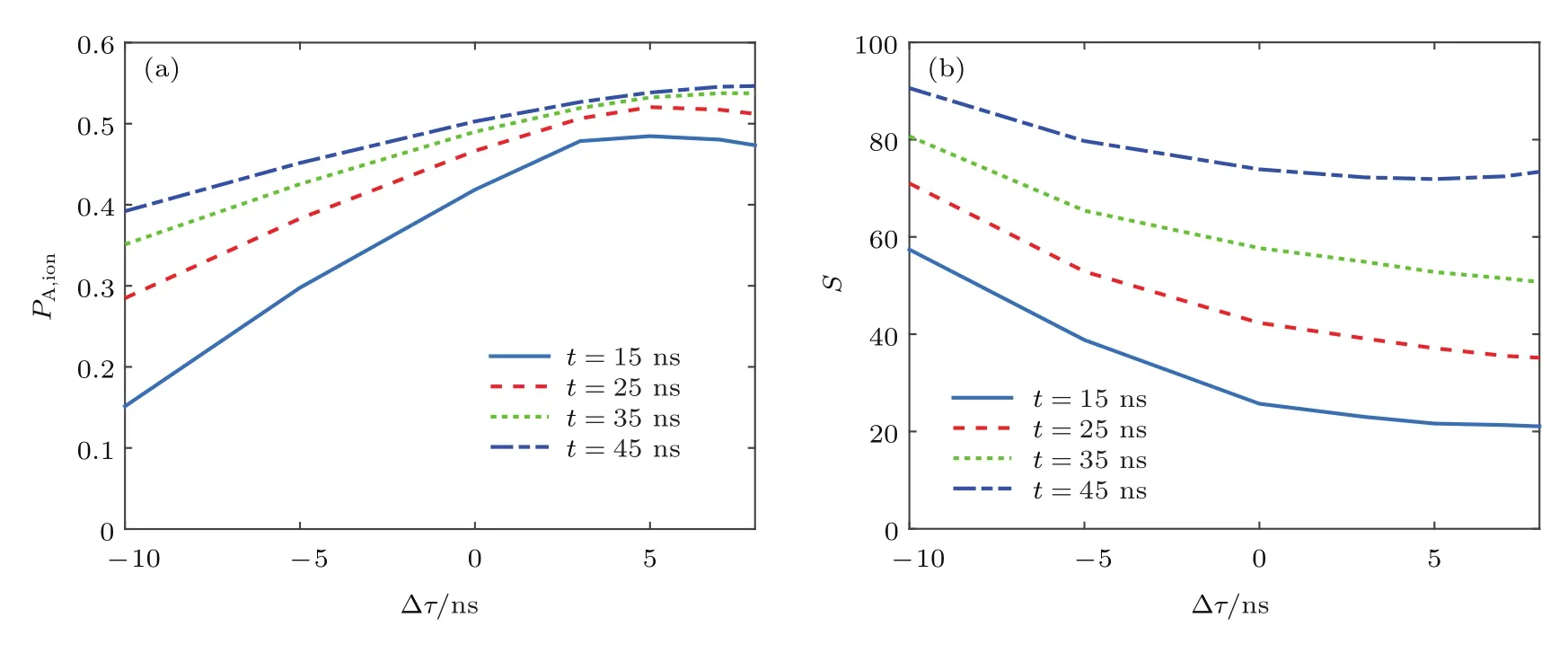
图7 不同激光脉宽下(a)平均电离率和(b)平均选择性随激光延时的变化Fig.7.Variation of(a)average ionization yield and(b)average selectivity with laser pulse time delay for dif f erent laser pulse widths.

4 结 论

在考虑厚原子蒸气介质中同时存在的两种同位素都与激光有相互作用的情况下,对厚介质中目标同位素的平均电离率和平均选择性进行了计算,得到了如下的结论:两束同时发射的激光脉冲在介质中传播时会产生相对延迟,导致在激光传播路径上,原子蒸气单点的电离率下降,选择性升高.对于较厚的原子蒸气介质,增加激光功率可以使平均电离率升高,但是平均选择性则会下降;对于较薄的介质,适当地降低激光功率则可以同时提高平均电离率和平均选择性.在原子蒸气参数不变的条件下,存在一个正的激光延时使平均电离率达到最大,平均选择性随激光延时的变化趋势则与电离率相反.另外,固定单个激光脉冲的能量,尽量延长激光脉冲的宽度不仅可以同时提高目标同位素的平均电离率和平均选择性,还可以降低对激光脉冲之间相对延时的控制精度.

[1]Wang D W 1999Theory and Application of Laser Isotope Separation(Beijing: Atomic Energy Press)pp167–170(in Chinese)[王德武 1999激光分离同位素理论及其应用(北京:原子能出版社)第167—170页]

[2]Yuan K X,Yu C J 1994J.Atom.Mol.Phys.11 71(in Chinese)[袁奎训,于长江 1994原子与分子物理学报 11 71]

[3]Fan F Y,Wang L J 2011Acta Phys.Sin.60 093203(in Chinese)[范凤英,王立军 2011物理学报 60 093203]

[4]Qi X Q,Wang F,Dai C J 2015Acta Phys.Sin.64 133201(in Chinese)[戚晓秋,汪峰,戴长建2015物理学报64 133201]

[5]Saleem M,Hussain S,Rafiq M,Baig M A 2006J.Appl.Phys.100 053111

[6]Wang L J,Yu H Y 2004Acta Phys.Sin.53 4151(in Chinese)[王立军,余慧莺 2004物理学报 53 4151]

[7]Das R M,Chatterjee S,Iwasaki M,Nakajima T 2015J.Opt.Soc.Am.B32 1237

[8]Siddons P 2014J.Phys.B:At.Mol.Opt.47 093001

[9]Li fl2006Advanced Laser Physics(Beijing:Higher Education Press)pp128–138(in Chinese)[李福利 2006高等激光物理学(北京:高等教育出版社)第128—138页]

[10]Nomaru K,Izawa Y,Nakai S,Chen Y W,Yamanaka C 1994J.Nucl.Sci.Technol.31 914

[11]Nomaru K,Izawa Y,Nakai S,Chen Y W 1997J.Nucl.Sci.Technol.34 1147

[12]Yi J,Park H,Rhee Y,Lee J 2000Jpn.J.Appl.Phys.39 1128

[13]Ji W,Wu C,Raymer M G 2007J.Opt.Soc.Am.B24 629

[14]Jiang M H,Lin F C 1990Acta Phys.Sin.39 1887(in Chinese)[蒋孟衡,林福成 1990物理学报 39 1887]

[15]Xiao L,Lin F C 1998Acta Opt.Sin.18 1001(in Chinese)[肖玲,林福成 1998光学学报 18 1001]

[16]Chen Y W,Izawa Y,Nakai S,Yamanaka C 1995Jpn.J.Appl.Phys.34 504

[17]Xuan K D,Minh D H,Van D L,Huy B N 2017Optik131 497

[18]Jiang M H,Lin F C 1991Acta Opt.Sin.11 769(in Chinese)[蒋孟衡,林福成 1991光学学报 11 769]

[19]Xie S L,Wang D W,Ying C T,Zhu X H 1998Chin.J.Laser25 65(in Chinese)[谢世亮,王德武,应纯同,诸旭辉1998中国激光25 65]

[20]Xiao L,Lin F C 1999Acta Opt.Sin.19 1009(in Chinese)[肖玲,林福成 1999光学学报 19 1009]

[21]Chen Y W,Yamanaka C,Niki H,Adachi S,Izawa Y,Nakai S 1994J.Opt.Soc.Am.B11 1585

[22]Zhang H R,Li C,Yu X Y 2010Acta Phot.Sin.39 6(in Chinese)[张华荣,李成,余向阳 2010光子学报 39 6]

[23]Li C,Zhang H R,Yu X Y 2009Acta Sci.Nat.Univ.Sunyatseni.48 36(in Chinese)[李成,张华荣,余向阳2009中山大学学报(自然科学版)48 36]

[24]Xie S L,Wang D W,Ying C T 1997Chin.J.Nucl.Sci.Eng.17 166(in Chinese)[谢世亮,王德武,应纯同 1997核科学与工程17 166]

[25]Lu B S,Cui Z F 1998J.Atom.Mol.Phys.15 553(in Chinese)[卢秉嵩,崔执凤 1998原子与分子物理学报 15 553]

[26]Wang X L,Yao G X,Zhang X Y,Xu X S,Feng E Y,Ji X H,Cui Z F 2005Chin.J.Laser32 1211(in Chinese)[汪小丽,姚关心,张先熠,许新胜,凤尔银,季学韩,崔执凤2005中国激光32 1211]

[27]Liu B,Ning X J 2001Phys.Rev.A64 013401

[28]Li Z M,Zhu F R,Deng H,Ren X J,Zhai L H,Wang C H,Zhang L X 2006J.Atom.Mol.Phys.23 185(in Chinese)[李志明,朱凤蓉,邓虎,任向军,翟利华,王长海,张利兴2006原子与分子物理学报23 185]