等离子体中散斑光场的传输特性

杨春林

(成都精密光学工程研究中心,成都 610041)

(2017年8月6日收到;2018年2月7日收到修改稿)

1 引 言

激光驱动惯性约束核聚变(ICF)系统中,激光与等离子体的相互作用是决定聚变点火成败的一个关键环节[1−3].当激光在等离子体中传输时,等离子体可以通过两种不同的机制来吸收激光能量.一种是正常吸收,也称为逆韧致吸收,这是等离子体中的电子受激光场加速时,在等离子体的离子库仑场附近散射引起的经典吸收过程[4];另一种则是反常吸收,其结果将导致各种等离子体不稳定性过程的产生[5−8].在激光打靶中,关注的不稳定性过程主要有受激拉曼散射[9−13]、受激布里渊散射[14]、双等离子体衰变、成丝不稳定性、离子声衰变、共振吸收[15]等.这些不稳定过程会激发大量离子声波和电子等离子体波等,这不仅损失了相当份额的激光能量,而且离子声波和电子等离子体波会导致部分电子和离子的加速,使其形成对激光聚变中的内爆压缩过程有害的超热电子和高能离子,因此需要对各类不稳定性过程进行抑制.

根据美国劳伦斯利弗莫尔国家实验室(LLNL)的研究结果,降低激光的相干性对抑制等离子体不稳定性具有显著作用,因此国内外相关研究机构都在这一方向开展了大量研究工作,且主要对等离子体中高斯光束的传输以及各种激光等离子体的非线性效应进行了分析.

但实际上激光驱动装置目前普遍采用的是散斑打靶方式,也就是在激光装置终端加入连续位相板(CPP)元件以产生散斑来抑制非线性效应.由此可见,实际上与等离子体的产生相互作用的是一个散斑光场,而非通常研究使用的高斯光束.两种光场的特性完全不同,因此现有分析模型对这一现象的描述存在不足.早期光学散斑的研究由Goodman[16]发展并完善起来,他推导了散斑横向和纵向自相关函数,描绘出了散斑的基本图样.不过他在分析中假设产生散斑的光学元件的自相关函数是δ函数,这在实际的元件设计与加工中是不可能的,且标准的统计光学理论也没有包含等离子体介质的传输.因此,有必要针对实际的散斑光场与等离子体之间的相互作用建立一个新的分析模型.

本文基于矩阵光学理论[17]和Collins公式,提出了一个分析等离子体中散斑线性传输的理论模型,推导了等离子体的ABCD光学传输矩阵,并对该介质中的散斑光场特性进行了分析计算.结果表明,在等离子体中传播的散斑光场的自相关长度比空气(或真空)中的短.散斑光场有限的纵向自相关是它与平面光和高斯光束的最重要的区别,能破坏位相匹配和非线性积累,也就破坏了激光等离子体的非线性作用,且自相关长度越短越好.这就解释了CPP的作用机理,并为进一步研究等离子体非线性和抑制各种不稳定性提供了技术支撑.

2 散斑光场的传输理论

如图1所示,在ICF系统中,为消除相干性,在光路终端会使用CPP元件来产生散斑.当光传输到焦点附近,会遇到靶面产生的等离子体介质,光束聚焦过程中将通过真空和等离子体两种不同的介质,这使聚焦过程变得复杂了.在分析这种复杂的传输过程时,Collins公式是一种很有效的工具.设输入光场为E(x1,y1)=exp{jφ(x1,y1)},通过Collins公式可以得到靶面散斑光场:

其中K是一个和积分变量无关的常位相因子;E是光场复振幅;x1,y1是入射面坐标;x2,y2是靶面坐标;A,B,D三个参数是光学传输矩阵的对应元素.从(1)式中可以看出,这里计算时只包含了其中的A,B和D元素,而元素C没有被Collins公式使用.将输入光场表达式代入,就可以直接计算得到散斑在传输方向上不同空间位置的分布特性,从而获得散斑的线性传输性质.

由于散斑的分布是随机的,在数学上对应一个二维随机函数.从统计光学的角度来看,可以依据CPP面型的统计性质推导出靶面光场的统计性质.把CPP元件面型看作一个空间相关长度很短的随机函数,则靶面光场就是散斑光场,这是位相随机叠加的结果,满足复高斯分布.其分布的概率密度函数为[16]

其中σ是随机函数的方差;EReal是光场复振幅的实部;EImag是光场复振幅的虚部.

散斑高阶统计特性,可以用自相关函数来进行描述.先从一个极端条件出发,即假设CPP面型的相关长度为0,也就是在相关函数为δ函数的情况下,散斑在深度方向上的自相关函数Γ(∆z)为[18]

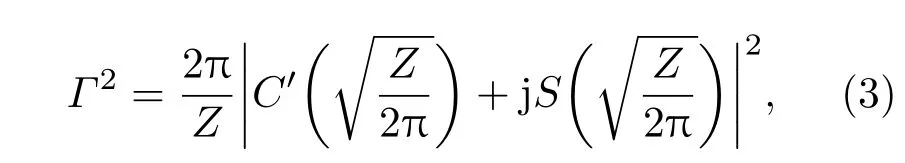
当z/d=4/0.4=10时,∆z=480λ,即深度方向的相关长度为480λ. 常见的物理实验中取λ=351 nm时,可得相关长度约为169µm,这就是利用统计理论对散斑深度方向相关长度的一个预估.

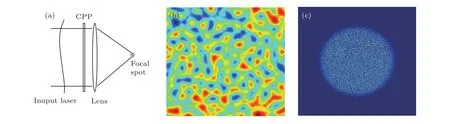
图1 CPP光路原理和散斑光场的整体形态 (a)CPP光路原理;(b)CPP元件面型分布;(c)CPP的远场光强和散斑分布Fig.1.Light path of CPP and the speckle fi eld:(a)Principle scheme of CPP;(b)surface shape of CPP;(c)far fi eld distribution and speckle of CPP.

相关函数表示光场各点之间的关联性,靶面光场的相关长度通常为一个固定小值.有限的相关性对非线性作用的相位匹配过程起到了破坏作用,从而降低了各种非线性效应,这是激光驱动核聚变的一个重要机制[19,20].

现在回到Collins衍射积分.当光由真空传输进入到等离子体中时,由于等离子体折射率小于1,其传输特性会发生变化.在具体计算过程中首先需要推导出傍轴条件下的ABCD传输矩阵,当传输矩阵的A,D元素等于1时,Collins积分退化为菲涅耳衍射积分.

首先分析无等离子体情况下,离焦量为∆时,也就是观察面到透镜距离为f+∆时,传输矩阵为

将其代入Collins公式,并考虑到离焦量远小于焦距,可将计算过程表示为

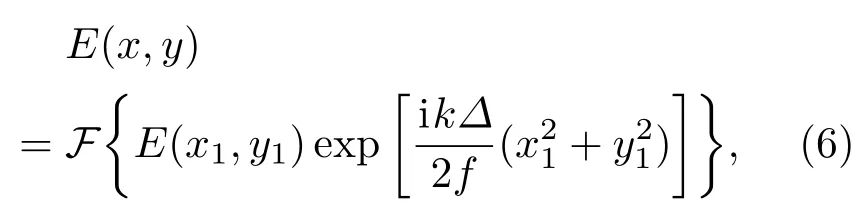
其中F{·}表示傅里叶变换.在计算中取空气(真空)介质的折射率等于1.

考虑等离子体中的线性光传输和电磁波的逆轫致吸收过程时,等离子体的等效介电常数为

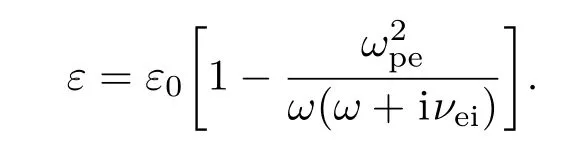
其中νei是电子-离子碰撞率;ε0是真空介电常数;ω是激光频率;ωpe是等离子体频率;e是电子电荷.经过逆轫致吸收后,场强将呈指数衰减.强度的减小对光场分布不会造成明显影响,为了使分析过程更为清晰,忽略吸收项,则等离子体的等效介电常数简化为.由此可推导出等离子体的等效折射率n为

其中ne是电子密度;me是电子质量.本文主要研究光的线性传输,因此实际使用的等离子参数只有等效折射率n.通常等离子体折射率具有一个分布函数,下面将使用一些合理的假设来估计这个折射率分布函数,并据此推导ABCD传输矩阵.

ICF打靶过程中,在高功率激光作用下,靶物质处于喷发状态,则靶外存在一定分布的等离子体.等离子体的密度从外到内有一个渐变的过程,在光传输方向上密度逐渐增大,同时温度也逐渐增高,如图2所示.此时折射率也有相应的变化,即折射率只是坐标z的函数,且向内逐渐变小.这种情况下可以先对等离子体进行分层,然后逐一计算ABCD矩阵再求积,从而得到密度渐变等离子体的ABCD矩阵:

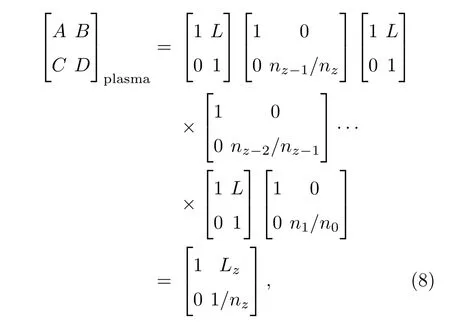
其中nz为等离子体的折射率,其为坐标z的函数;是光程的函数.

可以设定等离子体刚好位于焦面之后,合成的传输矩阵等于等离子体的ABCD矩阵乘以透镜到焦面的ABCD矩阵,从而可得

图2 密度渐变的等离子体Fig.2.Plasma with gradual density.

将推导得到的ABCD矩阵代入Collins公式,即可求得激光在等离子体中的线性传输特性.

3 散斑光场的特性变化

利用上述分析模型计算散斑光场的传输变化特性.首先计算散斑在空气中的传输,结果如图3所示.

从图3中可以看出散斑在焦面附近的强度分布是有变化的,随离焦量的增大,散斑分布变化也更明显.比较图图3(a)和图3(c),当离焦量增加到200µm时,散斑分布发生了有较明显的改变,说明此时对应的离焦量应当接近散斑在深度方向的相关长度.还可以根据这种变化进一步计算深度方向的自相关函数,如图4所示.结果表明,数值计算的自相关函数,与理论分析的(4)式相近.这也表明该散斑光场满足统计各态历经特性.

图3 空气中不同离焦量下量的散斑分布,采用局部放大显示 (a)离焦量为0;(b)离焦量为100µm;(c)离焦量为200µmFig.3.Distribution of the speckles with dif f erent defocusing amount in air:(a)Defocusing amount is 0;(b)defocusing amount is 100µm;(c)defocusing amount is 200µm.

从图4中可以看出,散斑光场自相关函数的半极值宽度大约为200µm,与利用(4)式计算得到的结果169µm接近,符合统计光学的预估结果.

接下来,计算散斑光场在等离子体中的传输特性.由于等离子体相对空气而言是光疏介质,因此对散斑构成了畸变.针对图2所示的渐变折射率的等离子体,假设n(z)是线性函数,且有n(0)=1,n(200µm)=0.2,则可将折射率变化写为在得到折射率函数后,可得散斑光场在等离子体中传输的光程:将该参数代入等离子体的ABCD矩阵,并取完全相同的入射散斑光场进行计算.当离焦量为0时,激光场还未进入等离子体中,因此图5(a)与图3(a)完全一致,增加离焦量后计算结果如图5所示.

图4 各态历经的假设下散斑光场的统计自相关函数Fig.4.Autocorrelation function of the speckle field with the ergodic supposition.

从变化规律来看,散斑光场在等离子体中的传输特性与在空气中是相似的,不过当离焦量为100µm时,散斑的分布与空气中离焦量为200µm时已相当接近,这说明等离子体中随着离焦量的增大,散斑光场的变化会更快,散斑光场的相关长度更短.根据具体的计算,散斑光场在等离子体中200µm处的离焦量相当于空气中402.4µm离焦处的焦斑.等离子体密度越大,散斑光场的变化就会越快,自相关长度就越短,这对抑制非线性很有利.

为了更直观地表示出深度方向上的散斑光场传输特性,选择光轴附近的一条直线(x2,y2,f+∆)来计算该方向上的光场,结果如图6所示.

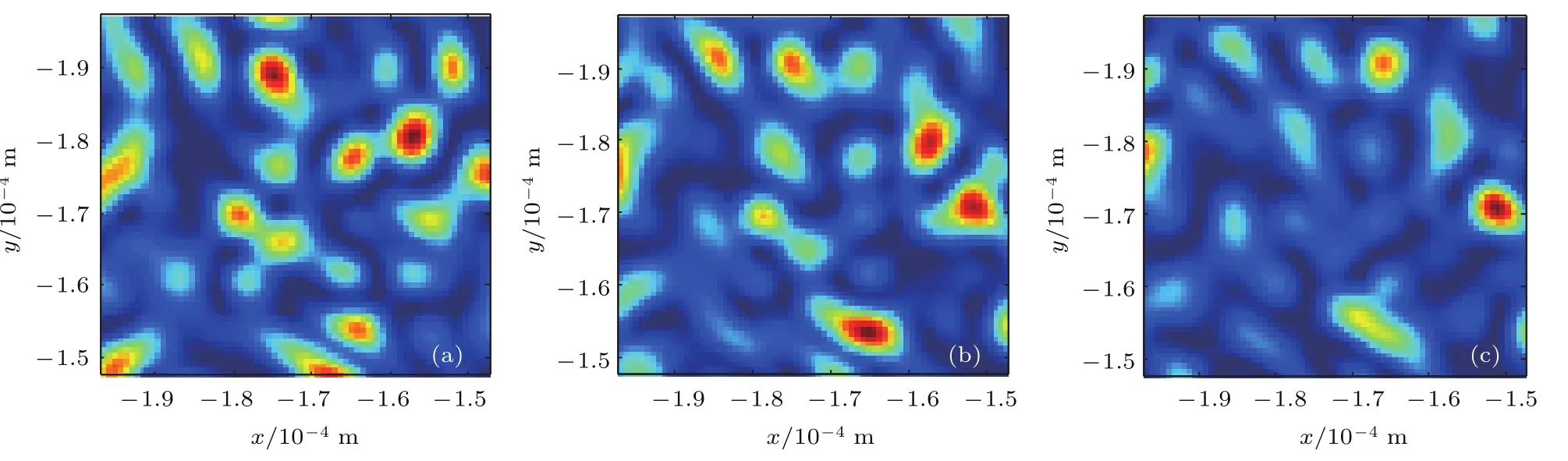
图5 等离子体中不同离焦量下量的散斑分布,采用局部放大显示 (a)离焦量为0;(b)离焦量为100µm;(c)离焦量为200µmFig.5.Distribution of the speckles with dif f erent defocusing amount in plasma:(a)Defocusing amount is 0;(b)defocusing amount is 100µm;(c)defocusing amount is 200µm.

图6 光轴附近深度方向上的稳态散斑光场Fig.6.Steady speckle field in the depth direction near the optical axis.

图6 中∆<0的部分表示在空气(真空)介质中的散斑光场振幅,可看出光场自相关长度约为200µm;∆>0的部分表示在等离子体中的散斑光场振幅,相比空气介质,光场的自相关长度有变小的趋势,斜率变得越来越大,自相关长度已小于100µm.由于等离子体折射率是渐变的,因此自相关长度也是渐变的.根据(7)式可知,随着等离子体密度的增加,其折射率在大约250µm处就不是实数了,光传输截止,因此停止了计算.

深度方向上有限的相关长度是散斑光场最重要的参数,可以认为,只有在相关长度内才能满足位相匹配和非线性积累.在该长度之外,对非线性作用的相位匹配过程起到了破坏作用,因此散斑能明显降低各种非线性效应.另外,根据(4)式,如果z/d减小一半,就可以将散斑相关长度∆z减小到原来的1/4,这将对非线性作用起到更好的抑制效果.美国国家点火装置采用了较短焦距的打靶透镜,应该就是源于这一效应.另外,从图5和图6的结果可知,散斑光场对小折射率等离子体,也就是靠近临界密度等离子体的非线性抑制效果更好,这个结论可以作为物理实验的参考.

4 结 论

为了分析ICF打靶过程中散斑与等离子体的相互作用,建立了散斑光场在等离子体中传输中的分析模型,并对散斑光场在等离子体中的线性传输特性进行了定量计算.计算结果表明,由于散斑光场是个伪随机光场,相当于在传播方向上引入了随机位相,因此在等离子体中传输后,激光散斑的相干性会快速减弱,从而抑制多种等离子体非线性作用的出现.如果以光场的相关长度作为标准,散斑光场对大折射率等离子体,即低密度等离子体的非线性抑制效果较差,对高密度离子体的非线性抑制效果较好.

另外,即使采用了CPP和散斑光场照明,仍然有多种非线性效应产生,不能彻底消除反常吸收.对于这些非线性现象,需要精确地模拟和预测.利用本文提出的散斑光场分析模型,可以很好地了解实际光场在等离子体中的分布和变化,这将是诊断等离子体参数、研究非线性效应的基础,也是进一步抑制各类非线性效应的前提.

[1]Myatt J F,Zhang J,Short R W,Maximov A V,Seka W,Froula D H,Edgell D H,Michel D T,Igumenshchev I V,Hinkel D E,Michel P,Moody J D 2014Phys.Plasmas21 055501

[2]Leeper R J 2011Plasma and Fusion Research6 1104012

[3]Kurilenkov Y K,Tarakanov V P,Kov S U G 2010Plasma Phys.Rep.36 1227

[4]Chang T Q 1991Laser-plasma Interaction and the Laser Fusion(Changsha:Hunan Science Press)p2(in Chinese)[常铁强 1991激光等离子体相互作用与激光聚变(长沙:湖南科学技术出版)第2页]

[5]Mei Q Y,Zhao X W,Li W H,Jiang X H,Xie P,Zheng Z J,Tang D Y 1994High Power Laser and Particle Beams54 186(in Chinese)[梅启庸,赵雪薇,李文洪,蒋小华,谢平,郑志坚,唐道源1994强激光与粒子束54 186]

[6]Montgomery D S 2016Phys.Plasmas23 055601

[7]Livesscu D,Wei T,Mark R P 2011J.Phys.318 082007

[8]Dubinov A E,Petrik A G,Kurkin S A,Frolov N S,Koronovskii A A 2016Phys.Plasmas23 042105

[9]Xiang J,Zheng C Y,Liu Z J 2010Acta Phys.Sin.59 8717(in Chinese)[项江,郑春阳,刘占军 2010物理学报59 8717]

[10]Zhang L,Dong Q L,Zhang J,Wang S J,Sheng Z M,He M Q,Zhang J 2009Acta Phys.Sin.58 1833(in Chinese)[张蕾,董全力,赵静,王首钧,盛政明,何民卿,张杰2009物理学报58 1833]

[11]Hafizi B,Palastro J P,Gordon D F,Jones T G,Helle M H 2015Opt.Lett.40 1556

[12]Zhou Y L,Sui Z,D I Y C,Xu L X,Ming H 2014Chin.Opt.Lett.12 92

[13]Rawat P,Gauniyal R,Purohit G 2014Phys.Plasmas21 011101

[14]Brunel F 1988Phys.Fluids31 2714

[15]Estabrook K G,Valeo E J,Kruer W L 1975Phys.Fluids18 1151

[16]Goodman J W(translated by Cao Q Z,Chen J B)2007Speckle Phenomena in Optics:Theory and Applications(Beijing:Science Press)p1(in Chinese)[约瑟夫·古德曼 著(曹其智,陈家璧 译)2007光学中的散斑现象理论与应用(北京:科学出版社)第1页]

[17]Lü B D 1991Laser Optics(Chengdu:Sichuan University Press)p16(in Chinese)[吕百达 1991激光光学(成都:四川大学出版社)第16页]

[18]Goodman J W(translated by Cao Q Z,Chen J B)2007Speckle Phenomena in Optics:Theory and Application(Beijing:Science Press)p71(in Chinese)[约瑟夫·古德曼著 (曹其智,陈家璧 译)2007光学中的散斑现象理论与应用(北京:科学出版社)第71页]

[19]Tikhonchuk V T,Mounaix P,Pesme D 1997Phys.Plasmas4 2658

[20]Glenzer S H,Arnold P,Bardsley G,Berger R L,Bonanno G,Borger T,Bower D E,Bowers M,Bryant R,Buckman S,Burkhart S C,Campbell K,Chrisp M P,Cohen B I,Constantin C 2004Inertial Fusion Sciences and Applications2003 207