一种自适应分数阶偏微分图像增强模型*

2018-05-08李伟凯王政霞

计算机工程与科学 2018年4期

李伟凯,王政霞,蒋伟

(1.重庆交通大学信息科学与工程学院，重庆 400074;重庆交通大学数学与统计学院，重庆 400074)

1 引言

图像增强[1,2]是对原始图像进行处理加工，改善图像的显示效果，使其转换成更适合图像分析处理的一类有效方法。本文着重研究基于微分的图像增强方法。传统的基于微分的图像增强方法，如Robert算子[3]、Laplacian算子[4]等在图像增强方面有着广泛的应用。20世纪初期，有学者对整数阶微分图像增强方法[3 - 6]进行改进，通过将其进行加权[6]或结合其他增强方法[3 - 5]的方式，有效提升了整数阶微分的增强效果。但是，这些方法仍无法有效改善整数阶微分对噪声敏感及其容易抑制图像纹理细节的缺点。分数阶微分第一次见于Leibniz与L' Hospital的往来信件[7]，由于分数阶微分具有良好的弱导数性质，并且在数字信号处理中有很好的应用，因此分数阶微分很快引入到图像处理[8]领域。分数阶微分能够在有效提升边缘和纹理细节的同时很好地保留平滑区域的纹理细节[9 - 11]，也有效地解决了整数阶微分对噪声敏感的问题[12,13]。已有学者对分数阶微分进行了改进，如陈昌龙等人[14]通过对图像特征分块，构建分数阶微分掩膜算子，应用到大地图像的图像增强；牛为华等人[15]结合方向导数和分数阶微分，对分数阶微分增强方法进行了改进。蒋伟等人[16]对分数阶微分和整数阶微分进行结合，提出了一种基于有理数阶的偏微分方程图像增强方法，这些方法均具有良好的图像增强效果。

固定阶数的分数阶微分图像增强算子对纹理区域的图像增强有很好的效果，克服了噪声敏感和抑制纹理细节的缺点。虽然微分阶数具有很高的灵活性，但是需要通过不断地调整微分阶数来达到满意的图像增强效果，因此不满足实时图像增强处理需求，且图像不同区域特征是不同的，简单地对一幅图像采用相同的微分阶数是欠妥当的。因此，很多学者开始研究自适应分数阶微分图像的增强方法：如汪成亮等人[17]利用梯度特征建立了一个线性不连续的自适应分数阶微分图像增强模型，取得了良好的图像增强效果；张玉等人[18]在此基础上进行改进，结合图像梯度、信息熵、对比度等因素，利用和声搜索算法选取最优参数，建立了自适应选取分数阶微分阶数的函数；李博等人[19]通过一种基于小概率策略的自适应分数阶微分图像去噪算法，能够在对噪声点进行处理的同时，采用自适应分数阶微分对图像的纹理区域进行增强。目前针对分数阶偏微分图像增强的研究多基于梯度和信息熵等因素，并没有考虑视觉因素的影响，因此对于暗区的图像增强效果不好。

为解决现有自适应分数阶微分图像增强方法对暗区纹理细节增强的不足，本文提出了一种自适应偏微分方程图像的增强算法，主要以亮度(本文中以灰度值进行表示)和梯度作为图像特征进行微分阶数的选取，并通过滑动窗的方式对图像进行增强处理。实验表明，本文方法较传统分数阶微分图像增强算法的增强效果而言，边缘更加明显且纹理突出，对图像的纹理细节显著提升，且清晰度有很大提高，达到自适应图像增强的效果，同时能够满足实时性处理的要求，具有一定的应用前景。

2 预备知识

本文采用G-L分数阶微分定义[12]，G-L分数阶微分的表达式如下：

(1)

其中，G表示G-L，h为微分步长,[ ]为取整符号，a,t分别表示分数阶微分的上下限，Γ(n)=(n-1)!，v表示微分阶数，一维信号f(x)的持续周期x∈[a,t]，考虑到数字图像相邻两个像素的距离为1，因此认定微分步长为1，从而有：

(2)

据此可近似得到一元信号的分数阶微分差分表达式：

(3)

为计算简便，选取像素点四个方向的分数阶微分的前两项系数进行运算：

fx+(x,y)=f(x,y)-v×f(x+1,y)

(4)

fx-(x,y)=f(x,y)-v×f(x-1,y)

(5)

fy+(x,y)=f(x,y)-v×f(x,y+1)

(6)

fy-(x,y)=f(x,y)-v×f(x,y-1)

(7)

通过式(4)～式(7)得到分数阶微分图像增强表达式为：

fE(x,y)=f(x,y)+fx+(x,y)+

fx-(x,y)+fy+(x,y)+fy-(x,y)

(8)

fE(x,y)=5×f(x,y)-v×(f(x-1,y)+

f(x+1,y)+f(x,y-1)+f(x,y+1))

(9)

将卷积运算的相应规则与式(9)相结合，可以得到分数阶偏微分方程微分图像增强的掩模如下：

(10)

3 自适应分数阶偏微分图像增强模型

为构建自适应分数阶偏微分图像增强模型，首先分析信号中微分幅频特性曲线，继而延拓到分析微分阶数与图像灰度值变化幅度之间的关系，微分幅频特性曲线如图1所示。

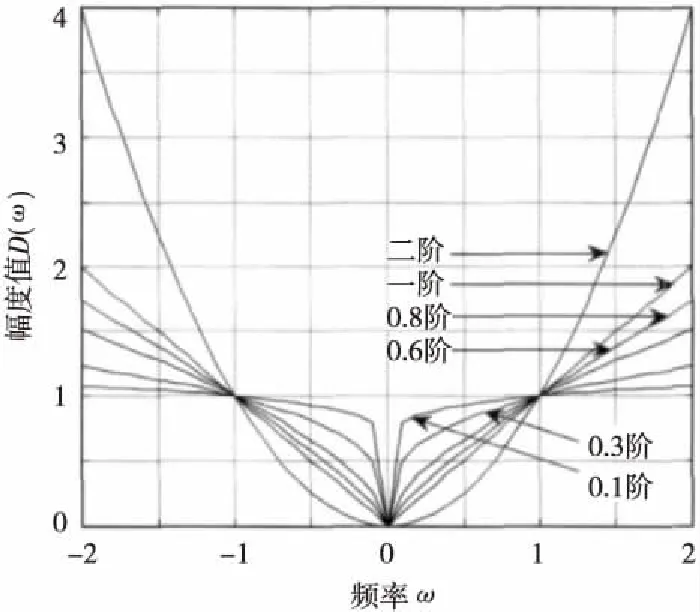
Figure 1 Amplitude frequency characteristics curve of the differential in signal processing图1 信号处理中微分的幅频特性曲线

由图1可以看出，微分阶数越小，对于中低频部分保留得程度越高，但是对于高频部分增强不明显；微分阶数越高，对于高频部分有很好的提升效果，但是对于低频部分会产生抑制作用。图像梯度是反映图像空间变换率[20]的主要特征。图像边缘处，灰度变化剧烈，梯度值相对较大，对应高频部分；图像平滑区域，灰度值稳定，梯度值相对较小，趋近于0，对应低频部分；图像纹理区域，灰度值变化相对平缓，梯度值在适中水平，对应于中高频部分。

然后对图像进行分析，可以得到图像f(x,y)梯度G(Gradient)在其像素点(x,y)上为二维列向量：

(11)

由此，我们可以得到梯度的模值为：

mag(G[f(x,y)])=

(12)

为了简化计算，通过式(12)近似得到梯度模值：

mag(G[f(x,y)])=

(13)

将偏微分∂f/∂x和∂f/∂y近似用差分Δxf(x,y)和Δyf(x,y)来代替，则沿x和y方向的一阶差分表示为：

(14)

将式(13)和式(14)结合，可得梯度的模值为：

mag(G[f(x,y)])=

max(|f(x+1,y)-f(x,y)|,

|f(x,y+1)-f(x,y)|)

(15)

根据人眼对光敏感的关系[21]：

(16)

其中,PMAX表示图像中最大的灰度值;p表示某一像素点的灰度值;k是敏感系数，亚洲人眼大概为1.8，欧洲人眼为2.2，这里取平均值为2。因此,上式可以近似为：

P≈p2/PMAX

(17)

由式(17)可以发现，随着图像灰度阶数的增大，人眼对图像的敏感度也将加强。也就是说，在灰度值小的地方需要对图像进行增强。即微分算子应当随着光强的增加而增加。

在这里，本文提出了一个自适应图像增强算法，对于像素值p和梯度值t，t=mag(G[f(x,y)])，通过构建自适应分数阶微分阶数选取模型v(p,t)，自适应为每个像素点选出最佳微分阶数v。传统观点[17]认为微分阶数的选取与图像梯度的关系呈简单的线性关系，本文认为分数阶微分阶数的增长会受到如避免锐化过度、图片过亮等因素影响的阻碍，考虑到这些关系具有相关性，我们将其视为微分阶数的自增长阻碍。又由于人眼对于梯度和亮度的敏感性不同，我们需要将其映射到人眼的敏感度中去，也就是要除一个人眼的敏感度调节系数u。通过分析文献[17 - 19]，我们发现利用小的微分阶数去处理纹理区域具有好的增强效果，微分阶数与梯度值呈现正比关系。因此，受到logistic模型启发。本文考虑将微分阶数的增长作为一种自阻碍因素进行建模，微分阶数和梯度值与灰度值之间的函数关系可以表述为：

(18)

(19)

式(18)和式(19)中的v表示分数阶数，u1,u2分别表示对亮度和梯度的敏感度调节系数，r1，r2分别表示亮度和梯度微分阶数选取的影响程度，c1,c2分别表示分数阶数对亮度和梯度的自阻碍能力的大小。

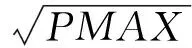
(20)

(21)

考虑到平坦区域和暗区应当选取较小的微分阶数，也就是梯度值和灰度值趋于零时，所选取的微分阶数应当趋于零。同理在边缘区域和亮区应当选取较大的微分阶数。由于微分阶数的选取和以上两个因素是正相关，所以在梯度最大处和亮度最大处时选取的微分阶数应该为1，代入(0,0)(1,1)对式(20)和式(21)求解微分方程得c1=c2=r1=r2=1，即:

(22)

(23)

为保证适当增强，我们选取最大值作为处理的微分阶数：

v=max(v1,v2)

(24)

综上，经过自适应偏微分方程处理的像素点f(x,y)对应的新像素值fE(x,y)为：

fE(x,y)=5×f(x,y)-v(x,y)×[f(x+1,y)+

f(x-1,y)+f(x,y+1)+f(x,y-1)]

(25)

本文的自适应偏微分方程图像增强算法流程如下：

(1)输入原始图像，用矩阵A存储原图像灰度值；

(2)初始化一个矩阵B存储图像各点的梯度值，初始化一个矩阵C作为增强后的图像；

(3)根据式(25)对矩阵A进行处理，依次求出每个像素点对应处理的微分阶数，将得到的梯度存储在矩阵B中；

(4)对图像像素点通过滑动窗的方式，依次按照选择的微分阶数代入掩模进行卷积处理，用矩阵C保存增强后图像；

(5)输出增强后的图像。

本文算法需要计算四个方向的梯度，并且对每个点进行卷积运算，因此对于一幅有N个像素点的图像，本算法所需要的时间频度为T(5N)，时间复杂度为O(N)。本算法需要存储图像各点的像素值、梯度值以及增强后图像的像素值，需要的空间复杂度为S(3N)。本文算法可以在有效的时间和空间复杂度内完成，因此可以应用于实际应用，可以满足一些对实时性要求较高的图像增强任务，具有一定的应用前景。

4 实验效果及分析

考虑到文献[17 - 19]的不同仅仅在于纹理区域的差异，并没有考虑暗区纹理细节问题，而本文主要对暗区的纹理细节增强进行改进。在这里，我们采用以上三篇文献中最经典方法(简称文献方法)[17]、固定微分阶数的图像增强方法以及本文方法对三幅图像分别进行图像增强。我们选取效果最好的v=0.8的分数阶微分的图像增强方法进行图像增强，并进行比较，来验证本文方法的增强效果。本文算法实验运行环境为：CPU为AMD A0PRO-78，实验运行软件为Matlab 2013b，实验效果见图2～图4，图像客观评价结果见表1和表2，运行时间见表3。

实验1对图像Snow进行增强。为方便运算，将原RGB图像转换为灰度图像。从图2可以看出，在亮区部分如上半部分的台阶以及右侧的墙壁，图2b本文方法与图2c文献方法对于纹理细节和边缘均具有良好的图像增强效果，对于暗区部分的增强,如位于下半部分台阶阴影处,本文方法的增强效果明显好于文献方法。图2d固定阶分数阶微分对纹理细节有较好的保留与增强作用，但是使得亮区的图像过亮，影响视觉效果。通过比较直方图可以看出，在0～50这个灰度区间，图2g文献方法大部分灰度值均处于0～25，而图2f本文方法更加均匀且大部分落于25～50，亮区两种方法的效果基本一致。因此，本文对暗区的纹理细节增强效果更好。

实验2选用Matlab自带图像Tire进行图像增强。从图3中可以看到，对于轮胎和轮毂的轮廓以及轮毂与轮胎处等亮区的纹理以及边缘区域，图3b本文方法与图3c文献方法均有良好的增强效果，而对于阴影处的沙砾以及左上角的轮胎细节等暗区的纹理区域，本文方法较文献方法有更好的增强效果。图3d固定阶分数阶微分图像增强方法同样存在失真问题。通过分析灰度直方图可以看出，图3f本文方法在暗区的灰度分布更加均匀，因此在暗区的对比度较文献方法更高，具有更好的视觉效果。因此，本文方法是对暗区图像纹理区域增强的有效方法。

实验3对Girl图像进行图像增强。从图4可以看到在女孩的头发、脸部细节等纹理区域，图4b

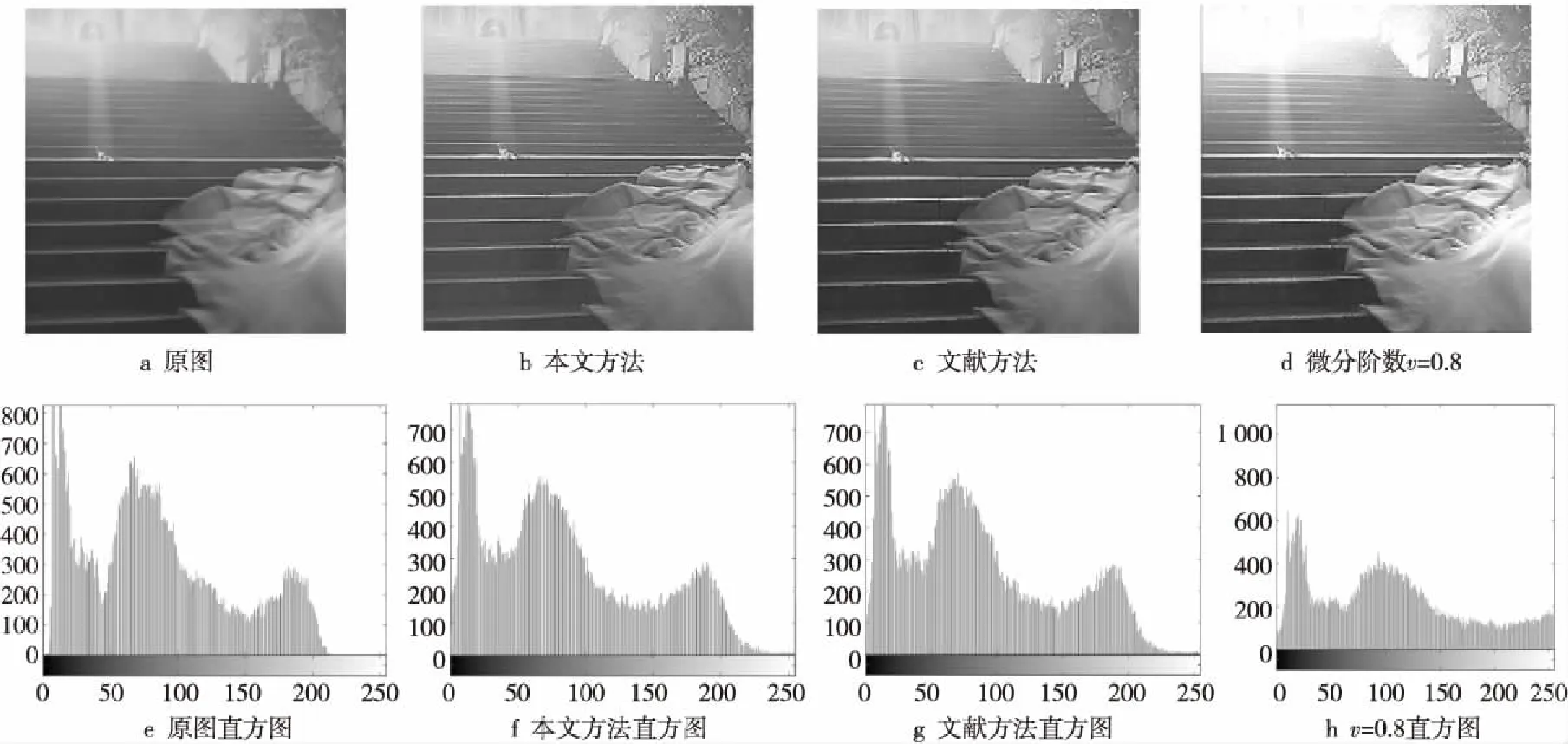
Figure 2 Image enhancement of image Snow图2 对图像Snow的图像增强

本文方法与图4c文献方法均有良好的增强效果，头发的增强效果均很明显，而对于暗区衣服褶皱处的纹理细节，本文方法较文献方法有更好的增强效果。图4h固定阶分数阶微分图像增强方法依然会产生色彩上的一些失真。通过分析灰度直方图可以看出，图4f本文方法在暗区的灰度分布更加均匀，灰度在亮区上的分布情况与文献方法基本一致，因此在暗区的对比度较文献方法更高，具有更好的视觉效果，因此本文方法是对暗区图像纹理区域增强的有效方法。

通过三组实验可以发现，文献方法有效地增强了亮区的纹理细节，并且对于边缘区有很好的增强效果。微分阶数随像素点梯度值的变化而灵活变化，较现有固定阶数的图像增强方法有了很大的进步，但是暗区的纹理细节仍没有被很好地增强。灰度直方图在暗区的分布与原图接近，因此暗区图像增强效果较差，这是因为文献方法并没有考虑像素亮度的因素，从而导致暗区增强不足。经过文献方法增强的亮区纹理效果显得并不平滑，这是因为文献方法中，纹理区域边缘区域的划分有明显的界限，导致纹理区域与边缘区域分界点的梯度相差很小，但处理的微分阶数可能差距较大。相较之下，本文模型对于微分阶数的选取是连续的，对于纹理和边界的定义是模糊的，见式(22)，同时本文模型对亮区边缘的纹理细节增强的同时，也对暗区的纹理细节进行了更好的增强，因此细节处理更好，较文献方法有了一定的改进。

上文通过主观视觉效果来对本文方法的图像增强效果进行主观评价。为了更好地验证新模型的有效性，本文从客观指标上来评价其图像增强效果。考虑到本文主要工作为图像锐化，也就是增强图像的对比度，在数字图像上反应为图像的梯度增加和灰度分布的改变。因此，在本文中，我们使用平均梯度和信息熵作为图像增强的客观评价指标。平均梯度越大，图像的对比度越高，相对应的图像增强的效果也就越好，同时，信息熵越高，图像的对比度也就越高。我们分别以图像Tire、图像Snow、图像Girl为例，对本文方法进行客观评价，并与文献方法进行比较，从而对本方法进行客观的分析和评判。

平均梯度AG(Average Gradient)计算公式如下：

(26)

其中，G为图像梯度矩阵，m,n为图像尺寸。

信息熵IE(Information Entropy)的计算公式如下：

(27)

其中，pi表示灰度值i在图像中出现的概率。

通过式(26)计算所得的不同方法对三幅图像增强所得到的图像的平均梯度结果见表1。

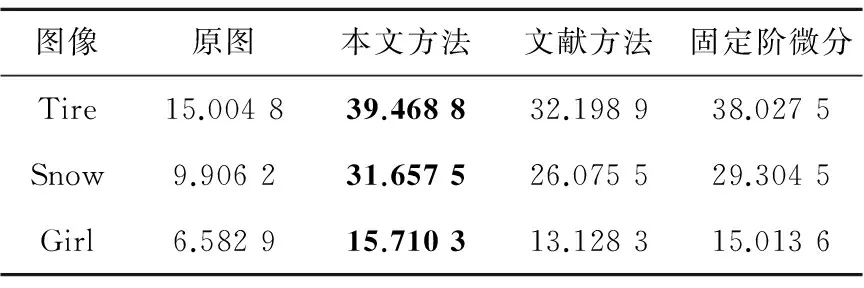
Table 1 Average gradient of differentimages after image enhancement表1 对不同图像增强处理的平均梯度

通过式(27)计算所得的不同方法对三幅图像增强所得到的图像的信息熵结果见表2。

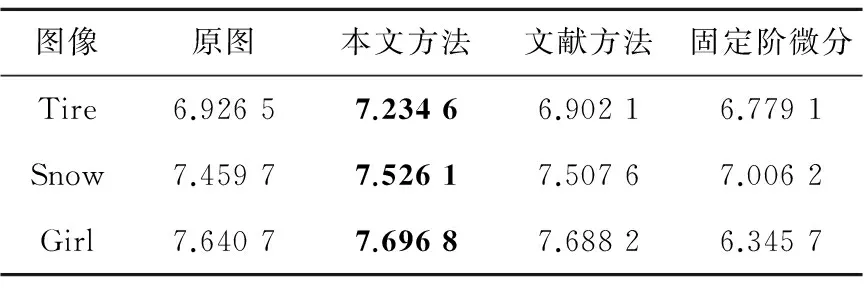
Table 2 Information entropy of differentimages after image enhancement表2 对不同图像增强处理的信息熵

不同实验方法对于图像处理时间如表3所示。

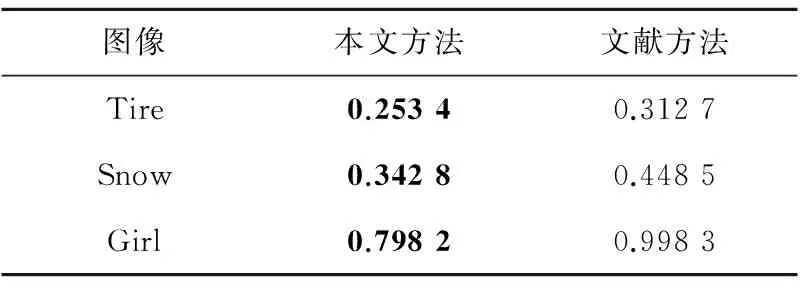
Table 3 Processing time of imageenhancement for different images表3 对不同图像增强处理的运行处理时间 s

从表1和表2可知，对于图像的增强效果，本文方法增强后较文献方法具有一定的进步，原因是，在暗区纹理细节处，本文方法能够比文献方法选取更小的微分阶数，因此能够得到更好的增强效果。对比实验说明本文方法是一个行之有效的方法，并且通过表3可以看出，本文方法能够有效地满足实时性的图像处理需求。

5 结束语

本文以现有偏微分方程图像增强理论和已有的自适应性分数阶微分图像增强模型为基础,结合人眼对于亮度的敏感性，提出了一种基于模糊域的梯度和像素点亮度的自适应偏微分方程图像增强新模型。通过本文建立的模型自适应地选取微分阶数来进行图像处理，进而对图像各个像素点进行动态的增强处理，从而得到较好的图像增强效果。在与固定阶分数阶微分和传统图像增强方法还有现有文献的方法进行的比较中，可以发现本文方法较之前方法有了一定的提高，暗区的纹理细节显著增强。本文方法可用于沥青路面或夜间监控图像的图像增强工作中，通过实验对比客观评价，本文方法在平均梯度、信息熵方面有很好的提升，同时运算速度有一定的进步。实验结果表明，本文提出的新模型是行之有效的；通过时间复杂度和空间复杂度分析，本方法具有一定的实际应用价值。

参考文献:

[1] Gonzalez R C,Woods R E.Digital image processing[M].Boston:Addison-Wesley Longman Publishing Co,2001.

[2] Sonka M,Hlavac V,Ceng R B D M.Image processing,analysis,and machine vision[M].Belmont:Thomson Learning,2008:685-686.

[3] Zhang Hui,Chen Hong-ming.Hybrid SUSAN algorithm and Robert algorithm for image edge detection filtering technique [J].Computer Science,2013,40(3):302-304.(in Chinese)

[4] Gupta S,Porwal R.Combining Laplacian and Sobel gradient for greater sharpening[J].ICTACT Journal on Image & Video Processing,2016,6(4):1239-1243.

[5] Wu Jie, Chen De-zhi, Guo Cheng-zhi.An enhancing image method based on sobel edge detect arithmetic innovating [J].Laser and Infrared,2008,38(6):612-614.(in Chinese)

[6] Sun Zeng-guo,Han Chong-zhao.Image enhancement based on Laplacian operator [J].Computer Application Research,2007,22(1):222-223.(in Chinese)

[7] Leibniz G W.Correspondatice De Lebniz Avec Hugens,Van Zulichem Et Le Marquis De L' Hospital[M]. Paris:Libr de A,1853:297-302.

[8] Mandelbrot B B.Thr fractal geometry of nature[M].New York:W H Freeman and Company,1983.

[9] Pu Yi-fei,Patrick S,Zhou J L,et al.Fractional partial differential equation denoising models for texture image[J].Science China Information Sciences,2014,57(7):1-19.

[10] Zhang Y, Pu Y, Zhou J.Construction of fractional differential masks based on Riemann-Liouville definition[J].Journal of Computational Information Systems,2010,6(10):3191-3199.

[11] Zhang Yong, Pu Yi-fei,Zhou Ji-liu. Image enhancement based on fractional differentials[J].Computer Application Research,2012,29(8):3195-3197.(in Chinese)

[12] Yang Zhu-zhong,Zhou Ji-liu,Huang Mei,et al.Edge detection based on fractional differentials [J].Journal of Sichuan University(Engineering Science Edition),2008,40(1):152-157.(in Chinese)

[13] Yang Zhu-zhong,Zhou Ji-liu,Yan Xiang-yu,et al.Image enhancement based on fractional differentials [J].Journal of Computer-Aided Design & Computer Graphics,2008,20(3):343-348.(in Chinese)

[14] Chen Chang-long, Sun Ke-hui. Fractional-order differential image enhancement algorithm based on image characteristics division[J].Computer Engineering and Applications,2016,52(14):186-191.(in Chinese)

[15] Niu Wei-hua,Meng Jian-liang,Cui Ke-bin,et al.Image enhancement method using Grümwald-Letnikov fractional directional differential[J].Journal of Computer-Aided Design & Computer Graphics 2016,28(1):129-137.(in Chinese)

[16] Jiang Wei, Li Xiao-long,Liu Ya-wei,Image enhancement new model based on rational-order partial differential [J].Journal of Sichuan University(Natural Science Edition),2016,53(1):47-53.(in Chinese)

[17] Wang Cheng-liang, Lan Li-bin, Zhou Shang-bo.Adaptive fractional differential and its application to image texture enhancement [J].Journal of Chongqing University,2011,34(2):32-37.(in Chinese)

[18] Zhang Yu,Wang Zheng-yong,Teng Qi-zhi,et al.A image enhancement and application based on adaptive fractional-order differential [J].Journal of Sichuan University(Natural Science Edition),2015,52(1):93-100.(in Chinese)

[19] Li Bo, Xie Wei.Image enhancement and denoising algorithms based on adaptive fractional differential and integral [J].Systems Engineering and Electronics,2016,38(1):185-192.(in Chinese)

[20] Zhang S Q,Zhou J Y.Centerline extraction for image segmentation using gradient and direction vector flow active contours[J].Journal of Signal and Information Processing,2013,4(4):407-413.

[21] Kang Mu, Li Yong-liang. An adaptive image enhancement algorithm based on human visual properties [J].Optical Engineering,2009,36(7):71-77.(in Chinese)

附中文参考文献：

[3] 章慧,陈宏明.融合SUSAN算法和Robert算法的图像边缘检测与滤波处理技术[J].计算机科学,2013,40(3)： 302-304.

[5] 吴捷,陈德智,国成志.Sobel边缘检测算法的变异实现图像增强[J].激光与红外,2008,38(6)： 612-614.

[6] 孙增国,韩崇昭.基于Laplacian算子的图像增强[J].计算机应用研究,2007,22(1)： 222-223.

[11] 张涌,蒲亦非,周激流.基于分数阶微分的图像增强模板[J].计算机应用研究,2012,29(8)： 3195-3197.

[12] 杨柱中,周激流,黄梅,等.基于分数阶微分的边缘检测[J].四川大学学报(工程科学版),2008,40(1)：152-157.

[13] 杨柱中,周激流,晏祥玉,等.基于分数阶微分的图像增强[J].计算机辅助设计与图形学学报,2008,20(3)： 343-348.

[14] 陈昌龙,孙克辉.基于图像特征分块的分数阶微分图像增强算法[J].计算机工程与应用,2016,52(14)：186-191.

[15] 牛为华,孟建良,崔克彬,等.利用Grümwald-Letnikov分数阶方向导数的图像增强方法[J].计算机辅助设计与图形学学报,2016,28(1)：129-137.

[16] 蒋伟,李小龙,刘亚威.基于有理数阶偏微分的图像增强新模型[J].四川大学学报(自然科学版),2016,53(1)：47-53.

[17] 汪成亮,兰利彬,周尚波.自适应分数阶微分在图像纹理增强中的应用[J].重庆大学学报,2011,34(2)： 32-37.

[18] 张玉,王正勇,滕奇志,等.自适应分数阶微分的图像增强及应用[J].四川大学学报(自然科学版),2015,52(1)： 93-100.