基于扩展卡尔曼滤波的时钟模型辅助定位算法*

宋建材,候春萍,薛桂香

(1.天津大学电子信息工程学院,天津 300072;2.河北工业大学计算机科学与软件学院,天津 300430; 3.天津商业大学信息工程学院，天津 300134)

1 引言

全球卫星导航系统GNSS(Global Navigation Satellite System)的接收机时钟精度低，无法与星载原子钟同步，卫星与接收机之间的钟差Δt是未知的，至少需要4个观测方程联立才能实现用户三维定位和授时[1]。对于平面运动的车载或船载用户或有高程辅助的终端用户，只需要跟踪接收3颗可见卫星就可实现二维定位算法。如果视野内可见卫星数目小于3颗时，接收机通常由于缺少足够的观测量而无法实现正常定位解算，GNSS系统处于不可用状态[2]。随着我国城镇化的快速发展，在城市峡谷和郊区树林多的道路上很容易对卫星信号有遮挡，引起可见卫星数目不足，使得接收机无法定位的情形愈来愈多，在某些定向干扰场景下，因接收机跟踪的卫星数量减少而不能正常工作。

为提高在信号遮挡或者某些定向干扰场景时GNSS接收机的可用性，目前常用的手段主要有两大类：一是利用惯性导航系统INS(Inertial Navigation System)组合[3,4]实现连续定位，特别是近年随着微电子机械系统MEMS(Micro Electro-Mechanical Systems)技术的发展，GNSS/MEMS组合定位方法逐渐成熟[5,6]，增强了GNSS在信号缺失时的可用性，缺点是需陀螺仪与加速度计辅助传感器，增加了硬件成本；二是从电子地图精确匹配角度实现了辅助定位[7,8]，但这类算法依赖电子地图数据和地图匹配算法的精度，定位误差相对较大，由于与电子地图的路线匹配，因此仅适用于特定运动路线场景。此外，之前的学者还提出了基于灰色理论的钟差模型预测方法[9]，但难以利用递推方法与卡尔曼滤波结合；时钟模型最小二乘法解[10]和钟差系列预测方法[11]的缺点是只利用当前历元测量信息，定位精度较差。针对上述方法的缺点，本文提出了一种基于接收机时钟模型的辅助定位算法，主要思想是同时利用跟踪环路的伪距和多普勒观测量，通过扩展卡尔曼滤波EKF(Extend Kalman Filter)实时估算接收机时钟的钟偏和钟漂，构建时钟数学模型，在导航信号部分缺失情况下采用该时钟模型参数进行辅助定位，可以继续按照原精度级别完成定位解算。仿真分析和车载实验结果表明，该方法可在仅有2～3颗卫星信号可见时，实现高精度二维和三维定位，在硬件不变前提下，提高了系统可用性。

2 接收机时钟模型

在GNSS观测模型中接收机钟差对定位精度有非常大的影响，微小的钟差会导致较大的测距误差和相位测量误差。接收机钟差δt建模为：

δt=δtu+δfu·t(t1≤t≤t2)

其中，δtu：用户接收机时钟偏差；δfu：用户接收机时钟漂移速度；(t1,t2):钟差多项式的有效周期。

提取状态变量：

用状态方程描述为：

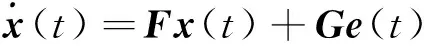
接收机时钟模型可以通过拉氏变换离散化。

其中,L是拉氏变换算子，I是单位矩阵，Ts为测量采样周期，也是状态方程差分步长。接收机时钟的Kalman滤波状态方程可表示为：

xk=Acxk-1+wk-1

其中，wk-1代表噪声e(t)引起的过程噪声向量，噪声向量e(t)所对应的权矩阵为：

其中，St为钟差噪声的自协方差，Sf为频偏噪声的自协方差。

测量噪声方差：

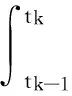
因为该模型中各个相关的矩阵均为常系数阵，所以过程噪声wk的协方差Qk也不随时间变化，其值为：

3 扩展卡尔曼滤波

扩展卡尔曼滤波(EKF)是一种非线性系统滤波方法，可将状态转移方程和测量方程在当前估值处利用泰勒展式进行线性化。一个非线性系统方程可表示为：

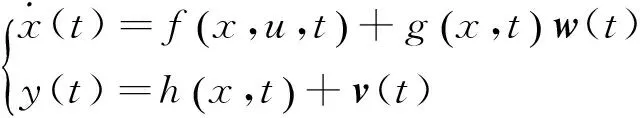
其中：

f表示三者之间的非线性关系(系统状态x、输入量u和时间t)；

h是关于系统状态x和时间t的非线性函数；

w(t)是系统噪声向量；

v(t)是测量噪声。

假设在时刻t系统状态为x(t)，估计值x*(t)，此时系统和测量函数分别为：

估计量偏差为：

δx(t)=x(t)-x*(t)

用泰勒级数展开，略去高阶项，得到:

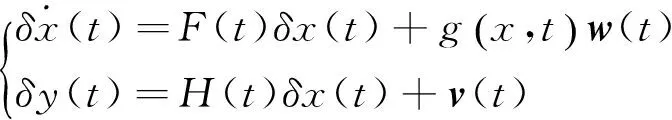
其中：

GNSS的伪距和伪距率观测方程都是非线性的，因此扩展卡尔曼滤波处理位置速度和时间PVT(Position Velocity and Time)解算，可以降低噪声干扰，提高接收机定位精度。

4 接收机时钟辅助定位方程

针对行人、汽车、舰船等低动态载体而言，接收机运行情况可以用8个状态变量来描述，即三个位置分量(x,y,z)、三个速度分量(vx,vy,vz)和接收机时钟的两个变量(δtu,δfu)。其状态变量为:

(x,y,z,vx,vy,vz,δtu,δfu)

常系数的状态转移矩阵为:

状态向量X=[xvx]的协方差矩阵Qx表示为：

其中Svx为X速度分量的噪声功率谱密度。

整个算法的流程如图 1所示。算法首先进行EKF滤波估计变量初始化，然后判断当前的卫星数目，切换到不同的定位算法。采用多次估计平均方法，可以提高时钟模型精度，以此作为接收机时钟参数，固化存储在内置Flash。

Figure 1 Flowchart of colck-model-assisted positioning algotithm图1 时钟辅助定位算法流程图

5 仿真分析与算法验证

该实验利用加拿大NovAtel公司的OEMStar板卡进行数据采集，仿真计算机利用ThinkPad X250、Intel i5-5300处理器、8 GB内存，操作系统是64位Windows 7，仿真软件版本是Matlab 2010a。

为了测试接收机跟踪不同可见卫星数量时，算法自适应切换功能和定位性能，利用OEMstar提供的ASSIGN和UNASSIGN命令指定信道跟踪特定卫星，从而把接收卫星信号数量限定在指定个数，模拟接收机分别跟踪大于4颗、4颗、3颗、2颗四种卫星数量的定位场景。接收机状态分别有静态放置、车载运动两种。

接收机必须先跟踪4颗以上卫星信号，以便扩展卡尔曼滤波器能够精确估计出接收机时钟偏差和漂移速度参数，得到其数学模型。1分钟后通过设置命令减少接收机跟踪的卫星数量至3颗卫星，系统处于信号缺失的不完整星座状态，最小二乘法无法三维定位，但通过EKF估计仍能定位，接收机的时钟偏差和漂移速度曲线如图2所示。

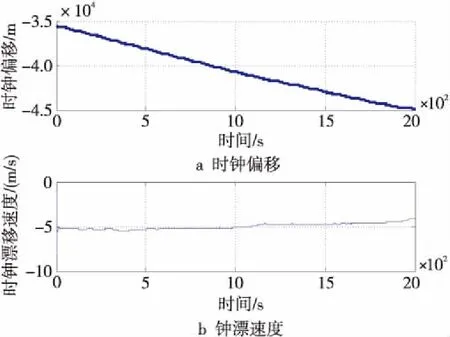
Figure 2 Receiver clock bias and drift speed curve图2 接收机钟偏和钟漂速度曲线

当接收机静止状态时，EKF定位误差如图3所示，包括东向、北向、垂向误差三个分量。由图3可知，在信号缺失状态下，接收机定位结果精度稳定，大约在1 000 s以内定位误差并没有出现明显增大，在1 200 s以后北向误差逐步增大发散，大约在1 500 s时北向误差增大到50 m左右，而东向和垂向误差变化不明显；EKF测速误差如图4所示，可见信号缺失时卡尔曼滤波的测速误差仍非常小。

Figure 3 3D position error curve based on EKF during signal outage图3 信号缺失EKF三维定位误差曲线

Figure 4 Error curve of 3D velocity measurement during signal outage图4 信号缺失时EKF三维测速误差

当接收机处于车载运动状态时，定位结果曲线跟实际工作中的定位曲线对比如图5示，当卫星信号缺失只有3颗可见卫星时，利用扩展卡尔曼滤波器估计接收机时钟参数辅助，继续完成三维定位；当接收机跟踪的卫星信号继续减少至2颗卫星时，基于扩展卡尔曼滤波的时钟辅助算法就只能进行2维定位。定位算法可根据当前的卫星数目自动进行切换。水平定位误差曲线如图6所示，在这种情况下，由于扩展卡尔曼滤波对接收机时钟参数的精确估计，大约在300 s内二维定位误差也没有急剧恶化趋势，在390 s左右系统发生了解算算法的自动切换，系统的误差逐渐增大，北向误差增大到20 m以上，在450 s左右北向误差增大到30 m以上，不满足精密定位的要求，但是对于系统的概略位置估计和系统状态估计仍有一定的帮助。

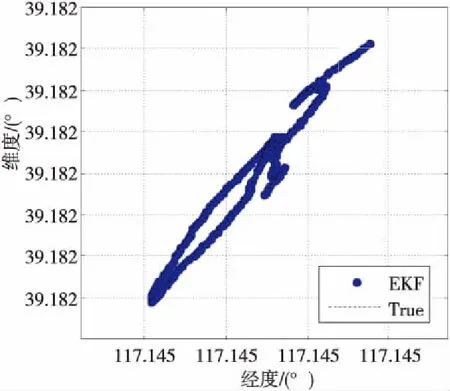
Figure 5 Dynamic position curve based on EKF during signal outage图5 信号缺失时EKF车载动态定位曲线

Figure 6 2D position error curve based on EKF during signal outage图6 信号缺失EKF水平定位误差曲线

6 结束语

本文针对不完整星座提出了一种新的基于EKF的时钟模型辅助定位方法。首先在星座完整时，通过综合利用伪距和多普勒观测量，通过扩展卡尔曼滤波器实时估算得到接收机钟偏和钟漂参数，通过构建接收机时钟数学模型，在导航信号缺失情况下，利用扩展卡尔曼滤波技术根据该时钟模型进行推导辅助定位。通过分别对静态和车载实验分析，结果表明该方法可在卫星导航信号缺失、星座不完整时仍能够在一定时间内以较高精度继续完成实时定位解算，在不增加硬件成本前提下提高了可用性，具有较好的应用价值。

参考文献:

[1] Xie Gang.Principles of GPS and receiver design[M].Beijing:Publishing House of Electronics Industry,2009.(in Chinese)

[2] Elliott K,Christopher H.Understanding GPS:Principles and applications [M].Boston:Artech House,2005.

[3] Miller I,Campbell M.Sensitivity analysis of a tightly-coupled GPS/INS system for autonomous navigation [J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(2):1115-1135.

[4] Jwo D J,Yang C F,Chuang C H,et al.A novel design for the ultra-tightly coupled GPS/INS navigation system[J].Journal of Navigation,2012,65(4):717-747.

[5] Qin Hong-lei,Cong Li,Sun Xing-li.Accuracy improvement of GPS/MEMS-INS integrated navigation system during GPS signal outage for land vehicle navigation [J].Journal of Systems Engineering and Electronics,2012,23(2):256-264.

[6] Angrisano A,Petovello M,Pugliano G.Benefits of combined GPS/GLONASS with low-Cost MEMS IMUs for vehicular urban navigation [J].Sensors,2012,12(4):5134-5158.

[7] Obst M,Bauer S,Reisdorf P,et al.Multipath detection with 3D digital maps for robust multi-constellation GNSS/INS vehicle localization in urban areas[C]∥Proc of 2012 IEEE Intelligent Vehicles Symposium (IV),2012:184-190.

[8] Fouque C,Bonnifait P.Matching raw GPS measurements on a navigable map without computing a global position [J].IEEE Transactions on Intelligent Transportation Systems,2012,13(2):887-898.

[9] Teng Yun-long,Shi Yi-bing,Zheng Zhi.Research on positioning method under GPS incomplete constellation[J].Journal of Astronautics,2011,32(1):93-97.(in Chinese)

[10] Wang Er-shen, Zhang Shu-fang,Hu Qing.Incomplete con-

stellation positioning method for GPS receiver augmented with clock bias model [J].Journal of Dalian Maritime University,2009,35(2):59-61.(in Chinese)

[11] Guo Rong-chang, Jin Wen-jun,Fang Duo-wang,et al.Reseach on positioning method under GPS incomplete constellation[J].Journal of the China Railway Society,2015,37(3):42-45.(in Chinese)

附中文参考文献：

[1] 谢刚.GPS原理与接收机设计[M].北京:电子工业出版社,2009.

[9] 滕云龙,师奕兵,郑植.GPS不完整星座定位方法研究[J].宇航学报,2011,32(1):93-97.

[10] 王尔申,张淑芳,胡青.基于时钟偏差模型的GPS不完整星座定位方法[J].大连海事大学学报,2009,35(2):59-61.

[11] 郭荣昌,靳文军,范多旺,等.GPS不完备条件下定位方法研究[J].铁道学报,2015,37(3):42-45.