野草猴群算法的传感器优化布置方法研究*
2018-05-08杜国璋彭珍瑞
殷 红,杜国璋,彭珍瑞,马 丽
(1.兰州交通大学机电工程学院,甘肃 兰州 730070; 2.兰州交通大学自动化与电气工程学院,甘肃 兰州 730070)
1 引言
传感器优化布置是一种多维优化问题,对其进行高效求解已成为该领域研究的热点问题之一[1]。近年来,逐渐兴起的一些智能算法在解决传感器优化布置问题方面取得了较好的研究成果,如具有不易陷入局部最优、能较好解决组合优化问题中约束条件限制等特点的模拟退火算法、遗传算法、蚁群算法和粒子群算法等。
野草算法IWO(Invasive Weed Optimization)是一种数值型随机优化计算方法,于2006年由伊朗德黑兰大学的Mehrabian和Lucas首次提出[2]。野草在入侵农作物过程中强大的繁殖能力和竞争能力启发了一种寻优的算法思想。算法中引入繁殖进化机制和竞争性生存法则,通过种群初始化-生长繁殖-空间扩散-竞争排斥等迭代步骤,确保了种群的多样性和个体对环境的适应性[3]。
猴群算法MA(Monkey Algorithm)作为另一种仿生学智能优化算法,于2008年由Zhao和Tang首次提出[4]。算法模拟猴群的爬山过程,通过爬-望-跳等步骤不断迭代实现最优解的搜索。猴群算法寻优能力较强,参数设置较少,适合求解复杂函数的优化问题,已在多个领域得到了较好的应用[5,6]。Yi等人[7]在MA的基础上改进提出的简易猴群算法SMA(Simple Monkey Algorithm),较好地实现了传感器的优化布置。
但是,SMA采用随机方式初始化猴群,降低了猴群的多样性和算法的全局搜索能力[8];爬步长的固定,使得猴子可能错失搜寻到局部更优解的机会,求解精度难以提高[9,10];SMA的搜索过程采用随机迭代方式存在搜索方向的盲目性,每一轮迭代产生的最优解相对独立,没有必然的相关性,当前解中的优秀信息不能直接继承到下一轮迭代中,无法对算法的进一步优化产生直接影响。
针对SMA这些有待改进的问题,本文借鉴IWO中野草竞争生长和繁殖的过程,将其应用到SMA猴群后代的进化中,改进为野草猴群算法WMA(Weed Monkey Algorithm)。进化过程猴群的爬步长采用自适应的参数修正技术,目标函数的适应度引入野草的繁殖进化和竞争生存机制,从而提高算法性能。将提出的方法应用于传感器优化布置,取得了较好的效果。
2 野草猴群算法
野草入侵过程复杂,一般需要经历适应环境、繁殖后代、竞争生存等一系列过程。适应度是衡量野草个体生存能力强弱的重要指标。因此,本文将野草繁殖进化和竞争生存机制运用到WMA的猴群中来,以提高猴群的适应能力。
2.1 编码方式及初始化
传统的MA适用于对连续变量的优化问题进行求解,不适宜于整数规划问题。文献[8]对MA的编码方式进行改进,对决策变量进行整数编码,实现了整数规划问题的优化。本文的WMA采用整数编码方式,流程如下:
Step1建立数学模型。对于被测结构而言,传感器布置节点的位置可编号为整数,则可通过有限元模型的建立,进行模态分析,获得整型数据。设候选节点位置为1~m。
Step2种群编码。设种群规模即猴群数量为M。第i种传感器布置方案即第i只猴子xi=[xi1,xi2,…,xin]T,其中i=1,2,…,M,n为传感器的选定数目。编码方式为整数编码。
Step3选取初始种群。种群初始化的方式会影响搜索效果,为了增大初始解的覆盖空间,引入正态分布方法[2],加大解的多样性,降低搜索过程陷入局部最优的可能性。设定每只猴子xi的各个分量xi1,xi2,xi3,…,xin服从数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2),其表达式为:
(1)
在式(1)中,参数μ和σ根据被测结构的实际工况提前预置,合理控制猴群中各猴子xi间的位置分布幅度。
Step4M只猴子表示M种传感器布置方案。每种方案表示从m个候选节点中选取n个作为候选位置布置传感器,每个候选位置由猴子xi中各分量的值表示。
2.2 爬过程
猴子通过爬行迭代到下一个位置,实现在局部空间寻优的过程。设置爬步长因子为a,步长太小会降低迭代效率,步长太大会降低求解精度。为此,采用自适应的变步长na:
(2)
其中,a为初始爬行步长,b为望视野的长度,iter为猴群的当前进化代数,Nmax为最大迭代次数。由式(2)可知,随着爬行次数的增多,爬行步长逐步减小,收缩到a/20。在靠近精确解时,使其小步慢爬,以便更精确地确定最优解[9]。具体步骤如下[10]:
Step1通过式(2)计算本次迭代的爬行步长na。
Step2选取区间[-na,na],在其中产生随机整数Δxij,构成向量Δxi=(Δxi1,Δxi2,…,Δxin)。
Step3得到新位置xi+Δxi,计算f(xi+Δxi),若f(xi+Δxi) Step4重复Step 1~Step 3,直到爬行次数为Nc,结束计算。 望过程是继爬过程之后,在局部空间搜索更优解的过程。猴子在望区间里瞭望新的解,如果新解比当前解更优则替代当前解,否则维持当前解不变。对于第i只猴子,设望视野的长度为b,望过程步骤如下: Step3重复Step 1~Step 2,直到望过程次数为Nw,结束计算。 跳过程是猴子跳出局部空间,实现全局最优搜索的过程。具体步骤如下: 引入野草繁殖思想,每一代向下繁殖的程度取决于猴子个体的适应度值,适应度由式(3)确定: (3) 可行域为xij∈[-100,100],具有最小函数值的猴子具有最高的适应度,可以繁殖后代,产生后代数由式(4)确定[2]: (4) 其中,Ns为猴子后代的数目,向下取整[2]。φ为适应度值,φmax为最大适应度值,φmin为最小适应度值,Smin为后代数的最小值,Smax为后代数的最大值。在具体的应用实例中,参数φmax、φmin、Smax、Smin都是需要提前设置的定值,Ns与φ相当于一次线性函数Ns=Aφ+B,其中A=(Smax-Smin)/(φmax-φmin),B=Smin,因此,式(3)与式(4)之间存在线性关系,如图1所示。 Figure 1 Methods to determine the number of monkey offspring图1 猴子后代数确定方法 由式(3)得到每代适应度最高的猴子产生后代。为了使这些携带优秀特征信息的猴子在猴群中扩大影响范围,对后代进行正态分布初始化。其标准差为[2]: (5) 其中,σiter为第iter次迭代的标准差,itermax为最大迭代次数,σinitial为初始标准差,σfinal为最终标准差,h为非线性调和指数。 将由繁殖进化过程确定的后代群体追加到父代种群中,对所有猴子的适应度进行全体评价,引入竞争排斥机制。适应度高的猴子优先保留到下一代中,筛选时保持猴群规模不变。然后对新猴群循环进行爬、望、跳、繁殖进化、竞争排斥,不断靠近全局最优解。 传感器优化布置问题就是如何用最少数量的传感器在被监测对象上进行最合理的布置,并从中获取最全面的状态信息,为相关工作提供参考依据,是一类典型的组合优化问题[11]。 在传感器优化布置中,传感器布置测点的选择问题是满足一定准则的优化问题[12]。首先确定优化方案数学模型需要满足的准则,即目标函数。待布置传感器结构的各阶模态向量在节点上的值形成一组正交向量,选择测点时应尽量保证模态向量之间的正交性,通常选用模态置信度矩阵MAC来评价[11],描述为: (6) 如式(6)所示,矩阵的非对角元MACi,j(i≠j)可以评价两模态向量之间的相关性,要保证传感器布置的良好效果,则要求MAC矩阵的非对角元最小作为测点布置的目标函数,其表达式为: minf(x) (7) WMA的传感器优化布置步骤如下: Step1根据式(7)计算猴群的目标函数值f(x)。 Step2参数初始化。包括猴群规模M,初始解正态分布控制的数学期望值μ和方差σ2;爬过程的爬行次数Nc和初始爬步长a;望过程的视野长度b和望次数Nw;跳过程的最大迭代次数Nmax;繁殖进化中的最小后代数Smin、最大后代数Smax、初始标准差σinitial、最终标准差σfinal和非线性调和指数h等。 Step3WMA算法编码及种群初始化。由式(1)初始化猴群位置。 Step4爬过程搜索。由式(2)计算爬行的自适应变步长na,进行爬过程局部搜索。 Step5望过程搜索。确定望区间,产生新望到的位置,若猴子望到更优的解,则更新猴子位置,返回爬过程继续搜索;否则,保持解不变,进行下一步。 Step6跳过程搜索。在跳区间里若跳到更好的解,则更新解,返回爬过程继续搜索;否则,保持解不变,进行下一步。 试验时,光学测试与紧凑断裂拉伸试验同步进行,使用两个1600万像素的CCD相机采集图像,图像采集帧率为4fps。图6(a)为上相机(图3(b)所示的两个相机,一上一下)拍摄的试样4表面散斑图像,在裂尖附近的局部放大散斑图像见图6(b)所示,图像放大率为26pixel/mm。 Step7返回Step 4循环爬过程搜索,直到完成最大跳次数,则进行下一步。 Step8由式(3)计算出每只最优猴子的适应度值φ,筛选出每次迭代中的最优解。 Step9野草繁殖进化。由式(4)确定后代数目Ns,不超过最大后代数Smax。 Step10根据式(5)计算σiter,以正态分布方法初始化子代猴群。 Step11野草竞争排斥。让子代与父代共同竞争,筛选出适应度高的个体保留到下一代中,生成规模为Smax的新猴群,超出最大规模数目且适应度低的猴子将被淘汰。 Step12对新猴群再次进行爬、望、跳三个基本过程搜索。首先进行自适应爬过程,然后进行望过程搜索。若猴子望到更好的解,则更新猴子位置,返回爬过程继续搜索;否则保持解不变,进入下一步跳过程。 Step13在跳区间中,若猴子跳到更好的解,则更新这个解,返回Step 12;否则,保持解不变,进入下一步。 Step14判断算法是否达到最大迭代次数Nmax,若未达到,返回Step 4进行下一轮迭代;否则进入下一步。 图2为WMA的执行步骤和具体流程。 为了验证算法的有效性,选用常用的8个测试函数对WMA进行测试[13,14]。测试函数如表1所示。 Figure 2 Flow chart of WMA图2 WMA流程图 测试函数可行域f1(x)=-20exp(-0.21n∑ni=1x2i)-exp(1n∑ni=1cos(2πxi))+20+exp(1)xi∈-32,32[]f2(x)=∑ni=1x2ixi∈-100,100[]f3(x)=∑ni=1x2i4000-∏ni=1cos(xii)+1xi∈-600,600[]f4(x)=∑ni=1(x2i-10cos(2πxi)+10)xi∈-5.12,5.12[]f5(x)=∑ni=1xi+0.5()2xi∈-100,100[]f6(x)=∑ni=1ix4i+random[0,1)()xi∈-1.28,1.28[]f7(x)=∑n-1i=1100(x2i-xi+1)2+(xi-1)2[]xi∈-5,10[]f8(x)=1200n∑ni=1x2i-∏ni=1cosxix+1()+1.0xi∈-25,25[] 其中,f1(x)、f2(x)是有全局唯一极小点的单模态函数,可用于测试算法的收敛精度和速度;f3(x)、f4(x)是有多个极值的非线性多模态函数,可用于测试算法的全局寻优能力;f5(x)是不连续阶梯函数,与连续函数相比较,用来检验算法的有效性;f6(x)是一个四次函数,用来进一步检验算法的有效性;f7(x)是用来测试算法性能的变态函数;f8(x)是一个多谷函数,搜索过程非常复杂,用来测试算法的全局寻优能力。 由于参数设置的不同将直接影响到计算结果,因此,对WMA算法的猴群规模、最大后代数目、视野长度等重要参数进行分析。分别设置猴群规模为10、20、40,最大后代数为25、50、100,视野长度为0.25、0.5、1.0等三种水平情况,其他参数保持不变,其参数分析结果如表2所示。 Table 2 Analysis result of relevant parameters表2 相关参数分析结果 由表2可以看出:(1)猴群规模的增大会使目标函数值逐步减小。当猴群规模增大到40左右时,目标函数值的下降不明显。同时种群规模的增大使收敛速度下降,计算量增大。(2)最大后代数的选择要适宜,过小不能充分起到将优秀猴子特征信息扩充的作用,过大会增加猴群规模,增大计算量。(3)视野长度的选择要适宜,过大容易使猴子跳步长过冲,过小会降低搜索效率,同时使计算量增大。为此,综合考虑以上因素,选择猴群规模为20,视野长度为0.5,最大后代数为50。 为了验证WMA算法的改进效果,将之与SMA进行对比。两种算法的参数初始化设置如表3所示。 Table 3 Parameter settings表3 参数设置 所有上述算法均通过Matlab2009b进行编码。测试过程中设置测试函数的迭代次数为100次,测试函数的求解结果取50次迭代的平均值,如表4所示。 由表4求解结果来看,改进后的WMA性能优于SMA。由于WMA算法增加了野草繁殖等环节,与SMA算法相比耗时较多,但是差别并不明显,时差保持在1.2 s之内,有些耗时甚至基本相同。因此,从耗时角度来看,改进后的算法并未耗费大量的运算时间。为了对比WMA和SMA收敛情况,对程序运行了100次,统计结果如图3所示。统计结果表明,在100次实验中,WMA收敛结果完全优于SMA(为78%),WMA完全劣于SMA的只有9%。智能优化算法的运算结果存在随机性,WMA的性能在统计意义上优于SMA。在图4进一步对比了迭代100次过程中WMA与SMA的收敛趋势。 Figure 3 Statistical results of program run 100 times图3 程序运行100次的统计结果 WMA在迭代8次左右之后搜索效率迅速提高,收敛精度明显高于SMA。SMA在迭代43次后优化值保持在0.115 6,而WMA在迭代40次后解就收敛到0.095 3,WMA较之SMA收敛精度提高了20.03%。 为了进一步验证WMA的性能,实验中将其与IWO、粒子群算法PSO(Particle Swarm Optimization)和差分进化算法DE(Differential Evolution) Table 4 Test function results表4 测试函数求解结果 Figure 4 Curve of convergence comparison between WMA and SMA图4 WMA与SMA收敛曲线对比图 进行比较[15,16]。设置WMA、PSO、DE、IWO算法的迭代次数均为100次,PSO算法粒子数p=20,粒子最大速度vmax=0.5,学习因子c1=c2=1.45,DE算法种群规模q=20,缩放因子f=0.5,交叉概率cr=0.8,IWO算法种群规模r=20,最小后代数、最大后代数、后代初始标准差、后代最终标准差和非线性调和指数等参数取值同表3。图5给出了4种算法的收敛对比曲线。 Figure 5 Curve of convergence comparison among WMA,PSO,DE, and IWO图5 WMA与PSO、 DE、IWO算法收敛曲线对比图 从图5可以看出,在其他条件相同的情况下,WMA与PSO、DE、IWO进行对比,WMA算法在收敛速度和收敛精度上都明显优于其他算法。 结合表4、图3~图5可知,WMA的搜索能力明显增强,收敛精度大幅提升,该算法在传感器的优化布置中具有一定的实用价值。 纸纱复合袋糊底机主要由涂胶机构、压痕机构、定型机构等组成,工艺流程多、结构复杂,其功能是实现纸纱复合袋的糊底工作[17]。涂胶机构实现纸纱袋袋底的均匀涂胶和粘合,直接决定着产品质量是否合格,在整个工艺流程中起到关键作用。因此,对其进行传感器的优化布置,获取其运行振动参数,为相关人员及时反馈相关信息,可确保机器稳定、高效和安全运行[18 - 20]。 为了检验本文所提算法的有效性,以糊底机涂胶机构为例,采用WMA进行传感器的优化布置。 涂胶机构是纸纱复合袋糊底过程中传递、涂胶的机构,由印胶辊、粘胶辊、匀胶辊、转动齿轮和胶槽等组成。机构尺寸为860×500×580(长×宽×高)mm。辊子材料选用灰铸铁,弹性模量1.2×105Mpa,泊松比0.25。支撑板材料为45钢,弹性模量2.0×105Mpa,泊松比0.3。涂胶机构总质量为167.25 kg。 用SolidWorks对涂胶机构进行三维实体建模,并用ANSYS软件进行模态分析。在图6的有限元模型中,辊子采用管单元(PIPE16),支撑板及其它组件采用单轴受力单元(BEAM4)。涂胶机构共划分为42 041个节点,14 469个单元[10]。 Figure 6 Finite element order model of gelatinize agency图6 涂胶机构有限元模型 在纸纱复合袋糊底机的工艺要求中,印胶辊的转速为21.8 r/min、匀胶辊和粘胶辊的转速均为32.2 r/min,三个辊的传输功率均为0.67 kW。扭矩公式为: (8) 其中,P(kW)为功率,T(N·m)为扭矩,n(r/min)为转速。 与印胶辊和粘胶辊相较,匀胶辊反向转动。由式(8)算得各辊子的扭矩分别为T印=198.72N·m,T匀=-293.51N·m,T粘=293.51N·m。确定底板安装部位为边界条件,施加扭矩和重力加速度载荷,测出涂胶机构前10阶模态固有频率,详见表5[10]。 Table 5 The first 10 orders modalfrequency of gelatinize agency表5 涂胶机构前10阶模态频率 由上述计算的42 041个节点在模态分析中自由度数目计算量过大。在考虑保留主要结构形态的情况下对模型进行必要的简化,如图7所示[10]。 Figure 7 Simplified model of gelatinize agency图7 涂胶机构简化模型 Figure 8 Curve of MAC variation图8 MAC值变化曲线 Table 6 Scheme of sensor placement表6 传感器布设方案 表6所示传感器布置方案可有效获取涂胶机构的运行参数,达到了预期目的,进一步证明了WMA的有效性。 本文在SMA的基础上引入IWO的繁殖进化和竞争生存过程,提出了WMA优化算法并将其应用于传感器优化布置中。以典型的测试函数验证其有效性,通过与其他算法的比较验证其性能的改进,最后以糊底机涂胶机构为对象进行传感器优化布置,得出如下结论: (1)该算法在SMA的基础上,通过正态分布方式初始化猴群,使得猴群的多样性得到了提高;采用自适应步长的爬过程,使得算法的搜索精度和收敛速度进一步提高;引入野草繁殖进化因子,在后代种群繁殖中扩大优秀猴子的影响范围;引入竞争排斥机制,将子代与父代混合后共同竞争形成新的猴群再进行猴群搜索,进一步提高了算法的求解精度。 (2)以8个典型的测试函数验证了WMA的有效性。通过与PSO、DE及IWO等算法的比较验证了WMA收敛性的改善。 (3)将WMA应用于传感器优化布置中,以糊底机涂胶机构为对象进行方案的实施,根据涂胶机构的应用实际和优化结果表明,WMA求解精度较SMA有大幅提高。 参考文献: [1] Yi Ting-hua, Zhang Xu-dong,Li Hong-nan.Collaborative-climb monkey algorithm for optimal sensor placement[J].Chinese Journal of Computational Mechanics,2014,31(6):681-686.(in Chinese) [2] Mehrabian A R,Lucas C.A novel numerical optimization algorithm inspired from weed colonization [J].Ecological Informatics,2006,1(4):355-366. [3] Han Yi,Cai Jian-hu,Li Yan-lai,et al.Invasive weed optimization and its advances[J].Computer Science,2011,38(3):20-23.(in Chinese) [4] Zhao Rui-qing,Tang Wan-sheng.Monkey algorithm for global numerical optimization[J].Journal of Uncertain System,2008,2(3):164-175. [5] Zhang Jia-jia. An intrusion detection method based on monkey algorithm[D].Tianjin:Tianjin University,2010.(in Chinese) [6] Wang Jing-ran,Yu Yi-xin,Zeng Huan.Discrete monkey algorithm and its application in transmission network expansion planning[J].Journal of Tianjin University,2010,43(9):798-803.(in Chinese) [7] Yi Ting-hua,Li Hong-nan,Zhang Xu-dong.A modified monkey algorithm for optimal sensor placement in structural health monitoring[J].Smart Materials and Structures,2012,21(10):article ID 105033. [8] Zhang Xu-dong.Optimal sensor placement based on monkey algorithm[D].Dalian:Dalian University of Technology,2013.(in Chinese) [9] Zhang Ya-jie.Research on monkey algorithm and its application [D].Xi’an:Xidian University,2014.(in Chinese) [10] Du Guo-zhang,Ma Li.Application of improved monkey algorithm in optimal placement of sensor[J].Transducer and Microsystem Technologies,2015,34(8):152-155.(in Chinese) [11] Came T G,Dohmann C R.A modal test design strategy for modal correlation[C]∥Proc of the 13th International Modal Analysis Conference,1995:927-933. [12] Wei Xiu-ye,Pan Hong-xia,Huang Jin-ying.Study on sensor optimal layout for gearbox[J].Acta Armamentarii,2010,31(11):1508-1513.(in Chinese) [13] Liu Yan,Liu Gui-jie,Liu Bo.Research status and prospect on optimal placement of sensor[J].Transducer and Microsystem Technologies,2010,29(11):4-13.(in Chinese) [14] Han Jian-quan,Mao Li,Zhou Chang-xi.Artificial bee colony algorithm based on improved local search strategy[J].Journal of Frontiers of Computer Science and Technology,2015,9(6):761-767.(in Chinese) [15] Xu Bin.Research and application of multi-objective optimization algorithms based on differential evolution [D].Shanghai:East China University of Science and Technology,2013.(in Chinese) [16] Xu He-ming.Research on multi-objective particle swarm optimization algorithms[D].Shanghai:Shanghai Jiao Tong University,2013.(in Chinese) [17] Wang Yi-bing,Peng Zhen-rui,Yin Hong,et al.Design of the control system for paper and yarn compounded bag bottom-pasting machine[J].Manufacturing Automation,2015,37(1):123-126.(in Chinese) [18] Zhao Yu. Optimal sensor placement for bridge structural health monitoring based on intelligence algorithm [D].Lanzhou:Lanzhou Jiaotong University,2014.(in Chinese) [19] Bansal J C,Sharma H,Jadon S S.Spider monkey optimization algorithm for numerical optimization[J].Memetic Computing,2014,6(1):31-47. [20] Yi Ting-hua,Li Hong-nan,Zhang Xu-dong.Health monitoring sensor placement optimization for canton tower using immune monkey algorithm[J].Structural Control and Health Monitoring,2015,22(1):123-138. 附中文参考文献: [1] 伊廷华,张旭东,李宏男.基于协同爬猴群算法的传感器优化布置方法研究[J].计算力学学报,2014,31(6):681-686. [3] 韩毅,蔡建湖,李廷来,等.野草算法及其研究进展[J].计算机科学,2011,38(3):20-23. [5] 张佳佳.基于猴群算法的入侵检测技术研究[D].天津:天津大学,2010. [6] 王靖然,余贻鑫,曾浣.离散猴群算法及其在输电网扩展规划中的应用[J].天津大学学报,2010,43(9):798-803. [8] 张旭东.基于猴群算法的传感器优化布置方法研究[D].大连:大连理工大学,2013. [9] 张亚洁.猴群算法及其应用研究[D].西安:西安电子科技大学,2014. [10] 杜国璋,马丽.改进的猴群算法在传感器优化布置中的应用[J].传感器与微系统,2015,34(8):152-155. [12] 魏秀业,潘宏侠,黄晋英.齿轮箱传感器优化布置研究[J].兵工学报,2010,31(11):1508-1513. [13] 刘艳,刘贵杰,刘波.传感器优化布置研究现状与展望[J].传感器与微系统,2010,29(11):4-13. [14] 韩建权,毛力,周长喜.基于改进局部搜索策略的人工蜂群算法[J].计算机科学与探索,2015,9(6):761-767. [15] 徐斌.基于差分进化算法的多目标优化方法研究及其应用[D].上海:华东理工大学,2013. [16] 徐鹤鸣.多目标粒子群优化算法的研究[D].上海:上海交通大学,2013. [17] 王义兵,彭珍瑞,殷红,等.纸纱复合袋糊底机控制系统设计[J].制造业自动化,2015,37(1):123-126. [18] 赵宇.基于智能算法的桥梁结构健康监测传感器优化配置研究[D].兰州:兰州交通大学,2014.2.3 望过程


2.4 跳过程
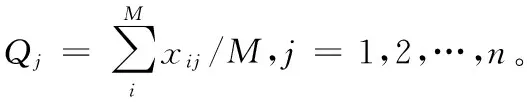

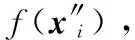
2.5 繁殖进化

2.6 竞争排斥
3 WMA的传感器优化布置
3.1 优化目标函数的选择

3.2 WMA的传感器优化布置步骤
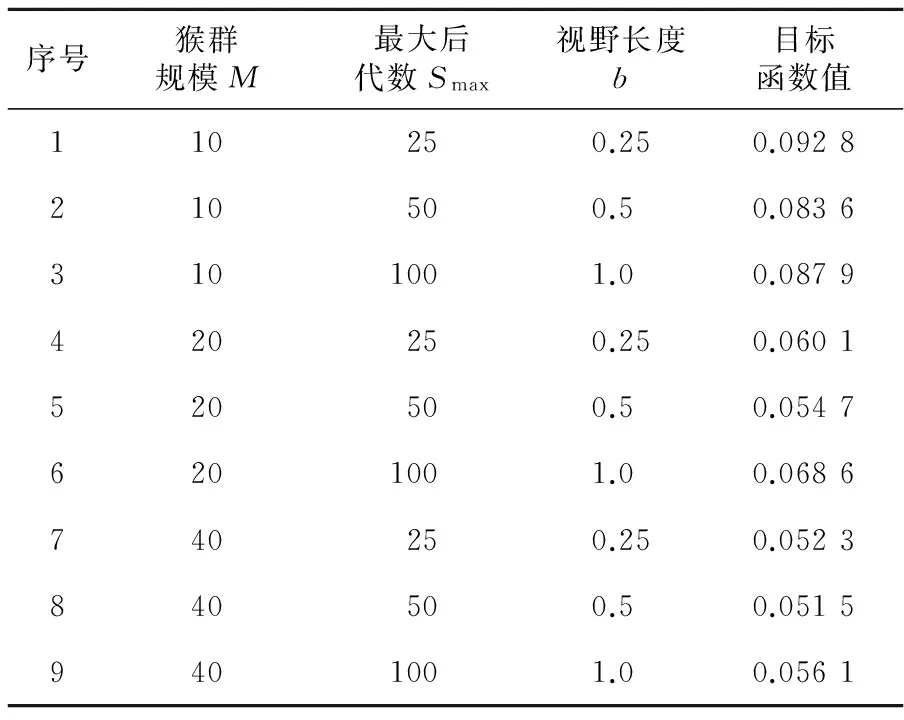
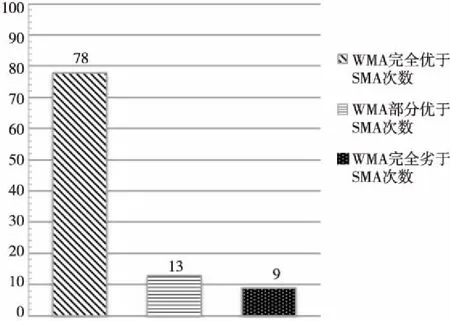
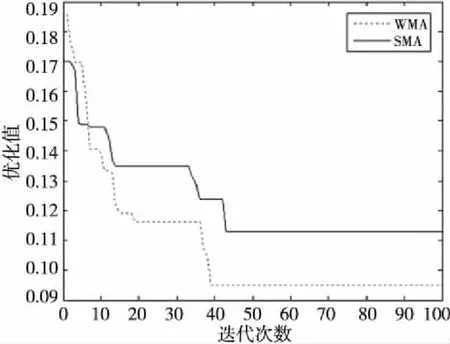
4 测试结果对比分析





5 WMA的传感器优化布置应用实例
5.1 涂胶机构算例模型
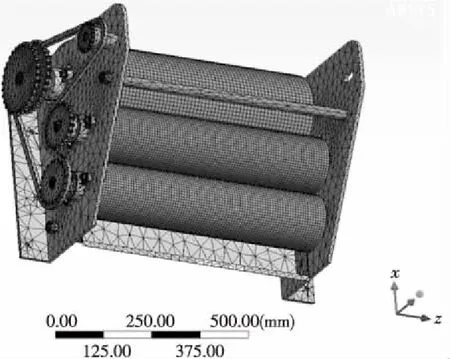
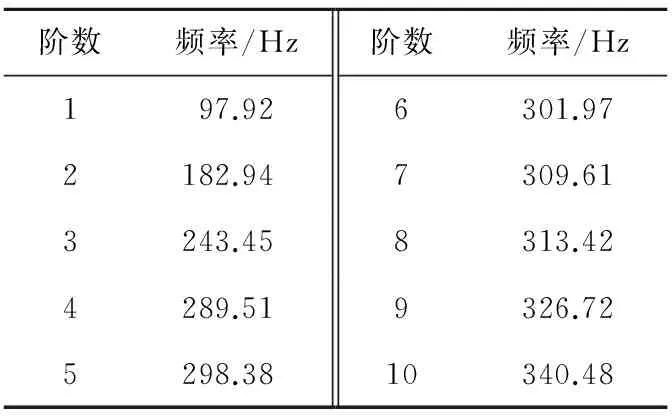
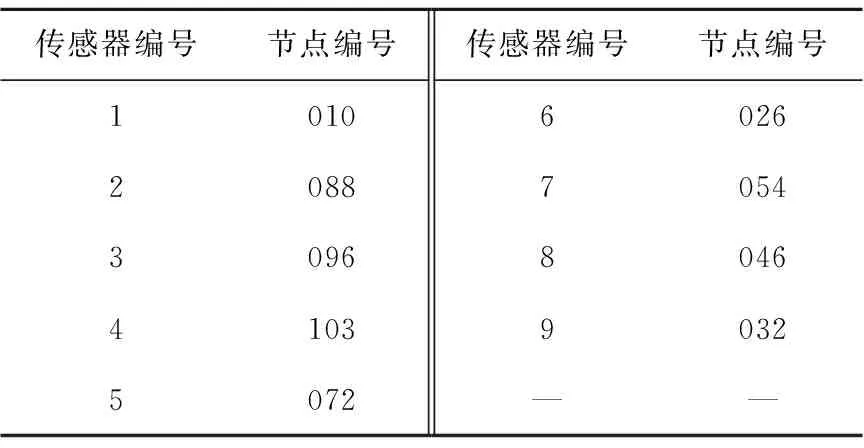
5.2 算例结果分析


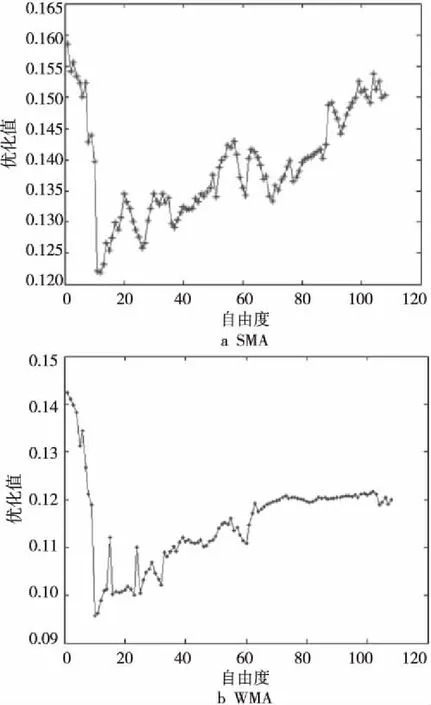
6 结束语
