基于时域梯度相似度的视频质量评价模型*

邱 亮，夏慧明，储久良

(1.南京师范大学泰州学院，江苏 泰州 225300;2.南京理工大学泰州科技学院，江苏 泰州 225300)

1 引言

视频质量评价算法主要分为视频主观质量评价与客观质量评价。由于视频主观评价结果最准确可靠，因此常用视频客观评价结果与主观评价结果的一致性作为客观评价算法的性能评价指标。

目前国际上存在多种视频质量评价算法，峰值信噪比PSNR(Peak Signal Noise Ratio)由于数据模型简单，是一种广泛使用的图像与视频质量评价指标，但该模型与人眼视觉特性的一致性差；Wang等[1]利用结构相似性算法SSIM(Structure SIMilarity)提取场景中的结构特征，并结合亮度掩蔽特性和运动估计，提出基于视频结构相似度测量VSSIM(Video Structural SImilarity Measurement)算法[2]；Seshadrinathan等[3]利用Gabor滤波器对图像进行多通道分解，对各通道进行运动估计，提出了基于运动的视频完整性评价MOVIE(MOtion-based Video Integrity Evaluation index)算法；Prison等[4]提取视频中人眼能够感知的图像特征(亮度、色彩、时空变化)，利用统计学原理模拟人眼视觉系统HVS(Human Visual System)，提出了视频质量评价VQM(Video Quality Model)模型。Lin等[5]利用图像的相位一致性以及图像的空域梯度特征，提出了一种特征相似度测量FSIM(Feature SIMilarity index for image quality assessment)[6]算法，该算法复杂度低、执行效率高，得出的评价结果和人眼主观感受的一致性较好，是目前最好的静态图像质量评价算法之一。

由于人眼的对比度掩蔽特性，人眼对于视觉信号中不同对比度具有较强的敏感度，而梯度信息可以体现图像中的对比度信息。Wang Yue等[7]引入三维Sobel算子计算视频的局部时空域的梯度，对时空域梯度幅值进行阈值判断选取感兴趣像素点，然后计算感兴趣区域的3D结构张量来描述视频的时域失真，取得了较好的视频质量评价效果。

本文借鉴FSIM在空域计算梯度相似度的方法，并利用视频序列前后几帧的相关性，采用一种新的时域三维Sobel算子计算时域梯度相似度，提出了一种基于时域梯度相似度矩阵的视频质量评价模型TGSM-FSIM(video quality assessment model based on Temporal domain Gradient Similarity Matrix and FSIM)。该模型不局限于特定的视频主观评价数据库，具有计算复杂度低、通用性强等特点，并且对不同失真类型的视频序列均有较好的视频评价性能，因此算法有较好的鲁棒性。

2 基于时域梯度相似度的视频质量评价模型

与静态图像相比，视频序列存在一些复杂的时域变化，因此本文在FSIM图像评价算法中加入时域梯度相似度来描述视频的时域失真。

2.1 FSIM算法

FSIM算法是一种基于视觉浅层次特征的图像评价算法，主要基于图像的相位一致性特征与图像的空域梯度特征。

相位一致性特征相似度矩阵计算公式为：

(1)

其中,PC(x)表示图像的相位一致性矩阵，计算过程参见文献[7]，T1是一个常数。

利用空域的梯度算子计算出图像垂直梯度的特征函数Gy(x)与水平方向梯度的特征函数Gx(x)，该算法采用的是Scharr算子，如表1所示。

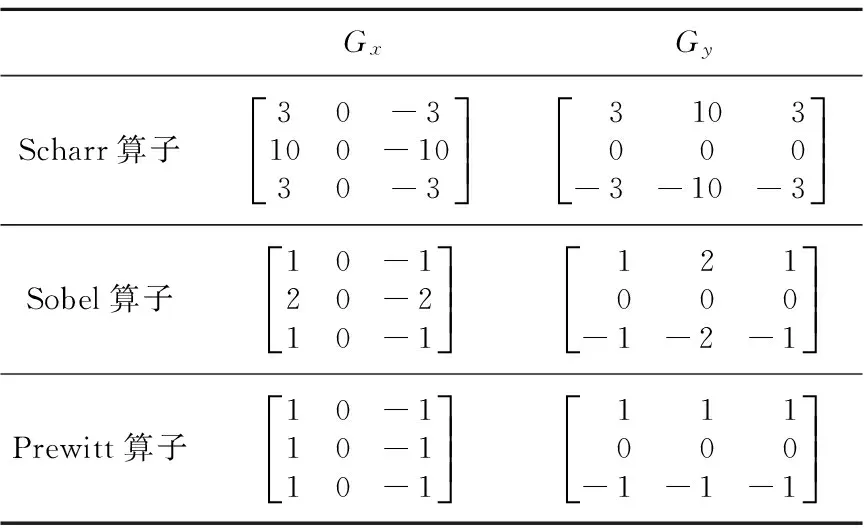
Table 1 Gradient operators表1 梯度算子

图像空域梯度幅值矩阵计算公式为：

(2)

图像空域梯度相似度矩阵计算公式为：

(3)

其中,T2为常数。

结合相位一致性与梯度特征，得到参考图像与失真图像相似度矩阵计算公式为：

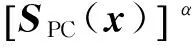
(4)

其中,α、β为常数。

像素的相位一致性值可以反映该像素为人类视觉感兴趣像素区域的可能性，因此用相位一致性值作为SL(x)的加权系数得到质量评价模型，如式(5)所示：

(5)

其中，Ω表示整个空域，PCm(x)表示参考图像与失真图像矩阵对应矩阵元素的较大值矩阵，可以表示为：

PCm=max(PC1(x),PC2(x))

(6)

2.2 时域梯度相似度矩阵

二维梯度算子没有考虑时域的梯度信息，文献[7]引入三维梯度算子计算时域结构张量矩阵，取得了较好的视频质量评价性能。本文将FSIM的空域Scharr算子进行扩展，形成三维梯度算子，如图1所示。

Figure 1 Three-dimensional gradient operator图1 三维梯度算子

Figure 3 Progress of calculating gradient similarity matrix图3 梯度相似度矩阵计算示意图

令ft(x)表示当前帧，ft-1(x)表示当前帧的后一帧，ft+1(x)表示前一帧。利用图1中的三维梯度算子，计算时域梯度的公式为：

Gt(x)=gt-1*ft-1(x)+

gt*ft(x)+gt+1*ft+1(x)

(7)

但是,对于视频编码标准，如H.264编码标准，一般采用两帧以上图像作参考帧进行运动估计与运动补偿，因此，本文在图1的三维梯度算子基础上提出了一种基于前后两帧的三维梯度算子，即对图1的三维梯度算子进行了扩展，并且距离当前帧越远则序列间的时域影响会越小，基于此种特性，本文提出了一种新型的三维梯度算子，如图2所示。

Figure 2 Temporal gradient operator图2 时域梯度算子

(8)

再利用前文所述的方法，计算当前帧的水平梯度Gx(x)与垂直方向的梯度Gy(x)，那么时空域的梯度幅度计算公式为:

GM′(x)=

(9)

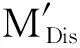
(10)

其中,T3为常数。

本文选取了LIVE视频数据库中“Rushhour”的5个视频序列，时空域梯度相似度矩阵的计算过程如图3所示。

2.3 基于时域梯度相似度的质量评价模型

该模型计算公式为：

TGSM-FSIM=

(11)

3 实验与结果分析

3.1 视频数据库的选取

本文选用LIVE视频主观评价质量数据库[8]进行算法的性能测试。LIVE视频数据库是目前最新的且被广泛认可的视频主观评价数据库[9]，包含了10个原始视频序列，视频序列的分辨率为768×432,其中7个视频序列帧率为25 fps，3个视频序列帧率为50 fps。每一个原始视频序列对应4种不同失真类型与失真程度共15个失真序列，其中4个无线失真，3个IP失真，4个H.264压缩和4个MPEG-2压缩。

3.2 算法性能评价指标

客观图像/视频质量评价算法的性能评价主要衡量客观评价数据与主观评价数据的一致性。视频质量专家组VQEG(Video Quality Experts Group)提出了四种评价指标：斯皮尔曼等级次序相关系数SROCC(Spearman Rank Order Correlation Coefficient)、肯德尔等级次序相关系数KROCC(Kendall Rank Order Correlation Coefficient)、皮尔森线性相关系数PLCC(Pearson Linear Correlation Coefficient)和均方根误差RMSE(Root Mean Square Error)。本文选取SROCC与PLCC作为视频质量评价算法性能的指标。

SROCC计算公式为：

(12)

其中,di表示第i个视频序列在主观评价分数中的排序与客观评价分数中排序的差值。

对于PLCC的计算，首先要对主观数据与客观数据进行非线性拟合，文献[10]给出了一种Logistic函数对数据进行拟合：

(13)

其中，βi是需要拟合的参数。

PLCC计算公式为：

(14)

3.3 实验结果与分析

为了更好地评价本文所提视频质量评价算法，将该算法与经典的VSSIM、MOVIE和VQM等算法在LIVE视频数据库上进行性能对比。表2给出了PLCC与SROCC指标，其中VSSIM、MOVIE、VQM等三种算法的PLCC与SROCC指标参考了文献[7]中的数据。采用FSIM对视频质量评价时，首先分别计算失真序列每一帧的质量，然后计算平均值作为视频序列的质量。TGSM-FSIM1采用图1中的三维梯度算子计算时域梯度，TGSM-FSIM2采用本文提出的前后多帧的新三维梯度算子计算时域梯度。

从表2可看出，本文所提视频质量评价算法与目前经典的三种算法相比，本文算法性能最好，其中SROCC比MOVIE算法高出约3%，比VQM高出11%。并且MOVIE算法是基于三维Gabor滤波分解到多时空通道，算法复杂度远远高于本文的算法。因此，从计算复杂度上来说，本文算法较MOVIE算法有优势。与FSIM算法相比，本文所提算法由于引入了时域梯度相似度矩阵，在原FSIM算法提取空域梯度的基础上加入了时域的梯度信息，可以较好地表示视频的时域变化，因此视频评价性能有较大提高，PLCC提高了约10%，SROCC提高了约9%。

表3给出了本文算法对不同失真类型视频的评价性能。由表3可看出，本文提出算法模型在对各种失真类型视频进行质量评价时都具有很好的鲁棒性，对各种失真类型的评价性能PLCC指标均在0.75以上，其中对无线失真的视频评价性能最好，评价IP失真性能次之，MPEG2的评价性能最差。

Table 3 Assessment performance ofthe TGSM-FSIM in different distortion types表3 TGSM-FSIM对不同失真视频的评价性能

图4为本文所提视频质量评价模型与LIVE数据库中主观评分MOS(Mean Opinion Score)的一致性对比图。图4中离散点表示LIVE数据库中所有失真序列，一共有150个离散点，实线是Logistic函数对视频序列的客观评价结果与主观数据的非线性拟合曲线。离散点如果均匀分布在拟合曲线上则认为评价算法性能较好。

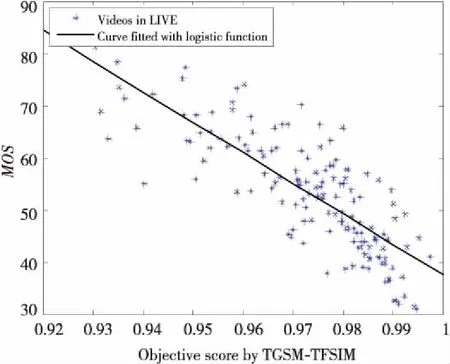
Figure 4 TGSM-FSIM algorithm and MOS data fitting curve图4 TGSM-FSIM算法与MOS数据拟合曲线

由图4可以看出，本文提出的评价模型与主观视频评价结果具有较好的一致性。

4 结束语

本文在FSIM算法中加入了时域梯度相似度矩阵，将图像质量评价的二维梯度模型改进为视频质量评价的三维梯度模型，提出了基于时域梯度相似度矩阵的视频质量评价算法，与人眼主观视频质量评价取得了较好的一致性，并且算法并不需要复杂的变换域变换，计算复杂度低，可以实现实时的视频质量评价。

参考文献:

[1] Wang Z, Bovik A C, Sheikh H R,et al.Image quality assessment:From error visibility to structural similarity [J].IEEE Transactions on Image Processing,2004,13(4):600-612.

[2] Wang Zhou, Lu Li-gang, Bovik A C. Video quality assessment based on structural distortion measurement [J].Signal Processing-Image Communication,2004,19(2):121-132.

[3] Seshadrinathan K, Bovik A C. Motion tuned spatio-temporal quality assessment of natural videos [J].IEEE Transactions on Image Processing,2010,19(2):335-350.

[4] Pinson M H,Wolf S.A new standardized method for objectively measuring video quality [J].IEEE Transactions on Broadcasting,2004,50(3):312-322.

[5] Morrone M C,Owens R A.Feature detection from local energy [J].Pattern Recognition Letters,2014,6(5):303-313.

[6] Zhang Lin, Zhang Lei, Mou Xuan-qin,et al.FSIM:A feature similarity index for image quality assessment [J].IEEE Transactions on Image Processing,2011,20(8):2378-2386.

[7] Wang Yue, Jiang Ting-ting, Ma Si-wei,et al.Novel spatio-temporal structural information based video quality metric [J].IEEE Transactions on Circuits & Systems for Video Technology,2012,22(7):989-998.

[8] Seshadrinathan K, Soundararajan R, Bovik A C,et al.Study of subjective and objective quality assessment of video [J].IEEE Transactions on Image Processing,2010,19(6):1427-1441.

[9] Rohaly A,Libert J,Corriveau P,et al.Final report from the video quality experts group on the validation of objective models of video quality assessment[R].[S.l]:ITU-T Standards Contribution COM,2000:9-80.

[10] Sheikh H R, Sabir M F, Bovik A C. A statistical evaluation of recent full reference image quality assessment algorithms [J].IEEE Transactions on Image Processing,2006,15(11):3440-3451.