具有消息恢复功能的格身份签名方案*

阚元平

(福建师范大学福清分校电子与信息工程学院，福建 福清 350300)

1 引言

基于身份的数字签名IBS(Identity-Based Signature)由Shamir[1]于1984年首次提出，其特点是用户公钥可以是标识用户身份的任意字符串，如用户的电子邮件地址等，因此避免了传统公钥体制的密钥管理问题。第一个实用的IBS方案由Boneh和Franklin[2]于2001年利用双线性对提出，但其计算复杂度较高。IBS作为在轻量级应用领域的重要技术，在电子商务、电子政务、云计算等领域具有广泛的应用前景。

目前，IBS方案大多基于传统密码体制，而随着量子计算机的发展，传统密码体制面临重大的安全隐患——量子算法攻击。1996年,Shor[3]指出,基于离散对数问题和大数分解问题的密码体制可由量子计算机在多项式时间内求解，因而基于双线性对的密码算法也不再安全。考虑到量子计算的发展情形[4]，寻找可抵抗量子攻击的IBS方案具有重要意义。

在后量子密码时代，格密码可有效抵抗量子攻击。1996年,Ajtai[5]证明了格困难问题在最坏情形和平均情形的困难性等价规约，2009年,Bernstein[6]指出格密码可抵抗量子攻击。在此基础上，Ckert[7]于2010年提出了首个基于格密码的IBS方案，此后基于格密码的IBS方案大量出现[8 - 12]，其中不乏具有抵抗强伪造攻击的高效格身份签名方案。2016年,Xie等[13]提出了一个高效的NTRU(Number Theory Research Unit)格的IBS方案，其可抵抗选择明文伪造攻击。

1993年Nyberg等[14]提出了消息恢复签名的概念，由于其可减小消息和签名的长度，因而适用于资源受限的轻量级应用领域。2013年,Tian等[15]提出了格消息恢复签名方案，2014年,张襄松等[16]提出了无陷门的格消息恢复签名方案。

本文在Xie等[13]方案基础上，构造一个具有消息恢复功能的格身份签名方案，并给出了安全性证明。本方案具有高效、抵抗伪造攻击、签名长度短的特点，可广泛应用于轻量级认证领域。

2 预备知识

2.1 符号说明[13,15]

安全参数N=2t，为大于8的正整数，其余的参数与之相关。R、Z分别为实数、整数空间。环Rq=Zq[x]/(xN+1)，其中q为大于5的素数，xN+1可分解为kq个模q的不可约多项式。R×为Rq中的可逆元组成的集合，黑体小写字母如x表示向量，黑体大写字母如X表示矩阵，〈x,y〉表示向量内积，‖x‖表示欧式范数。

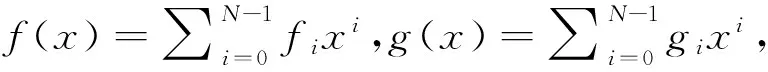
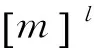
由f生成的矩阵，记为：

2.2 NTRU格

Λh,q={(u,v)∈R2|u+v*h≡0 modq}

NTRU格为2N维实向量空间R2N上满秩的格，同时也是使用范围最广、效率最高的格之一。基Ah,q中IN为N×N阶单位阵，ON为N×N阶元素为0的矩阵。

2.3 离散高斯分布

在N维实向量空间RN上，当以σ>0为标准差，c∈RN为对称中心时：

RN上高斯分布定义为：

格Λ的高斯分布定义为：

格Λ的离散高斯分布定义为：

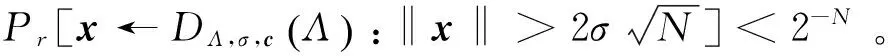
2.4 NTRU格上的小整数解问题

2.5 高斯采样算法

高斯采样函数Gaussian_Sampler(B,σ,c)[17]可在概率多项式时间内输出N维向量v，使其分布与给定的格Λ的离散高斯分布DΛ,σ,c统计近似。

输入：N维格Λ的基B，离散高斯分布标准差σ，中心c′∈ZN。

输出：v←DΛ,σ,c。

1.令vN=0,cN=c′;

2.fori=N…1 do

6.ci-1=ci-zibi,vi-1=vi+zibi;

7.输出v0。

3 具有消息恢复功能的格身份签名方案

本节将在Xie等[13]方案基础上，构造一个具有消息恢复功能的格身份签名方案。下面给出具体的密钥生成、签名生成和签名验证算法。

3.1 系统主密钥生成算法

本算法在指定安全参数N、素数q、方差σ的情况下，输出系统主私钥msk(master secret key)和系统主公钥mpk(master public key)。

输入：N,q∈Z,σ>0。

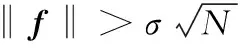
3.若〈f,g〉∉R，重新开始;

4.计算f1,g1∈RN,使其满足f*f1-g*g1=1，令fq=qf1,gq=qg1;

5.用Babai最近平面法计算(f′,g′)，使得存在k∈R满足(f′,g′)=(fq,gq)-k(f,g);

6.若‖(f′,g′)‖>Nσ，重新开始;

3.2 用户私钥产生算法

在本方案中，用户身份id(identification)作为用户的公钥，而用户id的私钥SKid(SecretKey)则由系统根据用户身份id及系统主私钥msk计算而来。因此，系统需要首先验证用户身份并需维护用户密钥列表，当用户注册时，若其选用的用户身份id未被注册，将其放入用户密钥列表，并输出用户私钥SKid；否则用户需重新选择用户身份id后再次注册。系统验证用户身份后，执行如下算法：

输入：用户身份id，系统主私钥msk。

输出：用户私钥SKid=(s1,s2)。

1.若用户身份id已存在于用户密钥列表中，则拒绝，令用户重新选择用户身份id后重新开始;

3.(s1,s2)=Gaussian_Sampler(B,σ,(t,0))，满足s1+s2*h=t;

4.返回SKid=(s1,s2);

系统将SKid=(s1,s2)安全地交付给用户。

3.3 签名算法

签名者用下面的算法，利用自己的私钥SKid对要签名的消息m进行消息可恢复的格身份签名。

输入：用户私钥SKid，消息m。

输出：消息签名(z1,z2,r)及部分消息m2。

1.选择y1,y2∈DZN,s;

2.计算u=H1(y1+h*y2);

3.令m=m1‖m2，其中|m1|=l2，若|m|≤l2，则m2=⊥;

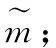
6.计算c=H2(r,m2);

7.计算zi=yi+si*c,i=1,2;

8.以概率min(DZN,s/MDZN,s,SKidu,1) 输出消息签名(z1,z2,r)及部分消息m2。

签名者将消息签名(z1,z2,r)及部分消息m2发送给验证者，而普通签名算法则需传输整个消息m和消息签名，本算法减少了l2比特的传输数据量，因此更适用于轻量级认证领域。

3.4 验证算法

消息验证者收到消息可恢复的格身份签名及部分消息后，利用签名者的公钥即其身份id，用以下算法进行签名的验证。若最终签名能通过验证则输出原始消息m，否则拒绝该签名。

输入：消息签名(z1,z2,r)及部分消息m2，用户身份id。

输出：消息m或拒绝。

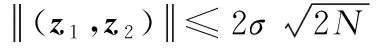
2.计算c=H2(r,m2);

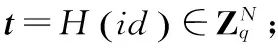
4.计算u=H1(h*z2+z1-t*c);

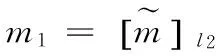
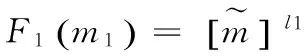
4 安全性分析

本节对上述签名方案的正确性进行证明；给出了本方案在随机预言机模型下的安全性证明，证明了本方案可有效抵抗适应性选择明文和选择身份攻击；最后对签名的有效性做出了分析，说明本方案可有效减少签名传输数据量。因此，本方案具有高效、抵抗伪造攻击、签名长度短的特点，可广泛应用于轻量级认证领域。

4.1 正确性

定理1本方案中签名算法输出的合法有效签名能够通过验证，并恢复完整消息。

证明消息签名(z1,z2,r)及部分消息m2，用户身份id。由上述算法可知：

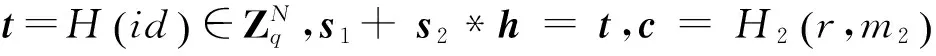
∴h*z2+z1-t*c=h*(y2+s2*c) +y1+s1*c-(s1+s2*h)*c=y1+h*y2

∴H1(h*z2+z1-t*c) =u

□

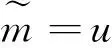
4.2 安全分析

定理2假设NTRU格上的近似最短向量问题无多项式有效求解算法，则本方案在随机预言机模型下可有效抵抗适应性选择明文和选择身份攻击。

证明若存在攻击者A以不可忽略的概率ε=ε(N)攻破本方案，则可构造一个多项式时间的挑战者C,以近似不可忽略的概率ε=ε(N)攻破NTRU格上的近似最短向量问题。

A和C之间的交互如下：

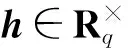
问询：A以如下方式进行问询，一般假定A须在其他问询前首先对身份id问询随机预言机H，其中哈希问询H(id)及对身份id提取问询只能问询一次。

(1)哈希函数H问询：对于身份idi的问询，C查询用户密钥列表ID_list(identification-list)，其初始值为空。若idi存在，则返回相应的H(idi)给A；否则，C均匀随机选择si1,si2∈DZN,s，计算H(idi)=si1+h*si2，并将(idi,Pidi,SKidi=(si1,si2))放入ID_list，将H(idi)作为idi的应答发送给A。

(2)提取问询：给定idi，C查询ID_list寻找与之匹配的SKidi并将其发送给A。

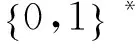
(4)哈希函数F1,F2,H1,H2问询：当A将(idi,mi)发送给C对F1,F2,H1,H2分别或者结合问询，C查询Sign_list找到对应的参数进行返回。

按照如下方式，C可有效解决NTRU上的小整数解问题：

□

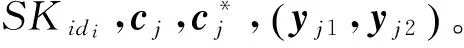
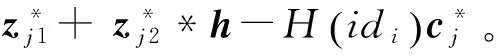
4.3 有效性

本文给出的构造方法可将任意基于NTRU格小整数解问题的身份签名方案改成具有消息恢复功能的格身份签名方案。由于具有消息恢复功能的格身份签名方案为本文首次提出，无法查找相应的文献进行有效的对比分析，因此只对本方案可有效减少签名长度方面进行分析。根据签名过程可知，若原方案签名形式为((z1,z2,n),m),则新签名方案为((z1,z2,r),m2)，本方案签名长度减少|n|+|m|-[(l1+l2)+(|m|-l2)]=|n|-l1比特，不妨设l1=l2=|n|/2比特，则本方案将签名长度有效缩短|n|/2比特。

5 结束语

随着量子计算机的发展，基于大数分解问题及离散对数问题的密码体制已不再安全，但格密码被认为是量子安全的，所以本文在格密码基础上构造了具有消息恢复功能的身份数字签名方案。本方案在随机预言模型下不可伪造，且与普通格身份签名比较，减少了签名长度，效率更高，可以广泛应用于轻量级应用领域。在其他格模型及标准格模型下，构造能抵抗适应性选择身份和消息攻击的消息恢复格身份签名方案是下一步值得研究的工作。

参考文献:

[1] Shamir A. Identity-based cryptosystems and signature schemes[C]∥Proc of Workshop on the Theory and Application of Cryptographic Techniques(CRYPTO 1984),1984:47-53.

[2] Boneh D,Franklin M K.Identity-based encryption from the Weil pairing[C]∥Proc of International Cryptology Conference on Advances in Cryptology,2001:213-229.

[3] Shor P W.Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J].SIAM Review,1996,41(2):1484-1509.

[4] Krenn M,Huber M,Fickler R,et al.Generation and confirmation of a (100×100)-dimensional entangled quantum system[J].Proceedings of the National Academy of Sciences of the United States of America,2014,111(17):6243-6247.

[5] Ajtai M.Generating hard instances of lattice problems[C]∥Proc of the 28th Annual ACM Symposium on Theory of Computing,1996:99-108.

[6] Bernstein D J. Introduction to post-quantum cryptography[M]∥Post-Quantum Cryptography.Berlin:Springer Berlin Heidelberg,2009:1-14.

[7] Ckert M.Strongly unforgeable signatures and hierarchical identity-based signatures from lattices without random oracles[M]∥Post-Quantum Cryptography.Berlin:Springer Berlin Heidelberg,2010:182-200.

[8] Xiang Xin-yin. Identity-based forward secure signature scheme from lattices [J].Computer Engineering,2015,41(9):155-158.(in Chinese)

[9] Yang Dan-ting, Xu Chun-gen,Xu Lei,et al.Identity-based signature scheme over ideal lattices [J].Journal of Cryptologic Research,2015,2(4):306-316.(in Chinese)

[10] Yang Chun-li,Yan Jian-hua,Zheng Shi-hui,et al.Analysis and improvement of an identity-based signature scheme from lattices [J].Journal on Communications,2015,36(5):104-111.(in Chinese)

[11] Ducas L,Lyubashevsky V,Prest T.Efficient identity-based encryption over NTRU lattices[C]∥Proc of International Conference on the Theory and Application of Cryptology and Information Security,2014:22-41.

[12] Liu Z,Hu Y,Zhang X,et al.Efficient and strongly unforgeable identity-based signature scheme from lattices in the standard model[J].Security & Communication Networks,2013,6(1):69-77.

[13] Xie J,Hu Y P,Gao J T,et al.Efficient identity-based signature over NTRU lattice[J].Frontiers of Information Technology & Electronic Engineering,2016,17(2):135-142.

[14] Nyberg K,Rueppel R A.A new signature scheme based on the DSA giving message recovery[C]∥Proc of ACM Conference on Computer and Communications Security(CCS’93),1993:58-61.

[15] Tian M,Huang L.Lattice-based message recovery signature schemes[J].International Journal of Electronic Security & Digital Forensics,2013,5(3/4):257-269.

[16] Zhang Xiang-song,Liu Zhen-hua.Non-trapdoors lattice signature scheme with message recovery[J].Computer Science,2014,41(9):165-168.(in Chinese)

[17] Lyubashevsky V.Lattice signatures without trapdoors[C]∥Proc of the 31st Annual International Conference on Theory and Applications of Cryptographic Techniques,2011:738-755.

附中文参考文献：

[8] 向新银.格上基于身份的前向安全签名方案[J].计算机工程,2015,41(9):155-158.

[9] 杨丹婷,许春根,徐磊,等.理想格上基于身份的签名方案[J].密码学报,2015,2(4):306-316.

[10] 杨春丽,闫建华,郑世慧,等.对一个格基身份签名方案的分析和改进[J].通信学报,2015,36(5):104-111.

[16] 张襄松,刘振华.具有消息恢复功能的无陷门格签名方案[J].计算机科学,2014,41(9):165-168.