某柔性空间伞结构展开动态特性研究

阮 洋，陶如意

(南京理工大学 能源与动力工程学院， 南京 210094)

近年来，随着机械、材料以及航空技术的发展，逐渐涌现出用途多样的小型飞行器。小型飞行器以其尺寸小、机动灵活等特点广泛应用于干扰攻击、毁伤评估等军事领域[1-4]以及地质勘探、航空拍摄等民用方面[5-8]。然而小型飞行器因其轻便、体型较小的特点易受外界环境、自身结构变化等的影响，因此，关于小型飞行器优化设计、姿态控制等方面的研究尤为重要。

本文所研究的柔性空间伞结构是由小型固体火箭、折叠织物和刚性骨架所构成的一种轻型柔性空间飞行器。飞行器初始时处于折叠包裹状态，依靠小型固体火箭的推力完成空间释放及展开；其展开过程存在柔性体大变形运动以及多次接触碰撞作用，这些因素很容易引起系统结构的振动，影响飞行稳定性和姿态控制精度，甚至导致空间伞结构失稳、偏航等非预期结果。

目前，对于带有柔性体的飞行器的研究还比较少。有一种模仿鸟类飞行运动的仿生扑翼飞行器[9-10]，对它的研究往往简化成连杆机构而忽略柔性作用；还有一种可变结构柔性翼飞行器[11-12]，其机翼采用铝合金等轻质金属材料，对它的研究处于小变形领域。刘赟等[13]对与本研究有相似机理的空间飞行器的运动过程和姿态控制进行了研究，但没有考虑大变形柔性织物的作用，与实际工作状态有一定差异。从已有的结构动力学研究可以看出，柔性基础的存在对于刚柔耦合结构动力学特性具有重要影响[14]。基于此，本研究以某空间飞行器为研究对象，建立了含织物折叠展开的大变形刚柔耦合模型，对柔性空间伞结构在小型固体火箭驱动下的轴向展开过程进行数值仿真，获得大变形刚柔耦合的柔性空间伞结构的运动规律；分析了小型固体火箭的点火过程对伞结构运动过程的影响，为优化设计和自由飞行阶段的姿态控制提供理论基础和技术指导。

1 柔性空间伞结构释放展开过程运动原理

本文研究的柔性空间伞结构初始时设为折叠包裹状态，如图1所示，被母体投放到指定空间后，由圆筒状展开成如图2所示的伞形。

其释放展开过程的运动原理描述如下：

1) 发射筒脱落：被母体投放到空间后，包裹伞结构的发射筒自行脱落。

2) 径向杆展开：发射筒脱落后引起制动环脱落，六支径向杆约束解除，在扭簧作用下瞬间展开到一定角度。

3) 轴向杆展开：轴向杆是由四根截面不同的方管组成的伸缩杆，杆件间通过楔形垫片连接。径向杆展开后，动力装置(即释放火箭)开始工作，小火箭的推力拉动伸缩杆伸长，杆件间的楔形垫片相互碰撞带动下一根杆运动。同时，折叠织物在伸缩杆的带动下被拉动做大变形运动。

4) 自由飞行：伸缩杆完全伸长后，小火箭继续工作，推力作用带动空间伞结构自由飞行。

释放展开过程中，轴向杆展开过程最复杂。各杆件间的多次碰撞对系统稳定性造成极大考验。同时，具有一定抗弯刚度的柔性织物与刚性体间的相互牵拉作用、柔性织物大变形作用也成为本次研究的难点。本研究以该阶段为研究对象，采用刚柔耦合动力学理论对该问题进行解算。

2 柔性空间伞结构动力学模型建立

2.1 刚柔耦合动力学模型

2.1.1 数学模型

柔性空间伞结构在运动过程中可以看成是26个刚体相互作用的模型，图3是派生系统拓扑构型图。其中，B0为运载母体；B1为支撑底座，Bi(i=2～7)为6只径向支撑杆，Bi(i=8～17)分别为各杆的内垫片、外垫片、杆身，B18为杆连接座，B19为释放火箭，B20为防护伞衣，Hi(1～26)表示为铰，规定铰的方向为背离内接刚体[15]。

根据R-W方法建立各刚体坐标系，设支撑座的坐标系为x0-y0-z0，单位矢量为(i0,j0,k0)，其他各刚体质心处建立坐标系xi-yi-zi(i=1～26)，单位矢量为(ii,ji,ki)，其中各刚体单位矢量分别平行[16]。

派生树系统的关联矩阵S和通路矩阵T分别为

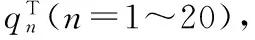
(1)

展开机构刚柔耦合系统的动力学方程为

(2)

其中，A、B分别为含有通路矩阵T的矩阵。

2.1.2 仿真条件

为同时保证伞结构的牢固和轻质，刚性骨架的材料选用铝合金。铰Hi(i=2～7)为旋转副，定义运动方程为STEP(TIME,0,0,0.5,-70D)+STEP(TIME,0.5,0,0.5,0)；铰Hi(i=21～26)也为旋转副，运动方程为STEP(TIME,0,0,0.5,-83.668D)+STEP(TIME,0.5,0,0.5,0)；其余铰均为固定副。系统的驱动力为释放火箭的推力，因此将轴向力定义在B19上，力的大小采用差值函数AKISPL(time,0,Sp1,0)，Sp1为释放火箭沿轴向分布的推力曲线。同时定义各个部件和柔性伞面的接触(FSurface to Surface Contact)、伸缩杆各杆的接触(Surface to Surface Contact)、柔性体自身接触(FSurface to FSurface Contact)。因模型中存在大量接触，计算时间步长设置为1×10-6s。

2.2 柔性伞状织物折叠建模

柔性伞衣在伸展机构的作用下拉展成型，属于被动运动的部件，具有变形大、易牵拉等特点。防护伞衣采用602锦丝66绸，密度为533.77 kg/m3，弹性模量为430.9 MPa，伞厚为0.3 mm。利用圆锥面的几何关系建立如图4所示的柔性伞折叠后的几何模型。采用四边形壳单元划分有限元网格。同时使用固定副(fixed joint)将伞衣固定在刚性骨架上。

3 释放火箭发动机内弹道数值仿真

释放火箭发动机共有4个嵌入式斜切喷管，对称分布在发动机壳体的前端，喷管轴线与发动机的轴线成30°角；燃烧室为两段直径不等的圆柱体组成，如图5所示。

3.1 数学模型

根据质量守恒原理

(3)

建立考虑点火过程的能量守恒方程

(4)

由推力基本公式得出推力的表达式为

(5)

3.2 数值仿真及结果

点火药为颗粒状的2号小粒黑，通常假设为直径为1.25×10-3m的球体。发动机推进剂为两根管状药嵌套的套管式装药结构，以与燃烧室结构相配合。推进剂采用36.4 g的双基推进剂——双铅2，其计算时的临界压力选定为4 MPa。

采用四阶Runge-Kutta法对上述方程进行数值求解，计算得到点火药量为1.0 g时的压力与试验曲线如图6所示。数值计算所得火箭燃烧室平均圧力与实验值吻合较好，表明本文的内弹道模型是合理可靠的。

4 仿真结果及分析

4.1 柔性空间伞结构的动态性能分析

柔性空间伞结构的轴向展开过程包含了伸缩杆垫片间的接触碰撞作用和柔性织物的牵拉作用，是一个复杂的非线性过程，过程中可能含有伸缩杆变形、碰撞振动等情况。伸缩杆在小火箭的推力作用下逐渐被拉出，固定在伸缩杆上的柔性织物也逐渐拉展成伞形。

柔性空间伞结构的拉伸过程包含3个阶段。

第一阶段；变形阶段。小火箭点火后，其推力带动伸缩杆运动，伸缩杆间相契合的内衬楔形垫片相互接触碰撞带动下一根伸缩杆运动，整个过程含有3次垫片碰撞过程，直至伸缩杆全部伸长至1425mm。过程中，柔性织物的大变形运动是最明显的特点。柔性织物具有良好的易牵动易变形的特性，在伸缩杆的带动下极易拉展成形。拉展过程中，其折痕处产生应力集中，随着伸缩杆的拉伸，其形态约束得以释放，应力逐渐消退，如图7所示。

第二阶段：成型且受力运动阶段。伞结构展开成型，做直线运动。该过程伞结构不再有形态的变化，柔性织物的表面应力逐渐消退直至均匀。伸缩杆杆件垫片有断续且轻微的接触碰撞作用，整个系统趋于稳定。在较长的稳定阶段内，柔性织物的应力集中主要在与支撑杆、小型火箭的固定连接处。

第三阶段：自由飞行阶段。小火箭内弹道过程结束后，推力降低为零，飞行系统不再受外力。

在这3个阶段中，包含了丰富而又难以预测的力学过程。小型固体火箭的推力变化导致了杆件间发生了不可预知的多次碰撞，影响着伞结构的稳定性。杆1与杆2、杆2与杆3、杆3与杆4的接触力分别表示为F1、F2、F3，伸缩杆杆件间的接触力大小随时间的变化如图8所示。由图8可知，在20 ms左右，杆1与杆2开始接触，由计结果数据可知F1为213.7 N接触力一直持续直到25.4 ms。杆2和杆3开始接触，F2为197.49 N。37.4 ms附近，F1、F2、F3均发生了突变，这是由于杆4连接了较多的部件，使得杆件需要拉动的部件质量增多，接触力急剧增加，均在10kN左右。拉动杆4及其部件后，接触力变小，稳定在从200 N到300 N之间，并且随着时间有轻微的波动。接触力曲线的波动是因为柔性织物在变形过程中对杆件有一定的牵拉作用，这一影响因素使得杆件的运动过程并不完全平稳。尤其是F3，其波动值最大，它不仅仅受柔性体变形的影响，还与杆4携带的部件有关。杆4携带的部件含有多个旋转铰，径向杆和伞衣连接杆在受到突然拉动后在旋转副的作用下会发生旋转运动，这使得杆4的质量中心发生偏移，杆4与杆3的之间发生忽大忽小的轻微碰撞。

4.2 点火药量对空间伞结构动态特性的影响

小型火箭发动机由于尺寸小，燃烧室的容积较小，点火药量对内弹道过程的影响较为明显，因此点火过程对喷口处的推力大小有较大影响。图9示出了点火药量分别在0.6 g、0.8 g、1.0 g时的推力随时间变化的曲线，曲线走势相近，推力峰值以及结束点因点火药量的不同有明显的区别。点火药量越大，内弹道过程历时越长，推力峰值越大，推力结束的时间越长。其中，点火药量分别在0.6 g、0.8 g、1.0 g时，推力峰值分别达到508.7 N、623.6 N、830.4 N。

4.2.1 对柔性空间伞结构展开时间的影响

柔性伞结构的展开时间是设计研究中考察的主要因素之一。表1中的数据为不同点火药量时柔性伞状结构的展开时间，由表可知，点火药量越大，展开用时越短。点火药量差与展开时间差并不成正比，0.8 g与0.6 g点火药的展开时间差约为4.7 ms，而与1.0 g点火药相差了22.8 ms。

表1 不同点火药量时的展开时间

4.2.2 对柔性空间伞结构振动情况的影响

图10表示了飞行系统在不同点火药下的三阶频率响应。由图10可知，在伸缩杆拉伸阶段，系统的振动最明显，该过程存在多次部件碰撞过程以及柔性体变形过程，是拉伸过程中最不稳定阶段。同时，较大的点火药量会在瞬间产生较大的火箭推力，使杆件间的碰撞力增大。因此，点火药量越大，振动情况越复杂。点火药量的增加或许会带来较高的航速和航程，然而却降低了伞结构的稳定性。在柔性空间伞结构的优化设计中，点火药对振动的影响不容忽视。

5 结论

1) 在柔性伞机构运动过程中，柔性织物与刚性骨架的固定连接处存在应力集中现象，在工程设计中，应考虑对柔性织物的固定连接处加厚。

2) 伸缩杆杆件间的瞬间碰撞力达到14 kN，是持续接触力的近百倍。这对材料的抗拉强度提出了较高要求。

3) 小型固体火箭的点火药量越大，柔性伞机构运动过程中振动情况越复杂。在对柔性伞机构进行稳定性和姿态控制研究中，应综合考察点火药量的影响。

参考文献：

[1] TONY S.TAO.Design and Development of a High-Altitude,In Flight Deployment Micro UAV[D].US:Massachusetts Institute of Technology.

[2] RICHARD T.Martorana.WASP-A High-g Survivable UAV[C].AIAA’s 1stTechnical Conference and Workshop on Unmanned Aerospace Vehicles,2002.

[3] 张爱华.以色列军用小型飞行器发展概览[J].飞航导弹,2010(9)：19-23.

[4] 刘畅.伞降式小型飞行器初始转平飞控制技术研究[D].北京：北京理工大学,2014:1-21.

[5] 廖波.折叠机翼飞行器的发展现状和关键技术研究[J].机械设计,2012,29(4):5-9.

[6] 汪亚真.可变结构小型多旋翼无人飞行器设计与控制研究[D].淮南：安徽理工大学,2016:1-57.

[7] 乔振龙,张晨春,赵振中.小型无人飞行器在内蒙古自治区矿山地质环境动态监测工作中的应用[J].西部资源,2016(6):187-188.

[8] 贾宁,郭建兴.小型无人飞行器与4G图传背包的地震灾情获取与传输[J].地震地磁观测与研究,2016,37(4):163-169.

[9] JOHN M.Dietl,Ephrahim Garcia.Ornithopter optimal trajectory control[J].Aerospace Science and Technology,2013,26(1):192-199.

[10] 张明伟，方宗德，周凯.微型仿鸟扑翼飞机设计与仿真系统开发[J].计算机仿真,2007,24(5):30-33.

[11] 顾鑫.柔性折叠翼飞行器飞行动力学问题研究[D].南京：南京航空航天大学,2012:1-89.

[12] LOH KHEONG,JAMEY JACOB.In flight aspect ratio morphing using inflatable wings[C].46th AIAA Aerospace Science Meeting and Exhibit.Reno,Nevada:AIAA-2008-425,2008.

[13] 刘赟.变结构微小空间飞行器释放与运动特性研究[D].南京：南京理工大学,2013:1-261.

[14] 郭旭,王生.飞艇艇体与推进支架结构耦合动力学仿真分析[J].计算机仿真,2016,33(11):67-72.

[15] 袁士杰.多刚体系统动力学[M].北京：北京理工大学出版社,1992:1-76.

[16] 刘震,毛君,陈洪月.多刚体系统动力学在锚杆机动力学建模中的应用[J].吉林大学学报(信息科学版),2013,31(3):290-296.