翼型对舵翼气动特性的影响分析

杜韩东，李 娜，张康康

(西南技术工程研究所， 重庆 400039)

随着科学技术的发展，21世纪武器装备进入到信息化时代，并朝网络化、精确化、隐身化、立体化、无人化方向发展。精确制导弹药作为各军事大国重要武器装备之一，可大幅提高武器系统的作战效能，已成为世界各国弹药研究的热点[1-2]。目前制导弹药大多采用舵机修正，舵翼气动特性影响弹道修正的效果，因此舵翼设计尤为关键。翼型对舵翼气动特性影响较大，研究不同翼型对舵翼气动特性的影响规律，可为舵翼翼型选型和设计提供依据。目前国内关于翼型研究报道较少，美国国家航空咨询委员会(NACA)开发了NACA系列翼型，有低速翼型、中速翼型和高速翼型，但对于制导弹药，尤其是制导炮弹，由于其结构复杂，加工工艺要求较高，因此一般采用外形简单、易于加工的翼型，较少选用NACA翼型。

1 舵翼模型及计算网格生成

舵翼平面形状采用矩形，弦长为40 mm，展长为60 mm，翼型分别采用菱形、四角形、圆弧形、六角形、削尖矩形和半削尖矩形[3]，见图1。

利用前处理软件建立仿真流场，计算区域采用直径约为33倍展长，高度约为63倍弦长的圆柱体。采用四面体网格对计算区域进行网格划分，并对舵翼表面网格加密，共计网格数量约为25万，部分舵翼表面网格图，如图2。

2 控制方程

控制方程是进行流体仿真的数学模型，主要包括质量守恒方程、动量守恒方程、能量守恒方程以及状态方程[4]。

1) 质量守恒方程，也叫连续性方程

2) 动量守恒方程，即运动方程，也称为Navier-Stokes方程：

3) 能量守恒方程

4) 状态方程

p=p(ρ,T)

相关符号涵义参考计算流体力学相关书籍[5]。

3 计算方法

1) 采用耦合隐式求解法，粘性模型采用Spalart-Allmaras单方程湍流模型，并考虑气动加热；

2) 计算区域材料为空气，并选择理想气体模型，黏度采用三系数的萨兰德模型；

3) 舵翼表面采用无滑移壁面边界条件，仅考虑翼型对气动特性的影响，并假设舵翼表面是光滑的；

4) 计算域外边界采用压力远场边界条件，参考压力为0，远场静压为101 325 Pa；

5) 差分格式中压力插值采用standard方法，压力-速度耦合采用SIMPLEC方法，动量、湍流动能、湍流耗散率均采用二节迎风格式[6-7]；

6) 收敛准则根据阻力系数计算结果判断，当阻力系数波动小于1‰时，认为计算已收敛；

7) 计算工况为：马赫数0.6～2.5，攻角0°和5°。

4 计算结果及分析

根据建立的仿真模型，利用ANSYS Fluent软件对不同翼型的舵翼进行气动仿真[8-9]。在计算气动力系数时，参考面积取翼平面面积；计算弦长方向压心系数时，参考长度取弦长，计算展长方向压心系数时，参考长度取展长[10]。

4.1 阻力特性

不同翼型的舵翼零升阻力系数随马赫数的变化曲线见图3，压差阻力和粘性阻力占全弹阻力百分比随马赫数的变化曲线见图4和图5。不同翼型的舵翼在亚音速和超音速下，压差阻力占全弹阻力的比值见表1。

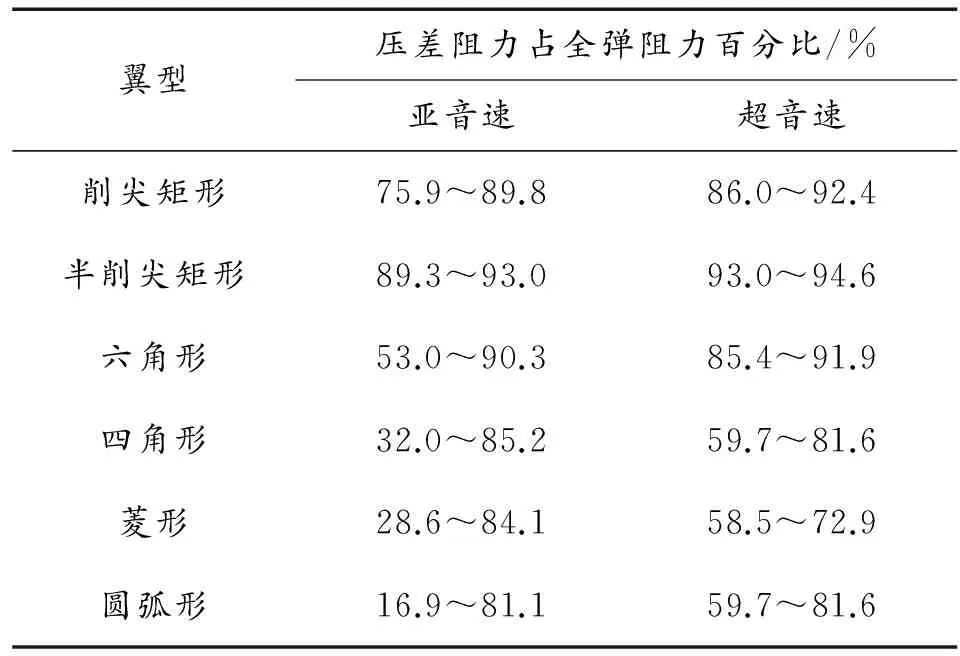
翼型压差阻力占全弹阻力百分比/%亚音速超音速削尖矩形75.9～89.886.0～92.4半削尖矩形89.3～93.093.0～94.6六角形53.0～90.385.4～91.9四角形32.0～85.259.7～81.6菱形28.6～84.158.5～72.9圆弧形16.9～81.159.7～81.6

仿真表明：

1) 不同翼型的舵翼零升阻力系数均随马赫数增大先增大后减小，在1.2马赫附近零升阻力系数达到最大，与实际情况相符。

2) 不同翼型的舵翼的压差阻力占全弹阻力百分比随马赫数的变化规律均为先增大后减小，在音速附近所占比值达到最大；粘性阻力所占全弹阻力百分比随马赫数变化规律与压差阻力的规律相反。

4.2 升力特性及升阻比

不同翼型的舵翼升力系数和升阻比随马赫数的变化曲线分别见图6、图7。

可以看出：

1) 随着马赫数增大升力系数先增大后减小，在1.0～1.2马赫附近达到最大。

2) 半削尖矩形翼型的舵翼升阻比随马赫数增大逐渐减小，其他几种翼型的舵翼升阻比随马赫数的增大先减小后增大，圆弧形、四角形和菱形翼型的舵翼升阻比在音速时最小，约为3.5，六角形和削减矩形翼型的舵翼升阻比在1.5马赫时达到最小，约为1.9。

3) 亚音速时不同翼型的舵翼升阻从大到小为：圆弧形、菱形、四角形、六角形、削尖矩形、半削尖矩形，超音速时升阻比从大到小为：菱形、四角形、圆弧形、六角形、削尖矩形、半削尖矩形。

4.3 压心系数

不同翼型的舵翼弦长方向压心系数和展长方向压心系数随马赫数的变化曲线分别见图8和图9。

仿真表明：

1) 弦长方向压心系数在1.5马赫前变化较大，1.5马赫后变化较小。半削尖矩形的舵翼在弦长方向的压心系数波动最大，其次是削尖矩形和六角形，四角形、菱形和圆弧形波动相对较小。

2) 展长方向压心系数变化较小，压心位置基本在展长的一半处，翼型对展长方向的压心位置影响不大。

5 结论

通过仿真分析，得到不同翼型的舵翼阻力系数、升力系数、升阻比、压心等气动参数随马赫数变化的规律。在制导弹药舵翼设计时，可根据弹丸飞行马赫数范围、射程指标以及舵机扭矩等选择合适的翼型，最大限度减小阻力、增大升阻比，减小压心变化范围，实现舵翼气动性能最优。

注：“舵翼表面粗糙度”与机械零件经过机械加工后的粗糙度相同，其大小参照GB/T 1031—2009。“舵翼表面粗糙度为0.5”即指零件表面轮廓的算术平均偏差(用Ra表示)为0.5 μm，机械加工中需要精加工才能达到。

参考文献：

[1] 邓泽生.21世纪高技术局部战争趋势[M].长沙：国防大学出版社，1962.

[2] 王颂康.高新技术弹药[M].北京：兵器工业出版社，1997.

[3] 沈仲书.弹丸空气动力学[M].北京：国防工业出版社，1984.

[4] 王福军.计算流体动力学分析-CFD软件原理与应用[M].北京：清华大学出版社，2002.

[5] ANDERSON J D.Computation Fluid Dynamics[M].北京：清华大学出版社，2002.

[6] 赵洪章.基于Fluent的导弹气动特性计算[J].弹箭与制导学报，2006， 27(2)：204.

[7] 谢志敏.卷弧尾翼火箭弹侧向气动特性数值计算[J].空气动力学学报，2010， 28(1)：66.

[8] 秦豪.基于Fluent的弹道修正弹制导状态气动仿真[J].四川兵工学报，2010， 31(7)：31.

[9] 张枫.基于Fluent软件包的制导炮弹气动力参数计算技术研究[D].南京：南京理工大学，2010.

[10] 苗瑞生.导弹空气动力学[M].北京：国防工业出版社，2008.