某异形弹丸的气动特性研究

2018-05-08黄银柳陶如意陈燕婷

兵器装备工程学报 2018年4期

黄银柳,陶如意,王骁,陈燕婷

(南京理工大学能源与动力工程学院，南京 210094)

对于各种炮弹、航弹、火箭弹和导弹，若配制子母战斗部，将能构成大纵深突击和大面积压制火力，能够有效地阻击敌人的坦克、装甲车等重要军事目标[1]。2009年至今，伴随着科技的不断进步发展，计算机技术的不断提高，数值模拟技术越来越受到广大科研工作者的青睐[2-6]。在CFD软件出现之前，常采用风洞实验计算空气动力，其边界效应、支架干扰无法满足相似准则等缺点无法避免。Fluent软件的应用和发展，使空气动力的计算变得越发便捷与准确，克服了风洞实验的不足之处。Fluent模拟从不可压缩到高度可压缩范围内的复杂流动，由于采用多重网格加速收敛技术和求解，可得到最佳的求解精度和收敛速度[7]。

但是，在相关的飞行物气动特性计算中，其所涉及的结构多为常见的圆柱状，当弹体飞行时，整个弹体的受力较为均匀。本文所述则是较为少见的纵截面为近梯形的子弹弹体。后部为4片长方形翼型尾翼。子弹从母弹壳体分离后，尾翼会展开到预设的角度，子弹弹体及尾翼两端呈轴对称。弹体形状的变化对气动特性产生很大的影响，升力、阻力、俯仰力矩等都会随之改变。本文针对某异形弹丸飞行时的气动特性问题，利用FLUENT软件对纵截面为近梯形的弹丸进行定常数值仿真计算，通过建立异形弹体的几何模型、网格划分、FLUENT中的相关参数进行设置并迭代计算，得到弹丸在不同攻角和马赫数下的升力系数、阻力系数、俯仰力矩系数，为进一步研究异形弹体的气动特性和弹道特性提供了理论依据。

1 弹丸的物理模型与网格划分

用ANSYS软件包中的前置处理器ICEM，按照由点到线，由线到面，由面到体的原则对弹体进行建模。几何模型纵剖面为近梯形，尾翼采用四翼式布局，翼型为长方形。弹体特征长度1 000 mm，最大直径115 mm，最小直径35 mm。为减小风阻，头部小圆柱体结合处采用倒角。弹体左右对称，采用一半进行计算。计算模型如图1所示。根据尺寸比例在弹体外围设置一个绕流流场：外围计算域采用长度为8倍弹长、宽度为5倍弹长，高度为3倍弹长的立体域。设置6层弹体棱柱边界层，并在机翼附近加密。网格划分如图2所示。

2 计算模型

Fluent软件包含丰富的物理模型，例如相变模型、辐射模型、离散相变模型、多相流模型、化学组分输运和反应流模型、计算流体流动和热传导模型(其中包括层流、湍流、定常与非定常流动、自然对流、不可压缩与可压缩流动、周期流、旋转流、时间相关流动等)。针对需要解决的物理问题流动特点，软件中都有较为适合的数值解法。选择显式或隐式差分格式，可以在整体稳定性、计算精度与速度等方面达到最佳效果。

可用的湍流模型各有其优点与缺点。雷诺应力模型可以较好的处理各向异性较强的湍流流动，但不适合于一般的回流流动，且其计算量巨大，结构复杂。方程如下[8-9]：

Dij+φij+Gij-εij

(1)

其中：Dij为扩散项；φij为压力应变项；Gij为产生项；εij为耗散项。

大涡模拟适用于各种高雷诺数流动，其对网格的质量要求极为严格。N-S方程为

(2)

修正N-S方程为

(3)

其中

(4)

k-ε湍流模型则是最广泛应用的一种湍流模型，能够比较精确地预测平面和圆形射流的散步率。其中，湍流动能方程为

Gk+Gb-ρε-YM+SK

(5)

扩散方程为

(6)

湍流模型采用单方程Spalart-Allmaras模型。其优点是只需要求解湍流黏性运输方程，剪切层厚度则不用计算，鲁棒性好，不需要精确的网格划分且计算量不大，较适用于此类空气流动问题。其方程为

(7)

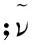
3 计算求解

1) 以ICEM对弹丸的相关区域划分网格并优化，检查网格质量，无误后输出网格文件。

2) 将网格文件导入FLUENT中，检查最小网格尺寸是否大于0。使用基于密度耦合求解器，选择上述单方程湍流模型。

3) 选择气体黏度满足萨兰德定理的物理属性设置，以理想气体做介质。

4) 壁面边界条件：无滑移。

5) 差分格式选择：动量、湍流动能以及湍流耗散率均选用二阶迎风格式；压力差值设为默认。

6) 边界条件设置大气压为101 325 Pa，马赫数与攻角数见下文所述。

7) 设置松弛因子：压力项设为0.7，密度与质量设为1，动量项设为0.6，湍动能项、湍流黏性项与耗散率项均设为0.5。

8) 定义对称面为SYMMERY，其余计算域边界条件设为PRESSURE-FAR-FIELD。

9) 定义监视器，进行6 000步的迭代计算[10-13]。

4 气动特性计算结果与分析

初始阶段，在给定的攻角和来流马赫数下，升力系数、阻力系数和俯仰力矩系数随着迭代次数的不断增加而产生震荡。一直到迭代次数超过2 500步后，波动明显减弱，曲线趋于平稳，就可以在图中读出升力系数、阻力系数、俯仰力矩系数等相关参数的数值。图3是升力系数随迭代过程变化曲线，图4是阻力系数随迭代过程变化曲线，图5是俯仰力矩系数随迭代过程变化曲线。可以看出，弹体气动特性收敛，表明系统的设计较为稳定。从图6可得，弹头和翼梢前端所受压强最大。

4.1 升力特性分析

在0°、3°、6°、9°、12°攻角下，进行不同马赫数下的仿真实验，得到升力系数变化曲线(图7)如下：

从图7可以看出，在相同的攻角条件下，由于来流马赫数不同，升力系数由大到小的顺序为0.6Ma、0.5Ma、0.4Ma，即弹丸的升力系数随着来流马赫数的增加而增大。对于攻角来说，在来流马赫数相同的情况下，升力系数随着攻角的增加而增大。攻角在0°～ 6°时，升力系数与攻角成准线性关系；在6°～9°时，升力系数极速上升；超过9°后，升力系数曲线又回归平缓，升力系数随攻角增加而增大的趋势减小。

4.2 阻力特性分析

在0°、3°、6°、9°、12°攻角下，进行不同马赫数的仿真实验，得到阻力系数变化曲线如图8。

从图8可以看出，在相同的攻角条件下，由于来流马赫数不同，阻力系数由大到小的顺序为0.6Ma、0.5Ma、0.4Ma，即弹丸的阻力系数随着来流马赫数的增加而增大，且系数增加的幅度大致相同。对于攻角来说，在来流马赫数相同的情况下，阻力系数随着攻角的增加而增大，攻角在0°～ 12°时，阻力系数与攻角成准线性关系，只是在攻角超过9°时，阻力系数随攻角增加而增大的趋势稍微增大。