车辆-轨道系统激振源随机分析

徐 磊，陈宪麦

(1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.中南大学 土木工程学院，湖南 长沙 410075)

对于车辆-轨道耦合系统(本文简称此系统)而言，随着确定性计算理论的不断完善[1]，车线工况及激励形态确定的系统振动分析不再是困扰铁路工作者的主要问题。此系统本质上是随机动力系统，激振源的随机性是其随机振动的重要原因，国内外对此系统的随机振动研究尚不充分。一般将随机激振源取为轨道随机不平顺[1]，文献[2]另辟蹊径，取构架蛇形波为此系统的横向激振源。

总结国内外关于此系统激振源随机分析的研究，以下几个问题有待深入探讨：

(1)激振源时变性考虑不足。按功率谱(或能量)等效原理反演的轨道随机不平顺或构架蛇形波样本，均来自此系统某一概率水平或某一时间点下的实测谱(或标准差)，其动力计算结果实为此系统沿线路的空间随机结果[2-3]。

(2)激振源的时-空随机模拟方法尚未提出。此系统的激振源既有沿线路空间的分布随机性，又有随时间的演变随机性，所以此系统的激振源具有时-空随机特征。若不进行此系统的时-空随机计算，就无法统计振动响应的概率分布，则涉及此系统可靠度的问题均无法妥善解决。

(3)自文献[2]提出采用构架蛇形波作为此系统横向激振源，已近30年。未见针对此激振源合理性进行全概率的理论论证，并与车辆-轨道耦合动力学[1]计算结果进行对比验证的相关文献。

本文以轨道随机不平顺的时-空随机性为基础，阐述其随机反演方法；结合车辆-轨道耦合动力学模型[1]，分析时-空随机不平顺输入下此系统构架蛇形波的随机分布特性及模拟方法；进一步建立车辆-轨道动力计算模型，以构架蛇形波谱的随机反演样本为激振源，通过两种激振源在两种计算模型下的动力响应，相互验证此系统两种激振源的概率转换关系及合理性。

1 轨道随机不平顺时-空随机反演方法

轨道不平顺的空间随机表现为其幅值及相位沿线路随机分布(一般通过功率谱表征)，其时间随机表现为谱线以不同的概率上、下波动。

图1为武广高速铁路2013年高低不平顺实测谱分布。图1表明，时-空域内的随机谱线在较广的范围内波动，极大极小谱值相差超过3个数量级。而国内外经常使用的平均谱，仅是众多统计谱线中的一条，其出现概率及激励形态均十分有限，将平均谱作为激振源计算出的响应并不完备。只有从此汇总谱图中还原出线路随机不平顺的所有激振形态及其出现概率，才能计算出此系统的所有振动响应(包括最不利极值响应)及其概率分布，并开展可靠性研究。

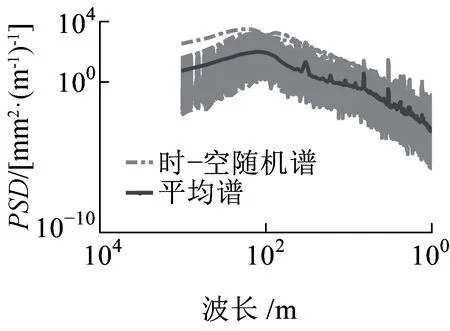
图1 轨道高低不平顺实测谱

1.1 轨道不平顺谱的概率特征

轨道不平顺的时-空随机反演重在遍历轨道随机不平顺所有激振形态，并赋予其概率性质。计算表明，图1中的所有谱线均对应确定的概率水平，即在某一确定时-空随机域内，不同波长的谱密度值与其出现概率一一对应。

文献[4]研究表明，当取样足够长时，对于任何一个分布函数F(x)，上极限分布H(x)必收敛为与原始分布有关的3种形式，并可统一为广义极值分布[5]，其分布函数为

( 1 )

式中：μ，σ分别为位置参数和尺度参数；ξ为形状参数；I(x)为示性函数，即

( 2 )

当ξ=0时，式( 1 )为Gumbel分布，即极值Ⅰ型；当ξ>0时，式( 1 )为Frechet分布，即极值Ⅱ型；当ξ<0时，为Weibull分布，即极值Ⅲ型。计算得到式( 1 )的参数后，可根据给定的概率水平H′求解对应的逆函数

( 3 )

文献[6-7]采用参数估计及假设检验方法，计算获得不同类型不平顺不同波长谱值的概率分布参数(μ、σ和ξ值)，并验证了线路不平顺谱服从广义极值分布。图2为实测90百分位数谱与广义极值分布90百分位数谱的比较图。

图2 90百分位实测谱与广义极值分布转化谱比较

从图2可知，线路实测谱与概率分布拟合谱能较好吻合，证明了用广义极值分布进行轨道随机不平顺概率分析是可行的。

1.2 基于谱密度的随机反演方法

令轨道不平顺谱密度值为波长和概率水平(用百分位数表示)的函数，即

PSD(ζ,λ)={Pζi,λj|ζi=ζl～ζu；λj=λl～λu}

( 4 )

式中：P为谱密度值；ζi为波长，ζu、ζl分别为上、下限截止波长；λj为百分位数，λu、λl为上、下限截止百分位数。

式( 4 )包含了不同频率、不同概率下的谱密度值，而单边功率谱密度序列G(ω)与轨道不平顺反演值之间存在下列关系

( 5 )

从式( 5 )可知，轨道不平顺反演值与功率谱密度值存在概率信息的转换关系，在频率与百分位数确定的情况下，G(ω)的概率密度是可以确定的。

( 6 )

式中：Pr(·)表示概率密度。

采用谐和函数[8]模拟轨道不平顺

( 7 )

从式( 7 )可知，每条随机不平顺序列X(t)的出现概率可由Ai的概率决定，基于式( 6 )，可得

( 8 )

可进一步假定线路谱线均按百分位谱形式排列，形成百分位谱密度矩阵

( 9 )

式( 9 )中矩阵的每一列满足如下关系

(10)

即每个频率与其对应谱密度值序列构成独立的概率子集，在这里若考虑线路谱线的百分位形式，则其不再独立，可进一步将不同不平顺类型的百分位概率密度矩阵构建为一个二维联合概率密度集，即

(11)

可以获得任意百分位谱G(λi)的出现概率为

(12)

由G(λi)反演获得的轨道随机不平顺序列Xλi(t)具有与G(λi)相等的出现概率，这便完成了具有概率特征的随机不平顺反演工作。

根据不同百分位谱线出现的概率，通过超立方抽样方法[9]随机提取m个谱线样本，统计m个样本轨道不平顺幅值的概率密度分布，即获得每个不平顺幅值在整个线路中出现的近似概率。通过试算，可取m范围为300～500。图3为m=300时，不平顺幅值反演概率密度分布与实测概率密度分布的比较；图4为不同累计概率下谱线的概率分布。

图3 高低不平顺反演概率分布与实测概率分布的比较

图4 不同累计概率下谱线的概率分布

由图3可知，反演获得的概率密度分布与实测十分接近，证明本文提出的具有概率特征的随机不平顺反演方法是可行的。由图4可知，概率水平最高的轨道不平顺谱线出现在较低百分位数下，此概率分布曲线与广义极值分布较相似。

其他类型的不平顺均可参照上述方法进行时-空随机模拟。对于不同类型不平顺样本的组合问题，文献[10]基于华罗庚和王元分圆域思想，提出一种随机变量空间选点的数论方法，可供参考，这里不再赘述。

2 构架蛇形波谱计算与统计

将上述轨道不平顺随机样本输入经过验证的车辆-轨道耦合动力学模型[1]，进行轨道随机不平顺激振下此系统振动响应的计算。结果表明，计算获得的构架横向振动加速度谱仍然可用广义极值分布进行概率分析，如图5所示。

图5 构架横向蛇形波计算谱和转换谱比较注：1、2、3、4分别表示10、30、70、90百分位数谱。

从图5可知，采用广义极值分布能良好拟合构架横向蛇形波在不同累计概率水平下的功率谱线。振动主频主要分布在14～42 Hz范围内，且存在34 Hz及其倍频谱峰，这些计算结果与文献[1]中给出的实测结果吻合良好。

根据构架蛇形波谱，可以依据功率谱等效算法[1]模拟构架加速度响应，采用基于卡尔曼滤波的状态空间方法[11]估计其位移响应，对位移关于时间一次差分计算对应的速度响应。计算结果表明，此方法效果良好，不会产生时域积分时的漂移现象，如图6所示。

图6 模拟速度时程与计算速度时程对比

从图6可知，按上述模拟思路，模拟结果与实际计算结果较一致，模拟方法可行。

图7为99百分位数构架蛇形波谱的振动响应模拟时程。

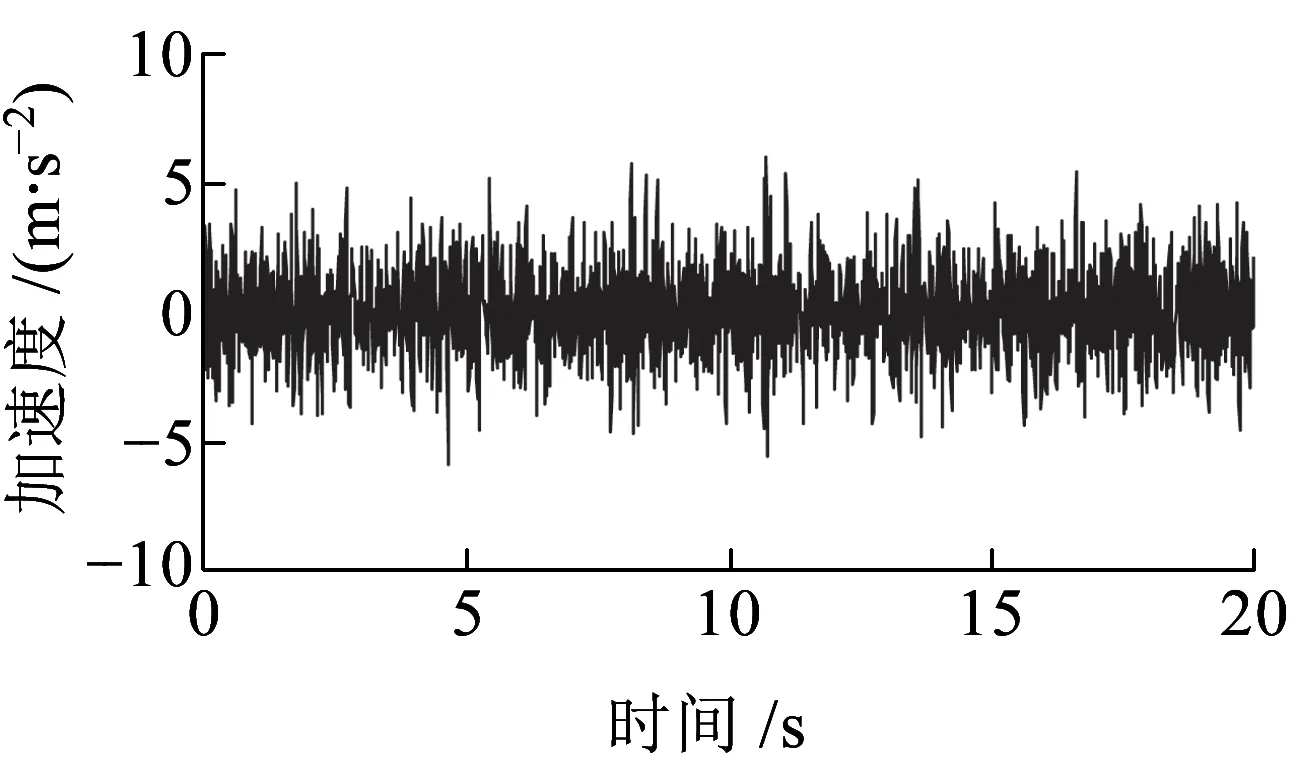
(a)构架横向加速度

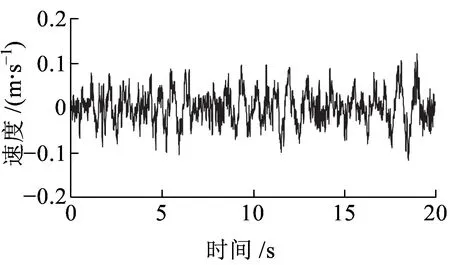
(b)构架横向速度

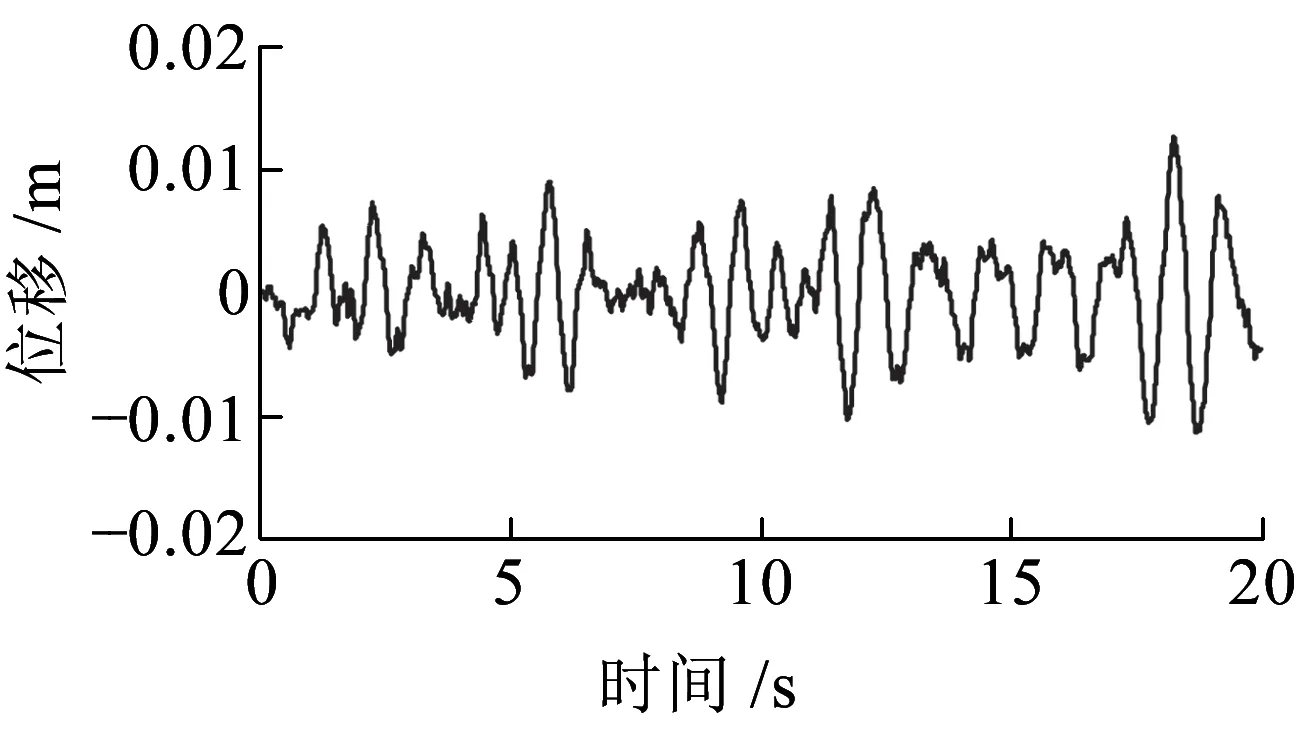
(c)构架横向位移图7 构架蛇形波99百分位数谱的振动响应模拟时程

将图7所示模拟结果与实际动力计算结果最大值进行比较，发现此模拟值与计算值基本吻合，如模拟和计算位移最大值分别为0.012 7和0.012 4 m。

3 动力计算模型

3.1 模型简介

以轨道不平顺为激振源的车辆-轨道耦合动力学模型在文献[1]中有详细介绍，不再论述。本文介绍以轨道垂向不平顺和构架横向蛇形波为此系统垂、横向激振源的车辆-轨道动力计算模型。

不考虑风、地震等外部激励，此系统是自激系统，其空间振动方程为

(13)

基于弹性系统动力学总势能不变值原理[12]和形成矩阵的“对号入座”法则[2]，将此系统视为一个整体系统，轮轨界面不是此系统的边界条件，而是作为系统的内部环境考虑。除车辆自重外，此系统荷载列阵来自振动参数的已知响应，轮轨相互作用力已等效计入系统能量位移变分后的动力矩阵之中，无需显式计算。

无论采用何种动力计算模型，轮轨接触几何关系均无法回避。根据文献[13-14]，在本文计算模型中考虑车轮爬轨和跳轨，将轮轨位移衔接条件(轮轨位移=钢轨位移+轨道不平顺+轮轨相对位移)作为轮轨接触几何关系的基本条件。在计算中，轮轨相对位移通过能量变分导入系统动力矩阵之中，无需计算。

采用文献[15]的车辆模型，但考虑轮对的摇头振动。采用文献[16]的板式轨道结构模型。用Wilson-θ法求解式(13)，积分步长为0.005 s。

3.2 模型验证

本文将动力计算模型的验证分成两个部分：

(1)与车辆-轨道耦合动力学模型[1]的计算结果进行对比。

(2)基于列车脱轨能量随机分析理论[17]，计算车辆-板式轨道系统的极限抗力做功值，与文献[16]的计算结果进行对比。

3.2.1 验证一

采用相同的计算条件，以高速无砟轨道谱90百分位数谱为车辆-轨道耦合动力学模型[1]的激励输入，计算此系统振动响应(包括构架蛇形波)。将构架蛇形波及轨道随机不平顺输入本文模型，再次计算此系统的振动响应，表1为计算响应最大值的对比。

表1 计算响应最大值对比

由表1可知，对于各项动力指标的计算最大响应，本文所构建的动力计算模型与车辆-轨道耦合动力学模型的计算结果基本接近，从而验证了本文计算模型的可靠性，也侧面验证了不同激振源在不同动力模型中相互转换计算的可行性。

3.2.2 验证二

根据列车脱轨能量随机分析方法[16]，取车轮抬升量27 mm为脱轨几何限值。采用试算法，计算出此系统时速350 km的脱轨极限抗力做功σc=6.12 m/s2，略高于文献[16]的计算结果，因为本文所取的车轮抬升量限值大于文献[16]的25 mm。图8为部分指标的脱轨计算时程。

由图8可知，轮对爬轨一般伴随较强烈的车轮减载现象(图8(c))，由此车辆系统横向摇摆剧烈、车辆系统侧向倾覆所致；同时，车轮脱轨必然伴随轮缘撞击钢轨，引发轮轨撞击，对于不同侧轮轨，此轮缘撞击力方向相反；在轮轨反复撞击过程中，单侧轮对的脱轨系数一般呈现非对称性(图8(d))。

(a)车体横向加速度

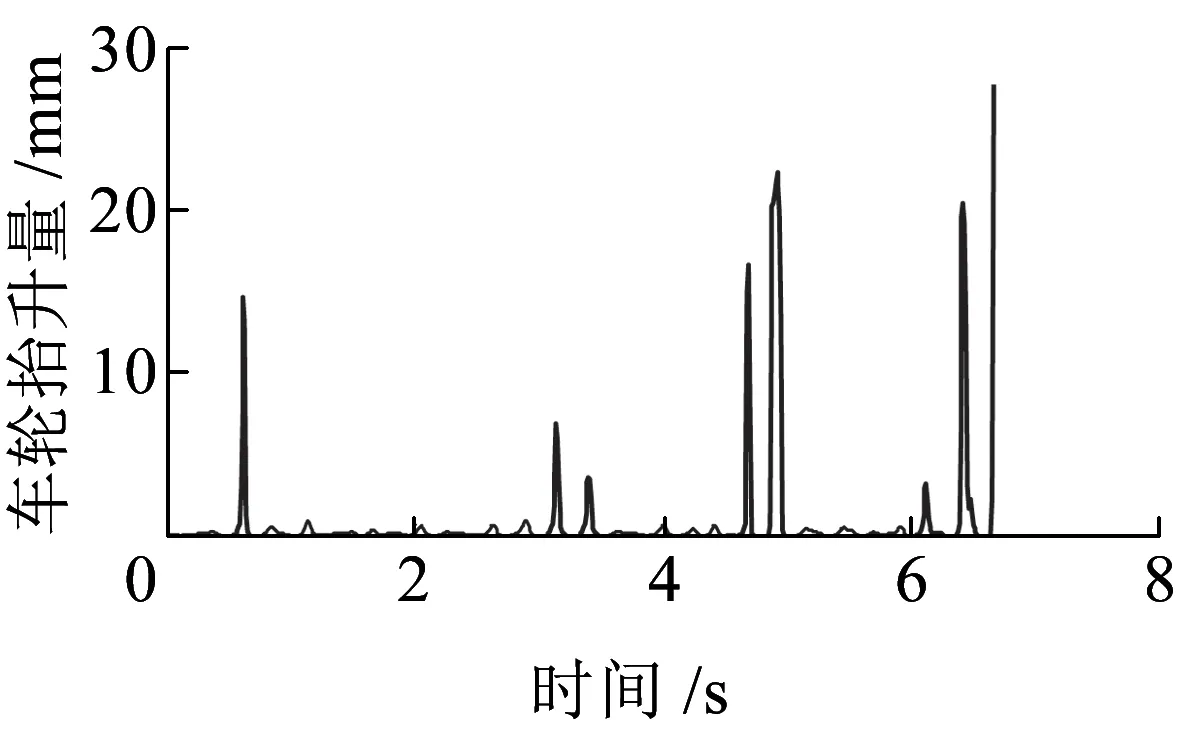
(b)第四轮对左轮抬升量

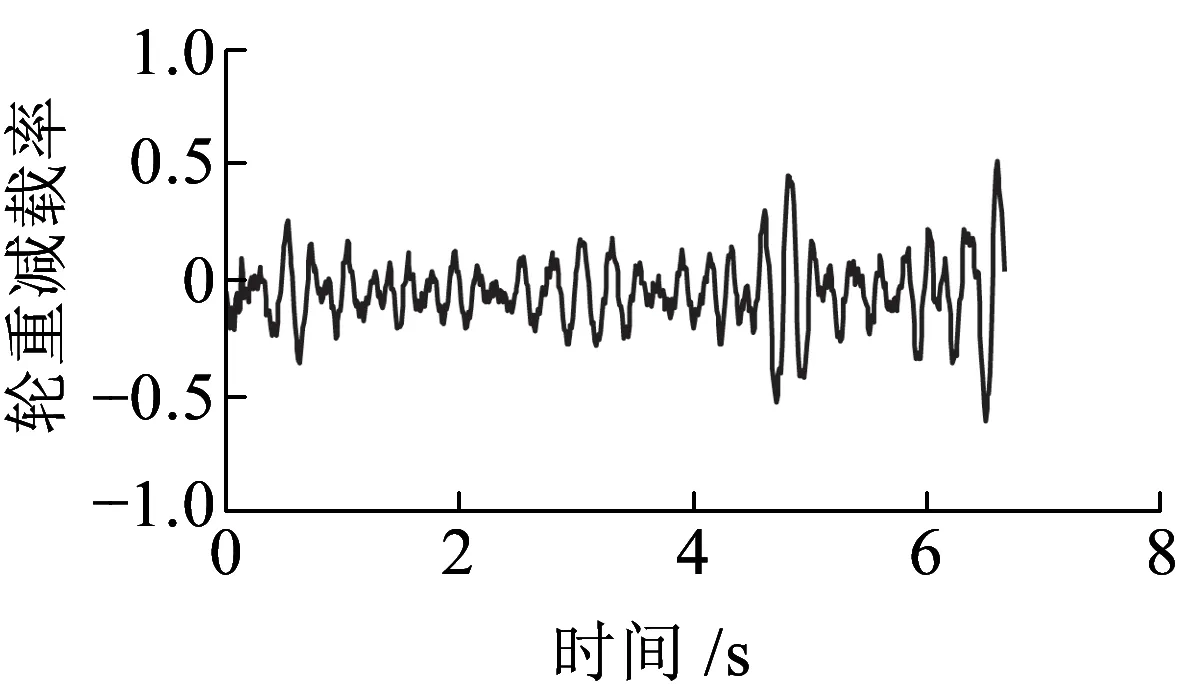
(c)第四轮对左轮轮重减载率

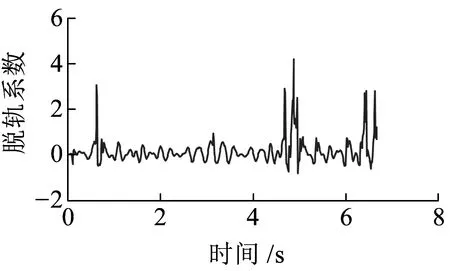
(d)第四轮对左轮脱轨系数图8 车辆脱轨动力指标计算时程曲线

4 激振源的对比验证

本文开展激振源的时-空随机分析工作，重新审视将构架蛇形波作为系统激振源的合理性，目的在于细化激振源的随机振动分析，对不同激振源在动力分析中的作用展开细致研究。在以上工作基础上，可以通过两种激励源下的系统动力响应概率极值分布进行两种激振源可行性对比验证。计算流程如下：

(1)以本文反演出的轨道不平顺时-空随机样本(第1章)为激励输入，采用车辆-轨道耦合动力学模型[1]计算动力响应指标在不同累计概率下的振动响应极值。

(2)提取不同累计概率下的构架蛇形波百分位数谱，模拟出对应的振动响应时程(第2章)，此为横向激振源；垂向激励则取轨道垂向不平顺百分位数谱。采用本文建立的动力模型(第3章)，再次计算动力响应指标在不同累计概率下的振动响应极值。

(3)将(1)和(2)中计算响应的累计概率-响应极值分布对比验证。

篇幅所限，仅给出车体横向加速度、轮轨横向力及钢轨横向位移的极值分布对比，如图9～图11所示。

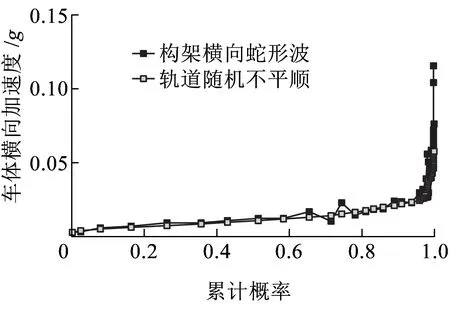
图9 车体横向加速度累计概率-响应极值分布

图10 钢轨横向位移累计概率-响应极值分布

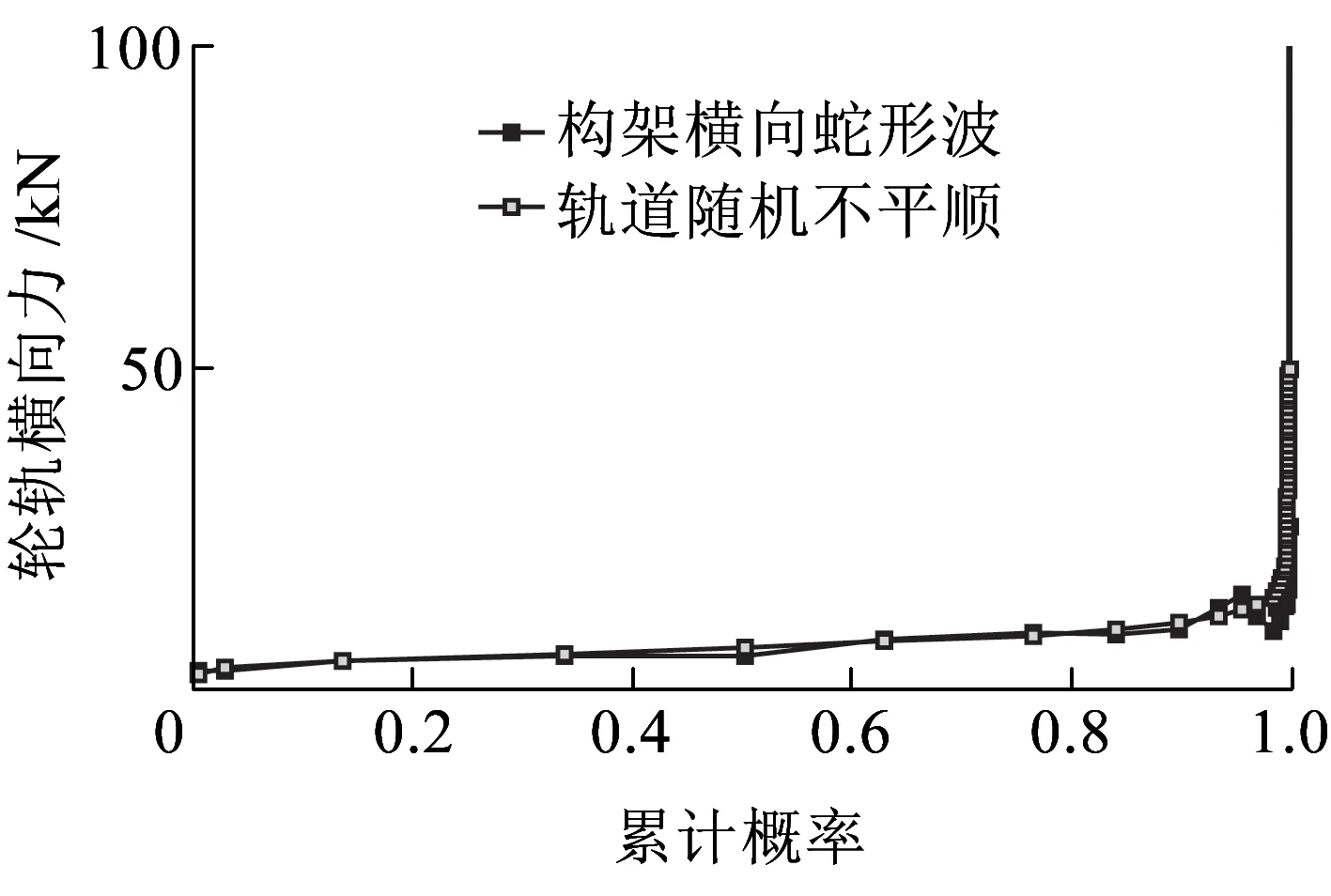
图11 轮轨横向力累计概率-响应极值分布

由图9～图11可知，通过构建不同的动力计算模型，发现在不同的概率水平下，两种激振源下此系统理论计算结果较吻合。此吻合是指此系统响应的全概率吻合，该计算结果说明：

(1)此系统激振源与其振动响应之间存在概率转换关系，例如轨道随机不平顺与构架蛇形响应存在的概率转换关系，此关系可通过车辆-轨道耦合动力学[1]理论计算和统计分析获得。

(2)将构架蛇形波作为横向激振源计算系统最大响应是可行的，图9～图11的计算结果证明了这一点。关键是用于动力计算的理论模型是否合理描述了该系统的物理、力学关系。

5 结论

(1)简述轨道不平顺的时-空随机特性，并给出了相应的时-空随机模拟方法。以往的研究多对线路的单一统计谱线进行动力计算与分析，未考虑线路谱随时间和空间的随机波动性。随着铁路大系统动力学非确定性计算工作的不断深入，应该深入考察此随机性，为时-空随机激振下的车辆-轨道系统动力演化特性分析奠定基础。

(2)本文较多从理论层面探讨轨道随机不平顺时-空随机样本的概率计算及反演方法。大量基础检测数据和资料积累、此系统基础部件性能演化规律及完善的车辆-轨道耦合动力模型等研究工作的展开，是此方法应用于工程实际的关键。

(3)不同计算理论的对比证实了将构架蛇形波作为激振源具有合理性。实际上，若将系统动力学的基本思想拓展至车辆-轨道耦合系统之中，即系统内部各组成要素的动力反应不是独立的，而是具有互为因果的反馈特性，便不难理解其合理性。若研究者掌握了与此激振源相符的动力模型构造原理及方法，便能获得与实际吻合的计算结果。

(4)采用激振源时-空随机分析方法，利用车辆-轨道动力计算模型，可以计算出不同动力指标在不同概率水平下的响应，为此系统可靠性计算奠定了基础。

参考文献：

[1]翟婉明.车辆-轨道耦合动力学[M]. 4版. 北京：科学出版社，2015.

[2]曾庆元，郭向荣. 列车桥梁时变系统振动分析理论与应用[M].北京：中国铁道出版社，1999.

[3]陈果，翟婉明，左洪福. 车辆-轨道耦合系统随机振动响应特性分析[J]. 交通运输工程学报，2001，1(1)：13-16.

CHEN Guo, ZHAI Wanming, ZUO Hongfu. Analysis of the Random Vibration Responses Characteristics of the Vehicle-track Coupling System [J]. Journal of Traffic and Transportation Engineering, 2001, 1(1):13-16.

[4]FISHER R A, TIPPETT L H C. Limiting Forms of the Frequency Distribution of the Largest or Smallest Members of a Sample[J]. Mathematical Procceedings of the Cambridge Philosophical Society, 1928, 24(2): 186-193.

[5]COLES S. An Introduction to Statistical Modeling of Extreme Values [M]. New York: Springer Verlag, 2001: 36-78.

[6]杨谋存，聂宏.三参数Weibull分布参数的极大似然估计数值解法[J].南京航空航天大学学报，2007，39(1)：22-25.

YANG Moucun, NIE Hong. Advanced Algorithm for Maximum Likelihood Estimation of Three Parameter Weibull Distribution [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(1): 22-25.

[7]王梓坤.概率论基础及其应用[M]. 3版. 北京：北京师范大学出版社，2007：283-284.

[8]陈建兵，李杰.随机过程的随机谐和函数表达[J].力学学报，2011，43(3)：505-513.

CHEN Jianbing, LI Jie. Stochastic Harmonic Function and Spectral Representations [J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 505-513.

[9]MCKAY M D, BECKMAN R J, CONOVER W J. Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code [J]. Technometrics, 1979, 21(2): 239-245.

[10]陈建兵，李杰.结构随机响应概率密度演化分析的数论选点法[J].力学学报，2006，38(1)：134-140.

CHEN Jianbing, LI Jie. Strategy of Selecting Points via Number Theoretical Method in Probability Density Evolution Analysis of Stochastic Response of Structures [J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 134-140.

[11]LEE J S, CHOI S, KIM S S, et al. Waveband Analysis of Track Irregularities in High-speed Railway from On-board Acceleration Measurement [J]. Journal of Solid Mechanics and Materials Engineering, 2012, 6(6): 750-759.

[12]ZENG Q Y, LOU P, XIANG J. The Principle of Total Potential Energy with Stationary Value in Elastic System Dynamics and Its Application to the Analysis of Vibration and Dynamic Stability [J]. Journal of Huazhong University of Science & Technology:Urban Science Edition, 2002, 19(1): 7-15.

[13]陈果，翟婉明，左洪福.新型轮轨空间动态耦合模型[J].

振动工程学报，2001，14(4):23-29.

CHEN Guo, ZHAI Wanming, ZUO Hongfu. The New Wheel/rail 3-dimensionally Dynamically Coupling Model [J]. Journal of Vibration Engineering, 2001, 14(4):23-29.

[14]向俊，曾庆元. 直线货物列车脱轨过程计算[J]. 铁道学报，2002，24(2)：104-108.

XIANG Jun, ZENG Qingyuan. Simulation of the Derailment Courses of Freight Train on Tangent Track [J]. Journal of the China Railway Society, 2002, 24(2): 104-108.

[15]李德建，曾庆元.列车-直线轨道空间耦合时变系统振动分析[J]. 铁道学报，1997，19(1)：101-107.

LI Dejian, ZENG Qingyuan. Dynamic Analysis of Train-tangent-track Space-coupling Time-varying System[J]. Journal of the China Railway Society, 1997, 19(1): 101-107.

[16]赫丹. 客运专线无碴轨道高速列车走行安全性分析理论与应用研究[D]. 长沙：中南大学，2009:7.

[17]曾庆元，向俊，周智辉，等.列车脱轨分析理论与应用[M]. 长沙：中南大学出版社，1970.