风电机组电动变桨系统载荷计算分析与数据驱动控制建模

文 | 王洪印，张中磊，薄婷婷

随着世界能源形势日益严峻与新能源发展要求的不断深化，风力发电系统逐步成为各国能源发展及研究者的关注焦点。风电机组的发展历程大致经过：定桨恒速恒频、变桨变速恒频、功率与载荷稳定控制和大规模网络化风电系统等阶段。以目前研发及应用来看，双馈型和直驱型风电机组是最流行、并在未来较长一段时间内具有重大优势的风电系统。风电系统的能量转换为：风能－机械能－电磁能－电能，这种复杂的多形态能量流动关系存在时效性、随机性、非线性、不稳定性等多种特征，而引起风电机组强非线性特征的主要原因在于其所受载荷的随机性与非线性，主要包括气动载荷控制和多体结构动力学的耦合。

变桨系统连接气动、机电与控制等，是风电机组安全、稳定、高效运行的核心系统。因此，对变桨系统进行载荷计算分析与数据建模是风电机组载荷控制及安全稳定运行的关键。本文从变桨载荷计算与控制的角度出发，首先对电动变桨系统进行载荷计算与载荷分布，提出变桨载荷智能化计算与分析方法，用于变桨系统关键参数计算、运行包络范围确定、载荷校核与控制器反馈设计以及参数相关性分析等；然后结合变桨载荷分布特征，对变桨系统建模问题，提出基于正交最小二乘数据驱动建模方法进行变桨系统阶跃响应的时滞降阶模型参数辨识。

电动变桨系统载荷计算与分析方法

变桨系统控制的实质是通过改变风电机组叶片攻角来控制驱动转矩，即在低风速时保持最佳叶尖速比以实现最大功率跟踪；在高风速时利用风轮转速储存或释放能量，提高传动柔性，实现额定功率稳定控制。从而动态调节风电机组气动载荷，实现气动、机械传动与载荷耦合控制。

一、变桨系统载荷特性与控制耦合

变桨系统载荷计算是风电机组载荷仿真计算的重要部分，直接关系到机组模型稳定性、运行域、部件选型校核以及载荷优化控制策略等。如图1所示，变桨系统载荷连接叶片与风轮气动载荷以及传动系统动力学载荷，同时，变桨系统的动态响应密切影响风电机组转矩－功率等特性，进而影响变桨系统自身的动力学行为，即存在严重的动力学耦合。从变桨系统模型及控制器设计的角度，变桨载荷与控制系统之间也存在设计上的耦合。

变桨系统所承受的载荷包括：气动推力引起的叶片根部倾覆力矩、叶片重力引起的叶片根部倾覆力矩、倾覆力矩引起的叶片轴承摩擦力、叶片重力引起的叶片根部扭矩、气动力引起的叶片根部扭矩等。变桨载荷的气动非线性源于风能利用系数对桨距角和叶尖速比的变化规律具有很强的非线性，如图2所示，由于自然风速、风向变化的随机性，使得变桨工作模态频繁切换，即存在多模态切换控制问题。并且变桨执行机构普遍存在大惯性与时滞饱和非线性等特点，使得变桨系统的载荷计算与数据分析较为复杂。

电动变桨系统在能量与信息拓扑结构上由变桨控制器、变桨驱动、叶片轴承、变桨齿箱、后备电源等组成。如图3与图4所示，Bladed叶根坐标系中坐标原点为叶根与轮毂连接处的中心，沿轮毂－机舱迎风向为X轴，沿叶根－叶尖方向为Z轴，Y轴构成右手坐标系。变桨系统载荷计算可以将叶根坐标系中的载荷分布转换为变桨电机轴侧的载荷信息以及变桨电机的转矩－转速分布特性，进而得到各种载荷工况下的变桨电机运行包络范围及运行边界。

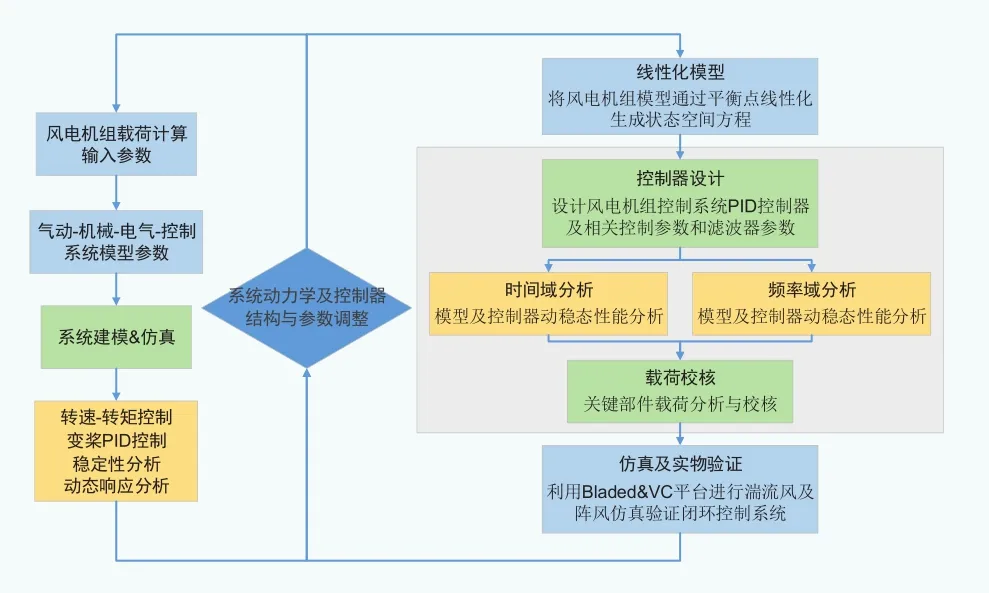
图1 风电机组载荷计算与控制算法设计逻辑图

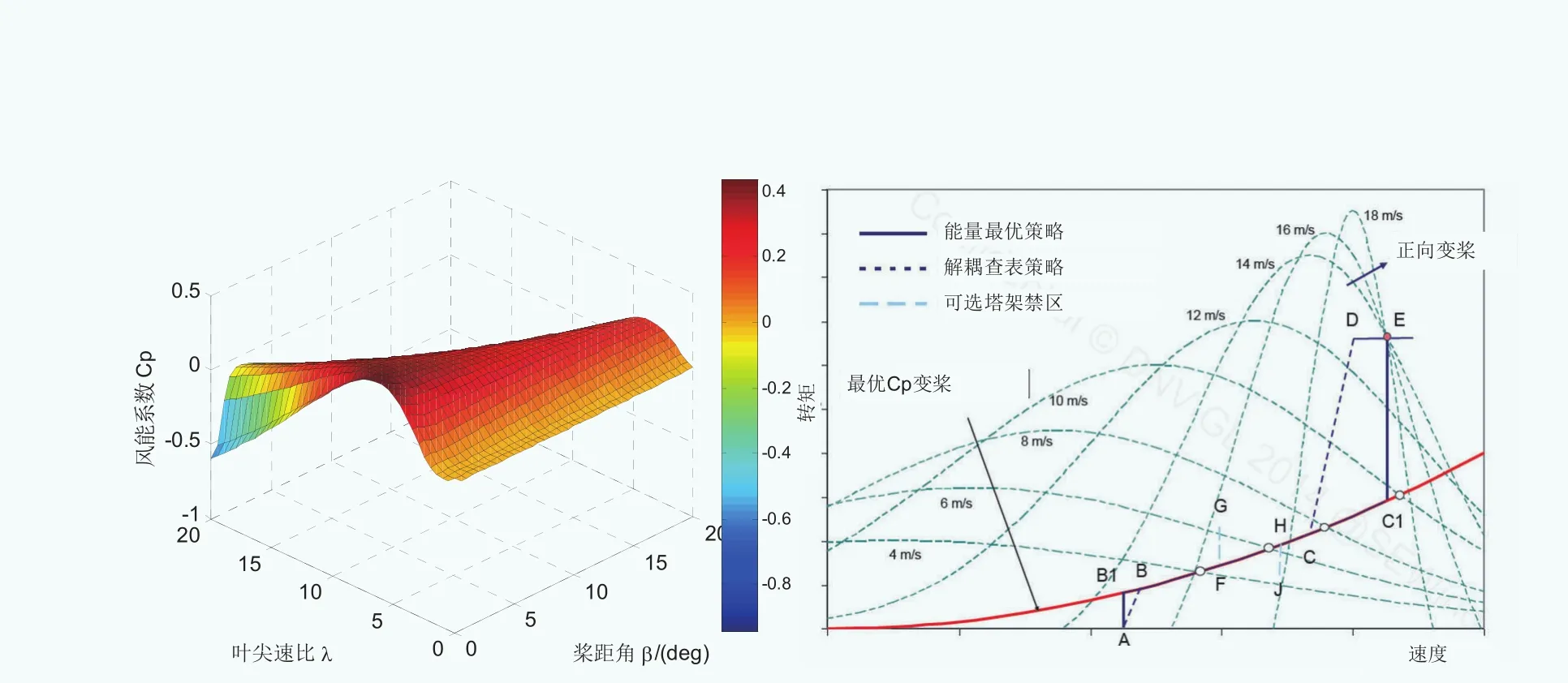
图2 气动非线性与转矩-转速运行模态切换控制

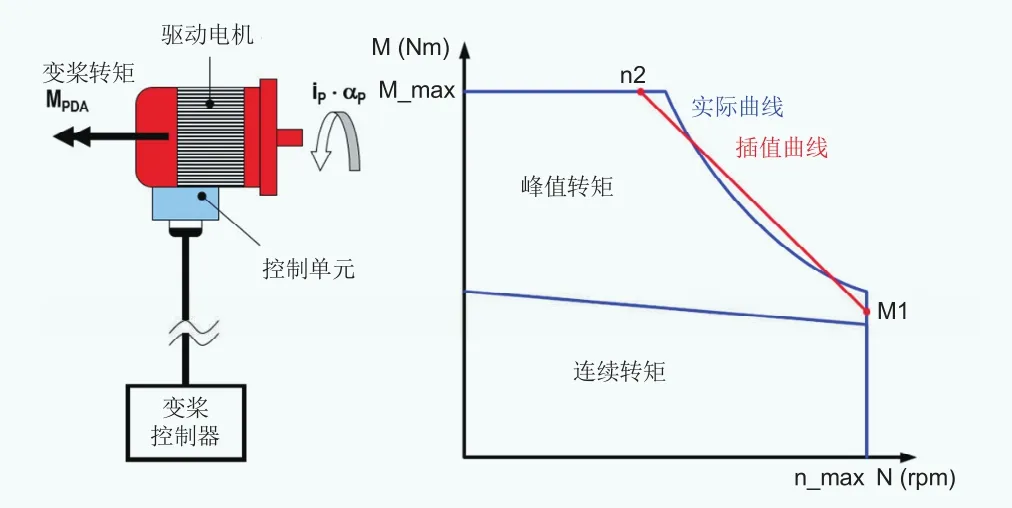
图3 变桨电机转矩-转速机械特性曲线

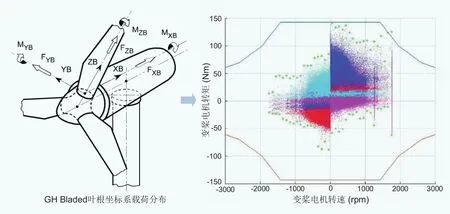
图4 变桨系统叶根载荷分布及变桨电机转矩-转速包络范围

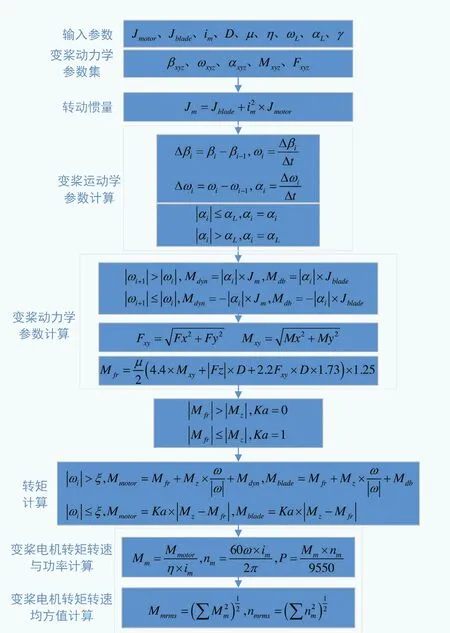
图5 变桨系统载荷计算流程

二、变桨系统载荷计算与分析方法

电动变桨载荷计算算法如图5所示，其中：Jmotor为变桨电机转动惯量，Jblade为叶片转动惯量，Jm为变桨系统总转动惯量，im为叶片侧到变桨电机轴侧变比，D为叶根轴承直径，μ为摩擦系数，η为传动效率，ωL为变桨速度限值，αL为变桨加速度限值，Y为安全系数，β为变桨位置角度，ω为变桨速度，α为变桨加速度，Mxyz为叶根轴承所受力矩，Fxyz为叶根轴承所受力，Mfr为摩擦力矩，Ka为开关系数，Mdyn为总动态力矩，Mdb为叶片轴承动态力矩，Mmotor为转化变桨电机转矩，nmotor为转化变桨电机转速，Mm为变桨电机转矩，nm为变桨电机转速，Mmrms为变桨电机均方根转矩，nmrms为变桨电机均方根转速，P为变桨功率。

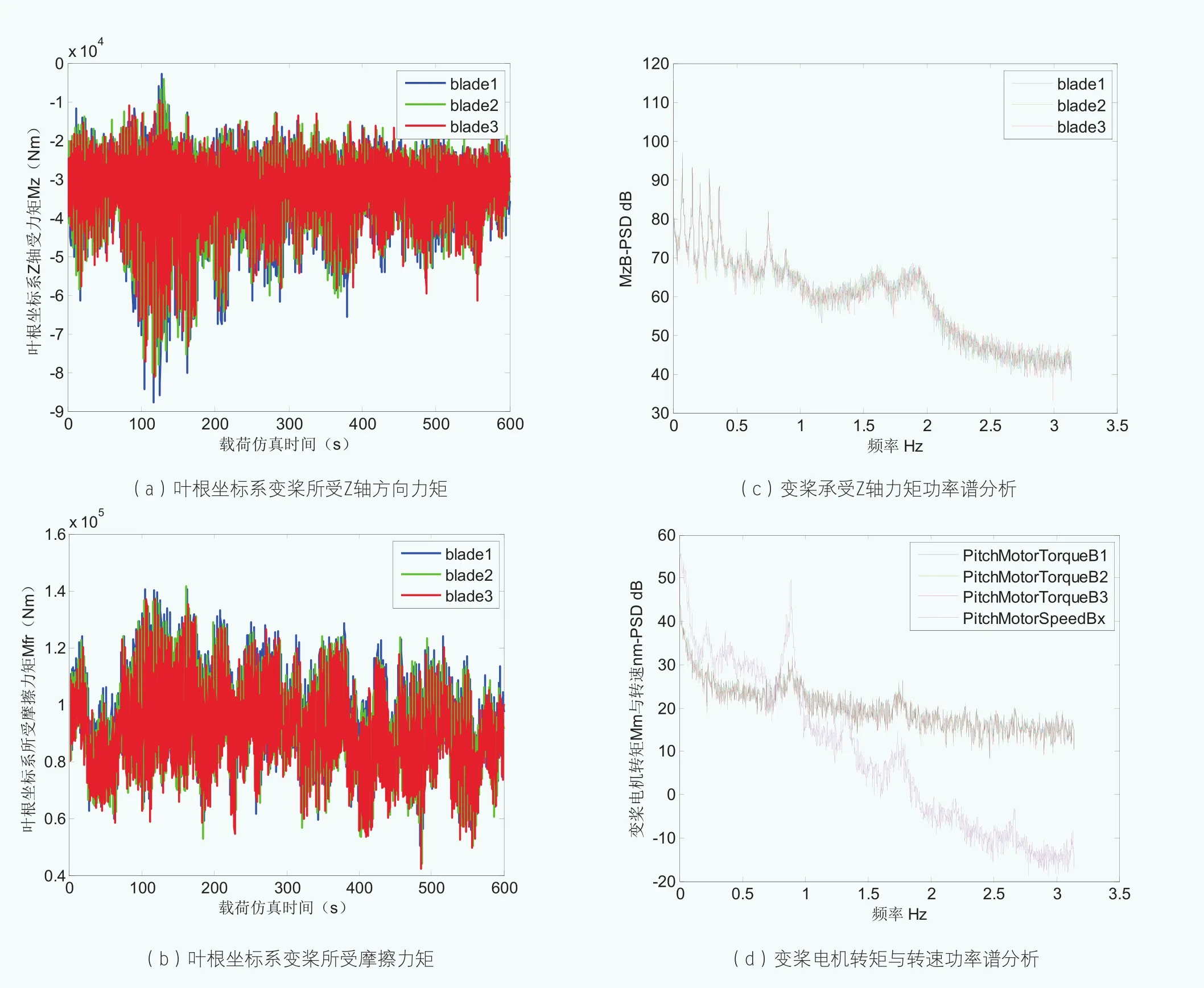
图6 DLC1.2工况变桨载荷计算

根据风电机组载荷仿真计算文件和规范IEC61400-1，以某机型变桨载荷计算为例，分析变桨系统在仿真工况DLC1.2和DLC2.3下的载荷分布及变桨电机转矩－转速包络范围。其中，DLC1.2为疲劳载荷工况，DLC2.3为极限载荷工况。变桨载荷智能化计算结果分析如下：

（一）DLC1.2正常发电疲劳载荷工况

图6所示（a）、（b）分别为变桨轴承Z轴扭转载荷力矩及摩擦力矩，三轴载荷保持平衡，表现出较强的非线性振动，（c）为Z轴力矩的功率谱密度分布，（d）为变桨电机侧的转矩及转速功率谱密度分布，在0.5Hz～1Hz及1.5Hz～2Hz范围内载荷功率分布较集中，表明在该频率范围内变桨系统承受的载荷分布明显。

图7所示为疲劳工况变桨载荷转化为变桨电机转矩－转速的分布范围，可以看出，变桨电机的运行点集中在第I、III、IV象限，并且在电机正向转速即正向变桨过程中，转速基本在600rpm以内，转矩在±50Nm范围内，而反向转速包络在500rpm以内，转矩值在150Nm范围内，此时变桨电机承受峰值转矩工况。同时，根据分布特征看到，3个变桨轴电机承受的载荷表现出不平衡特征。

（二）DLC2.3正常发电极限载荷工况

图8所示（a）、（b）分别为变桨轴承Z轴扭转载荷力矩及摩擦力矩，三轴极限载荷表现出不平衡特征，非线性振动较为剧烈，（c）为Z轴力矩的功率谱密度分布，在1.7Hz～2.2Hz范围内载荷功率分布较集中，（d）为载荷转换到变桨电机侧的转矩及转速功率谱密度分布，在整个频率范围内较为平稳，即单轴所承受载荷比较稳定。

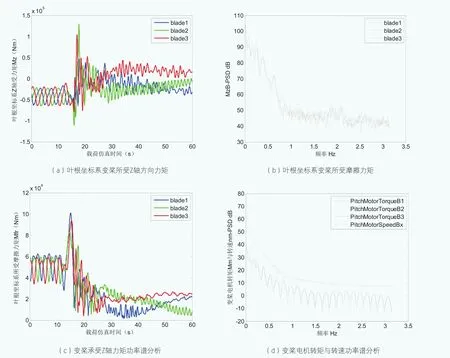
图8 DLC2.3工况变桨载荷计算

图9所示为极限工况变桨载荷转化为变桨电机转矩－转速的分布范围，可以看出，变桨电机的运行点集中在第I、III、IV象限，并且在电机正向转速即正向变桨过程中，转速基本在1700rpm以内，转矩在-80Nm～40Nm范围内，而反向转速包络在500rpm以内，转矩值集中在-100Nm～-20Nm范围内，此时变桨电机承受峰值转矩工况。相比于DLC1.2疲劳工况包络范围，DLC2.3极限工况对变桨电机转速要求更高。

（三）两种工况变桨载荷计算结果

对变桨系统的两种典型载荷仿真计算结果进行对比，如表1及表2所示。

对变桨电机的基本需求是高性能长期运行于疲劳载荷工况，能够承受极限载荷工况。一般而言，变桨电机的峰值转矩出现在极限工况，考虑数据裕度以及运行时间等原因，此计算结果的峰值转矩出现在疲劳工况，而峰值转矩对应的转速远小于极限工况，即对变桨电机的功率需求要依据极限运行状态的最大功率。

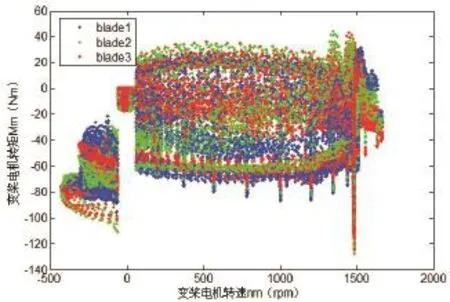
图9 DLC2.3工况变桨电机转矩-转速载荷分布

三、基于变桨载荷分布的状态参数相关性分析

基于变桨载荷的分布特征以及变桨状态参数的相关性分析可以评估变桨系统能力与状态以及确定稳定运行域。图10为转矩值与桨距角的相关性分析及统计，表明变桨电机的均方根转矩与桨距角之间存在相关关系，从而确定变桨系统的稳定运行域，对系统健康度进行估计与监控。

变桨系统数据驱动控制建模

对变桨系统进行精确化建模是控制系统实现高性能的前提。在多数情况下被控对象的精确模型是不可知的，而目前广泛应用的控制方法都是基于模型的控制。对于变桨系统，精细化的机理建模涉及气动与机电控制耦合以及模型尺度问题，模型维数及非线性特征明显。目前典型的变桨系统建模方法采用阶跃响应时域辨识或者频域辨识等方法，通过测试或运行数据对变桨系统的线性化传递函数模型进行系统阶次和参数辨识。

基于上述对变桨载荷的仿真计算以及载荷分布特征，按照变桨系统载荷转矩－转速分布规律进行变桨系统加载。图11为变桨系统数据驱动建模的结构框图，采用正交最小二乘方法对包含时滞特性的阶跃响应数据进行模型辨识。需要明确的是，此种数据驱动建模方法得到的变桨系统的线性模型是静态的，模型的获取可以采用两种方法：开环辨识与闭环辨识。对于变桨控制回路，开环辨识时可将纯滞后环节与二阶传函结构相分离，把对象的高阶特性简化为低阶形式，保留其最基本的一阶或二阶主导特性外把其他因素都合并在纯滞后中，采用分步辨识即可得到某运行状态时的变桨系统模型。

表1 DLC1.2工况各风速下20年模拟运行变桨系统平均转矩与转速计算结果

表2 DLC1.2与DLC2.3工况变桨系统转矩与转速峰值及额定值计算结果

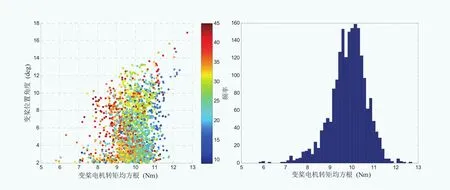
图10 变桨电机转矩与桨距角的关联分布

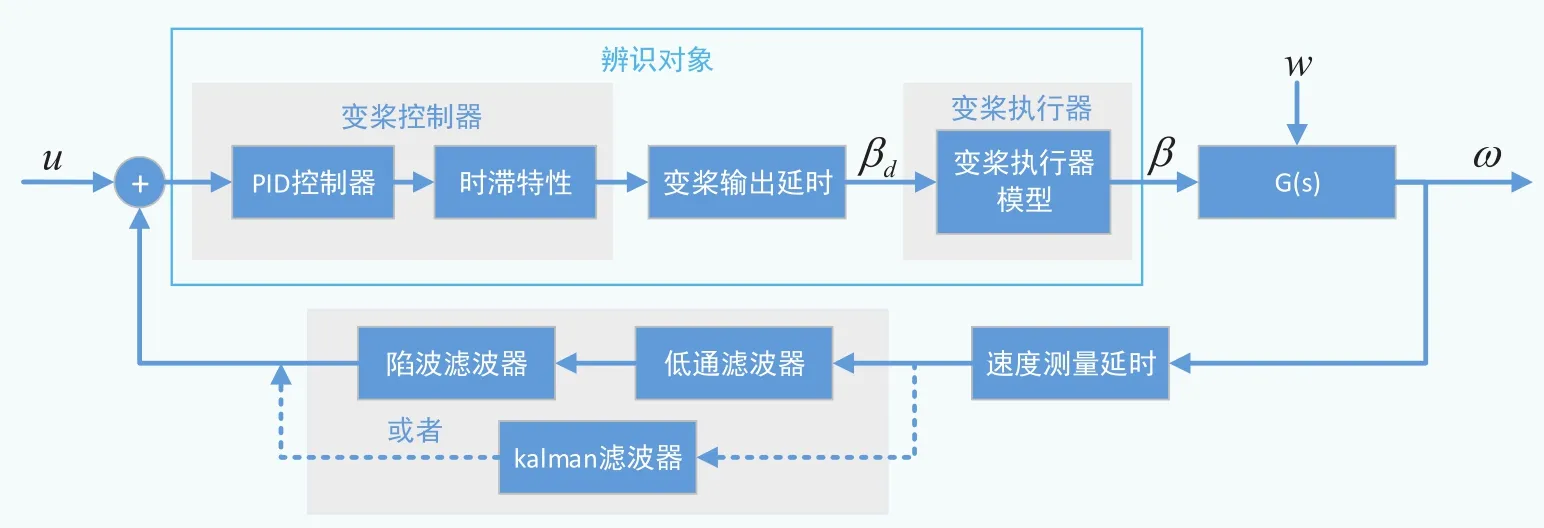
图11 变桨系统数据驱动控制辨识结构框图

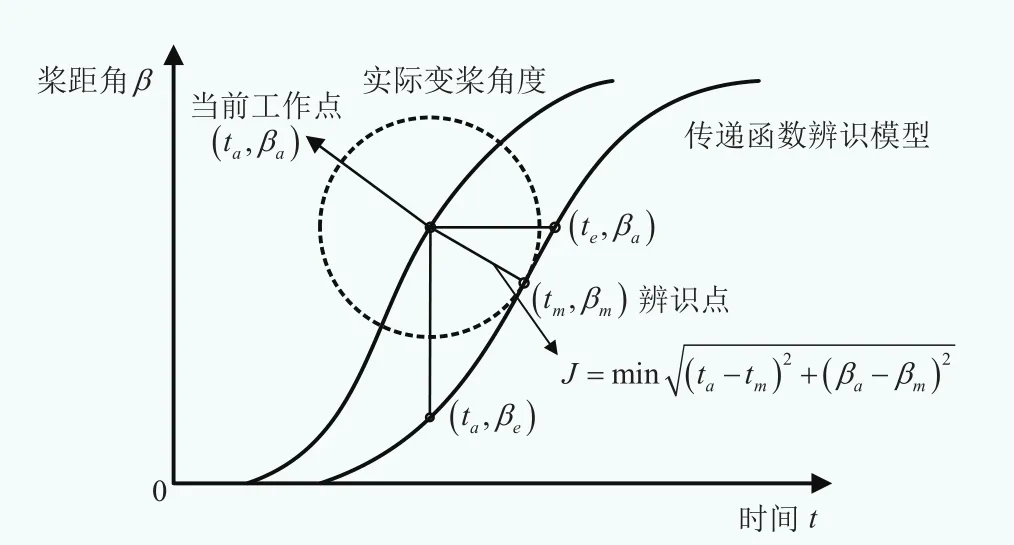
图12 数据驱动建模参数辨识的正交化方法

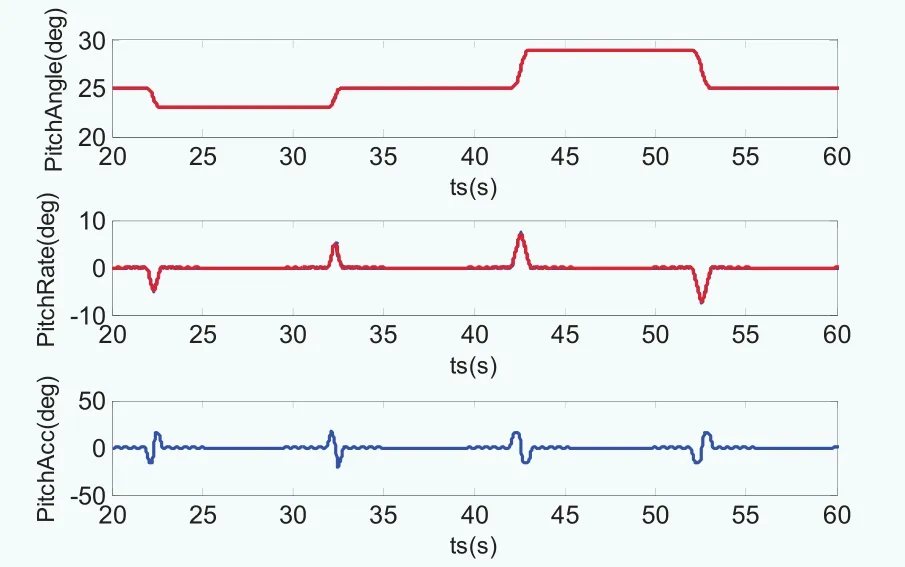
图13 滤波后的变桨角度、速度及加速度信号

理论上，模型辨识结果应该和实测结果拟合得越精确越好，但对于实际变桨系统来说是不合理的，这源于两个方面原因：其一，变桨系统是机电耦合的复杂伺服控制对象，既要保证动态响应的快速性以及硬件的物理限制，又要保证稳定精度；其二，对于阶跃响应，总是希望起始和接近稳定时的速度较平缓，而中间过程能够快速过渡。因此基于变桨系统数据驱动的模型辨识过程中需要增加3个约束以保证：（1）实测桨距角曲线不超出规定范围；（2）变桨速度和加速度满足限制约束；（3）动稳态性能满足要求。选取评价指标为辨识模型桨距角曲线与实测桨距角曲线的正交距离最小，如图12所示。

基于变桨系统的输入－输出阶跃响应数据进行传递函数模型辨识，输入量为期望桨距角阶跃信号，输出量为实测桨距角，按照前述的变桨载荷分布特性进行模拟加载。对实测信号进行延时处理与数据滤波等，结果如图13至图16所示。

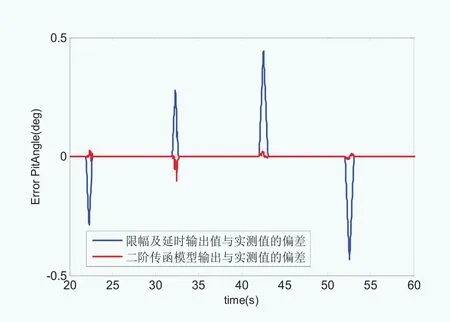
图14 变桨角度动态偏差

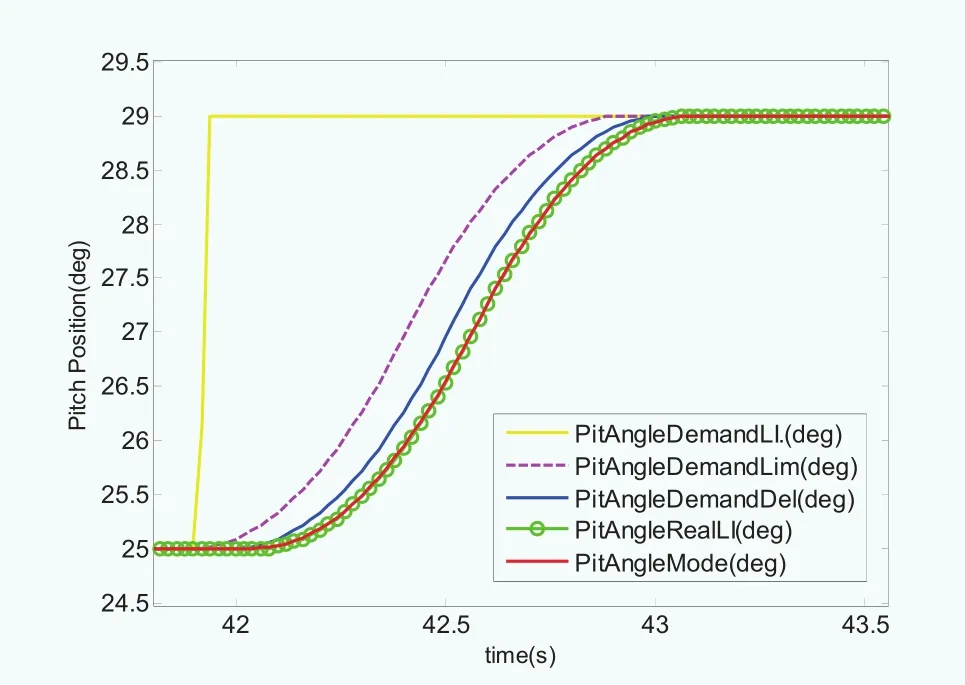
图15 变桨正向阶跃响应模型辨识结果

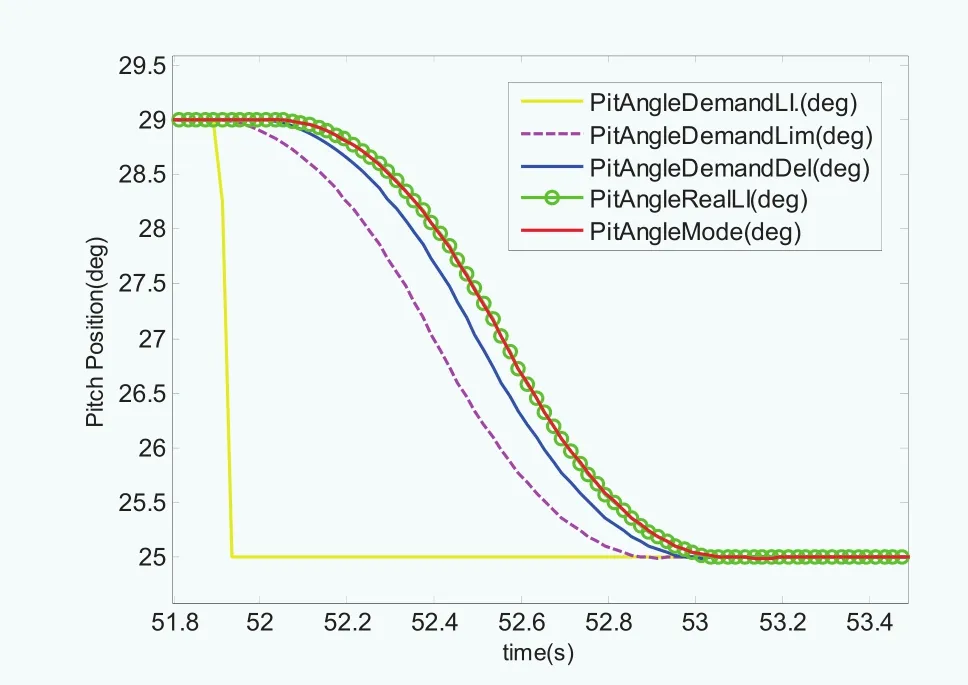
图16 变桨负向阶跃响应模型辨识结果

变桨系统的控制输入为桨距角阶跃信号，幅值分别为±2度、±4度等。图13为滤波后的桨距角、变桨速度及加速度信号与期望信号的对比，考虑输出信号的延时，可见桨距角信号能够较好地跟踪期望信号，并且变桨速度及加速度信号满足限制值要求。图14为辨识模型输出信号和限幅延时输出信号与测量值的桨距角动态偏差，其中辨识模型动态偏差基本保持在0.02度范围内，最大偏差为0.1度，满足动态要求。图15与图16分别为正向阶跃响应与负向阶跃响应模型辨识输出信号对比，其中PitAngleDemandLI为期望桨距角信号，PitAngleDemandDel为考虑变桨速度限制和变桨加速度限制以及时滞参数的物理限制边界，即辨识模型输出信号不能超出此物理限制边界，以避免硬件过度损耗。PitAngleRealLI为实际测量桨距角信号，PitAngleModel为辨识模型输出信号，在满足前述的3个附加约束基础上，辨识模型输出信号PitAngleModel能够较好地跟踪实际桨距角信号，并且保证实测桨距角曲线PitAngleRealLI处于PitAngleDemandDel和PitAngleModel范围之内。对比图15与图16的阶跃响应，在相同变桨载荷及约束条件下的正反向阶跃响应拟合模型基本一致，由模型辨识结果可以得到变桨系统的二阶时滞传递函数模型：

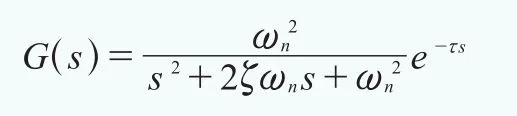
其中：阻尼系数ζ为0.86～0.92，自然振荡频率ωn的范围为6Hz～6.5Hz，延时τ为0.12s。基于变桨系统的二阶传递函数模型，通过附加反馈－前馈回路提高变桨系统阻尼比，减小超调量，加快响应速度，并且可以很好地对高频噪声滤波，增强系统的抗干扰能力，改善系统动稳态性能。

结论

变桨载荷计算分析与控制建模是实现高性能变桨控制的前提。本文从变桨载荷计算与控制的角度，提出电动变桨系统载荷智能化计算与分析方法，可以充分挖掘变桨载荷信息，用于变桨系统关键参数计算、运行包络范围确定、载荷校核与控制器反馈设计以及相关分析故障诊断等，大大提高计算效率与自主设计能力。对结合载荷分布特征的变桨系统数据驱动建模，提出基于正交最小二乘数据驱动建模方法进行变桨系统阶跃响应模型参数辨识，得到变桨系统数据驱动时滞二阶传函模型，对于分析变桨系统动稳态性能具有重要意义。