风电机组叶片覆冰状态与动力学特性的定量关系研究*

文 | 陈志刚，李录平，杨波，刘胜先，封江，龚妙

我国的疆域辽阔，气象条件复杂，在北部地区的陆地和海上，南部地区的高海拔山区等，冬季的风雪霜冻给风电机组的运行带来了极大危害。运行在冬季湿冷地区的风电机组，在冬季经常会出现严重覆冰现象。工作中的风电机组叶片覆冰后，会破坏风电机组叶片的动力特性与气动特性，冰的质量、刚度等性质会影响叶片的材料特性，造成叶片过载及载荷不均匀，使其特性与设计初衷不符，造成风电机组不能正常发电，甚至导致严重的安全事故。及时、准确地检测出叶片的覆冰状态，便于对风电机组采取及时有效的运行和维护措施，对提高风电场运行的安全可靠性和经济性，具有重要意义。

自20世纪90年代开始，对于构件覆冰检测的研究已经引起人们广泛关注，研究对象主要集中在航空领域（如飞机），主要的测量方式包括：机械法、电学法、热学法、光学法、波导法等。但是，目前直接用于风电机组叶片覆冰检测的研究仍然比较少，能够成熟用于工程实际的风电机组叶片覆冰检测方法与技术仍少有资料报道。

本文探索一种利用叶片模态参数变化特征来检测叶片覆冰状态的方法：以翼展1120mm（不包含叶片根部）长的小风电机组叶片为研究对象，在Solidworks平台上建立起三维实体模型。建立在振动力学、动力学分析以及柔性多体动力学理论基础上，在ANSYS结构分析软件中对该叶片在覆冰前后状态下模态进行分析，得到前6阶固有频率和振型，比较覆冰前后风电机组叶片动力特性的变化情况，提取叶片覆冰后的振型曲率变化特征，获得诊断叶片覆冰程度、覆冰位置的基本方法，为工程实际中诊断叶片覆冰故障提供理论依据。

研究对象简介

本文以一小型风电机组叶片为研究对象，在三维制图工具软件Solidworks中建立风电机组叶片三维实体模型（见图1）。如图1所示，叶片为弦长140mm的等截面直叶片，内部为实体结构，长度为1120mm，由一种翼型界面拉伸而成。

图1 模拟风电机组叶片三维实体模型

图2 叶片结冰沿翼展方向分布示意

叶片覆冰状态描述模型

风电机组叶片覆冰的空间分布描述采用如图2所示的模型，假设叶片在某一区段附着一定厚度的冰，其覆冰状态（Blade Icing Condition，简称BIC）信息用下式描述：

式中，x是叶片覆冰段沿翼展方向的起始坐标（相对坐标值）；Δx是叶片覆冰段沿翼展方向的长度（相对值）；λ是叶片覆冰段的覆冰厚度（相对坐标值）。

一、覆冰区域起始点坐标参数

定义叶片覆冰的起点坐标参数为x（见图2），其表示的是沿翼展方向覆冰区域的起始点相对位置，参数为一个无量纲量。以叶片与轮毂的结合处为翼展方向坐标原点，定义描述覆冰起始位置的坐标参数计算公式为：

式中，L是所测风电机组叶片的翼展长度，m；X是覆冰段起始点距离叶根的坐标，m；x的取值范围为：0～1。

二、覆冰区域长度参数

定义覆冰长度参数为Δx，其表示在翼展方向覆冰区域沿翼展方向的相对长度。设覆冰段起点端到另一端的长度为 ΔX（见图2），定义描述覆冰区域相对长度参数的计算公式为：

式中，ΔX是覆冰段沿翼展方向的长度，m。Δx的取值范围为：0～1。

三、覆冰厚度参数

根据风电场的风能资源条件，风电机组叶片的结构大小多种多样，因此用冰层厚度的绝对值不能准确反映风电机组叶片覆冰厚度。因此，定义覆冰厚度相对值λ，用其描述覆冰区域平均覆冰厚度：

式中，d是所测风电机组叶片覆冰区域平均覆冰厚度，m。

覆冰叶片动力学特性计算数学模型

一、覆冰叶片等效材料特性参数计算模型

采用有限元方法计算覆冰叶片的动力学特性前，需要对比覆冰前与覆冰后叶片材料性能参数的变化情况。为此，本文在计算叶片中取中间一段180mm长的叶片段，建立叶片片段覆冰模型，覆冰相对厚度λ取值范围为0～8.035714（1～9mm厚度）。根据所设置的叶片材料密度和冰层密度，用Solidworks软件计算出叶片结构的质量变化情况。图3、图4所示为叶片段相对覆冰厚度λ分别取值为0.0、2.0时的覆冰模型。

图3 叶片片段λ为0的模型

图4 叶片片段λ为2的覆冰模型

图5 叶片片段结构网格化图

图6 叶片片段λ为2的结构网格化图

将覆冰前后的叶片段结构导入ANSYS中，分别进行力学分析，在覆冰叶片段组合体中定义叶片材料的弹性模量E＝4.26e10，泊松比为0.22，密度为1950kg/m3；冰的弹性模量E＝2e9，泊松比为0.1，密度为900kg/m3。由于计算对象为小叶片，所以定义叶片为Solid45实体模型，网格化以后得到图 5－图6。

定义叶片段的一端为全约束，在叶片的另一端Y轴反方向施加一个50N力载荷，载荷施加图和软件计算后的结构变形图如图7、图8所示。

在叶片段的一端设置全约束，另一端施加一个力偶载荷产生5N・m力矩，通过ANSYS软件计算得到覆冰叶片结构的扭转变形图，如图9所示。通过施加力和扭矩（力偶）分别得到叶片的弯曲变形和扭转变形，在施加外界载荷中力和扭矩不变的条件下，分别对不同覆冰相对厚度的叶片进行结构受力变形计算。

本文采用的抗弯刚度实验测量公式为：

采用的扭转刚度实验测量公式为：

式中，F为结构所受力载荷，N；M为结构所受力偶载荷， N・m；y为结构在力载荷下的位移，m；θ为结构在力偶载荷下的扭转角度，deg。

首先根据式（5）、（6）计算得到覆冰叶片片段结构的抗弯刚度和扭转刚度，结合质量变化、抗弯刚度及扭转刚度计算得到三项参数变化率随覆冰厚度增加的变化关系图，如图10所示。

从图10中可以看出，叶片的相对覆冰厚度λ从0到8之间变化时，叶片材料等效性能参数呈现如下变化规律：

（1）叶片覆冰后，材料等效质量、等效弯曲刚度、等效扭转刚度均有不同程度增加；

（2）叶片的等效质量随覆冰的相对厚度几乎呈线性增加，当相对覆冰厚度λ达到8时，叶片的等效质量增加近35%左右；

（3）当覆冰相对厚度λ在 4.5以内时，叶片的等效弯曲刚度随覆冰厚度的增加呈现快速增加趋势，之后，随着覆冰相对厚度的继续增加，等效弯曲刚度增加的趋势减缓，当覆冰厚度达到8时，叶片的等效弯曲刚度增加近35%左右；

（4）当覆冰相对厚度λ在4.5以内时，叶片的等效扭转刚度随覆冰厚度的增加呈现缓慢增加趋势，之后，随着覆冰相对厚度的继续增加，等效扭转刚度增加的趋势加快，当覆冰厚度λ达到8.0时，叶片的等效扭转刚度增加近12%左右。

图7 叶片片段λ为0的弯曲变形图

图8 叶片片段λ为2的弯曲变形图

图9 叶片片段λ为2的扭转变形图

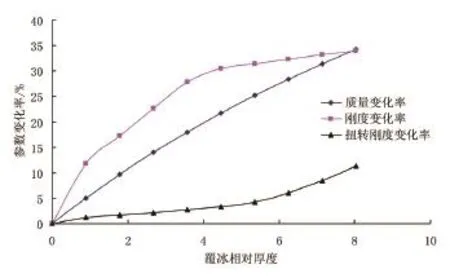
图10 叶片片段在不同覆冰相对厚度下的材料性能变化图

二、覆冰叶片模态参数变化量计算模型

（一）叶片模态频率变化量计算模型

将叶片在挥舞方向的振动问题简化成在根部固接的悬臂弯曲振动问题。悬臂梁的模态频率计算问题可演化成由下式描述的特征值问题：

式中，K和M分别是叶片整体刚度矩阵和质量矩阵；φ是正则化振型；ω是模态频率。假定风电机组叶片覆冰使叶片结构刚度矩阵和质量矩阵都产生一个细微摄动量，则对φ和ω也会产生一个细微改变量，改变后的振动方程为：

式中，ΔM，ΔK和Δφ分别为叶片结构的质量矩阵、刚度矩阵和振型的改变量。

对风电机组叶片这样的变截面悬臂梁结构，在不同的覆冰厚度情况下，覆冰对质量矩阵的影响程度和刚度矩阵影响程度是不同的。对式（8）适当变形，得到：

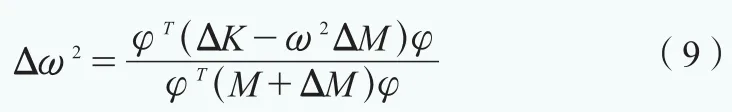
在某一阶振型下，有：

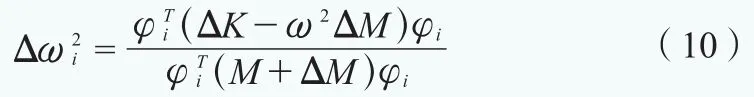
式（9）、（10）中，φT表示正则化振型矩阵φ的转置矩阵。从上两式可以分析得出，若刚度增加则叶片结构自振频率增加，刚度降低则结构频率会降低；而质量增加，结构频率就会降低，反之，结构频率会增加。

（二）叶片模态振型曲率计算模型

由于风电机组叶片为悬臂梁结构，因为挥舞方向的抗弯能力最差，所以变形主要以挥舞方向弯曲变形为主，因此采用梁结构单元进行推导，其振动微分方程为：

式中，x表示梁的轴向方向的坐标；I（x）表示梁的抗弯截面模量；E、ρ分别表示材料的杨氏模量和密度；A（x）表示梁的截面积；C（x）表示材料的阻尼；y（x,t）表示梁的变形（位移）；f（x,t）表示作用在梁上的外力。

根据模态分析理论，式（11）的解可表示为各阶模态振型的叠加形式：

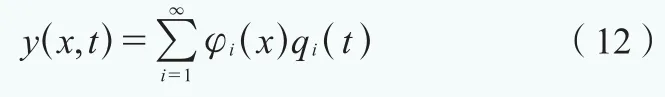
式中，φi（x）为位移模态振型；qi（t）为模态坐标；i为振型阶数。

根据梁结构单元振动微分方程式（11）和振动位移公

式（12），将式（11）化简得到：

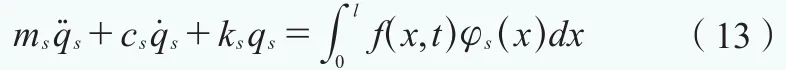
式中，ms、cs、ks分别表示梁的第s阶模态质量、阻尼和刚度；φs表示梁的第s阶模态振型；qs表示梁的第s阶模态坐标。

根据材料力学给出的梁结构静力弯曲关系：

式中：M是叶片弯矩，ρ是曲率半径。

设f（x,t）＝F（x）ejωt，由上两式得到 ：

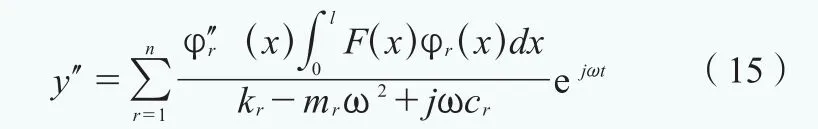
曲率是位移的二阶导数，将上式离散化后得到：

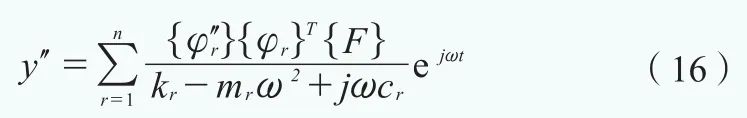
矩阵形式为：

其中：

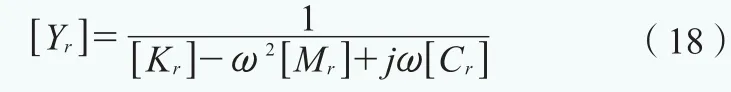
y′′的微分增量为 ：

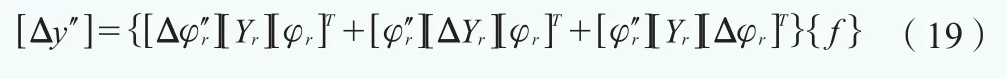
覆冰叶片模态特性变化规律计算与分析

一、覆冰叶片模态频率变化量计算与分析

在Solidworks中建立叶片覆冰模型。图11－图13分别表示在叶片不同覆冰起点位置上覆上一定长度区域的冰，并对不同覆冰状态下的叶片进行模态分析。

采用ANSYS软件，对不同覆冰情况下的叶片进行模态分析，得到频率以及振型数据。叶片与冰的材料参数定义同上，将所有频率数据整理出来，计算出相对于未覆冰状态下叶片结构的频率变化率（图14）。图14中曲线说明有三个参数，第一个参数表示覆冰起点x，第二个参数表示覆冰长度Δx，第三个参数表示相对覆冰厚度λ。

图14中包含所测叶片结构前六阶模态频率。其中，从第一阶频率至第六阶频率分别为挥舞一阶振型频率、摆振一阶振型频率、挥舞二阶振型频率、挥舞三阶振型频率、扭转一阶振型频率和挥舞四阶振型频率。

图11 覆冰起点x＝0.25，覆冰长度Δx＝0.5，覆冰厚度λ＝4时叶片三维图

图12 覆冰起点x＝0.25，覆冰长度Δx＝0.25，覆冰厚度λ＝4时叶片三维图

图13 覆冰起点x＝0.75，覆冰长度Δx＝0.25，覆冰厚度λ＝2时叶片三维图

从图14可以发现：

（1）叶片表面覆冰后，会导致模态频率的变化；覆冰越严重，模态频率的相对变化值越大。

（2）不同覆冰状态下各阶模态频率的变化率也是不同的。整体而言，叶片覆冰对一阶模态频率影响最大。

（3）当叶片所有表面覆冰时，叶片模态频率变化最大且与覆冰厚度成正比关系。

（4）叶片根部覆冰后导致叶片结构刚度增加明显，故模态频率升高；叶片叶尖区域覆冰后导致叶片结构质量增加明显，引起模态频率下降。

图14 不同覆冰状态下叶片结构前六阶模态频率变化

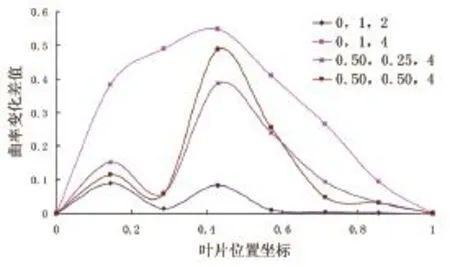
图15 叶片各点在不同覆冰条件下一阶曲率变化率

二、叶片覆冰状态与叶片模态振型的关系

由于叶片覆冰后，结构刚度显著增大，导致的曲率变化［Δy′′］，主要由［Δφ′′r］［ΔYr］［Δφr］三者共同作用。而［Δy′′］ 与［Δφ′′r］的变化在叶片位置坐标上存在统一对应性的变化。

用ANSYS软件仿真计算出的叶片结构固有特性参数包括模态频率和模态振型，所获得的模态振型主要以位移模态数据为主。根据差分法计算出叶片结构的各阶曲率模态参数。这里主要分析叶片结构的挥舞方向的模态曲率，根据下式得出叶片结构的曲率变化率曲线图，如图15所示。

式中：ξi为i点处覆冰后的曲率变化率；φwi为i点处覆冰后曲率值；φfi为i点处无冰状态下曲率值。

从图15中可以看到：

（1）在叶片全覆冰情况下，覆冰2mm时曲率变化较小，曲率变化率曲线无规则；当覆冰达到4mm时曲率变化明显增大，同时曲率变化率曲线呈现明显的抛物线形状。由此可见，在覆冰区域一定时，覆冰厚度越大，叶片模态振型曲率的变化率越大。

（2）覆冰起点为0.5，覆冰长度分别为0.25和0.50时，叶片对应位置的曲率变化率曲线也有凸起形状，同时可以看出覆冰长度Δx＝0.50的曲率变化率大于覆冰长度Δx＝0.25的曲率变化率。由此可见，在覆冰起点位置相同时，覆冰区域越大，叶片模态振型曲率的变化率越大。

从上述分析结论可以看出，通过对覆冰前后叶片结构的曲率变化进行分析研究，能够进一步对覆冰状态进行判断。

摄影：李博

结论

本文提出了风电机组叶片覆冰状态的空间描述模型，给出了叶片覆冰起点参数、覆冰长度参数和覆冰厚度参数的定义；给出了覆冰叶片动力学参数变化量计算模型。以一小型风电机组叶片为例，在Solidworks三维建模软件中建立三维实体模型，应用ANSYS结构分析软件对风电机组叶片进行有限元模型分析，通过有限元计算，获得叶片在不同覆冰状态下的模态频率变化率、模态振型曲率变化率，通过分析发现：

（1）叶片覆冰区域靠近叶尖部分时，叶片模态频率呈现下降趋势；叶片所有表面覆冰时，模态频率变化率与覆冰厚度成近似正比关系。叶片根部区域覆冰后，叶片结构以刚度增加为主，故模态频率升高。叶片叶尖区域覆冰后，叶片结构以质量分布变化为主，导致模态频率下降。

（2）叶片模态振型曲率变化率值与叶片覆冰位置之间关系密切，根据叶片模态振型曲率变化率的不同，能够在一定程度上对不同覆冰情况下叶片覆冰位置和覆冰厚度进行判断。

（3）叶片模态频率变化率、模态振型曲率变化率与叶片覆冰状态具有明显的定量关系。工程实际中，通过这种定量关系，可以诊断叶片的覆冰故障。