基于自适应抗差卡尔曼滤波的UWB室内定位*

刘 韬,徐爱功,隋 心

(辽宁工程技术大学测绘与地理科学学院,辽宁 阜新 123000)

近年来,随着无线通信和无线传感器网络的不断发展,无线定位技术越来越受到人们的关注,广泛应用于灾害急救、目标跟踪、车载导航、行人导航等领域[1]。以全球卫星导航系统为基础的室外定位技术已趋于成熟;在室内定位中,超宽带UWB(Ultra-Wide Band)技术利用功率谱密度极低、脉冲宽度极窄的脉冲信号传输数据,具有时间分辨率极高、障碍穿透能力强等特点,在视距LOS(Line-Of-Sight)环境下能获得厘米甚至毫米级的测距和定位精度[2-3],适用于室内环境下的高精度定位。

由于墙体和障碍物的存在,UWB信号通过折射和反射在移动站和基准站之间进行传播,从而形成非视距NLOS(Non-Line-Of-Sight)误差,极大降低其测距精度,使定位结果产生较大的误差[4-8]。文献[4-5]对大量LOS和NLOS环境下的UWB信号波形特征进行分析,利用支持向量机进行NLOS状态的鉴别和误差削弱,能有效消除NLOS误差并提高测距精度,但该方法建立在大量的数据统计上,工作量较大;文献[6]针对LOS/NLOS环境下的定位,利用粒子滤波和无迹卡尔曼滤波方法进行定位和测速,能有效抑制NLOS误差的影响,但其算法复杂,实现困难;文献[7]利用基于往返时间RTT(Round Trip Time)和基于到达角度AOA(Angle Of Arrival)的方法进行混合测距,并提出了基于网格的聚类定位算法,其不需要室内环境的先验信息,仿真效果明显,但AOA方法需要天线阵列,会增加硬件成本;文献[8]利用惯性导航INS(Inertial Navigation System)辅助UWB进行定位,通过先验阈值进行NLOS判断,利用INS的短期高精度结果鉴别NLOS误差并消除其影响,但该方法需要增加硬件成本,且算法也更复杂。

UWB测距不仅会受到NLOS测距误差的影响,还会受到由实验环境、仪器硬件和人为干扰等因素产生的测距异常值的影响,这两个测距误差均表现为量测信息异常,从而导致距离滤波和定位解算出现异常。针对量测信息异常的问题,有学者提出抗差估计理论抵制量测信息异常误差的影响[9]。文献[10]结合神经网络和卡尔曼滤波构建自适应因子,自适应调节状态向量和量测噪声的协方差矩阵,从而抑制异常信息对滤波结果的影响,但神经网络需要大量理想的样本进行训练;文献[11]针对GNSS/INS组合系统,利用新息向量构建抗差因子并作用于量测噪声的协方差矩阵,从而修正滤波增益矩阵,提高系统的精度和抗差性。

在UWB定位中,很难用一个准确的统计特征来描述系统噪声。针对上述问题,本文提出了一种抗差自适应滤波算法并应用于UWB测距和定位。该算法首先在UWB距离模型的基础上,利用新息向量和LOS环境下的阈值鉴别量测信息是否出现异常,进一步构建量测噪声的抗差协方差矩阵,在滤波过程中利用改进的Sage-Husa滤波的次优无偏极大后验估计特性对系统噪声的协方差矩阵进行实时估计和修正,削弱并消除NLOS测距误差和测距异常值的影响,得到更准确稳定的测距信息;然后推导并构建UWB定位的线性模型,利用卡尔曼滤波得到载体的位置和速度信息。

1 距离滤波方法

1.1 距离模型

Xd,k=Fd,k-1Xd,k-1+wd,k

(1)

以RTT方法量测的距离值作为量测信息,则距离模型的量测方程为:

Zd,k=Hd,kXd,k+Vd,k

(2)

1.2 自适应抗差卡尔曼滤波

由于式(1)和式(2)组成的距离模型为线性模型,其标准卡尔曼滤波[8,14]KF(Kalman Filter)算法为:

(3)

(4)

式中:c为阈值,可通过UWB基准站和流动站之间为LOS环境下多次测量确定。采用Huber函数[9-11]方法构建量测噪声的抗差协方差矩阵,即:

(5)

在UWB测距过程中,很难用一个准确的统计特征来描述系统噪声,而Sage-Husa滤波能对系统噪声统计特性进行实时估计和修正,从而进一步提高滤波的精度,且具有一定的抗干扰能力[15-17]。结合文献[16],利用改进的Sage-Husa滤波对系统噪声的协方差矩阵进行实时估计:

(6)

在计算预测状态协方差矩阵时,利用式(6)对系统噪声的协方差矩阵不断进行实时估计和修正,进而减小状态估计误差,并结合式(5),实现UWB距离模型的自适应抗差卡尔曼滤波ARKF(Adaptive Robust Kalman Filter)过程,在抑制量测信息异常误差的同时进一步提高滤波解算的精度,得到更准确可靠的UWB测距信息。

针对自适应抗差卡尔曼的距离滤波方法,利用一组静止的UWB测距信息进行分析验证。静止数据由Time Domain的PulsON400通信与测距模块采集,采样频率为2 Hz,共采集2 000 s,数据采集过程中有人员在UWB基准站和流动站之间随机走动,同时对UWB天线进行随机遮挡。原始的RTT测距信息如图1所示。

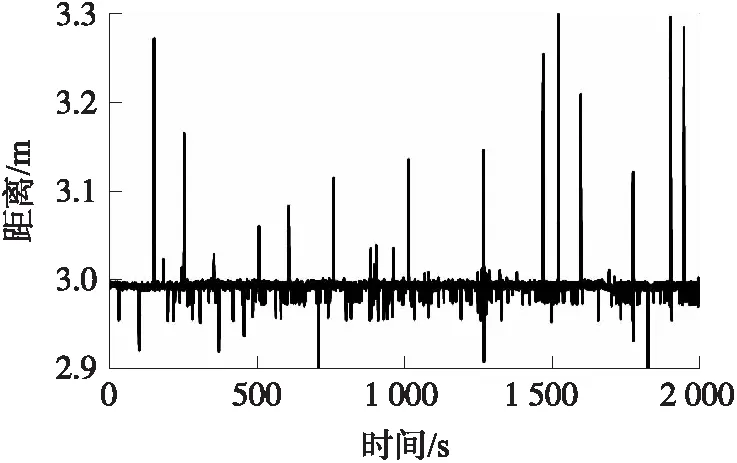
图1 RTT测距信息

由图1可以看出测距中存在大量的NLOS误差和测距异常值。在对标准时间偏差误差进行改正之后,利用卡尔曼滤波、Sage-Husa自适应滤波和文中的自适应抗差卡尔曼滤波方法进行滤波计算,利用全站仪观测计算的距离作为参考真值进行比较分析。

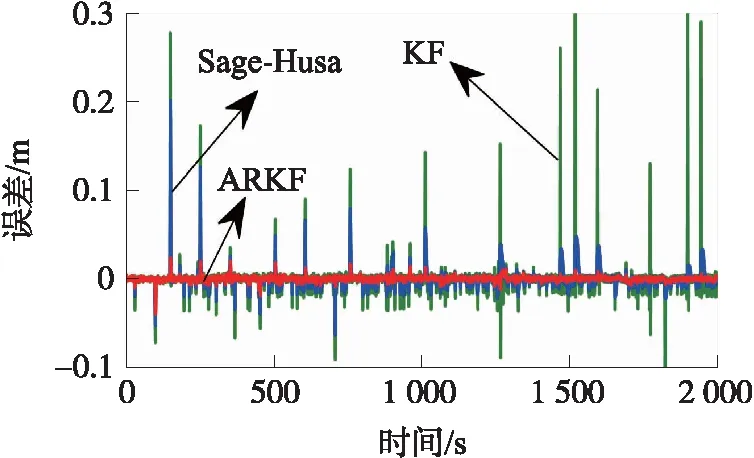
图2 3种滤波方法的测距误差

图2给出了3种方法的测距误差,表1给出3种方法的误差统计信息。结合图2和表1,相较于卡尔曼滤波和Sage-Husa自适应滤波,自适应抗差卡尔曼滤波的最大误差能从3 dm降低至4 cm,其测距精度更高、稳定性更强。可以看出:自适应抗差卡尔曼滤波方法利用抗差估计理论能有效抑制UWB测距中的NLOS测距误差和测距异常值,同时结合Sage-Husa自适应滤波对系统噪声进行实时的估计和修正,进而提高UWB测距的精度和稳定性。

表1 3种滤波方法的测距误差统计

2 UWB定位方法

在UWB平面定位中,利用3个及3个以上置于固定位置的UWB基准站和1个流动站进行定位[8,18]。以流动站的位置和速度信息作为状态参数Xp,k=[xkykvx,kvy,k]T,则UWB定位的状态方程为:

Xp,k=Fp,k-1Xp,k-1+wp,k

(7)

式中:xk和yk分别为第k时刻UWB流动站在x和y方向的位置,vx,k和vy,k分别为第k时刻UWB流动站在x和y方向的速度,Fp,k为系统状态转移矩阵,wp,k为系统噪声,wp,k为零均值的高斯白噪声,其对应的协方差矩阵为Qp,k,且有:

(8)

(9)

式中:ΔTk为UWB数据采样间隔,q为系统噪声的功率谱密度。

通过距离滤波方法对原始RTT测距信息进行处理,削弱并消除测距中的NLOS测距误差和测距异常值的影响,得到更准确可靠的测距信息。那么,第k时刻第i个UWB基准站和流动站之间的距离di,k可表示为:

(10)

对式(10)进行变形后,可以得到:

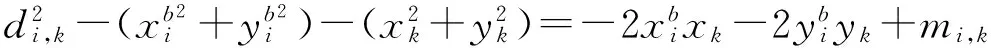
(11)

Zp,k=Hp,kXp,k+Vp,k

(12)

式中:Hp,k为量测矩阵,Vp,k为k时刻的量测噪声,Vp,k为零均值的高斯白噪声,其对应的协方差矩阵为Rp,k,且有:

(13)

(14)

在UWB定位的状态方程和量测方程中,其系统噪声和量测噪声互不相关。由于式(7)和式(11)组成的UWB定位模型为线性模型,在假设系统噪声和量测噪声为高斯白噪声的前提下,利用式(3)的卡尔曼滤波方法能最优估计UWB流动站的位置和速度信息。

图3 室内实验场景

3 实验与分析

实验数据由Time Domain的PulsON400通信与测距模块采集,其带宽为3.1 GHz～5.3 GHz,数据采样频率为2 Hz,利用RTT方式测得UWB流动站与基准站间的距离,在LOS环境下测距精度为厘米级。为了验证本文算法的有效性,分别利用卡尔曼滤波(KF)、Sage-Husa自适应滤波(Sage-Husa)和文中的自适应抗差卡尔曼滤波(ARKF)进行距离滤波,然后再进行定位解算。在如图3所示的室内环境下分别进行静态定位和动态定位实验。

静态实验中,将3个UWB基准站置于固定位置,利用全站仪确定其坐标,并假设其没有误差,UWB流动站静止不动,以全站仪观测的UWB流动站坐标作为参考真值,实验时长约为6 min,实验过程中有多人随机在实验场中走动。图4给出3个UWB原始的RTT测距信息,可以看出其中存在部分的NLOS测距误差和测距异常值,图5和图6给出了3种滤波方法在x和y方向上的定位误差,表2给出了3种滤波方法的误差统计。

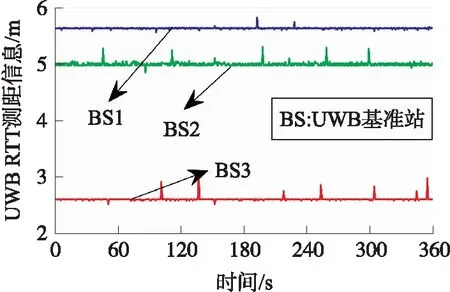
图4 静态实验中的UWB测距信息

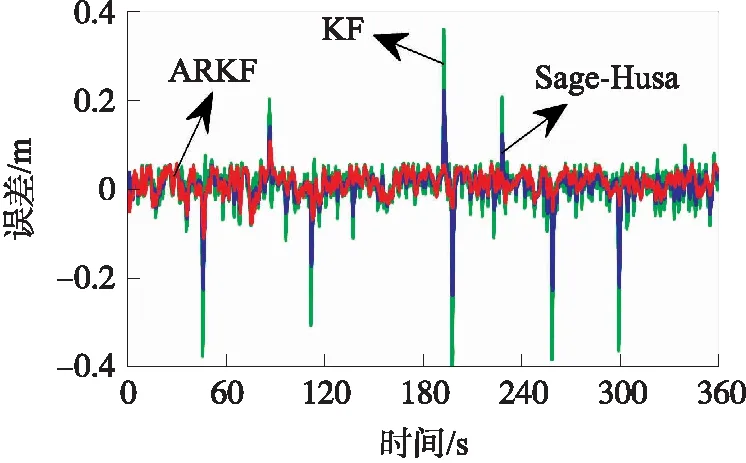
图5 3种滤波方法在x方向的位置误差

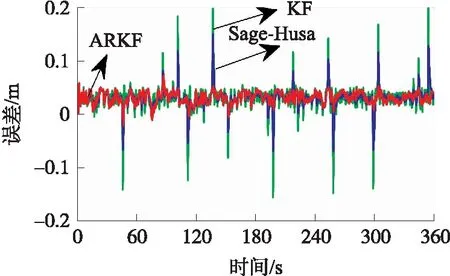
图6 3种滤波方法在y方向的位置误差

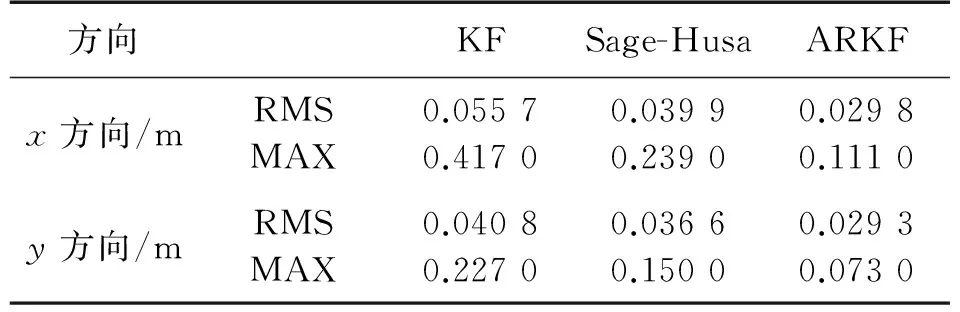
表2 静态实验中3种滤波方法的误差统计

在动态实验中,将3个UWB基准站置于固定位置,利用全站仪确定其坐标,并假设其没有误差,将UWB流动站置于实验小车上,人员推着实验小车移动,利用全站仪确定的UWB流动站的位置作为参考轨迹,实验时长500 s。图7给出了3个UWB原始的RTT测距信息,其中蓝色、红色和绿色线分别为测得的第1个、第2个和第3个UWB基准站与流动站之间的距离,由于遮挡导致测距中存在NLOS测距误差和测距异常值。

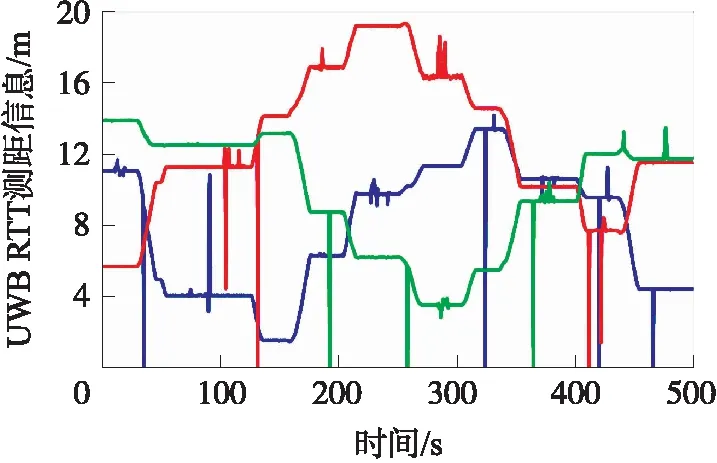
图7 动态实验中UWB测距信息

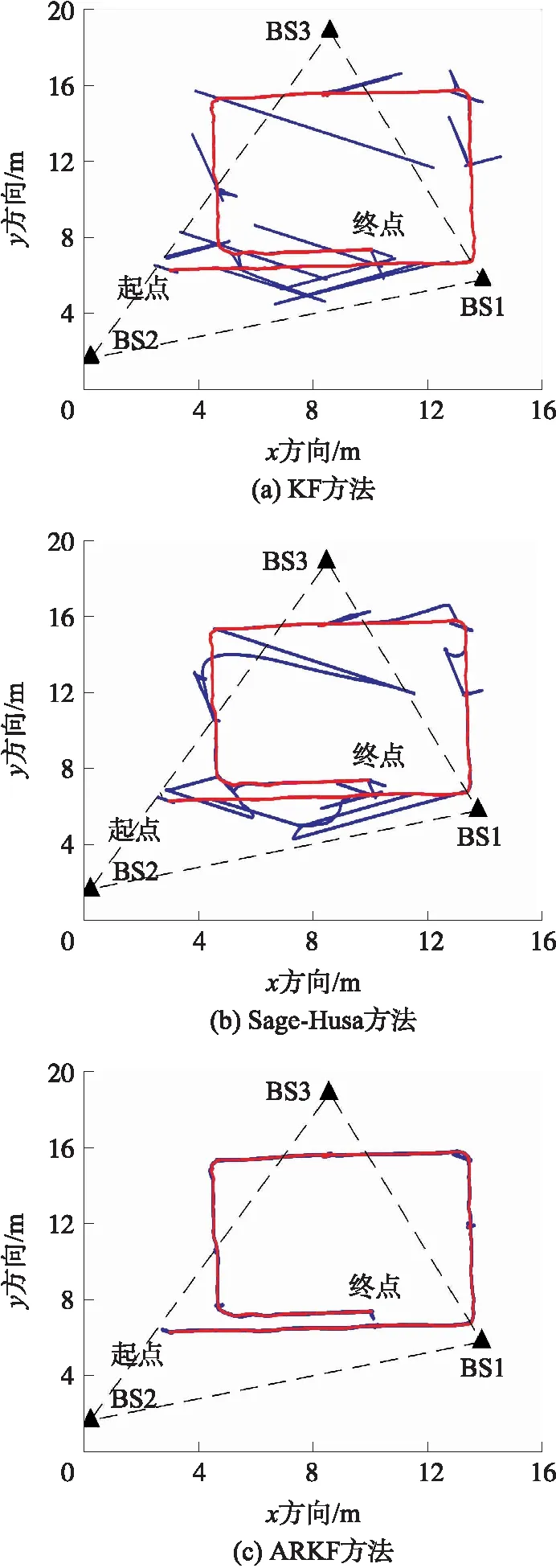
图8 动态实验中3种滤波方法解算的动态轨迹

利用3种方法进行距滤波,然后进行距离解算,图8给出了3种方法的平面轨迹,其中红色实线为参考轨迹。图9和图10分别给出了3种滤波方法在x和y方向上的定位误差,其中绿色、蓝色和红色线分别为KF、Sage-Husa和ARKF方法的误差,表3给出了3种滤波方法的误差统计。

图9 动态实验中3种滤波方法在x方向的位置误差

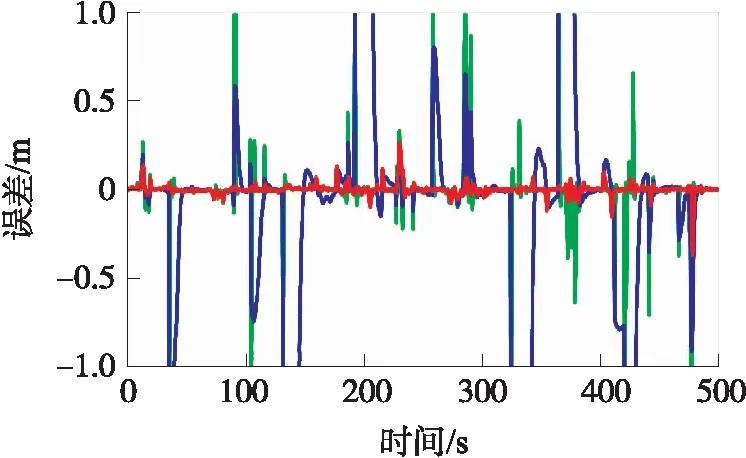
图10 动态实验中3种滤波方法在y方向的位置误差

方向KFSage-HusaARKFx方向/mRMSMAX0.4357.4901.5126.6940.0480.531y方向/mRMSMAX0.2513.6450.9113.4030.0430.367

分析以上实验结果,可以得出:

①当UWB的RTT测距中出现NLOS测距误差和测距异常值时,利用卡尔曼滤波方法进行距离滤波时,其完全不具有抗差性,滤波结果误差较大,再进行定位解算时,UWB定位的精度和稳定性难以得到保障;

②利用Sage-Husa自适应滤波进行距离滤波时,静态情况下具有一定的抗差性,能提高测距的精度和稳定性,从而提高静态定位的精度和可靠性;然而在动态环境下,由于实验小车运动的不规律性,同时受到实验环境等因素的影响,很难同时精确地估计系统噪声和量测噪声,UWB定位结果的精度和稳定性难以提高,一旦滤波发散,错误的滤波值会污染测距良好情况下的定位结果,反而导致定位精度降低;

③利用文中提出的自适应抗差卡尔曼滤波进行距离滤波时,其依据抗差估计理论对NLOS测距误差和测距异常值进行抗差处理,能提高UWB测距的精度和稳定性,同时利用Sage-Husa自适应滤波对系统噪声进行估计和修正,能综合二者的优势,进一步提高距离滤波的精度和可靠性,进而得到精度更高、稳定性更好的UWB定位结果。

4 结论

在UWB室内定位中,测距过程中受到NLOS测距误差和测距异常值的影响,UWB定位精度会大幅下降,从而降低其稳定性和可靠性。本文将抗差估计理论和Sage-Husa自适应滤波用于UWB测距中的距离估计,并提出了针对UWB距离滤波的自适应抗差滤波方法,在此基础上推导了线性化的UWB定位模型,通过卡尔曼滤波计算载体的位置和速度信息。在室内环境下设计了UWB测距、静态定位和动态定位实验,将文中提出的方法与卡尔曼滤波和Sage-Husa自适应滤波进行了对比和精度分析。实验结果表明,文中提出的自适应抗差卡尔曼滤波方法能有效地消除并改正UWB测距中的NLOS误差和异常测距值,提高UWB测距的精度和稳定性,在此基础上利用卡尔曼滤波进行定位,能提升UWB定位的精度和可靠性。

参考文献:

[1] Liu H,Darabi H,Banerjee P,et al. Survey of Wireless Indoor Positioning Techniques and Systems[J]. IEEE Transactions on Systems,Man,and Cybernetics,Part C:Applications and Reviews,2007,37(6):1067-1080.

[2] de Angelis G,Moschitta A,Carbone P. Positioning Techniques in Indoor Environments Based on Stochastic Modeling of UWB Round-Trip-Time Measurements[J]. IEEE Transactions on Intelligent Transportation Systems,2016,17(8):2272-2281.

[3] Alarifi A,Al-Salman A M,Alsaleh M,et al. Ultra Wideband Indoor Positioning Technologies Analysis and Recent Advances[J]. Sensors,2016,16(5):1-36.

[4] Stefano M,Wesley M,Henk W,et al. NLOS Identification and Mitigation for Localization Based on UWB Experimental Data[J]. IEEE Journal on Selected Areas in Communications,2010,28(7):1026-1035.

[5] Wymeersch H,Maranò S,Gifford W M,et al. A Machine Learning Approach to Ranging Error Mitigation for UWB Localization[J]. IEEE Transactions on Communications,2012,60(6):1719-1728.

[6] Huerta J M,Vidal J,Giremus A,et al. Joint Particle Filter and UKF Position Tracking in Severe Non-Line of Sight Situations[J]. IEEE Journal of Selected Topics in Signal Processing,2009,3(5):874-888.

[7] 毛科技,邬锦彬,金洪波,等. 面向非视距环境的室内定位算法[J]. 电子学报,2016,44(5):1174-1179.

[8] 刘韬,徐爱功,隋心. 超宽带与惯性导航组合的室内导航定位[J]. 测绘科学,2016,41(12):162-166.

[9] Yany Y X,He H,Xu G. Adaptively Robust Filtering for Kinematic Geodetic Positioning[J]. Journal of Geodesy,2001,75(2):109-116.

[10] 高为广,陈谷仓. 结合自适应滤波和神经网络的GNSS/INS抗差组合导航算法[J]. 武汉大学学报(信息科学版),2014,39(11):1323-1328.

[11] 苗岳旺,周巍,田亮,等. 基于新息x2检测的扩展抗差卡尔曼滤波及其应用[J]. 武汉大学学报(信息科学版),2016,41(2):269-273.

[12] 徐爱功,刘韬,隋心,等. UWB/INS紧组合的室内定位定姿方法[J]. 导航定位学报,2017,5(2):14-19.

[13] de Angelis A,Nilsson J,Skog I,et al. Indoor Positioning by Ultrawide Band Radio Aided Inertial Navigation[J]. Metrology and Measurement Systems,2010,17(3):447-460.

[14] 王瑞荣,郑书万,陈浩龙,等. 一种基于Taylor和Kalman的室内协同定位方法[J]. 传感技术学报,2014,27(11):1557-1561.

[15] Sage A P,Husa G W. Adaptive Filtering with Unknown Prior Statistics[C]//Proceedings of Joint Automatic Control Conference,1969:760-769.

[16] 魏伟,秦永元,张晓东,等. 对Sage-Husa算法的改进[J]. 中国惯性技术学报,2012,20(6):678-686.

[17] Peng S,Chen C,Shi H,et al. State of Charge Estimation of Battery Energy Storage Systems Based on Adaptive Unscented Kalman Filter with a Noise Statistics Estimator[J]. IEEE Access,2017,5:13202-13212.

[18] Kok M,Hol J D,Schön T B. Indoor Positioning Using Ultrawideband and Inertial Measurements[J]. IEEE Transactions on Vehicular Technology,2015,64(4):1293-1303.