大型高精度GNSS基线向量网并行抗差估计
2015-11-07吕志平张友阳李林阳信息工程大学地理空间信息学院河南郑州45000郑州轻工业学院机电工程学院河南郑州45000
崔 阳,吕志平,张友阳,李林阳.信息工程大学地理空间信息学院,河南郑州45000;.郑州轻工业学院机电工程学院,河南郑州45000
大型高精度GNSS基线向量网并行抗差估计
崔 阳1,吕志平1,张友阳2,李林阳1
1.信息工程大学地理空间信息学院,河南郑州450001;2.郑州轻工业学院机电工程学院,河南郑州450002
针对大型GNSS基线向量网的特点,在改进的相关观测抗差估计RECO方案的基础上采用并行计算技术进行相关抗差估计的并行计算(简称“并行抗差估计”),并给出了可行的解算步骤。通过算例分析,验证了大型GNSS基线向量网的并行相关抗差估计,不仅有效抑制了观测异常对参数估值的影响,而且显著提高了计算效率。
相关抗差估计;GNSS;基线向量网;等价权矩阵;并行估计
1 引 言
随着越来越多的国家级或区域级CORS网络被部署,高精度GNSS基线向量网规模也越来越大[1]。受观测条件的影响,GNSS观测值中不可避免地带有粗差,而高精度GPS网粗差比例比常规大地测量网相对较大[2-3],使得大型高精度GNSS基线向量网粗差的处理更加繁琐。目前对于观测值带有相关性和异常影响的高精度基线向量网平差处理,通常采用相关观测抗差估计方法,如相关分析的方法[2]、基于标准化残差法[4]、IGGⅢ方案[3]及其改进[5]和RECO方案[6-7]及其改进[8]等,而这类相关抗差估计方法的实现均要进行选权迭代计算,使得涉及大型矩阵运算的相关抗差估计计算开销也大大增加。对于大型GNSS基线向量网的处理,由于粗差的复杂性和抗差能力的有限性,需要频繁试算以选择合适的抗差估计模型与参数;而且由于科学研究的需要和应用周期的缩短,经常面临采用不同的方案进行多次的平差计算,长时间的平差试算与分析降低了科学研究的效率。随着用户对大规模GNSS数据处理实时性的要求越来越高,研究提高抗差计算效率,将“事后计算”提高到“准实时计算”在定轨、机动测量保障、网络定位服务等应用领域具有重要意义。
对于运算复杂的大规模网平差问题,过去由于计算机内存和计算能力的限制,文献[2]推出了一种多维二次型矩阵压缩存储的快速直观算法以提高运算速度;文献[9]利用解算约化代替求逆约化,提出了一种分区平差快速解算新算法。随着个人计算机硬件平台的高速发展,提高硬件平台的性能利用效率和大规模数据处理的效率,对现有测量数据处理软件代码并行化或独立开发并行分布式软件系统成为解决测量数据处理的新方法[1015]。针对大型高精度GNSS向量网的抗差估计问题,本文在改进RECO方案基础上利用并行计算技术进行并行相关抗差估计的研究。针对基于消息传递接口(message passing interface,MPI)的并行算法设计复杂、消息传递和数据移动开销大问题,着重考虑当前主流的共享内存的多核系统优势,结合使用Microsoft在2010年发布的.NET4并行扩展开发工具并行任务库(Task Parallel Library,TPL),提出了一种基于任务划分的相关抗差估计多核并行算法,通过算例验证了大型GNSS基线向量网相关抗差估计并行算法的有效性,提高了硬件资源利用效率和抗差计算效率。
2 相关抗差估计模型的并行化
2.1 相关抗差估计模型
大型高精度GNSS网通常采用划分子网模型进行处理[2,16-17]。假设一个GNSS网划分为p个子网,得到m组基线向量组,各向量组的向量数分别为n1、n2、…、nm(n1+n2+…+nm=n),第i(i=1,2,…,m)个基线向量组的相关基线向量观测值Li建立的误差方程为

式中,常数项li=Li-AiX0,相关观测值Li的先验权矩阵为Pi。对m个基线向量组进行整网平差,则整网平差的误差方程为

式中由于向量组之间的观测值是独立的,所以全网的权矩阵P是由各个组向量权矩阵Pi组成的一准对角阵,则基于抗差M估计的选权迭代解式为


式中,¯P称为相关等价权阵。在双因子等价权模型中


式中γii和γjj称为自适应降权因子或收缩因子。在第k次迭代时,γii可取

式中

k0和k1称为阈值,根据实际情况选用不同的数值,一般取k0=1.0~1.5,k1=2.5~5.5。
式(7)单位权中误差计算公式中,n′等于观测量个数n减去淘汰观测量(γii为0)个数;median是中位数计算函数,通常是选择抗差性更高的中位数法计算单位权中误差[18-19]。为了在精度稳定的情况下获得最快求解效率,不同于采用IGGⅢ权函数,在文献[8]RECO改进方法的计算步骤基础上,将降权因子γ(k)ij求解公式中的平方改为可变参数t(t=1,2,…),并进一步改正了协方差阵Qv的求解公式。由于Qv的求解过程涉及等价权的求逆,而迭代过程中求逆非常耗时,通常采用不严密的方法进行简单处理,而在并行计算技术提供的高效率支撑下,可以采用更严密的方法进行抗差计算。剔除含粗差的情况会导致等价权求逆失败,本文采用降维求逆或者对剔除粗差的等价权对角元素赋固定值(如10-6)的方法。图1是完善后经实践证明可行的步骤。
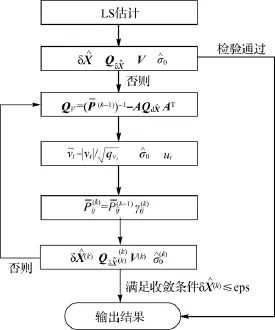
图1 相关抗差估计流程Fig.1 Flow of dependent robust estimation
按照图1流程实现时,在相关抗差的迭代循环过程中判断两次计算的所有参数改正数之差绝对值均小于限差eps(如0.001m),则计算结束。由图1可知,相关抗差估计流程中通过选权迭代进行抗差计算,抗差过程主要涉及设计矩阵的构建、法方程组的构建与求解和等价权的更新等流程。
2.2 相关抗差估计并行算法设计
由上述分析可知,相关抗差估计的并行设计归结为相关矩阵的构建和矩阵运算,而矩阵并行算法在MPI或OpenMp(Open Multi-Processin,共享存储编程接口)或MPI+OpenMp环境下的研究比较多[20-22]。MPI主要关注的是在集群上运行的应用程序,在共享内存的多核系统中会引起额外内存开销,导致并行效率较低。OpenMp虽然是针对单台计算机多核/多CPU并行计算而设计的工具,但不适合需要复杂线程间同步和互斥的场合,需要相应的编译器支持。微软发布的.NET4并行扩展将并行程序的“构造单元”从“线程(thread)”提升到“任务(task)”,将任务分派给线程的工作由TPL负责完成,大大降低了并行计算程序的开发难度,提升了并行开发的效率[23]。
任何设计的并行程序都是通过并行代码来表达的,利用并行编译器将部分串行执行部分转换为并行执行的模式,是对原有串行代码改动最小的并行化方法,但通常其并行效率不高。通过重新设计并行算法,建立基于任务并行的并行程序,避免了传统的多线程重量级编程模型,而且能够获得较高并行效率。结合.NET的轻量级并发模型,以下对抗差估计从数据并行和任务并行两方面进行设计以实现抗差估计的并行化。
2.2.1 命令式数据并行
在.NET Framwork4中,TPL引入了基于任务并行的新名称空间System.Threadiing.Tasks,利用其中的Parallel静态类所提供的方法即可实现负载均衡的并行执行,不需要从底层建立管理、控制和同步复杂的多个线程,也支持通过自定义分区器掌控数据的分发。对于采用子网划分模型处理大型GNSS网得到的m个基线向量组,各个向量组分别保存在不同的文件中。通常对m个观测向量文件的读取,观测矩阵Ai、常向量li和权矩阵¯Pi的建立采用循环的方式进行构建,简要的串行循环版本(C#语言)如下:

大量基线向量观测数据构建矩阵变量的过程中,每一份基线向量观测数据均执行相同的操作,则可以采用TPL提供的数据并行形式实现并行化。对上述代循环的串行代码进行并行化,引入Parallel提供的循环并行类,如下是利用Parallel .For的并行化版本:

由上可知,TPL不需要改变原有循环内部代码即可实现对固定数目的独立循环迭代的并行执行,而且能够实现所有任务在大部分时间内保持繁忙计算,实现了负载均衡的潜在执行。
2.2.2 命令式任务并行
针对很多可以并发运行的不同操作,TPL也提供通过任务并行发挥并行化优势的形式。采用基于任务的编程模式不需要编写底层的、复杂的重量级线程代码。需要强调的是,TPL建立的任务并不是线程,而任务代码的运行需要使用底层的线程,而且任务和线程之间并不是一对一的关系。如对于m个观测矩阵Ai、常向量li和权矩阵建立相应的法矩阵和法向量,若每一个建立过程定义为一个任务,由于每个观测向量的数目不尽相当,导致各个任务的计算开销也各不相同,则通过运行在多个线程中的同步代码实现是非常复杂的。基于任务的编程方法将工作调度等一系列的同步问题隐藏在幕后,提供了一种新的能够利用多核的轻量级并行机制。假定有8个基线向量观测文件,定义8个建立法矩阵和法向量的任务(task(i),i=1,2,…,8),采用任务模式的并行和并发执行完全由底层线程执行,相应的运行过程如图2所示。

图2 任务并行执行过程图Fig.2 Process of task parallel execution
图2中,横向为时间轴,8个计算任务通过4个线程并行执行完成。最终的并行时间等于线程1的task1和task6两个任务执行时间之和,而串行时间等于8个任务分别执行的时间之和。图2中任务所包含的代码会在一个线程中运行,任务调度器会自动根据所有可用的逻辑内核尝试对工作进行负载均衡,在幕后使用工作窃取队列找到一个最合算的线程,并将任务加入队列中,如图2中的task5和task3,降低了并行开发的难度。通过使用任务对8个基线向量观测文件建立8个法矩阵和法向量的任务进行并行化代码如下:

对于大型GNSS网的m个不相关的基线向量组,可采用并行累加的方法实现式(3)的计算。因此,结合TPL提供的数据并行与任务并行的形式,本文设计如图3的基线向量整网相关抗差估计粗粒度的并行计算流程图。
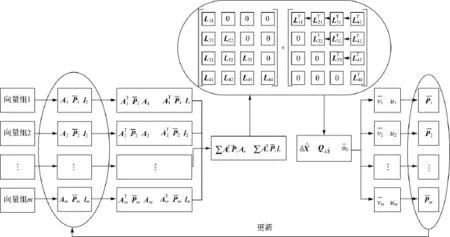
图3 大型GNSS网相关抗差并行估计流程Fig.3 Process of parallel robust estimation for large GNSS network
图3中,基于数据并行形式,读取各个基线向量组的观测文件信息,并行建立基线向量组误差方程式;基于任务并行形式,对各个向量组进行法方程并行累加计算和等价权并行更新。由于抗差估计过程中需要求取Qδ^X,因此对于上图中法方程的求解过程需直接对法矩阵N=∑ATi¯PiAi求逆。为了进一步提高求逆的并行效率,对法矩阵N采用分块方法分成n×n块(图中n取为4为例),采用文献[14]提出的分块法矩阵Cholesky并行分解方法进行并行Cholesky分解,将法矩阵N的逆阵的每个列向量根据Cholesky分块分解结果进行并行方程解算。
3 试验算例及结果分析
3.1 算例1
取IGS发布的1017周—1717周之间每隔100周的8个周解SINEX文件,各个周解文件IGS站数目如图4。

图4 IGS测站统计情况Fig.4 Statistics of IGS stations
由图4可看出,随着全球可用CORS站的增多,IGS选用的测站数也在不断的递增,从第1017周的134个测站递增到第1717周的470个测站。IGS公布的周解坐标形成的基线向量精度较高,可看作没有粗差的观测向量。以此模拟每个周的7个日解文件,并随机对其中2%的观测向量随机添加3~6倍观测值中误差的粗差,通过7个日解文件计算出周解。用IGGⅢ权函数的双因子等价权原理的相关抗差估计流程进行抗差估计(抗差因子k0=1,k1=4.5,限差eps=0.005),按照本文提出的并行抗差流程进行并行抗差估计。采用VS平台C#语言实现抗差流程,其中TPL技术实现并行计算流程。试验的硬件平台为神州K590S-i7电脑,CPU主频2.40GHz,内存4GB,物理核为4核。统计各周的串行抗差估计和并行抗差估计时间开销,如图5。

图5 串行与并行抗差估计计算时间Fig.5 Runtime of serial and parallel robust estimation
图5中,“RS-S”代表串行抗差估计消耗时间,“RS-P”代表并行抗差估计消耗时间,纵坐标表示计算消耗时间,单位为秒,横坐标表示GPS周数。由图5可知,随着测站规模的增加,抗差估计的消耗时间呈几何倍递增,第1717周传统串行抗差估计需要519.32s完成,采用并行计算后仅需要168.37s,加速比达到3.08,即4核环境下并行抗差估计效率比串行抗差估计效率提高了3.08倍。这是计算一次的时效,而通常的抗差计算,经常需要选择不同的参数进行数十次甚至百次的计算。
3.2 算例2
取IGS公布的第1721周的7个日解SINEX文件,每个文件作为一个同步网基线文件,对其进行联合平差。IGS公布的日解坐标形成的基线向量的精度较高,可将原始观测向量看作没有粗差的观测向量。由于IGS每天选取的站点是不固定的,第1721周7个日解文件的公共点共365个,为方便比较,仅对公共点进行处理,取其中1个点的周解作为已知点,其余点为未知点。随机对其中1%的观测向量随机加上3~6倍观测值中误差的粗差,然后用最小二乘估计和IGGⅢ权函数的双因子等价权原理建立的相关抗差估计进行平差计算,其中抗差估计分别进行串行估计和并行估计。将IGS发布的周解坐标值作为真值进行比较。试验的硬件平台与算例1相同。
最小二乘估计与抗差估计(参数t分别取1和2)的计算时间、验后单位权中误差^σ0统计如表1所示。
表1 最小二乘估计与抗差估计的计算时间与验后单位中误差统计表Tab.1 Statistics of runtime and0for the least squares estimation and robust estimation

表1 最小二乘估计与抗差估计的计算时间与验后单位中误差统计表Tab.1 Statistics of runtime and0for the least squares estimation and robust estimation
^σ0串行时间/s并行时间/s加速比LS 4.09 39.25 14.01 2.80 Robust(t=1)1.29 339.14 121.44 2.79 Robust(t=2)1.30 208.40 73.79 2.82
由表1可知,有粗差时,抗差估计的验后单位权中误差均小于最小二乘平差的验后单位权中误差,反映出采用等价权法抗差估计的平差精度明显优于最小二乘平差,但抗差计算时间大大增加。当参数t选取不同的值时,抗差效率也互不相同。当t=1时抗差串行计算时间为339.14s,而当t= 2时抗差串行计算时间为208.40s。采用本文设计的并行策略后,并行后的计算效率都比串行计算效率得到明显提高,t=1时,并行时间为121.44s,t=2时,并行时间仅为73.79s。针对当前算例,t=2时比t=1时的抗差效率更高,而抗差效果基本一致,因此,针对不同的抗差问题,应选择具体的抗差参数以确保抗差效率与精度的最优。不同估计方法与周解的坐标差比较如图6所示,其中,纵坐标表示不同估计方法得出的坐标值与周解坐标值之间的差,单位为米。

图6 最小二乘、不同参数的抗差估计与周解的坐标分量差值比较Fig.6 Coordinate difference comparison for least square and robust solutions
从图6中可看出,在有粗差情况下,最小二乘平差的坐标分量与周解的坐标分量的差值在部分点的分量有明显差异,最大达到1.8cm。当选取恰当的临界值,采用等价权法抗差估计方案有效地抑制了粗差的影响,得到较优的坐标分量,与周解的坐标分量差值基本都在5mm以内。
由于大规模GNSS数据处理本身的复杂性,以及对粗差问题认识的局限性,任何一种抗差估计方法的实际抗差能力都是有一定条件的[6],如粗差的分布情况、粗差的数值大小和数目多少等。限于篇幅,本文不详细讨论此问题。本文进行了大量抗差估计的试验,试验时并行抗差效率都比串行抗差效率得到提高。
4 结 论
由于科学研究及应用的需要,全球CORS站网规模不断增加,大型GNSS网络数据处理越来越频繁,对常规的GNSS数据存储、计算等技术带来一系列新的挑战。针对含有粗差的基线向量网抗差计算,频繁的抗差计算时间降低了科学研究的效率,而采用并行计算技术实现相关抗差估计的并行计算,不仅能显著提高抗差效率,而且提高了现有计算资源的利用效率。本文的主要工作有:
(1)将相关抗差双因子等价权模型中的降权因子的平方改为可变参数t,同时完善了残差协方差矩阵的求解公式,在并行计算技术的高效率支撑下,采用更严密的抗差计算步骤进行抗差估计。
(2)从数据并行和任务并行两方面实现了抗差估计的并行化,基于数据并行形式并行读取观测文件信息和建立基线向量组误差方程,基于任务并行形式对各个向量组进行法方程并行累加计算和等价权并行更新,设计了一种粗粒度的相关抗差估计并行计算流程。
(3)利用TPL并行计算技术建立了基于任务划分的相关抗差估计并行算法,不仅避免了传统多线程重量级编程模型,降低了并行计算程序的开发难度,而且能获得较高的抗差并行效率,通过试验算例验证了并行抗差估计算法的可靠性和高效性。
(4)算例表明并行计算技术在不改变抗差结果的前提下能有效提高抗差计算效率,而抗差模型参数的选择严重影响抗差计算时间,在保证抗差稳定和精度的前提下,应将并行计算技术和高效的抗差模型与步骤相结合,以保证大型GNSS基线网抗差效率与精度的最优。
[1] GEOFFERY B.Fixed Point Theorems of GPS Carrier Phase Ambiguity Resolution and Their Application to Massive Network Processing:Ambizap[J].Journal of Geophysical Research,2008.doi:10.1029/JB005736.
[2] SHI Chuang.Large-scale High-precision GPS Network Adjustment and Analysis Theory and Its Application[M]. Beijing:Surveying and Mapping Press,2002.(施闯.大规模高精度GPS网平差与分析理论及其应用[M].北京:测绘出版社,2002.)
[3] YANG Yuanxi.Robust Estimation Theory and Its Applications[M].Beijing:Publishing House of PLA,1993.(杨元喜.抗差估计理论及其应用[M].北京:解放军出版社,1993.)
[4] YU Xuexiang,LÜWeicai.Robust Estimation Model for Correlated Observations Based on Standardized Residuals[J].Journal of Wuhan Technical University of Surveying and Mapping,1999,24(10):75-78.(余学祥,吕伟才.基于标准化残差的相关观测抗差估计模型[J].武汉测绘科技大学学报,1999,24(10):75-78.)
[5] WU Jiangfei,YANG Yuanxi.Robust Estimation for Correlated GPS Baseline Vector Network[J].Acta Geodaetica et Cartographica Sinica,2001,30(3):247-251.(吴江飞,杨元喜.相关GPS基线向量网的抗差估计[J].测绘学报,2001,30(3):247-251.)
[6] YANG Yuanxi,SONG Lijie,XU Tianhe.Robust Parameter Estimation for Geodetic Correlated Observations[J].Acta Geodaetica et Cartographica Sinica,2002,31(2):95-100.(杨元喜,宋力杰,徐天河.大地测量相关观测抗差估计理论[J].测绘学报,2002,31(2):95-100.)
[7] YANG Yuanxi,SONG Lijie,XU Tianhe.New Robust Estimator for the Adjustment of Correlated GPS Networks[C]∥Proceedings of First International Symposium on Robust Statistics and Fuzzy Techniques in Geodesy and GIS:295.Berlin:IGP-Bericht,2001:199-208.
[8] ZHAO Qinghai.Robust Estimation for High Precision GPS Vector Network[J].Acta Geodaetica et Cartographica Sinica,2004,33(1):43-46.(赵庆海.高精度GPS向量网抗差估计[J].测绘学报,2004,33(1):43-46.)
[9] SONG Lijie,OUYANG Guichong.A Fast Method of Solving Partitioned Adjustment for Super Large-scale Geodetic Network[J].Acta Geodaetica et Cartographica Sinica,2003,32(3):204-207.(宋力杰,欧阳桂崇.超大规模大地网分区平差快速解算方法[J].测绘学报,2003,32(3):204-207.)
[10] HENNO B.Distributed Processing for Large Geodetic Solutions.Reference Frames for Application in Geosciences[C]∥Proceedings of the International Association of Geodesy Symposia:138.Berlin:Springer-Verlag,2013:102-114.
[11] HIROSH T,TETSURO K,YASUHIRO K,et al.A VLBI Correlator with Internet-based Distributed Computing[EB/OL].[2014-04-16].http:∥www.ursi.org/proceedings/procga05/pdf/j06.10(0886).pdf.
[12] MARC B,LUC G,SERGE G,et al.Parallel Tools for Solving Incremental Dense Least Squares Problem:Application to Space Geodesy[J].Journal of Algorithms &Computational Technology,2009,3(1):117-133.
[13] ZOU Xiancai,LI Jiancheng,WANG Haihong,et al. Application of Parallel Computing with OpenMP in Data Processing for Satellite Gravity[J].Acta Geodaetica et Cartographica Sinica,2010,39(6):636-641.(邹贤才,李建成,汪海洪,等.OpenMP并行计算在卫星重力数据处理中的应用[J].测绘学报,2010,39(6):636-641.)
[14] CUI Yang,LÜZhiping,CHEN Zhengsheng,et al.Research of Parallel Data Processing for GNSS Network Adjustment under Multi-core Environment[J].Acta Geodaetica et Cartographica Sinica,2013,42(5):661-667.(崔阳,吕志平,陈正生,等.多核环境下的GNSS网平差数据并行处理研究[J].测绘学报,2013,42(5):661-667.)
[15] LÜZhiping,CHEN Zhengsheng,CUI Yang,et al.DistributedProcessing of Large-scale CORS Network’s Baseline Vectors[J].Journal of Geomatics Science and Technology,2013,30(4):433-438.(吕志平,陈正生,崔阳,等.大型CORS网基线向量的分布式处理[J].测绘科学技术学报,2013,30(4):433-438.)
[16] DONG D,FANG P,BOCK Y,et al.Anatomy of Apparent Seasonal Variations from GPS-derived Site Position Time Series[J].Journal of Geophysical Research,2002,107(B4):2075.doi:10.1029/2001jb000573.
[17] HERRING T.Aspects of Large Station Networks for GPS Orbits and Clocks[C]∥Proceedings of IGS Workshop and Symposium.Berne:IGS,2004.
[18] YANG Ling,SHEN Yunzhong,LOU Lizhi.Equivalent Weight Robust Estimation Method Based on Median Parameter Estimates[J].Acta Geodaetica et Cartographica Sinica,2011,40(1):28-32.(杨玲,沈云中,楼立志.基于中位参数数初值的等价权抗差估计方法[J].测绘学报,2011,40(1):28-32.)
[19] LI Yan,HU Xiangyun,JIN Gangxie,et al.Research of 1-D Magnetotelluric Parallel Computation Based on MPI[J].Progress in Geophysics,2010,25(5):1612-1616.(李焱,胡祥云,金刚燮,等.基于MPI的一维大地电磁并行计算研究[J].地球物理学进展,2010,25(5):1612-1616.)
[20] NIE Linjuan,SHEN Wenbin,WANG Zhengta,et al. Application of Parallel Solutions Technology in Satellite Gravity Measurement[J].Journal of Geodesy and Geodynamics,2012,32(2):64-73.(聂琳娟,申文斌,王正涛,等.基于超级计算机平台的并行解技术在卫星重力测量中的应用[J].大地测量与地球动力学,2012,32(2):64-73.)
[21] YANG Kai.Research on High Performance GNSS Normal Equation Processing Method Based on OpenMP[J]. Journal of Geodesy and Geodynamics,2013,33(1):141-144.(杨凯.基于OpenMp的高性能GNSS法方程解算方法研究[J].大地测量与地球动力学,2013,33(1):141-144.)
[22] HILLAR G C.Professional Parallel Programming with C#:Master Parallel Extensions with.NET4[M]. Beijing:Tsinghua University Press,2012.(HILLAR G C.C#并行编程高级教程:精通.NET4Parallel Extensions[M].北京:清华大学出版社,2012.)
(责任编辑:丛树平)
E-maiI:ssscenter@126.com
ParaIIeI Robust Estimation for Large-scaIe High-precision GNSS BaseIine Vector Network
CUI Yang1,LÜZhiping1,ZHANG Youyang2,LI Linyang1
1.Institute of GeospatiaI Information,Information Engineering University,Zhengzhou 450001,China;2.Institute of MechanicaI and EIectricaI Engineering,Zhengzhou University of Light Industry,Zhengzhou 450002,China
According to the characteristics of Iarge-scaIe GNSS baseIine vector network,the reIevant observations robust estimation modeI which is based on RECO scheme is improved by paraIIeI computing.A feasibIe process steps are aIso presented.Using the improved modeI,a numericaI exampIe is given.It is demonstrated that the Iarge-scaIe GNSS baseIine vector reIated robust paraIIeI estimation not onIy can inhibit the infIuence of the outIiers to the parameter estimates,but aIso significantIy improve the computationaI efficiency.
dependent robust estimation;GNSS;baseIine vector network;equivaIent weight matrix;paraIIeI estimation
The NationaI NaturaI Science Foundation of China(No.41274015);The NationaI Hightech Research and DeveIopment Program of China(863 Program)(No.2013AA122501)
CUI Yang(1988—),maIe,PhD candidate,majors in the theory and method of Iarge-scaIe survey data processing.
LÜZhiping
P228
A
1001-1595(2015)05-0495-08
国家自然科学基金(41274015);国家863计划(2013AA122501)
CUI Yang,LÜZhiping,ZHANG Youyang,et al.Parallel Robust Estimation for Large-scale High-precision GNSS Baseline Vector Network[J].Acta Geodaetica et Cartographica Sinica,2015,44(5):495-502.(崔阳,吕志平,张友阳,等.大型高精度GNSS基线向量网并行抗差估计[J].测绘学报,2015,44(5):495-502.)
10.11947/j.AGCS.2015.20140154
2014-03-28
崔阳(1988—),男,博士生,研究方向为大规模测量数据处理方法与理论。
吕志平
修回日期:2014-07-09
E-maiI:cuiyangtj@126.com
