盘式制动器高频噪声分析*

刘志恩 张有财 杜松泽 钱 凯 袁 率 郭彩祎

(武汉理工大学现代汽车零部件技术湖北重点实验室1) 武汉 430070(武汉理工大学汽车零部件技术湖北省协同创新中心2) 武汉 430070) (欧源动力科技有限公司3) 武汉 430070)

0 引 言

汽车制动器经常在工作时发生剧烈的振动和摩擦从而发出高频的啸叫声，其频率范围可从几百至几千Hz甚至十万多Hz；声压级可达120 dB以上[1].高频噪声不仅影响人们的条件反射，使条件反射异常，更有可能影响人们的中枢神经系统，使大脑皮层的兴奋与抑制作用失去平衡[2]，因此，必须控制甚至消除制动器噪声.

制动噪声的产生机理目前主要有Sprag-Slip、模态耦合、黏-滑、摩擦-速度负斜率及锤击理论等[3-4].Jardim等[5]通过台架试验用7个大小不同的制动盘在0～50 bar的制动压力下进行的制动试验，发现制动力矩波动随着制动盘厚度波动的增加明显增大，且台架试验中的制动力矩波动及制动压力波动与道路试验中卡钳、车辆转向盘振动和踏板脉动之间有很好的相关性.张立军等[6]通过分析制动系统各部件振动特性，发现增加材料的弹性模量，系统的总体不稳定频率也在上升，弹性模量对制动系统模态耦合有着重要影响.复特征值法求解制动噪声是目前最常见和实用的方法，张礼国[7]建立盘式制动器有限元模型，利用复特征值法求解出制动器的不稳定模态及频率.王大鹏等[8-9]通过建立制动器有限元模型，对系统进行复模态分析，得到制动器系统的负阻尼比、模态参与因数、自然模态频率等，并对系统的模态应变能进行了统计.结果表明，制动片与制动盘摩擦耦合的不稳定倾向，有可能引起制动尖叫.大量的试验与研究表明，摩擦尖叫噪声频率与摩擦部件的自然频率有着很好的吻合性，基于这种现象，Rhee等[10]提出了锤击理论，指出锤击机制的本质由于制动盘自身的原因从而使制动盘受到反复的脉冲激励，这种脉冲激励会把摩擦部件的自然频率激发出来.Sinou等[11]将制动盘与制动器之间的接触刚度定义为为非线性刚度，并建立了制动器瞬态动力学有限元模型.结果表明，制动器摩擦系数与制动系统不稳定性成正比.在越来越注重汽车NVH性能的今天，制动噪声也被越来越多的汽车厂商重视，良好的制动性能及低噪声制动系统便备受青睐.

现今复特征值分析法是分析和预测制动噪声比较方便与准确的方法，复特征值模态的分析方法不仅能分析出制动器零部件之间的模态耦合对制动噪声的影响，也可分析零部件之间的物理耦合对制动噪声的影响.笔者结合模态分析理论与边界元辐射噪声法对某制动器高频噪声进行分析，研究摩擦系数与摩擦块弹性模量对制动高频噪声的影响，并对有制动啸叫倾向的制动系统进行优化，优化后系统复模态实部无正值，辐射噪声声功率级在75 dB以下.

1 理论基础

1.1 模态分析理论

汽车制动系统包含多种制动零部件，涉及到多种复杂的非线性接触，模态耦合分析得到的系统振型、固有频率和相应激励下的应力应变响应，是研究制动尖叫的起因和优化制动性能的重要参数.当不考虑系统阻尼，或者系统阻尼为比例阻尼时，此时系统产生的模态称为“实模态”.系统无阻尼和系统阻尼为比例阻尼情况下系统的模态振型是相同的.当系统阻尼不是比例阻尼时，系统模态振型就是复数值，各阶模态的自由度之间的相位关系不再是完全同相位或反相位了.这时系统产生的模态称为“复模态”.复模态分析能准确地反映系统的自然频率和振动模态，它是模态耦合机制的一个分支，近年来此种分析方法在摩擦尖叫噪声研究方面得到较为广泛使用和认可.

黏性阻尼系统振动微分方程为

(1)

式中：m，c，k分别为系统的质量、阻尼和刚度矩阵，均为N-N阶矩阵,m；k为实数对称矩阵，且m为正定矩阵.x与f分别为系统的位移响应向量和力向量，为N×1阶矩阵.

自由振动方程为

(2)

其正则形式为

(3)

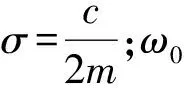
(4)

特征值λ实部代表系统的衰减系数，虚部代表系统的阻尼固有频率，当实部大于零时，表明摩擦系统是一个不稳定系统，表示有可能激励出制动尖叫.当实部小于零时，则表示系统不会出现制动尖叫.实部的大小只能表征出现振动的趋势，并不能表示最终振动幅值的大小.

1.2 边界元有限元耦合方法

边界元和有限元的耦合方法把整个求解区域分成两部分，一部分按边界元法离散，另一部分按有限元法离散.本文先求解有限元区域，然后将有限元解引入边界元区域作为边界条件，使用边界元法求解.对于先求解的有限元区域的求解方案，该区域的有限元方程为

(5)

(6)

式中：M为边界面力及其相应的等效节点力之间的转换矩阵；t0i为在界面处作用于边界元区的面力.当上式通过有限元解出作用于边界元区的面力之后，就可将其代入边界元方程为

(7)

2 某浮钳盘式制动结构及有限元模型的建立

本文研究主体为某浮钳盘式通风制动器，其总装结构见图1.研究制动盘与摩擦块之间的摩擦系数、制动盘、摩擦块材料及结构对高频噪声的影响，建立制动盘及摩擦块有限元模型，制动盘半径140 mm、厚度26.2 mm，摩擦块长114.5 mm、宽53 mm、厚17 mm.网格基本尺寸3 mm，共有节点49 715个，单元185 917个.有限元模型见图2，制动盘释放中心点沿轴向旋转自由度.摩擦块与制动盘建立接触，摩擦块释放轴向平移自由度，制动钳体之间采用equation连接方式以模拟工作时嵌体间的相对运动.制动器各部件材料见表1.

图1 盘式制动器总成

图2 有限元模型

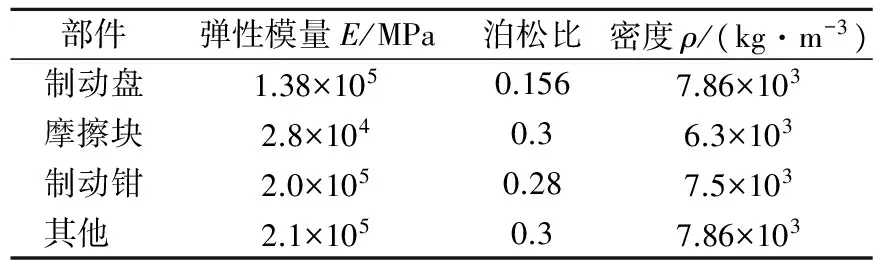
表1 单元的初始材料特性

2.1 子结构模态提取

制动啸叫噪声多为单频噪声，频率范围1 000～10 000 Hz，故此处提取摩擦块与制动盘前13 500 Hz自由模态频率，摩擦块前8阶自由模态频率见表2.

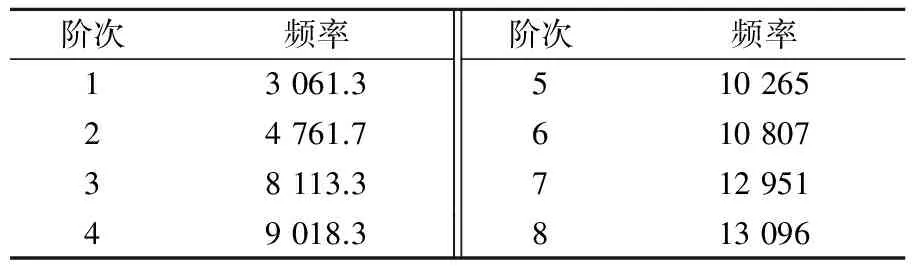
表2 摩擦块模态频率 Hz

摩擦块各阶模态振型见图3.

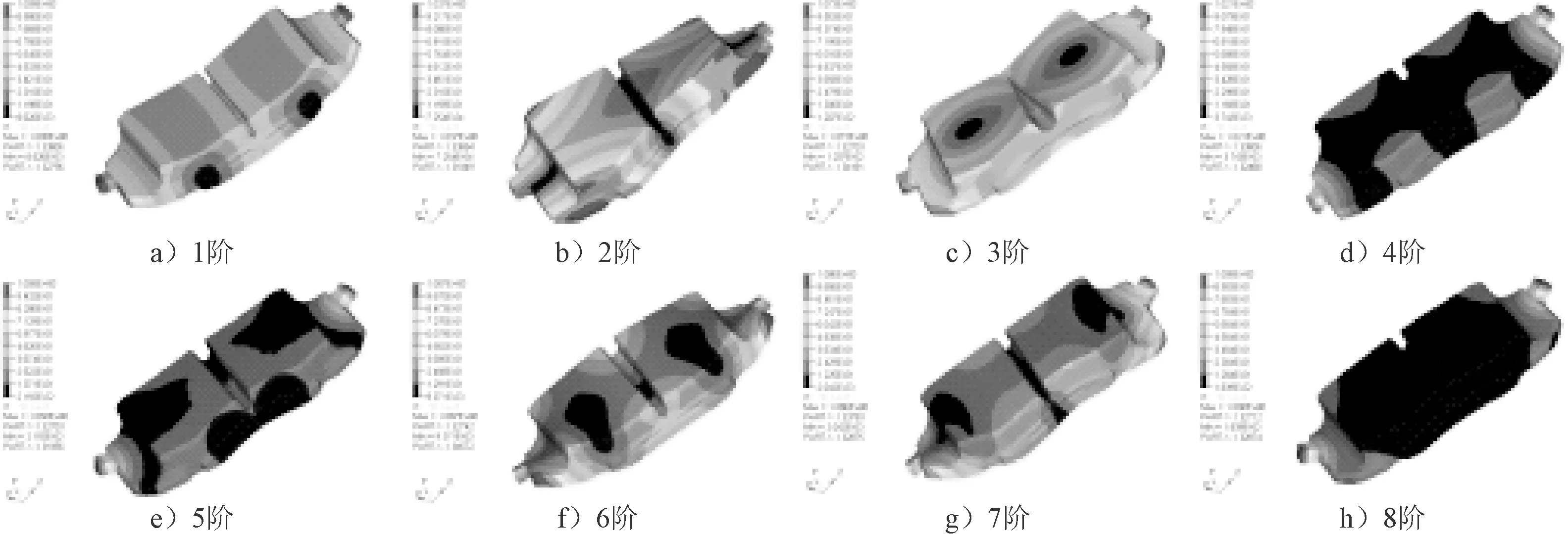
图3 摩擦块模态振型

制动盘部分自由模态频率见表3.

表3 制动盘模态频率 Hz

制动盘部分阶次模态振型见图4.

由表3可知，摩擦块固有频率在3 000 Hz以上，制动盘1阶频率也在1 000 Hz以上，而且两者也有频率十分接近的情况.这既解释了制动啸叫大多为高频噪声的原因，也验证了Rhee的锤击理论.摩擦块模态振型主要有摩擦块中部弯曲、摩擦块两端反向扭转，制动盘模态振型主要为沿轴向的弯曲振动.在实际工作过程中，摩擦块与制动盘模态耦合时有可能发生激振从而产生制动尖叫声.

2.2 耦合系统复模态分析

本文使用ABAQUS进行制动器耦合系统复模态分析，要对通风盘式制动器进行复模态分析，必要的条件是存在非对称的刚度矩阵，故在模态分析之前要先进行静力学分析，在得到摩擦块非对称应力作用和滑移刚度的基础上进行模态分析.首先制动盘与摩擦块之间定义接触和约束，制动盘只可沿中心点轴向旋转，摩擦块可沿动力方向平向移动.制动系统常在低速制动和临近停车时发生啸叫，故取制动盘转速为3.14 rad/s，给定制动压力p=3 MPa，活塞半径R=25 mm，故制动力可根据式(8)得出F=5 890 N.静力学之后再提取系统固有频(2 000～13 000 Hz)，接着提取系统的复频率(2 400～13 000 Hz).

图4 制动盘模态振型

F=π·R·R·10-6·p

(8)

2.2.1摩擦系数对复模态的影响

由于摩擦的存在，系统刚度矩阵正定性被破坏，导致系统不稳定，有产生制动啸叫的趋势.根据SAE标准，制动摩擦片生产厂商都会选用FF级额定系数，即摩擦额定系数为0.35～0.45.在实际的制动工况中，摩擦系数并不是定值，它会随着环境温度、湿度和接触面的相对运动情况等因素的变化而变化.这里为研究摩擦系数大小对制动尖叫噪声的影响，假设摩擦系数μ为定值.保持其他条件一致，改变制动盘与摩擦块间的摩擦系数，分别取摩擦系数0.3,0.35,0.4,0.45,0.5，系统复模态实部值分布情况见图5.

由图5可知，μ=0.3时，系统复模态实部值没有正值，表明系统为稳定系统，将不会产生制动啸叫；μ=0.35时，系统复模态实部共出现3处正值，α值最大为37，表明系统在该对应频率处不稳定，可能出现制动啸叫；μ=0.4时，系统复模态实部共出现4处正值，α值最大为49；μ=0.45时，系统复模态实部共出现8处正值，α值最大为145；μ=0.5时，系统复模态实部共出现8处正值，α值最大达182.随着摩擦系数的增大，系统出现不稳定频率的概率增大，复模态实部值α值也呈增大趋势，发生制动啸叫的概率也越大.

图5 不同摩擦系数下系统复模态实部值

2.2.2制动盘材料对复模态的影响

保持其他参数一样，只改变摩擦块弹性模量，研究摩擦块弹性模量对系统复模态的影响，取摩擦块弹性模量E=1 300，28 000，138 000 MPa，分别代表石棉摩擦材料、半金属摩擦材料和灰口铸铁型摩擦材料这三种在汽车制动系统中应用较多的摩擦材料弹性模量水平.系统复模态实部值分布情况见图6.

由图6可知，摩擦块弹性模量E=1 300 MPa时，系统复模态实部共出现6处正值，α值最大为100，表明系统在该对应频率处不稳定，可能出现制动啸叫；摩擦块弹性模量E=28 000 MPa时，系统复模态实部共出现4处正值，α值最大为89；摩擦块弹性模量E=138 000 MPa时，系统复模态实部共出现3处正值，α值最大为45.随着摩擦块弹性模量的增大，系统复模态实部出现正值的概率越来越小，实部值α的值也呈减少趋势，表明系统稳定性越来越好，发生制动啸叫的概率也减少.

图6 不同摩擦块弹性模量下系统复模态实部值

2.3 辐射噪声计算

以系统复模态结果作为振动源，导入LMS Virtual.Lab中计算系统的辐射噪声，算得不同摩擦系数和不同摩擦块弹性模量下系统的辐射噪声，研究摩擦系数与摩擦块弹性模量对制动高频噪声的影响.辐射噪声模型由结构有限元模型、声学边界元模型和外声场三部分组成.结构有限元模型的节点振动数据通过数据转移映射到声学边界元模型，本次数据转移的方法是在声学边界元网格某一节点半径10 mm的圆范围内寻找最多4个结构网格上的节点作为该声学网格节点的原始数据，目标节点的值由源节点的值确定，具体公式为

(9)

图7 数据转移示意图

图8 辐射噪声模型

2.3.1摩擦系数对辐射噪声的影响

依然取摩擦系数0.3，0.35，0.4，0.45，0.5，系统辐射声功率级见图9.

图9 不同摩擦系数下系统辐射声功率级

由图9可知，μ=0.3时，整个频域内声功率级不超过70 dB，系统较为安静；μ=0.35时系统声功率级在7 500 Hz附近出现峰值，表明在该频率处出现啸叫，声功率级幅值达90 dB；μ=0.4时系统声功率级在7 100～7 800 Hz接近90 dB，在8 100 Hz和9 400 Hz出现峰值；μ=0.45时总体情况与μ=0.4接近；μ=0.5时，啸叫主要集中在1 000～1 100 Hz之间，声功率级幅值最高达100 dB.

2.3.2制动盘材料对辐射噪声的影响

同样取摩擦块弹性模量E=1 300，28 000，138 000 MPa，系统辐射声功率级见图10.

由图10可知，摩擦块弹性模量E=1 300 MPa时，系统声功率级在9 800 Hz和10 400 Hz处出现明显的峰值，声功率级最大可达90 dB；摩擦块弹性模量E=28 000 MPa时，声功率级只出现一处峰值，声功率级幅值下降5 dB；摩擦块弹性模量E=138 000 MPa时，声功率级只在1 150 Hz处出现峰值，其余频域内幅值在70 dB以下.表明随着摩擦块弹性模量的增大，制动器辐射啸叫发生概率越来越低，系统越安静.

图10 不同摩擦块弹性模量下系统辐射声功率级

3 抑制尖叫的措施

通过以上分析结果，可知从两个方向改善或消除制动系统尖叫声，即摩擦系数和材料的弹性模量.对于摩擦系数，大量的试验研究发现，不存在摩擦噪声的地方与存在摩擦噪声的地方磨痕形貌有较大的差别，不存在摩擦噪声的地方磨痕的表面粗糙度较小，相对比较光滑，存在摩擦噪声的地方磨痕的表面的粗糙度较大，相对比较粗糙，而摩擦系数较大的地方，表面粗糙度较大，摩擦力变化更为剧烈，从而更容易激发出摩擦噪声.因此适量降低摩擦系数降低产生制动尖叫噪声的可能性的同时.不过，虽然降低摩擦系数可减小产生制动尖叫噪声发生的可能，但过小的摩擦系数又是车辆安全运行所不允许的，因此要统筹考虑行车安全与减振降噪.

对于弹性模量，它是材料对弹性变形的抗力，即材料发生弹性变形的难易程度，代表了材料的刚度.分析结果表明制动块弹性模量越大，系统发生制动啸叫的可能性越低，辐射声功率级越低，系统较为安静.对于灰铸铁而言，可通过加入Sn,Cr,Cu,Ni等金属元素微合金化，优化孕育量和孕育工艺，改善石墨形态，细化共晶团等措施来增加其弹性模量.通过合理地优化零件的结构和刚度，可以有效降低制动噪声甚至消除制动尖叫.综合以上结果分析，将摩擦块槽深减少3 mm，与制动盘接触面外沿倒角由1 mm改为2.8 mm，对比前后制动系统的复模态结果及辐射噪声结果.摩擦块结构改进前后见图11.

图11 摩擦块结构改进前后对比

改进前后系统复模态结果及辐射噪声结果见图12和图13.

图12 系统复模态实部值

图13 系统辐射声功率级

由图12～13可知，结构改进前系统出现六个不稳定模态，这六个不稳定模态都在7 000 Hz以后，系统的辐射噪声也在7 500，8 300，9 300，10 500，13 400 Hz处出现明显峰值，这几处声功率级幅值均在88 dB以上，最大达100 dB.结构改进后复模态实部无正值出现，辐射噪声声功率级在整个分析频域都比较均匀，最大声功率级不超过75 dB，制动系统处于较安静状态，表明改进方案切实可行.

4 结 论

1) 摩擦系数和摩擦块弹性模量对制动系统高频噪声有重要影响，系统摩擦系数越大，复特征值实部出现正值的概率越大，值的大小也越大，则容易出现啸叫；摩擦块弹性模量越大，复特征值实部出现正值的概率越小，则不容易出现啸叫.

2) 从消除啸叫角度看，摩擦系数应尽量小，但过小的摩擦系数会对行车安全造成安全隐患，因此系统摩擦系数不可过小，一般控制在0.35～0.45之间.摩擦块弹性模量越大，其刚度也越大，系统不易出现啸叫.增加其弹性模量等效于提高其刚度，故可从提高系统的刚度抑制啸叫.

3) 系统复模态实部出现正值频率处辐射噪声声功率值出现峰值，且值越大，声功率值也越大，最大可达100 dB.复模态结果与辐射噪声声功率结果的高吻合度说明仿真结果真实可靠.

[1] 黄学文,张金换,董光能,等.汽车摩擦制动噪声研究进展与发展趋势[J].汽车工程,2007,29(5):385-388.

[2] 徐国勇,黎丽春.某汽车制造厂噪声危害特征分析[J].中国卫生工程学,2014,13(3):218-224.

[3] 王冀军,陈光雄.接触共振频率与摩擦噪声频率之间关系的试验研究[J].摩擦学学报,2014,34(3)：278-284．

[4] 管迪华,宿新东.制动振动噪声研究的回顾 发展与评述[J].工程力学,2004,21(4)：150-155.

[5] JARDIM F B, TAMAGNA A. Study of the relationship between DTV, BTV and BPV over judder-type vibration of disc brake systems[J]. Sae Technical Papers,2010,38(6):4125-4135.

[6] 张立军,唐传骏.制动盘弹性模量对制动尖叫影响的仿真分析[J].汽车工程学报,2013,3(5)：313-323.

[7] 张礼国.制动块参数对盘式制动器制动尖叫的影响研究[D].北京：清华大学,2014.

[8] 王大鹏.盘式制动器制动噪声分析与研究[D].石家庄：河北科技大学,2012.

[9] GUAN D H, HUANG J C. The method of feed-in energy on disc brake squeal[J]. Journal of Sound and Vibration,2003,261(2):297-307.

[10] RHEE S K, TSANG P H S, WANG Y S. Friction-induced noise and vibration of disc brakes[J]. Wear,1989,133(1):39-45.

[11] SINOU J J, COUDEYRAS N, NACIVET S. Study of the nonlinear stationary dynamic of single and multi-instabilities for disk brake squeal[J]. International Journal of Vehicle Design,2009,51(2):207-222.