一种舰船轴系滑动轴承阻抗的建模方法*

2018-05-02崔海超熊义勇

武汉理工大学学报（交通科学与工程版） 2018年2期

嵇斗崔海超熊义勇李洋

(海军工程大学电气工程学院1) 武汉 430033)(海军工程大学舰船综合电力技术国防科技重点实验室2) 武汉 430033) (91315部队3) 大连 116041)

0 引言

舰船腐蚀相关电场中，舰船的轴频电场因其信号特征明显、容易被远程侦测，受到了广泛的关注[1-2].目前对于舰船轴频电场的建模基本上采用电偶极子和时谐电流元的方法[3]，不能反映其产生的机理.如果在一定条件下，把来源复杂并且影响舰船水下电场分布的主要因素理想化为简单的电路元件，建立一种直观简单便于分析的等效电路模型，对于研究舰船水下轴频电场具有重要意义.对于舰船轴频电流等效电路的建模，在公开发表的国内外文献中研究较少，加拿大Davis公司在其网站宣传页面中给出了一个简单的轴电流回路[4]，文献[5]对滚动轴承的轴电流回路进行了建模，对于多采用滑动轴承的舰船轴系并不合适.对于舰船轴电流等效电路的建模，滑动轴承的接触阻抗研究是其关键，文献[6-7]定性的分析了轴承接触电阻在轴频电流形成过程中所起的作用以及接触压力与接触电阻之间的关系，未给出用于计算和建模的接触阻抗模型.本文以滑动轴承的振动为基础，建立了一种滑动轴承接触阻抗等效电路模型.

1 舰船轴频电流的产生

位于水下的舰船船壳和各种装置是由不同的金属材料制作而成，这些不同的金属材料形成的部件浸入海水中时，由于海水良好的电解质作用，会形成不同的电位分布在船体表面，形成电化学腐蚀，加快了舰船在海水中的腐蚀速度，对于舰船的防护极为不利.舰船的电化学腐蚀会产生腐蚀电流，在不同电位的金属之间构成回路，形成了舰船的腐蚀相关电场.当铜质的螺旋桨与舰船船壳水下裸露金属部位存在电位差时，腐蚀电流一般由裸露的金属部位经海水流向螺旋桨，然后由螺旋桨通过舰船的推进轴系、传动装置、轴承等装置流回到船壳水下裸露的金属部位，当螺旋桨不转动时，该回路产生的电流基本不发生变化，形成舰船的腐蚀静电场，当螺旋桨旋转时，螺旋桨轴系的电接触阻抗，在螺旋桨的旋转振动下发生周期性的变化，形成舰船不加防腐和电场防护装置的轴频电流，产生轴频电场.

2 滑动轴承振动模型

轴承作为舰船上的一种连接和支撑装置，是舰船上各种机械装置的重要组成部分.以在运转过程中受到的摩擦力大小可以将轴承分为滑动轴承和滚动轴承两种，目前舰船推进轴系一般采用滑动轴承.在舰船的实际航行过程中，舰船整个轴系会发生耦合振动，诸如螺旋桨桨叶的叶倍频振动、减速齿轮箱的耦合振动及主轴的基频和倍频振动等.分析舰船滑动轴承的润滑油膜的工作原理可知，滑动轴承油膜力形成的收敛楔产生的支撑力的方向与滑动轴承所受载荷的方向会有一个夹角，此力是形成舰船滑动轴承周期性振动的根源[8-9].

采用无限短的滑动轴承模型进行建模，假设轴颈质量分布均匀，对于一个非线性转子-轴承系统，考虑其有两个自由度的稳态周期，将湍流的影响计入其中使用湍流润滑系数对雷诺方程加以改进.本模型采用直角坐标系，对舰船滑动轴承的非线性油膜力进行分析计算，此模型在直角坐标系中的力学模型见图1.

图1 转子-轴承系统力学模型

由图1可知，此模型为一个对称性的结构，其量纲一的量的运动微分方程为

x″=fx(x,x′,y,y′,k)/m+ρsin(kτ)

y″=G+fy(x,x′,y,y′,k)/m+ρcos(kτ)

(1)

(2)

以实验室某滑动轴承的参数为例，mR=106 kg；R=79 mm；c=1 mm；L=99.6 mm；η=17.8×10-3Pa·s；润滑油密度为0.88×103kg/m3；e和ω为参变量.

由式(1)～(2)可知，滑动轴承的量纲一的量运动方程是一个二阶非线性微分方程，对其进行解析求解难度较大，本文主要将式(1) 两个二阶微分方程转化为四个一阶微分方程，通过Matlab采用龙格-库塔算法对四个一阶方程组进行数值积分求解.可得到轴颈在不同转速下的振动轨迹见图2.

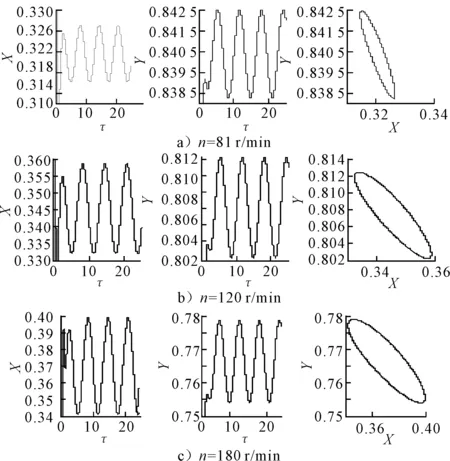
图2 不同转速下滑动轴承的振动轨迹

舰船推进轴系轴径旋转速度相对较小，一般会产生同步振动并伴随有相应的倍频出现[10]，故对无量纲微分方程k>1时的亚谐解不进行过多研究.由图2可知，舰船滑动轴承轴颈在发生同步振动时，滑动轴承的轴心轨迹为一个椭圆并且在一定的转速范围内随着转速的增大，振动增强.根据文献[11]求解滑动轴承振动轨迹近似解析式的过程可以看出，式(1)的特征函数为三角函数，以81 r/min为例结合图2的振动轨迹，不妨设无量纲坐标x、y为

(3)

3 滑动轴承阻抗的推导与建模

舰船在海上航行过程中，其轴电流回路中轴系部件的联通大部分为旋转的电接触，例如，尾轴前后轴承与主轴的接触、推力轴承与主轴的接触、其他机械部件与主轴的接触等都是电接触，在轴系振动过程中，电接触的面积及压力发生的周期性变化导致产生周期性变化的电阻，这是产生轴频电流的根源所在.当在舰船推进轴系的轴颈上加上轴接地的电刷时，其轴频电流明显增大，说明轴颈与电刷的接触电阻也不可忽略，滑动轴承轴颈与电刷的接触见图3.

图3 滑动轴承轴径与电刷接触结构

电接触电阻通常由收缩电阻Rc和表面膜电阻Rf组成，其一般表达式为

(4)

式中：a为凸丘半径；ρ为接触面两种物质的平均电阻率；α为相互电阻的霍姆半径或点集半径[12]；ζ为膜的隧道电阻率.

在实际的工程中接触电阻接触面粗糙情况非常复杂，其中影响其接触的各种因素非常之多，在理论上没有一种精确的模型，格林渥和威灵逊假定[13]，接触表面的凸丘服从指数分布或是高斯分布，在实验过程中发现，对于大多数接触表面来说，实际情况更倾向于高斯分布.结合图3和式(3)以及τ=ωt可知轴径沿右侧和左侧电刷方向量纲一的量振动量h1和h2分别为

h1=(x-0.320 6)cos 45°-

(y-0.840 3)cos 45°

h2=-(x-0.320 6)cos 45°-

(y-0.840 3)cos 45°

(5)

以上述提到的滑动轴承参数为例，假定电刷表面的凸丘均匀分布服从高斯分布，各凸丘之间相互独立，凸丘密度β=3 000个/mm2，各凸丘半径相同，a=1 nm,电刷的接触面积S=2 cm2，膜的隧道电阻率σ=5×10-13Ω·m2，电阻率ρ=9.78×10-8Ω·m[14]，则右侧电刷与轴径的接触电阻为见式(6)，在不同高斯分布下右侧电刷的接触电阻图见图4.

(6)

式中：γ，μ为高斯分布的方差和期望.

同理可得左侧电刷与轴径的接触电阻Rj2.

图4 在不同高斯分布下右侧电刷的接触电阻

对于轴瓦与轴颈的接触，由于接触表面的粗糙程度难以掌握，凸丘的个数和大小计算非常困难，故使用工程经验公式计算接触表面的电阻.

(7)

式中：f为接触压力；m为与接触形式、压力范围和实际接触点的数目等因素有关的指数；kj为与接触材料、表面状况等有关的系数.结合文献[14]中给出的公式参数表，取kj=0.3，m=0.5，根据式(3)、式(7)，以及量纲一的量油膜力与油膜力之间的关系可得轴瓦与轴颈的接触电阻，见图5.

图5 轴颈与轴瓦之间的接触电阻

对于滑动轴承轴瓦与轴颈之间的等效电容可等效为非平板电容器模型，见图6.其电容的表达式为

(8)

式中：hmin为滑动轴承的最小油膜厚度；hmax为滑动轴承的最大油膜厚度,极板的长度为L，极板的宽度为2πR.

图6 滑动轴承等效电容模型

模型中θ非常小，故

(9)

考虑到滑动轴承的振动，求解滑动轴承的等效电容主要是轴颈沿轴瓦中心振动量的确定，根据式(3)所给出的滑动轴承在横向和纵向的无量纲振动方程的解析式可推导得出，轴颈沿轴承中心振动的振幅H为

(10)

滑动轴承的最小油膜厚度等于半径间隙减去轴颈沿轴承中心振动的振幅，即

hmin=c-H

(11)

由式(11)推导可得

hmax=2r-2R-hmin=c+H

(12)

根据求得的滑动轴承的最小油膜厚度和最大油膜厚度，即可计算得出夹角θ，然后将其和式(11)带入式(8)即可求得滑动轴承的等效电容，见图7.

图7 轴颈与轴瓦之间的等效电容

4 轴电流仿真结果与实船轴电流对比

根据滑动轴承的结构可知，轴颈与电刷之间的接触电阻Rj1，Rj2和轴颈与轴瓦之间的接触电阻Rj3以及轴颈与轴瓦之间的容抗jωCA四者之间是并联关系,见图8.

图8 滑动轴承阻抗等效电路

若在滑动轴承两端加以10 mv的电压，结合上文所得的电路参数以及欧姆定律可得滑动轴承在不同高斯分布下的轴电流见图9，其频谱见图10.

图9 不同高斯分布下的轴电流

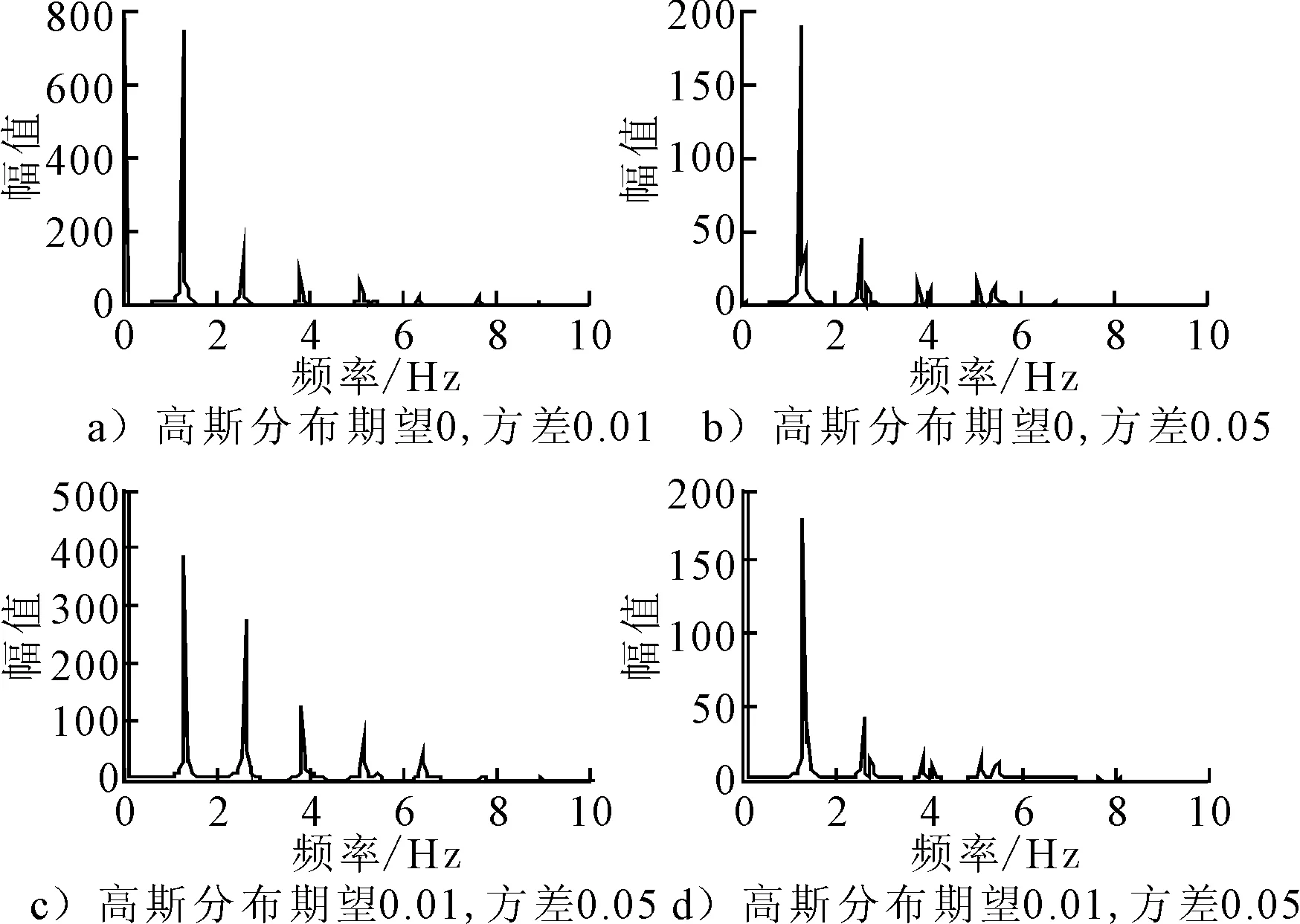
图10 在不同高斯分布下的轴电流频谱

由图9～10可知，对于电刷表面凸丘高斯分布在不同的期望和方差下，其轴电流的变化和频谱是有差异的，对于期望和方差的选择需要根据具体的滑动轴承和电刷通过大量的实验来确定.

通过对某船螺旋桨在81 r/min时轴电流的测量，得到了该船右轴电流的实测数据及轴电流的频谱图，见图11.选择滑动轴承接触阻抗等效电路在高斯分布期望0.01方差0.01的情况下与实船右轴电流进行对比，见图12.

图11 某船右轴电流频谱

图12 仿真结果与某实船右轴电流的对比

由图11～12可知，所建模型得到的轴电流与实船轴电流达到了比较好的吻合，并且频谱在基频及其倍频上也达到了一定的吻合.

5 结束语

本文对滑动轴承阻抗的等效电路进行了建模和仿真，结果表明，产生的轴频电流以滑动轴承的旋转频率为基频，同时伴有相应的倍频出现，其与实船轴电流的对比达到了一定程度的吻合，证明该建模方法在理论上的可行性.但是，舰船整个轴系旋转耦合振动非常复杂，诸如螺旋桨浆叶的叶倍频振动、减速齿轮箱的咬合振动等，都会影响轴频电流的大小和频率成分，关于这方面的分析建模还有待于进一步研究.

[1] 卢新城,王婷,陈新刚,等.海船轴频电场建模方法研究[J].武汉理工大学学报(交通科学与工程版)，2012,36(1)：168-170.

[2] 卢新城,龚沈光,孙明.舰船轴频电场空间分布特性的实验测量与分析[J].武汉理工大学学报(交通科学与工程版)，2004,28(4)：498-500.

[3] 朱武兵,嵇斗,王向军,等.浅海中四桨运动舰船产生的轴频轴频电磁场[J].舰船科学技术，2014,36(1)：34-37.

[4] KOICH.Wrdavis company[EB/OL].http://www.wrdavis.com.2014-01-18．

[5] 曹寓.基于等效分析的舰船轴电流电路模型研究[D].武汉：海军工程大学，2014.

[6] 蒋培.轴频电场中接触电阻的实验研究[J].武汉理工大学学报(交通科学与工程版)，2014，38(6)：1291-1294.

[7] 姬庆.舰船轴频电场中的接触电阻研究[J]．四川兵工学报，2014，35(8)：127-130．

[8] 沈小要.转子-轴承-密封系统非线性动力学理论和试验研究[J].噪声与振动控制，2009(6)：67-71.

[9] 杨金福.滑动轴承轴径涡动机理的非线性特性研究[J].动力工程，2005，25：562-568.

[10] 张新勇.滑动轴承油膜涡动及油膜振荡研究[J].太原理工大学学报，2008(3)：232-235.

[11] 陈予恕.非线性转子-轴承系统的分叉[J].振动工程学报，1996(3)：266-275.

[12] HOLM R. Electrical contacts[M].New York: Springer,1979.