基于航空器滑出时间的离场影响因素研究*

刘继新 尹旻嘉 朱学华 曾逍宇

(南京航空航天大学民航学院 南京 211106)

0 引 言

航空器滑出时间是指航空器从推出到起飞的时间段内，包括滑行道上的滑行时间和离场排队时间，直观地反应了机场场面的运行效率.

确定影响离场活动的因素的关键在于如何正确建立数学模型拟合滑出时间.Idris等[1]基于多元线性回归方法和波士顿里根国际机场的数据，第一次强调了在预测滑出时间时考虑到地面上的当前交通量的重要性，发现离场队列的长短是滑出时间的一个特别重要的解释变量.Regina等[2]通过对里根机场和肯尼迪机场的数据进行分析和比较，拟合滑出时间与各因素的函数关系来预测滑出时间.Balakrishna等[3-4]使用了强化学习算法，得出的模型在底特律国际机场和坦帕国际机场显示出良好的结果.Jordan等[5]反向探究，选取达拉斯沃斯堡机场的数据，提出了一个从多种相关变量中选取出最不相关的变量研究方法.欧洲研究学者则认为美国机场与欧洲机场在结构和管制程序上不一致，认为在美国的滑出时间预测的问题由跑道队列大小主导，并且与飞机必须滑行的实际距离相关性较小[6]，这与欧洲的实际情况有所区别.国内目前关于滑出时间的研究较少，冯霞等[7]通过分析进离港航班流量、跑道分配、滑行距离及其他随机因素等与滑出时间的相关性，提出以航空器滑出期间使用同一条跑道离港和进港的航班数量来衡量场面交通状况，证明了其有效性并建立了基于该指标的无障碍滑出时间计算模型.其他相关研究主要集中在对滑行路径的优化[8-9]等场面优化策略.这些研究并没有深入讨论模型的有效性，例如，没有经过交叉验证，难以评价一些发现的准确性和重要性.

本文提出了基于滑出时间的分析方法，并以H机场为例，结合中国实际情况，采用较为详尽的数据集和严格的统计工具，通过分析原始数据，提出数学拟合模型，分析滑出时间的变化趋势，通过与实际运行数据的反复拟合、比对，得出较为客观的影响规律，最终构建较为全面准确的滑出时间解释模型，并对离场运行优化提出建议.

1 滑出时间影响因素分析

1.1 滑出时间影响因素探究

研究机场场面滑出时间解释模型最重要的是如何定义航空器的滑出时间，FAA对滑出时间的定义为：飞机从推出停机位到起飞离地过程的时间.以此为基础，本文认为航空器的滑出时间是指航空器从推出到起飞的时间段，包括滑行道上的滑行时间和离场排队时间.本文研究的重点参数为滑出时间T.

T=tATOT-tAOBT

(1)

式中：tATOT为航班实际起飞时间；tAOBT为航班实际撤轮档时间.

离场航空器滑行运行的主要因素，包括进离场航空器数量、跑道构型、天气和运行时段等.此外，还发现对于离场滑行时间的影响还取决于该机场跑道运行方式，因为随着进离场跑道之间冲突的增加，滑出时间也会随之增长.

选取的H机场整体构型见图1，这也是目前中国大部分机场所采用的机场构型，运行模式采用隔离运行模式，即一条跑道用于起飞，一条跑道用于降落，进离场跑道之间不存在交叉冲突问题，所以本文不研究跑道运行方式对滑出时间的影响.

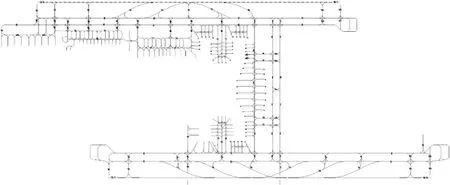
图1 常见双跑道机场平面构型图

结合现有的航班历史数据及文献[10]，得出本文主要研究的影响因素：

1) 空管原因(包括流量控制) 由于空域有限或军航活动，流量控制常常发生，最常见的办法就是指挥航空器在地面等待，这样做可能会使航空器排队等待时间增长从而增加滑出时间.

2) 天气原因 风速、能见度等以影响航空器的滑行速度来影响滑行时间.

3) 航空公司原因 在实际数据中由于航空公司造成的航班延误也占一定比例.

4) 旅客原因 由于旅客突发状况也会引起航班延误现象.

5) 同时段进离场航班数量 由于机场跑道、滑行道、机坪等资源有限，在航空器滑出期间进场或离场的航空器会彼此产生影响从而增加滑出时间.

6) 机场运行时段 由于不同的时间段导致的场面拥堵程度不同，滑出时间也由此增加.

1.2 各因素与滑出时间相关性研究

首先对提出的影响因素进行相关性检验，初步判断与滑出时间的相互关系，将相关性较低的变量剔除，减少无关变量对模型的影响.本文使用H机场7—9月的航班历史运行数据进行研究，滑出时间最大值为33 min，最小值为2 min，平均值为15 min，中值为14 min，利用spss17.0软件计算Pearson系数[11]，结果见表1.

表1 各影响因素相关性分析

注：*-在 0.05 水平(双侧)上显著相关;**-在 0.01 水平(双侧)上显著相关.

Pearson相关系数的绝对值越大，表示相关性越强：相关系数越接近1或-1，相关性越强，相关系数越接近到0，相关性越弱.对滑出时间T与空管、天气、航空公司、旅客、同时段进离场航班数量和运行时段进行相关性分析，得到相关性系数和实际显著性水平如表1所示.通过分析不难发现，同时段进离场航班数量Pearson相关性系数为0.623，表示其与滑出时间T之间存在强相关，且实际的显著性水平为0.004，低于0.01的理论水平，说明相关系数的值不是由偶然因素造成的，即同时段进离场航班数量和滑出时间T之间是高度线性正相关.同样的，运行时段也与滑出时间T高度相关.而其他变量的Pearson相关系数全部都小于0.2，显著性水平小于0.05，说明其他的变量与滑出时间T之间存在弱相关关系，即除同时段进离港航班数量和运行时段作为解释变量会引起滑出时间的变化外，其他因素的影响可忽略不计.

2 滑出时间解释模型的建立

2.1 定义关键变量

2.1.1离场航班数量

要建立一个较准确的滑出时间解释模型，主要研究离场航空器数量、进场航空数量与滑出时间的相关性，关键性在于如何对离场航班和进场航班进行定义，现通过对机场初始数据的分析，给出如下初始的离场航班为

tAOBT(j)tAOBT(i) (2)

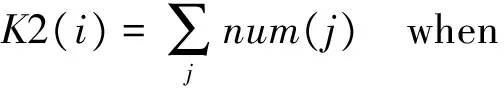
tATOT(j)tAOBT(i) (3)

式(2)表示所有在航空器i推出时所有已推出但未起飞的离场航空器数量；式(3)表示在i航空器滑出过程中所有起飞航空器数量.

2.1.2进场航班数量

与离场航班相比，进场航班对离场滑行的影响的定量研究较少.本文对进场航班数量进行了多种定义，为

tAIBT(j)>tAOBT(i)>tATOT(j)

(4)

tAOBT(i)

(5)

tAOBT(i)

(6)

tAOBT(i)

tAOBT(i)

(7)

与离场情况相同，式(4)表航空器i推出时已经着陆但未进入机位的进场航班数量；式(5)表示航空器i在滑行过程中降落的航班数量.式(6)表示航空器i在滑行过程中滑入机位的进场航空器数量；式(7)表示航空器i滑行过程中着陆并进入机位的进场航空器数量.

2.1.3运行时段

通过对机场历史航班运行数据进行分析，统计各时间段延误时长，得到延误时长分布规律，将延误时长进行K-means聚类[12]，经过多次聚类实验，根据K-means聚类后根据延误率变化趋势，将全天24 h划分不同的运行时段，进而研究运行时段对滑出时间的影响.

2.2 滑出时间解释模型

回归分析是在已知的某组数据下，通过最小二乘法将这一组数据拟合为线性相关的一条曲线的过程，设随机变量y与一般变量x1,x2,…,xk的线性回归模型为

y=β0+β1x1+β2x2+…+βkxk+ε

(7)

式中：β1,β2,…,βk为k+1个未知参数；β0为回归常数；β1,β2,…,βk为回归系数；y为被解释变量；x1,x2,…,xk是k个可以精确可控制的一般变量，称为解释变量；ε为误差.

多元线性样本回归方程为

(8)

在多元线性回归方程中，对回归系数的估计也可用最小二乘法来确定.由残差平方和:

(9)

根据微积分中求极小值得原理，可知残差平方和SSE存在极小值.欲使SSE达到最小，则SSE对的β0,β1,β2,…,βk偏导数必须为零.

将SSE对β0,β1,β2,…,βk求偏导数，并令其等于0，加以整理后可得到k+1个方程式

(10)

(11)

基于以上理论，根据选取的关键变量假设滑出时间回归的模型，并对建立的解释模型进行检验[13]评估是否能用于进行下一步研究，若模型不符合要求，则需调整模型，直至模型各项参数符合要求.

3 滑出时间解释模型建立及评估

3.1 关键变量的选取

对H机场2015年7-9月份共26 170数据进行处理，得到25 856条可用于回归分析的数据.首先对数值型变量进行相关性分析，得到结果见表2.

表2 相关系数矩阵

由表2可知，所有变量之间都存在显著的相关性，其中被解释变量T与K3呈现微弱的负相关性，与其他解释变量均呈现正相关性.由上表我们可以确定K3，K1与滑出时间之间相关性极弱，在建立滑出时间解释模型时不考虑此二种因素，因此不考虑K3及K1与其他解释变量之间的相关性可能会导致回归中存在变量间的共线性.

另外，K4与K5间存在较强的正相关性，相关系数为0.858，这一解释变量间的相关性可能会导致回归中存在变量间的共线性，进而影响回归结果，为此，我们要在回归中观测模型的共线性统计量，避免伪回归.

3.2 运行时段的选取

通过对机场历史航班运行数据进行分析，将延误时长进行K-means聚类，经过多次聚类实验，根据延误率变化趋势，将全天24 h划分成4个时间段，迭代12次，运行时间段划分结果见表3.结果显示，延误率有规律可循，运行时段周期性变化尤为突出.

表3 航班延误率划分

00:00-07:59航班量较少，因此不予考虑.所以将机场1 d的运行时段分为三段，分别为T1(08:00-13:59)，T2(14:00-20:59)，T3(21:00-23:59)，以此来反应场面拥堵情况.

3.3 模型的建立与检验

3.3.1模型假设

根据选取的关键变量及模型建立条件，可以假设滑出时间回归模型为

式中：C为回归方程常数项；βi为回归系数；ε为回归误差.进场航班数与离场航班数为数值型变量，运行时段为字符型变量.

3.3.2模型检验

对建立的解释模型需要进行检验才能评估是否能用于进行下一步研究.观察回归的残差分布直方图和残差正态概率图，图2为未标准化残差的正态概率图.

图2 未标准化残差的正态概率图

图2中的点基本都在直线上方或下方附近，说明了变量之间是呈线性分布的，因此，回归模型满足正态性假设，残差分布近似沿一条直线.同时在残差正态概率图中可以发现，标准化残差沿一条正态曲线分布.由此可以推断，回归方程满足线性以及方差齐次的检验，即数据不存在异方差性，回归模型的结果是可靠的.

1) 多重共线性检验

由于变量之间具有相关性对拟合结果不利，因此需要对数据进行共线性诊断，数据的共线性诊断结果见表4.

表4 共线性统计量

正常情况下，当某个变量的VIF(方差膨胀因子)大于10或者容差小于0.1，可以得出数据之间有多重共线性的结论，当VIF>100或容差小于0.01，表明变量之间存在着严重的多重共线性.通过分析表4，可以得出以下结论：模型不存在多重共线性.

2) F值检验

对回归方程进行显著性检验，实质上就是检验被解释变量与所有解释变量之间以及各解释变量之间的线性关系是否显著.对回归方程进行显著性检验即要看解释变量X0,X1,…,Xp从整体上对随机变量Y是否有明显的影响，显著性检验有两种方法：一是对回归方程显著性的F检验，二是对回归系数显著性的t检验.这里仅对F检验进行论述，t检验原理相同.使用F统计量作为检验统计量，使用F统计量作为检验统计量，选定显著性水平α=0.05，利用SPSS软件计算出的方差可知，解释模型显著性P值为0.000，即Sig值小于0.05，因此拒绝原假设，即回归方程通过显著性水平95%的F检验.

3) 拟合优度和自相关检验

拟合优度是用来检验回归方程对样本观测值的拟合程度的，它的值越大说明随机误差所占的比重越小，也就是说回归的效果越显著.拟合优度又可以叫做可决系数，描述的是被解释变量和解释变量之间的线性相关程度.r与r2的值越靠近1，就说明回归方程对样本观测值拟合得越好，表5为所建模型的拟合优度数值.

表5 拟合度检验及DW检验

由表5可知，当r2>0.8时可以说模型拟合的很好，当0.5

Durbin-Waston检验(以下简称DW检验)是推断小样本序列存在自相关的统计检验方法，在这种方法中对DW观测值的直观判断标准为：当DW=2时，残差序列无自相关，DW值越靠近2，残差序列的相关性就越靠近0.要是残差序列自相关，那就说明回归方程并不能够准确地说明被解释变量的变化，即认为方程中忽略了一些影响力比较重大的解释变量.

本文建立的滑出时间解释模型回归方程的DW=1.561，因为DW值较为接近2，所以可以判断回归模型不存在自相关性，残差是独立的，则说明回归方程可靠.

所以，最终滑出时间拟合模型为本文提出的多元线性回归模型能较准确的解释滑出时间影响关系，整体准确率达85%，表明本文提出的影响因素能较好的解释滑出时间的变化，模型见表6.

表6 滑出时间解释模型系数值

由表6可知，航空器离场滑行过程中受其他离场航空器影响最大，特别是滑行过程起飞的航空器对离场滑出时间影响尤为明显，平均每1架离场航空器增加2.6 min，这主要是由于离场队列的长度决定了航空器等待时间，从而使滑出时间明显加长；进场航空器对离场航空器影响较小，主要是由于H机场以隔离运行模式为主，进离场航空器路线分离，仅在场面滑行过程中可能存在冲突，由解释模型可以看出，这种冲突存在次数很少；从运行时段来看，T2(14:00-20:59)时间段内，航空器滑出时间最长，比T1时间段增加了3 min，比T3时间段增加6 min，结合航班延误率可知此T2时间段航班延误传播范围扩大，延误航班不断堆积，场面拥堵情况最为严重，从而导致航空器滑出时间增加.

4 结 束 语

通过对H机场2015年7—9月份航班历史运行数据的分析，采用相关性分析筛选出与滑出时间相关的主要影响因素，应用多重线性回归模型构建了滑出时间模型，并证实了模型的有效性.通过对模型的结果进行分析，可以发现：进离场航空器数量、运行时间段与离场滑行时间有着显著的相关性，并且随着进离港航空器的增加，它们之间的相互作用更加明显.因此，需要综合考虑进场航班对离场航班和离场航班之间的相互影响，实现减少离场航班队列长度，缩减航空器滑出时间.

机场应合理安排航班时刻，避免同一时间段内进离场航空器过多，影响离场效率，在制定缩减滑出时间的策略时应当考虑进场航班对离场航班的影响；同时离场航空器之间的相互影响明显，应当实时调控场面推出航空器数量，减少离场队列长度，缩减航空器滑出时间，从而减少因航空器等待时间过长带来的油量损耗.

[1] IDRIS H, ANAGNOSTAKIS I, DELCAIRE B, et al. Observations of departure processes at logan airport to support the development of departure planning tools[J]. Air Traffic Control Quarterly Journal,1999,7(4):57-60.

[2] REGINA R,CLEWLOW, IOANNIS S, et al. Impact of arrivals on departure taxi operations at airports[C]. Navigation, and Control Conference, Toronto,2010.

[3] BALAKRISHNA P, GANESAN R, SHERRY L, et al. Estimating taxi-out times with a reinforcement learning algorithm[C].Digital Avionics Systems Conference,2008.

[4] BALAKRISHNA P, GANESAN R, SHERRY L. Accuracy of reinforcement learning algorithms for predicting aircraft taxi-out times: a case-study of Tampa Bay departures[J]. Transportation Research Part C Emerging Technologies,2010,18(6):950-962.

[5] JORDAN R, ISHUTKINA M, REYNOLDS T. A statistical learning approach to the modeling of aircraft taxi time[C]. Proceedings of the IEEE/AIAA 29th Digital Avionics Systems Conference (DASC),2010.

[6] RAVIZZA S, ATKIN J A D, MAATHUIS M H, et al. A statistical approach for improving taxi time estimations at airports[J]. Journal of the Operational Research Society,2013,64:1347-1360.

[7] 冯霞,孟金双.基于排队论的航班滑出时间预测[J].南京航空航天大学学报,2017(1):1-10.

[8] 李楠,赵擎,徐肖豪.基于A*算法的机场滑行路径优化研究[J].计算机仿真,2012,29(7)：88-92.

[9] 王翀,汤新民,安宏锋.A-SMGCS航空器动态最优滑行路径规划研究[J].武汉理工大学学报(交通科学与工程版),2012,36(5):1069-1073.

[10] 王媛,胡明华,徐冬慧.机场场面运行延误特性研究[J].武汉理工大学学报(交通科学与工程版),2017,41(3):448-453,457.

[11] 陈功平,王红.改进Pearson相关系数的个性化推荐算法[J].山东农业大学学报(自然科学版),2016(6):940-944.

[12] 栾丽华.聚类算法研究[D].南京：南京师范大学,2004.

[13] 黄文珂.多元回归建模过程中共线性的诊断与解决方法[D].哈尔滨：哈尔滨工业大学,2012.