高原环境连续下坡路段大货车行车速度预测模型*
2018-05-02陈立辉郭忠印
陈立辉 郭忠印
(同济大学道路与交通工程教育部重点实验室 上海 201804)
0 引 言
公路连续下坡路段是事故高发路段[1].与低海拔环境不同,针对高原环境下的连续下坡路段道路安全研究成果较少.高原环境具有典型而恶劣的气候条件,大气压和含氧量随海拔高度升高而降低,海拔高度5 000 m,大气压力下降约46%,大气含氧量下降约46.7%,大气压力和含氧量的降低对交通安全系统会产生一系列影响,首先是对驾驶员的生心理的影响,主要包括反应时间、心率、运动系统等[2-4].其次是对车辆的影响,主要体现在车辆的动力性能和气压制动性能[5-6]上.车辆的实际行驶速度总是随公路线形、车辆性能,以及驾驶员特性等各种条件的改变而改变,高原环境对车辆和驾驶员的影响最终都会通过车辆速度的形式表现出来.
为了研究高原环境连续下坡路段的车速特征,本文以214国道海拔高度4 600~4 800 m的巴颜喀拉山段连续下坡为研究对象,通过VBOX III设备采集试验车辆的连续行车速度数据,分析纵坡参数对行车速度的影响,通过回归分析,建立高原环境连续下坡路段的载重货车行车速度预测模型.
1 试验设计
从试验的角度来看,与使用雷达设备或位于固定点的其他传感器的定点测量不同,本研究采用GPS设备沿车辆行驶路径连续收集速度数据,避免了断面法定点采样的离散型对车速行驶轨迹的破坏.以标准载重49 t的东风天龙半挂车为试验车型,利用安装在车顶的车载VBOX III设备的全球定位系统(GPS),采集国道214线海拔高度4 600~4 800 m的巴颜喀拉山一段连续下坡行车速度数据.
为了防止不同驾驶习惯对试验造成的干扰,本试验选择一名本地驾驶员驾驶试验车辆,数据采集时间间隔为1 s.试验时段选择08:00—16:00的晴朗天气,车流为自由流,试验共进行了20次.
为了排除明显不合理的数据对试验结果产生影响,本试验在数据选择上进行了降噪处理,选择坡度单一、车速稳定路段车速数据作为分析数据来源,排除因不同坡度及车速离散过大对结果造成的影响.
2 运行速度预测模型
2.1 参数选择
影响载重货车下坡路段的行车速度因素有很多,如坡度、坡长、车辆总重量、车辆进入纵坡的初速度、空气阻力、驾驶员技能等.根据本研究目的,结合文献[7-9],选择坡度、坡长作为自变量.
根据实测数据绘制散点图,首先绘制坡度与速度散点图,见图1.根据散点图的变化趋势,结合多模型评估,选择二次多项式作为拟合模型,拟合方程为
y=2.566 3x2-23.548x+76.835
R2=0.644 5
(1)
由判定系数R2=0.644 5可知,坡度与车辆运行速度二次多项式关系较为显著.

图1 坡度与车速关系图
其次,绘制坡长与速度散点图,见图2.同样根据散点图的变化趋势,结合多模型评估,选择二次多项式作为拟合模型,拟合方程为
y=-0.668 5x2+6.917x+19.167
R2=0.601 7
(2)
由判定系数R2=0.601 7可知,坡长与车辆运行速度二次多项式关系同样较为显著.

图2 坡长与车速关系图
2.2 模型构建
根据上述分析,选择二元二次多项式作为拟合模型,设纵坡坡度变量P为,坡长变量L为,车速V为y,回归模型如下为
句中“朝士善历者”为定语后置句式,“善历”为定语,“朝士”为中心语,“者”为定语后置的标志。翻译时应按现代汉语的表达习惯加以调整,即“精通(擅长)历法的朝中大臣”。
(3)
y=a0+a1x1+a2x2+a3x3+a4x4+a5x5(4)
式中:a0为常数项;ai为变量系数,i=1~5.
根据概率原理,y为随机变量,将方程化为矩阵形式:
(5)
yn×1=xn×pap×1+εn×1
(6)
也可记为
y=X·a+ε
(7)
根据残差平方和:
SSR=ε′ε=(y-Xa)′(y-Xa)
(8)
根据最小二乘法原理,通过对残差平方和进行最小化,就可以得到总体参数的最小二乘估计a.
a=(X′X)-1X′y
(9)
通过经典线性回归进行模型构建,排除虽然个别变量参数显著性检验的拟合方程得到满足,但回归方程参数共线性始终无法消除的问题,以及膨胀因子VIF超过10的上限导致共线性严重,致使模型估计失真或难以估计准确,本文通过岭回归的方式,对多元线性回归模型进行岭回归,避免上述问题的出现.
2.2.1岭回归原理
岭回归(ridge regression)是在平方误差的基础上增加正则项,见式(10)~(11),其中,k为岭参数,范围为0~1.0.
Lossfunction=
(11)
2.2.2K值选取
本文通过方差扩大因子法选择k值,方差扩大因子VIF度量了多重共结性的严重程度,一般当与VIF>10 时,模型就有严重的多重共线性.因此,选择k的经验做法是使所有方差扩大因子VIF≤10,这时所对应的k值的岭估计就会相对稳定.
本研究基于R语言进行岭回归分析,图3为岭参数k与膨胀因子VIF的关系图.当VIF≤10时,即可满足回归方程对膨胀系数的要求.由图3可知,岭参数k约为0.4时,膨胀因子VIF在10以内,因此,本文取岭参数为0.4.

图3 岭参数与膨胀因子关系图
根据选择的岭参数k值,可以确定具体的参数估计值,图4为选择不同的岭参数值时对应的膨胀因子VIF值,图中竖向虚线为k取0.4时,对应的回归方程中的参数值.

图4 参数岭轨迹图
当k取0.4时,模型调整后R2=0.65,意味着自变量对因变量的解释程度较好,可以满足回归分析的需要.同时根据德宾-沃森检验值为1.501<10,不存在显著的自相关问题.见表1.

表1 模型摘要
根据回归结果得到的对应参数值及相关显著性检验,见表2.

表2 回归系数及显著性检验
将得到的参数值带入方程,最后得到的回归方程为
y=30.633 2-1.375 6X1+0.961 6X2+
R2=0.65
(12)
将具体的变量代入方程即可得到速度与坡度、坡长的回归方程。
V=30.633 2-1.375 6P+0.961 6L+
0.335 4PL-0.119 1P2+0.12L2
R2=0.65
(13)
3 应用实例分析
为了检验回归模型的适用性及准确性,对原有路段又进行了四次试验,根据不同的坡度及坡长,从四次试验中选择15段纵坡,统计每段纵坡的坡度、坡长和采集到的速度值,将坡度、坡长数据带入得到的行车速度预测模型回,通过实测数据与预测数据对比,验证回归模型的有效性,具体对比见图5.
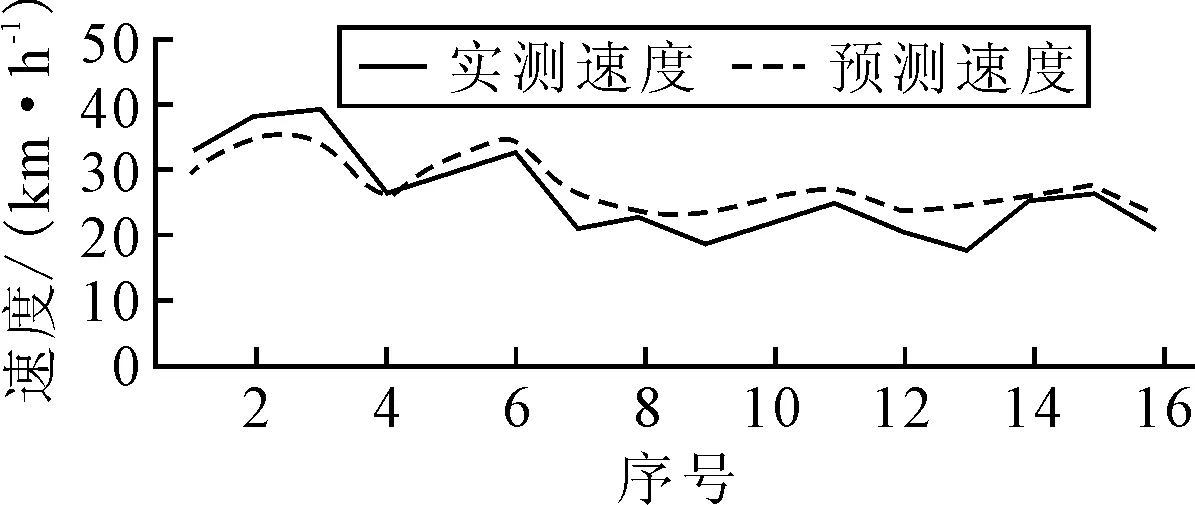
图5 预测车速与实测车速比较图
由图5可知,预测值基本能够反映实测值的趋势,根据数据统计,回归模型平均误差约为7.45%,在可以接受范围.
4 结 束 语
断面法基于断面上大量车辆行车速度的统计学分析,因受断面数量的限制,很难精确描述车辆的实时速度状态特征,基于GPS的连续观测法,可以采集车辆行驶方向上连续的行车速度数据,更加精确的描述行车速度与纵断面参数之间的弥补断面法纵向行车速度的缺点,只要数据量够大,则可以兼顾断面法优点的同时,精确统计纵坡路段上车辆的准确状态特征.
从多变量回归的变量选择来说,普通的多元线性回归要做的是变量的剔除和筛选,而岭回归是一种收缩的方法,而不是删除该变量.岭回归是对最小二乘回归的一种补充,它损失了无偏性,来换取高的数值稳定性,从而得到较高的计算精度,针对共线性问题,是个比较好的方法.
高原环境连续下坡路段的行车速度研究成果较少,本文通过实车试验,大样本量行车速度数据回归海拔4 600~4 800 m的连续下坡路段运行速度预测模型,为高原环境连续下坡路段的设计和安全研究提供了理论基础.本文因试验条件所限,无法兼顾不同载重条件下的车辆试验,需要在进一步的研究中给出修正.
[1] AASHTO A. Policy on geometric design of highways and streets[J]. American Association of State Highway and Transportation Officials, Washington D C,2001(1):158-163.
[2] 叶庆华,陈林声,胡鸿勤.驾驶员进入高原不同海拔高度的反应时改变[J].交通医学,1993(1):14-15.
[3] 艾力·斯木吐拉,李岩岩,伊力扎提·艾力.高原公路驾驶员生理特性动态试验分析[J].中国安全科学学报,2016,26(5):7-12.
[4] 杨国愉,冯正直,汪涛.高原缺氧对心理功能的影响及防护[J].中华行为医学与脑科学杂志,2003,12(4):471-473.
[5] 张永虎,熊云,刘晓,等.富氧进气改善高原汽车发动机动力性和经济性研究[J].汽车技术,2011(3):24-27.
[6] 魏伟,王培强.高原低气压环境下列车制动能力预测[J].铁道车辆,2005,43(12):8-12.
[7] 邓云潮.公路连续下坡路段小客车运行速度预测模型[J].长安大学学报(自然科学版),2009(4):43-47.
[8] 许金良,叶亚丽,苏英平,等.双车道二级公路纵坡段车辆运行速度预测模型[J].中国公路学报,2008(6):31-36.
[9] SAGARDOY R C, GALLEGO M. New approach to defining continuous speed profile models for two-lane rural roads[J]. Transportation Research Record Journal of the Transportation Research Board,2012,23(1):157-167.
