Relationship Between Integer Order Systems and Fractional Order Systems and Its Two Applications

Xuefeng Zhang

I.INTRODUCTION

THE concept of fractional differentiation appeared first in a famous correspondence between L.Hopital and Leibniz,in 1695.Fractional calculus has had a 300 years old history,the development of fractional calculus theory is a matter of almost exclusive interest for few mathematicians and theoretical physicists.In recent years,researchers have noticed that the description of some phenomena is more accurate when the fractional derivative is introduced.Many practical control system models can be described by fractional differential equations.It is worth mentioning that many physical phenomena having memory and genetic characteristics can be described by modeling as fractional order systems.Fractional order systems have attracted much attention.In what concerns automatic control,Hartley and Lorenzo[1]studied the fractional order algorithms for the control of dynamic systems.Podlubny[2]proposed a generalization of the PID controller,namely the PIλDµcontroller,involving an integrator of orderλand a differentiator of orderµ.Liet al.[3]propose the definition of Mittag-Leffler stability and introduce the fractional Lyapunov direct method.Fractional comparison principle is introduced and the application of Riemann-Liouville fractional order systems is extended by using Caputo fractional order systems.Li and Zhang[4]give a survey on the stability of fractional differential equations based on analytical methods.

Fractional-order differential operators present unique and intriguing peculiarities,not supported by their integer-order counterpart,which raise exciting challenges and opportunities related to the development of control and estimation methodologies involving fractional order dynamics.In recent years,most of papers are devoted to the solvability of the linear fractional equation in terms of a special function and to problems of analyticity in the complex domain.Fractional system and its control has become one of the most popular topics in control theory[5]-[8].The number of applications where fractional calculus has been used rapidly grows.These mathematical phenomena allow to describe a real object more accurately than the classical“integer-order”methods[9]-[12].Reference[10]gives the non existence of periodic solutions in fractional order systems with Mellin transform.But for singular fractional order systems,the Mellin transform method is invalid because of singularity of systems.

In this paper,we will show that rational fractional order linear time invariant autonomous system is equivalent to an integer order linear time invariant non-autonomous system but cannot be equivalent to any integer order linear time invariant autonomous system with any system parameters.The nonexistence of periodic solutions of fractional order dynamic systems are proved by means of contradiction method.Stability of a fractional order linear time invariant autonomous system is equivalent to the stability of another corresponding integer order linear time invariant autonomous system.The examples and state figures are given to illustrate the effects of the conclusions derived.The conclusions provided in the paper can be easily extended to singular fractional order linear time invariant systems.

II.PRELIMINARIES

Let us denote by Z+the set of positive integer numbers,C the set of complex numbers,Rn×nthe set ofn×ndimension real numbers.We denote the real part of complex numberαby Re(α).

Caputo derivative has been often used in fractional order systems since it has the practical initial states like that of integer order systems.

Definition 1:The Caputo fractional order derivative with orderαof functionx(t)is de fined as

wheren-1＜α＜n∈Z+,Γ is well-known Euler Gamma function.

Definition 2:The Riemann-Liouville derivative of fractional orderαof functionx(t)is de fined as

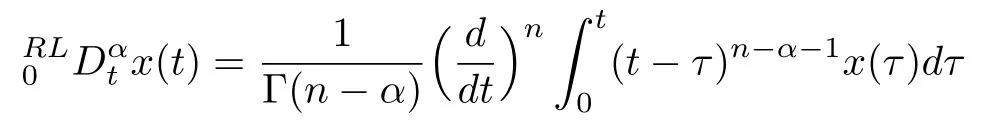
wheren-1＜α＜n∈Z+.

Definition 3:The Grunwald-Letnikov derivative of fractional orderαof functionx(t)is defined as

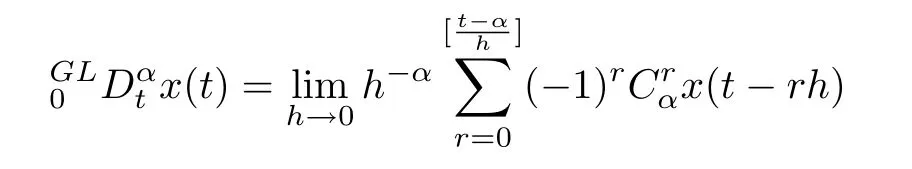
wheren-1＜α＜n∈Z+.

Definition 4:The Mittag-Leffler function is defined as

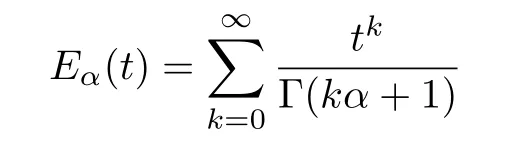
where Re(α)＞0,t∈C.The two-parameter Mittag-Leffler function is de fined as

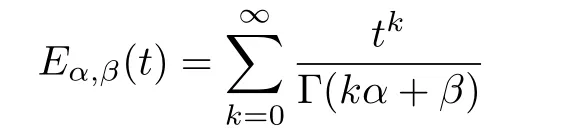
where Re(α)＞0,β,t∈C.

Property 1:The Laplace transform of Caputo derivative of functionx(t)is

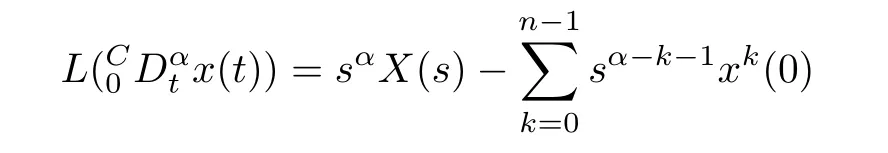
whereX(s)=L[x](s),n-1＜α＜n∈Z+.

Property 2:If letα∈(0,∞)N.Then,we have

wheren-1＜α＜n∈Z+.

Lemma 1:The Laplace transform oftα-1

+/Γ(α)is:

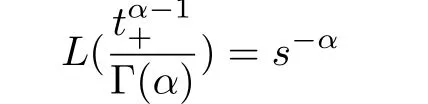
and

Lemma 2:The Laplace transform ofis:

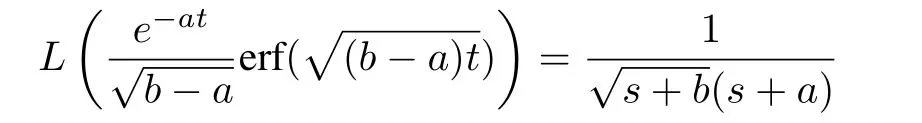
where erf(t)is the error function for each element oft,

Lemma3:The Laplace transform ofis:

where daw(t)is Dawson function for each element oft,

Lemma 4:The Laplace transform ofAcos(ωt)is:

Lemma 5:The Laplace transform oftβ-1Eα,β(-ωtα)is:

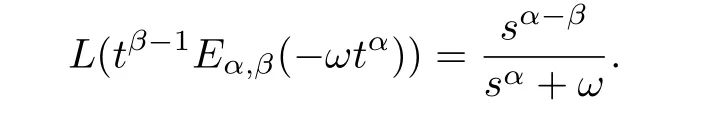
Lemma 6:The Laplace transform ofnorder derivativefn(t)is:

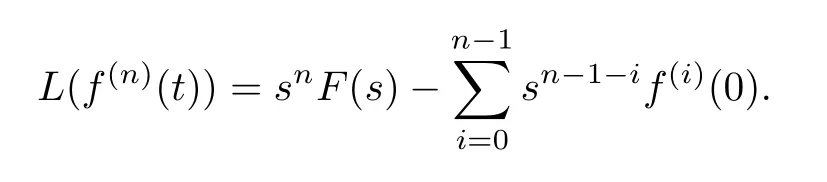
III.MAIN RESULTS

A.Equivalence Between FOS and IOS

Integer order linear time invariant(LTI)systems have been developed quite maturely.Fractional order LTI system is a subsystem of dynamic control system and is less discussed due to its difficulty.In order to obtain the better control cost index,the control components and devices with fractional order properties are needed to be introduced.Algorithms in measurement technology sometimes process the fractional order characteristics.Some control plants are more difficult to be modeled than integer order systems.By the above reason,fractional order dynamic control systems are essential to be introduced.From Fig.1,we can see that state figures of˙x(t)=tx(t),and those ofDαx(t)=x(t),α=0.2,0.4,...,1,are similar to each other,but they are not identically coincided with each other.An obvious question is whether there exists an integer order LTI system(1)equivalent to a fractional order LTI system(2)with any appropriate parameters or be equivalent to a fractional order linear time varying(LTV)system(3)with any appropriate parameters or not.It is an important problem for the reason that if the answer is “yes”so the fractional order systems can be regarded as a part of integer order systems and if the answer is“no”so the fractional order systems cannot be ignored so that the research of fractional order systems(FOS)is magnificently innovative.From the theorems in this section,it is found that the answer is negative.It can hold only if the state is zero solution.Actually,(1)is equivalent to(4)in some cases.In the following subsection,we can have that ifα=1/2,(4)reduces to(5).

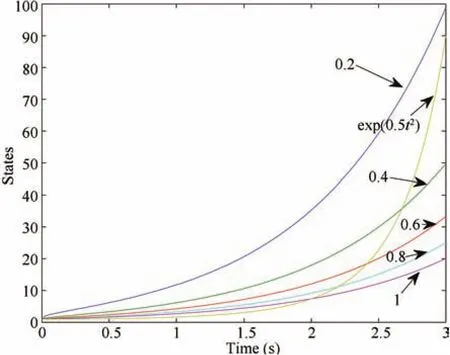
Fig.1.Plot of states of˙x(t)=tx(t)and Dαx(t)=x(t).

From the discussion on relationship between FOS and integer order systems(IOS)in the above subsection,it is easy to introduce its two applications i.e.,non existence of periodic solutions for FOS and stability between FOS and IOS.

B.Non Existence of Periodic Solutions for FOS

Theorem 1:Whileα=1/2,(1)is equivalent to(5).

Proof:Using Laplace transform for(1),taking into account the Caputos definition for the fractional-order derivatives in(2),and applying Property 1 in the case that 0＜α＜1,it yields that

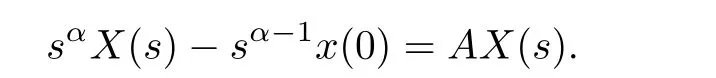
Pre-and post-multiplying above equation bys1-α,it follows that

By Lemma 1 and taking inverse Laplace transform in above equation,we have(4).

Whenα= 1/2,we have(5).If we denoteB=then(5)changes as(6)

Whenα=p/q,p,q∈Z+,(1)can be proved to be equivalent to(7).

whereδis the unit pulse function.

Theorem 2:Whileα=p/q,System(1)is equivalent to(7).

Proof:Using Laplace transform in(1),taking into account the Caputos definition for the fractional-order derivatives in(2),and applying Property 1 in the case that 0＜α＜1,we have that

Pre-and post-multiplying above equation bysp/q,it follows that

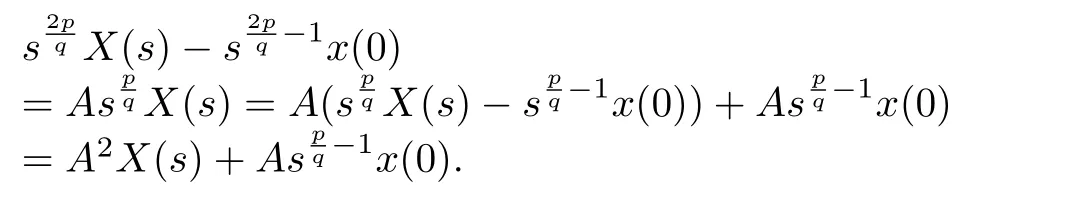
Keeping on pre-and post-multiplying above equation bysp/qtillqtimes,it follows that

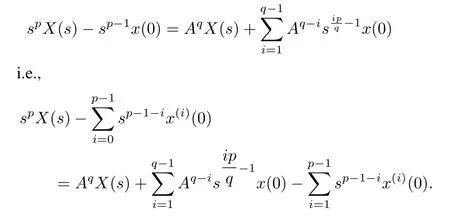
By Lemma 1 and Property 1 and taking inverse Laplace transform in above equation,we have(7).

Theorem 3:Linear time invariant fractional system(1)with order 0＜α＜1,α=p/q,p,q∈Z+has no periodic solution.

Proof:By contradiction,suppose linear time invariant fractional system(1)has a periodic solutionx(t).ForT-periodic functionx(t+T)=x(t),from

it is easy to see thatx(k)(t+T)=x(k)(t).From Theorem 2,we know that(1)is equivalent to(7).If we denote

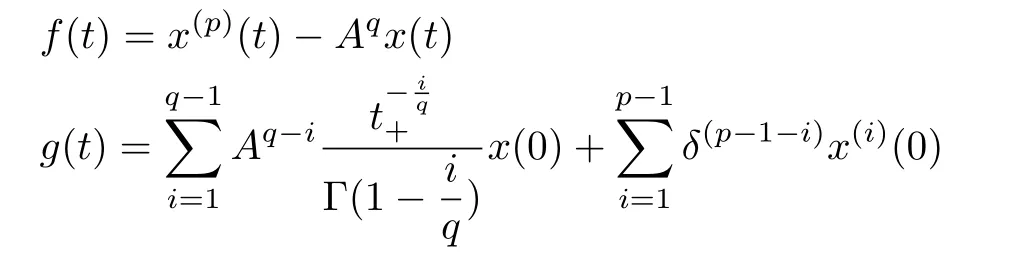
thenf(t)=g(t).However,f(t)is periodic function butg(t)is a non-periodic function.So,there does not exist any periodic solution for(1). ¥

Remark 1:From Theorem 2,we know that there does not exist any integer order LTI system(2)be equivalent to a fractional order LTI system(7)with any appropriate parameters.It means the properties of fractional order LTI systems may be different from those of integer order LTI systems.It can attract researchers to explore the distinct properties of fractional order LTI systems.

Remark 2:Theorem 3 gives a concise and effective proof that there does not exist periodic solutions for fractional order LTI(7).

Remark 3:With the equivalence between the integer order LTI(7)and the fractional order LTI(1),we succeed in finding a new research approach of discussing the difficult fractional order LTI(1).However,relative to(1),it is easy and there exists extensive results to discuss the integer order LTI(7).For example,we can further discuss the stability and robust stability of fractional order LTI system(1)in the future.

Remark4:From Theorem 3,we can see that only ifαis an integer,it followsg(t)=0.This means only ifαis an integer,it is possible for(1)to satisfy periodic solutions.

C.Stabilities Between FOS and IOS

Lemma 7[12]:System(1)with 0＜α＜1 is asymptotically stable if and only if there exist two matricesX,Y∈Rn×n,such that

wherea=sin(απ/2),b=cos(απ/2).

Lemma 8[12]:System(1)with 1＜α＜2 is asymptotically stable if and only if there exist two matricesX,Y∈Rn×n,such that

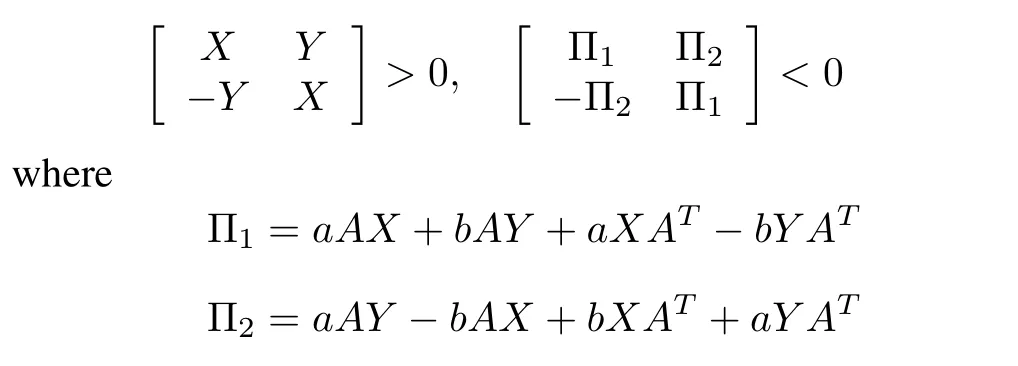
anda,bare the same as those in Lemma 7.

Lemma 9[12]:A complex matrixX∈Cn×nsatis fiesX＜0 if and only if

Consider the following specific complex integer order linear time invariant system:

where system matrixA∈Rn×n,jis the imaginary unit.

Using Lyapunov theory of integer order systems and Lemmas 7 and 8,it is easy to obtain the following equivalence stability criterion.

Theorem 4:Fractional order system(1)with 1＜α＜2 is asymptotically stable if and only if integer order system(9)is asymptotically stable.

Proof:For the specific complex integer order LTI system(9),we choose the quadratic Lyapunov candidate function as

whereX+jY＞0.Then,differentiatingV(x(t))with respect to timetalong to the solution of(9),we obtain

Using Lyapunov theory of complex integer order systems and considering(8)in Lemma 9,this completes the proof.

IV.NUMERICAL EXAMPLES

Example1:Consider integer order system(2)with parameters as follows:

from Fig.2,we can see that the solutions are periodic.But if we consider(1)with the same above parameters andα=1/2,then by Laplace transform for(1)we have

Fig.2. State curves of IOS in Example 1.

It is easy to obtain the solutions of the above equations as follows:

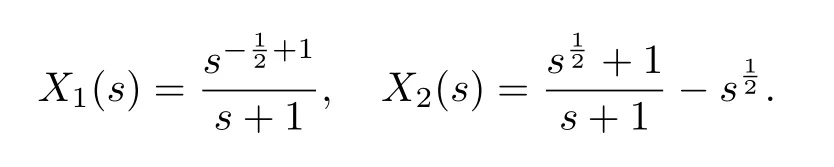
Consider Lemmas 1 and 3,and take the inverse Laplace transform forX1(s)andX2(s),it follows that:

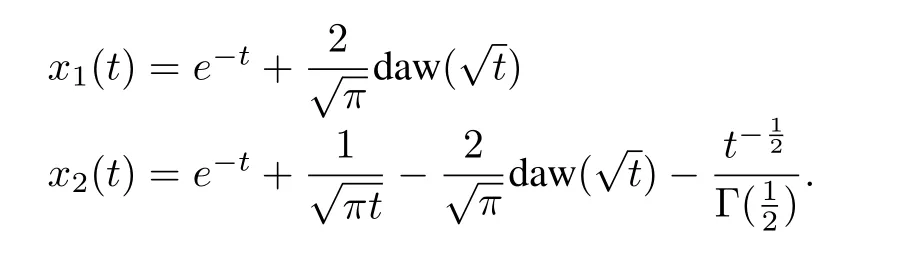
With Lemma 5,it also follows that:

It is easy to see from Fig.3 that the state curves of fractional order system(1)with parameterα=1/2 do not possess periodic dynamic orbits.

Fig.3.State curves of FOS in Example 1.

Example2:By Theorem 2,forα=1/3,we have that(1)is equivalent to

From Fig.4,we can see the state curves of fractional order system(1)with parameterα=1/3 are completely identical to the corresponding state curves of integer order(7).

Fig.4. State curves of FOS in Example 2.

V.CONCLUSIONS

Many systems exhibit the fractional phenomena,such as motions in complex media or environments,random walk of bacteria in fractal substance,etc.These models can be obtained by solving modified fractional order systems.In this paper,we discuss the relationship between rational fractional order systems and integer order systems and conclude that the two kind of systems cannot be substituted for each other.The criteria of nonexistence of periodic solution of fractional order systems are addressed.The proof approach is based on the properties of Laplace transform of fractional order systems.Stability of a fractional order linear time invariant autonomous system is equivalent to the stability of another corresponding integer order linear time invariant autonomous system.Some numerical examples are given to verify the feasibility of results presented.The methods provided in the paper can be extended to singular fractional order linear time invariant systems in the future.

[1]T.T.Hartley and C.F.Lorenzo,“Dynamics and control of initialized fractional-order systems,”Nonlinear Dyn.,vol.29,no.1-4,pp.201-233,Jul.2002.

[2]I.Podlubny, “Fractional-order systems and PIλDµ-controllers,”IEEE Trans.Auto.Control,vol.44,no.1,pp.208-214,Jan.1999.

[3]Y.Li,Y.Q.Chen,and I.Podlubny,“Mittag-Leffler stability of fractional order nonlinear dynamic systems,”Automatica,vol.45,no.8,pp.1965-1969,Aug.2009.

[4]C.P.Li and F.R.Zhang,“A survey on the stability of fractional differential equations,”Eur.Phys.J.Special Topics,vol.193,no.1,pp.27-47,Mar.2011.

[5]Z.Liao,C.Peng,W.Li,and Y.Wang,“Robust stability analysis for a class of fractional order systems with uncertain parameters,”J.Franklin Inst.,vol.348,no.6,pp.1101-1113,Aug.2011.

[6]C.P.Li and W.H.Deng, “Remarks on fractional derivatives,”Appl.Math.Comput.,vol.187,no.2,pp.777-784,Apr.2007.

[7]H.J.Haubold,A.M.Mathai,and R.K.Saxena,“Mittag-Leffler functions and their applications,”J.Appl.Math.,vol.2011,Article ID 298628,Feb.2011.

[8]A.Erd´elyi,Tables of Integral Transforms.New York:McGraw-Hill,1954.

[9]J.Sabatier,M.Moze,and C.Farges,“LMI stability conditions for fractional order systems,”Comput.Math.Appl.,vol.59,no.5,pp.1594-1609,Mar.2010.

[10]E.Kaslik and S.Sivasundaram,“Non-existence of periodic solutions in fractional-order dynamical systems and a remarkable difference between integer and fractional-order derivatives of periodic functions,”Nonlinear Anal.:Real World Appl.,vol.12,no.3,pp.1489-1497,Jun.2012.

[11]R.L.Bagley and R.A.Calico,“Fractional order state equations for the control of viscoelastically damped structures,”J.Guidance Control Dyn.,vol.14,no.2,pp.304-311,Mar.1991.

[12]X.F.Zhang and Y.Q.Chen,“D-stability based LMI criteria of stability and stabilization for fractional order systems,”inProc.ASME 2015 Int.Design Engineering Technical Conf.&Computers and Information in Engineering Conf.,Boston,USA,2015.