Relief Materials Vehicles Planning in Natural Disasters

Qun Shi,Wen Yang,Zhen-Ming Yang,and Qian-Chuan Zhao,

I.INTRODUCTION

THE The field of emergency relief has been developing rapidly in recent years.The concept of emergency logistics is proposed firstly in[1].Governments evaluate the requirement of the victims at once after natural disasters[2].At the same time,governments build relief materials repositories and parking lots.Usually,the storage capacity of the repositories is limited[3].Also,the vehicles have to leave the parking lots as soon as possible after unloading the relief materials for the reason that the parking spaces are limited.The vehicle routing and scheduling problems with time window constraints are widely studied[4]-[7],because all kinds of relief materials must be transported for the victims within a certain period of time[8]-[10].

Different kinds of natural disasters have their respective evolution characteristics[11]-[13].The changes of the disaster situation are embodied in the kinds and amounts of relief materials[14]-[16].The changes of the vehicles include the source and quantity of ordinary vehicles[17]-[19].Relief materials vehicles planning is dynamic because of the two factors mentioned above[20]-[23].The demand from the victims for relief materials is uncertain,and for such occasion,stochastic programming can be applied to plan relief materials vehicles[24].

Relief materials vehicles planning is a kind of complex optimization problem with the characteristics as follows.There are multiple optimization goals[25]-[28]and many constraint conditions[29]-[31].The optimization goals and constraint conditions are dynamic.The time complexity and space complexity of the algorithms are usually high,as a result,the near optimum solution can be obtained but not the optimum solution.The complexity of problems about relief materials vehicles planning and the results on the worst-case performance of approximation algorithms are studied in[32].For the problems about relief materials vehicles planning,many mathematical models are summarized by the researchers[33],[34].The solution methods mainly include integer programming[35],ant colony algorithm[36],genetic algorithm[37],adaptive large neighborhood search heuristic[38],memetic algorithm[39].

The remainder of the paper is organized as follows.Section II gives the definitions of ordinary vehicles,maneuverable vehicles and transportation fleet.Then,the formal description of the problem with relief materials vehicles planning is presented considering the substitution among the vehicles.Section III proposes a new method called Substitution Equilibrium Point.And the comparison between the new method and integer programming is studied.Section IV conducts four simulation experiments and analyzes the results.At last,Section V concludes this paper.

II.PROBLEM FORMULATION

Many kinds of relief materials in proportion to the victims need has to be transported to the disaster hit areas after natural disasters.This paper presents a problem about planning relief materials vehicles.The numbers of the vehicles from governments and armies can be calculated after the numbers of the vehicles from hospitals,enter prises,social organizations,individuals according to a certain proportion for maximizing the total weight of relief materials.For ease of description,some basic definitions are listed as follows.

Definition 1:The vehicles which can only transport certain kind of relief materials are defined as ordinary vehicles,denoted byXi,i=1,...,n.

The load capacity of each kind of ordinary vehiclesXi,is denoted bym0i,i=1,...,n.

The example of ordinary vehicles can be found as the vehicles from hospitals,enter prises,social organizations and individuals.

Definition 2:The vehicles which can transport all kinds of relief materials are defined as maneuverable vehicles,for example,the vehicles from governments and armies.This paper supposes that there is only one kind of maneuverable vehicle,denoted byY.The load capacity of this kind of maneuverable vehicleYis denoted bym0.

Definition 3:The numbers of all kinds of ordinary vehicles are in certain proportion because the numbers of all the relief materials for the victims are in proportion.

All kinds of ordinary vehiclesXi,i=1,...,n,whose numbers are denoted byx0i,constitute a transportation fleet.

The total load capacity of all the ordinary vehicles in a transportation fleet is defined as fleet load capacity,denoted bym.

Definition 4:The substitution between the maneuverable vehicle and ordinary vehicles is de fined as follows.When some kinds of ordinary vehiclesXi,i∈{1,...,n}are not enough,Ycan substitute forXiin certain proportionsi.

YandXi,i=1,...,nconstitute a transportation fleet while the fleet load remains the same.Different kinds of ordinary vehicles cannot substitute for each other.

Definition 5:Substitute the maneuverable vehicles for the ordinary vehicles till the numbers of the fleets that all kinds of ordinary vehicles constitute are equal.In this case,the numbers of the maneuverable vehicles which substitute for all kinds of ordinary vehicles are defined as substitution equilibrium point.

Now we build the mathematical model for the problem about planning relief materials vehicles.The decision variables of the problem are divided into four parts as follows:

1)number of the transportation fleetsf;

2)numbers of all kinds of ordinary vehiclesxi,i=1,...,n;

3)number of the maneuverable vehiclesy;

4)substitution equilibrium pointyi,i=1,...,n,wheref,xi,y,yi∈Z.

The objective of the problem is formulated as

The constraints are as follows.

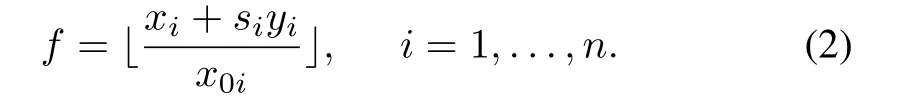
In(2),Xiwhose number issiyihas the same load asYwhose number isyi,m0isiyi=m0yi,si=m0/m0i.

Substitution equilibrium pointyisatis fies

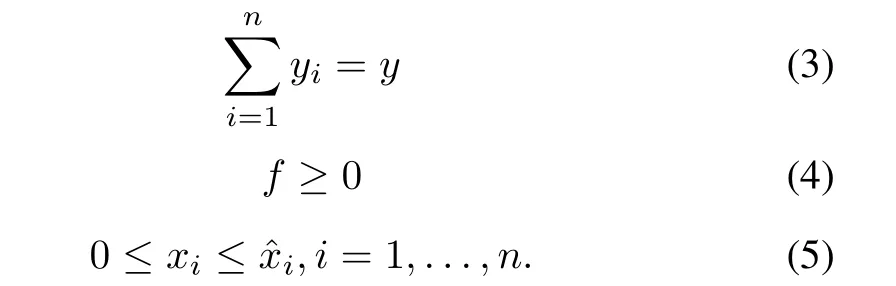
In(5),ˆxiis the upper bound ofxi.

In(6),ˆyis the upper bound ofy.

The numbers of the vehicles from hospitals,enterprises,social organizations,individuals are uncertain after natural disasters.We suppose the ranges ofare known,Also,the numbers of the vehicles from governments and armies are uncertain.We suppose the range ofis known,

Apparently,the greater the numbers of ordinary and maneuverable vehicles,the greater will be the numbers of transportation fleets and total weight of relief materials.The solution results are called conservative decisions,when1,...,nin(5)andin(6).Conversely,the solution results are called optimistic decisions,when1,...,nin(5)and=in(6).

III.SOLUTION METHODOLOGY

Now we present two kinds of solution methods for the mathematical model of the problem about planning relief materials vehicles built in Section II.

The first solution method is called substitution equilibrium point.

Expanding(2),we have

Transform(8)and(3)into matrix form

where

The matrixAin(10)is an invertible matrix,in other words,A-1certainly exists.

Proof:

The greaterxi,i=1,...,nandyare,the greater isf.The 1st generation substitution equilibrium point for all kinds of ordinary vehicles can be solved according to(9)whenxi=,i=1,...,nandy=

When there is only one positive element inwhose subscript is denoted byk,the ordinary vehicleXkneeds to be substituted,soyk=y.In this case,the number of the transportation fleets is

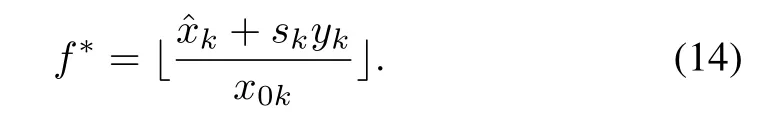
And the total number of all kinds of ordinary vehicles is

When there are negative elements inand the number of the positive elements inis more than one,the subscripts of the negative elements inconstitute the setandAccordingly,the subscripts of the nonnegative elements inconstitute the setare in excess,sodo not need to be substituted byY.Conversely,are not enough,soneed to be substituted byY.

The 2nd generation substitution equilibrium point forcan be solved according to(10),(12),(13),denoted byWhen there are negative elements inthe subscripts of the negative elements inconstitute the setandAccordingly,the subscripts of the nonnegative elements inconstitute the setandare in excess,sodo not need to be substituted byY.Conversely,are not enough,soneed to be substituted byY.

According to(3),

According to(17),

The next generation of substitution equilibrium point forcan be solved according to the above steps under two different cases as follows.

Case 1:Solve substitution equilibrium point generation after generation till all the elements inare nonnegative,The ordinary vehiclesneed to be substituted byY,and the others inXi,i=1,...,ndenoted bydo not need to be substituted byY.In all the transportation fleets,the numbers ofare.In this case,the number of the transportation fleets is

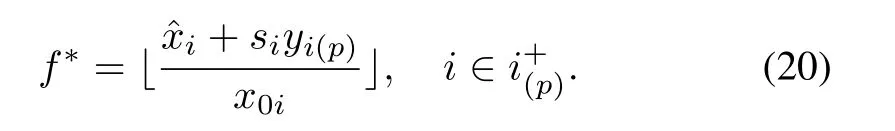
Xi,are in excess,sodo not need to be substituted by

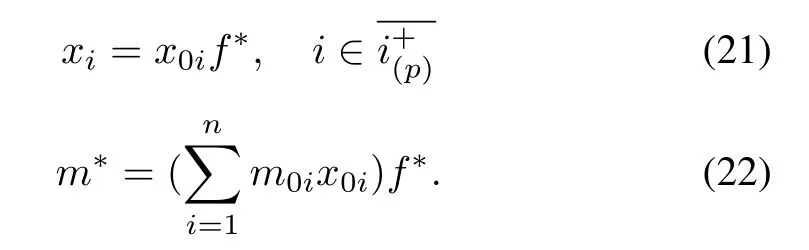
Case 2:Solve substitution equilibrium point generation after generation till there is only one positive element indenoted byyk.The ordinary vehicleXkneeds to be substituted byY,andyk=y.Conversely,the others inXi,i=1,...,ndo not need to be substituted byY.The number of the transportation fleets can be solved according to(14).The numbers of all kinds of ordinary vehicles can be solved according to(15)and(16).

The algorithm used to plan relief materials vehicles on the basis of substitution equilibrium point is given as follows.

Algorithm 1:

本研究主要通过调查问卷的方式进行。调查问卷为英语听力学习策略的调查问卷。调查问卷使用Likert五级量表，选项从1到5分别表示从“这个选项完全或基本上完全不适合我的情况”到“完全或基本完全适合”的五个等级计分。最后，使用社会科学统计软件(SPSS)进行描述性统计。

Step 1:Suppose the ordinary vehicles in the setXneed to be substituted byY.Xis initialized to containXi,i=1,...,n.

Step 2:All the ordinary vehicles inXare denoted byXi(X).ˆxiare substituted into the numbers ofXi(X),and ˆyis substituted into the number ofY.Solve the substitution equilibrium pointy∗ofXaccording to(10),(12),(13).

Step 3:When all the elements iny∗are nonnegative and the number of the positive elements iny∗is more than one,go to Step 4.When there is only one positive element iny∗denoted byyk,go to Step 5.When there are negative elements iny∗and the number of the positive elements iny∗is more than one,the subscripts of the negative elements iny∗constitute the seti-,andyi,i∈i-.Accordingly,the subscripts of the nonnegative elements iny∗constitute the seti+,andyi,i∈i+.Xis composed ofyi,i∈i+,go to Step 2.

Step 4:Solve the decision variables as follows:

1)solve the number of the transportation fleetsfaccording to(20);

2)for all kinds of ordinary vehicles inXdenoted byXi(X),the numbers arexˆi.For the rest inXdenoted byXi(),the numbers can be solved according to(21);

3)the number of the maneuverable vehicles isyˆ;

Step 5:Solve the decision variables as follows:

1)solve the number of the transportation fleetsfaccording to(14);

2)solve the numbers of all kinds of ordinary vehicles according to(15)and(16);

3)the number of the maneuverable vehicles isˆy;

4)the substitution equilibrium point are as follows.

The complexity and convergence of Algorithm 1 are analyzed now.In Step 1,Xis initialized to containXi,i=1,...,n.Each time in Step 3,the kinds of the ordinary vehicles inXare less and less till Step 4 and Step 5,then Algorithm 1 stops.

Xis updated no more thann-2 times in Step 3 of Algorithm 1.Going to Step 2 from Step 3 each time,only one matrix inversion and one matrix multiplication are performed.The primary transform can be used to solve the inverse matrix of the matrixAwhose time complexity isO(n3).Becausenis generally small in practice,Algorithm 1 can satisfy the real time request of planning the relief materials vehicles.

Then,the second solution method for the mathematical model built in Section II is integer programming.

The decision variables of the problem are:

1)f,xi,y,yi∈R;i=1,...,n;

2)the objective of the problem is described by(1);

3)the constraints of the problem are(2)-(7).

Because of the high time complexity,the integer programming method cannot satisfy the real time request of planning the relief materials vehicles.

Now we discuss the vehicles planning problem for uncertain number of vehicles.Supposesolve the model with the method of Substitution Equilibrium Point.Solve the conservative decisions when the number ofXi(X)andYareandin Step 2,respectively.Conversely,solve the optimistic decisions when the number ofXi(X)andYareandin Step 2,respectively.

IV.SIMULATION EXPERIMENTS

Experiment 1:Suppose the maneuverable vehicles do not substitute for the ordinary vehicles,and the numbers ofXiare=1,...,7.Solve the conservative decisions using Algorithm 1 according to substitution equilibrium point.The number of the transportation fleets constituted by the seven kinds of ordinary vehicles is 24.The total weight of the relief materials all the ordinary vehicles can transport is 19176 tons.The numbers of the seven kinds of ordinary vehicles are shown in Table II.

Experiment 2:Suppose the maneuverable vehicles do not substitute for the ordinary vehicles,and the numbers ofXiare=1,...,7.Solve the optimistic decisions using Algorithm 1 according to substitution equilibrium point.The number of the transportation fleets constituted by the seven kinds of ordinary vehicles is 27.The total weight of the relief materials all the ordinary vehicles can transport is 21573tons.The numbers of the seven kinds of ordinary vehicles are shown in Table III.

TABLE IPROPERTIES OF THE VEHICLES

TABLE IICONSERVATIVE DECISIONS WITHOUT MANEUVERABLE VEHICLES

TABLE IIIOPTIMISTIC DECISIONS WITHOUT MANEUVERABLE VEHICLES

Comparison of the conservative decisions in Experiment 1 and optimistic decisions in Experiment 2 is shown in Fig.1.

Experiment 3:The number ofXi,i=1,...,7 andYareandrespectively.Solve the conservative decisions using Algorithm 1 according to substitution equilibrium point and integer programming.The number of the transportation fleets is 43.The total weight of the relief materials all the ordinary vehicles can transport is 34357tons.The numbers of the seven kinds of ordinary vehicles are shown in Table IV.

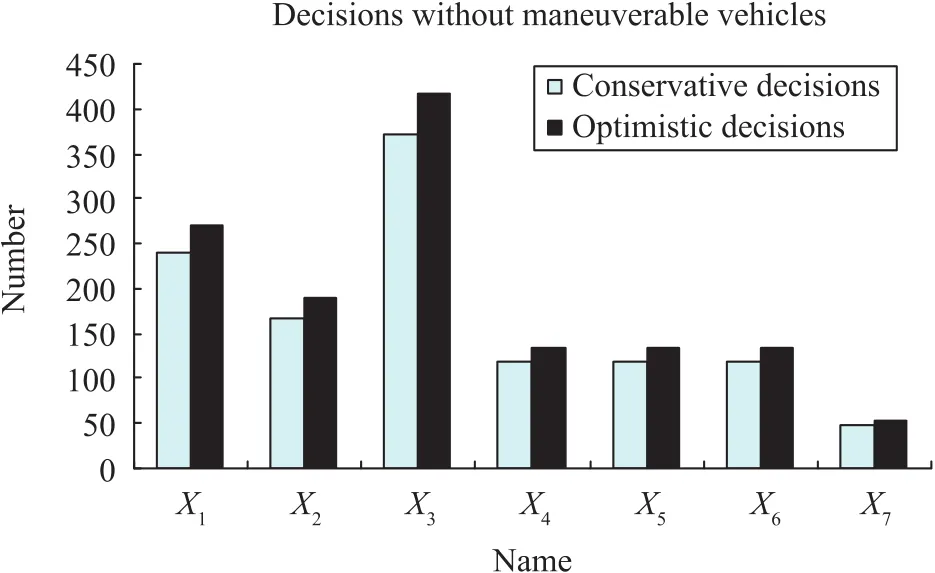
Fig.1. Comparison of the conservative and optimistic decisions without maneuverable vehicles.

TABLE IVCONSERVATIVE DECISIONS AND SUBSTITUTION EQUILIBRIUM POINT

Experiment 4:The number ofXi,i=1,...,7 andYareandrespectively.Solve the optimistic decisions using Algorithm 1 according to substitution equilibrium point and integer programming.The number of the transportation fleets is 54.The total weight of the relief materials all the ordinary vehicles can transport is 43146tons.The numbers of the seven kinds of ordinary vehicles are shown in Table V.

TABLE VOPTIMISTIC DECISIONS AND SUBSTITUTION EQUILIBRIUM POINT

Comparison of the conservative decisions in Experiment 3 and optimistic decisions in Experiment 4 is shown in Fig.2.

Fig.2.Comparison of the conservative and optimistic decisions with maneuverable vehicles.

Comparison of the substitution equilibrium point in Experiment 3 and in Experiment 4 is shown in Fig.3.

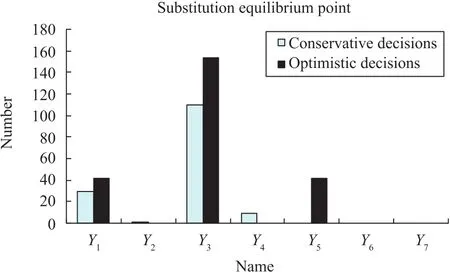
Fig.3. Comparison of the substitution equilibrium point.

Comparison of the CPU time of substitution equilibrium point and integer programming in Experiment 3 and Experiment 4 is shown in Table VI.

The solving environment is as follows:

1)software:MATLAB(2009B,32bit);

2)CPU:Intel(R)Core(TM)i3-3220,3.30GHz;

3)RAM:4.00GB(3.88GB available).

TABLE VICOMPARISON OF THE CPU TIME OF SUBSTITUTION EQUILIBRIUM POINT AND INTEGER PROGRAMMING

Table VI shows that substitution equilibrium point has lower time complexity than integer programming for the problem about planning relief materials vehicles.

In Experiment 4,for example,the substitution equilibrium point is solved three times.

1)Solve the inverse matrix of the matrixA7×7,then solve the substitution equilibrium point ofX1,X2,X3,X4,X5,X6,X7.The results show thatYdo not substitute forX6,X7;

2)Solve the inverse matrix of the matrixA5×5,then solve the substitution equilibrium point ofX1,X2,X3,X4,X5.The results show thatYdo not substitute forX2,X4;

3)Solve the inverse matrix of the matrixA3×3,then solve the substitution equilibrium point ofX1,X3,X5.The results show that onlyX1,X3,X5need to be substituted byY.

V.CONCLUSION

This paper investigates the research results about planning relief materials vehicles.Then,this paper defines the ordinary vehicles and maneuverable vehicles considering the substitution between them.On this basis,this paper presents a problem about planning relief materials vehicles with formal description.The objective of the problem is maximizing the total weight of relief materials and the primary constraints are about the substitution between the ordinary and maneuverable vehicles.This paper proposes a new method called substitution equilibrium point which is compared with integer programming.Finally,the paper carries out four simulation experiments,and the conclusions are as follows.The two methods give the same results,but substitution equilibrium point has much lower time complexity.

Summary of the innovations and characteristics of this paper are as follows.

1)This paper defines the ordinary vehicles and maneuverable vehicles according to the actual conditions of transporting relief materials.Then,this paper defines the substitution between them and gives the quantitative computation method of the transportation fleets.

2)This paper emphasizes on the foremost goal that limited vehicles in proportion can transport the most relief materials.

3)This paper considers that the numbers of all kinds of the vehicles are uncertain.And the uncertain numbers are described by an interval.The results of planning the vehicles are divided into two types which are called the conservative and optimistic decisions.

4)This paper proposes a new method called substitution equilibrium point with polynomial complexity.Compared with integer programming,substitution equilibrium point is more suitable for planning the vehicles in real time.

[1]Z.W.Ou,H.Y.Wang,D.L.Jiang,B.L.Lu,W.X.Gan,and J.Liang,“Emergency logistics,”J.Chongqing Univ.Nat.Sci.Ed.,vol.27,no.3,pp.164-167,2004.

[2]J.B.Sheu,“An emergency logistics distribution approach for quick response to urgent relief demand in disasters,”Transp.Res.Part E Logist.Transp.Rev.,vol.43,no.6,pp.687-709,Nov.2007.

[3]B.L.Davis,F.Samanlioglu,X.L.Qu,and S.Root,“Inventory planning and coordination in disaster relief efforts,”Int.J.Prod.Economic.,vol.141,no.2,pp.561-573,Feb.2013.

[4]M.Huang,K.R.Smilowitz,and B.Balcik,“A continuous approximation approach for assessment routing in disaster relief,”Transp.Res.Part B Methodol.,vol.50,pp.20-41,Apr.2013.

[5]P.Kalina,J.Vok´r´ınek,and V.Ma´r´ık, “Agents toward vehicle routing problem with time windows,”J.Intell.Transp.Syst.Technol.Plann.Operat.,vol.19,no.1,pp.3-17,2015.

[6]R.Spliet and G.Desaulniers,“The discrete time window assignment vehicle routing problem,”Eur.J.Oper.Res.,vol.244,no.2,pp.379-391,Jul.2015.

[7]C.L.Liu and H.C.Shen,“Two-objective optimization model for discrete emergent supply system,”Chin.J.Manage.Sci.,vol.11,no.4,pp.27-31,Aug.2003.

[8]J.B.Sheu and C.Pan,“Relief supply collaboration for emergency logistics responses to large-scale disasters,”Transport.A Transp.Sci.,vol.11,no.3,pp.210-242,2015.

[9]B.L.Liu and T.Ma,“Research on the scheduling problem of emergency materials,”J.Harbin Univ.,no.3,pp.3-5,17,2007.

[10]C.L.Liu,J.M.He,and J.J.Shi,“The study on optimal model for a kind of emergency material dispatch problem,”Chin.J.Manage.Sci.,vol.9,no.3,pp.29-36,Jun.2001.

[11]Y.Homma,T.Watari,T.Baba,M.Suzuki,T.Shimizu,Y.Fujii,Y.

Takazawa,Y.Maruyama,and K.Kaneko,“Injury patterns after the landslide disaster in Oshima,Tokyo,Japan on October 16,2013,”Disaster Med.Public Health Prep.,vol.10,no.2,pp.248-252,2016.

[12]Y.Sun,H.Chi,and C.L.Jia,“Nonlinear mixed-integer programming model for emergency resource dispatching with multi-path,”Oper.Res.Manage.Sci.,vol.16,no.5,pp.5-8,Oct.2007.

[13]G.J.Ji and C.H.Zhu,“Study on the distribution optimal problem in emergency logistics for emergency ecent,”China Busin.Mark.,vol.21,no.3,pp.18-21,2007.

[14]A.Bozorgi-Amiri,M.S.Jabalameli,M.Alinaghian,and M.Heydari,“A modified particle swarm optimization for disaster relief logistics under uncertain environment,”Int.J.Adv.Manuf.Technol.,vol.60,no.1-4,pp.357-371,Apr.2012.

[15]Z.P.Fan,Y.Liu,and R.J.Shen,“Risk decision analysis method for emergency response based on prospect theory,”Syst.Eng.Theory Pract.,vol.32,no.5,pp.977-984,May 2012.

[16]T.Shen,Q.C.Zhao,and D.Z.Zheng, “An inventory control policy,”Acta Autom.Sinica.,vol.25,no.3,pp.337-343,May 1999.

[17]C.Miao,W.S.Xu,and Q.D.Wu,“A transportation modal and solution of large-scale emergency relief commodities,”Syst.Eng.,vol.24,no.11,pp.6-12,Nov.2006.

[18]Y.J.Han,X.H.Guan,and L.Y.Shi,“Optimization based method for supply location selection and routing in large-scale emergency material delivery,”IEEE Trans.Autom.Scinica.Eng.,vol.8,no.4,pp.683-693,Oct.2011.

[19]A.Moreno,D.Alem,and D.Ferreira,“Heuristic approaches for the multiperiod location-transportation problem with reuse of vehicles in emergency logistics,”Comput.Oper.Res.,vol.69,pp.79-96,May 2016.

[20]E.Lalla-Ruiz,C.Expo´sito-Izquierdo,S.Taheripour,and S.Voβ,“An improved formulation for the multi-depot open vehicle routing problem,”OR Spectr.,vol.38,no.1,pp.175-187,Jun.2016.

[21]M.M.L.Nappi and J.C.Souza,“Disaster management:hierarchical structuring criteria for selection and location of temporary shelters,”Nat.Hazard,vol.75,no.3,pp.2421-2436,Feb.2015.

[22]M.Rezaei-Malek,R.Tavakkoli-Moghaddam,B.Zahiri,and A.Bozorgi-Amiri,“An interactive approach for designing a robust disaster relief logistics network with perishable commodities,”Comput.Industr.Eng.,vol.94,pp.201-215,Apr.2016.

[23]B.Saeidian,M.S.Mesgari,and M.Ghodousi,“Evaluation and comparison of genetic algorithm and bees algorithm for location-allocation of earthquake relief centers,”Int.J.Dis.Risk Reduct.,vol.15,pp.94-107,Mar.2016.

[24]M.Ahmadi,A.Sei fi,and B.Tootooni,“A humanitarian logistics model for disaster relief operation considering network failure and standard relief time:a case study on San Francisco district,”Transport.Res.Part E Logist.Transport.Rev.,vol.75,pp.145-163,Jun.2015.

[25]Y.J.Zheng and H.F.Ling,“Emergency transportation planning in disaster relief supply chain management:a cooperative fuzzy optimization approach,”Soft Comput.,vol.17,no.7,pp.1301-1314,Jul.2013.

[26]M.Huang,K.Smilowitz,and B.Balcik,“Models for relief routing:equity,efficiency and efficacy,”Transp.Res.Part E Logist.Transp.Rev.,vol.48,no.1,pp.2-18,Jan.2012.

[27]S.Rath and W.J.Gutjahr,“A math-heuristic for the warehouse locationrouting problem in disaster relief,”Comput.Oper.Res.,vol.42,pp.25-39,Feb.2014.

[28]Y.Pan,J.Yu,and D.L.Da,“Emergency resources scheduling on continuous consumption system based on particle swarm optimization,”J.Syst.Eng.,vol.22,no.5,pp.556-560,Oct.2007.

[29]A.Afshar and A.Haghani,“Modeling integrated supply chain logistics in real-time large-scale disaster relief operations,”Socioecon.Plann.Sci.,vol.46,no.4,pp.327-338,Dec.2012.

[30]T.Vidal,T.G.Crainic,M.Gendreau,and C.Prins,“A unified solution framework for multi-attribute vehicle routing problems,”Eur.J.Oper.Res.,vol.234,no.3,pp.658-673,May 2014.

[31]T.Vidal,T.G.Crainic,M.Gendreau,and C.Prins,“Heuristics for multiattribute vehicle routing problems:a survey and synthesis,”Eur.J.Oper.Res.,vol.231,no.1,pp.1-21,Nov.2013.

[32]J.K.Lenstra and A.H.G.Rinnooy Kan,“Complexity of vehicle routing and scheduling problems,”Networks,vol.11,no.2,pp.221-227,Jun.1981.

[33]L.E.de la Torre,I.S.Dolinskaya,and K.R.Smilowitz,“Disaster relief routing:integrating research and practice,”Socioecon.Plann.Sci.,vol.46,no.1,pp.88-97,Mar.2012.

[34]V.Pillac,M.Gendreau,C.Gue´ret,and A.L.Medaglia,“A review of dynamic vehicle routing problems,”Eur.J.Oper.Res.,vol.225,no.1,pp.1-11,Feb.2013.

[35]D.Gulczynski,B.Golden,and E.Wasil,“The multi-depot split delivery vehicle routing problem:an integer programming-based heuristic,new test problems,and computational results,”Comput.Industr.Eng.,vol.61,no.3,pp.794-804,Jun.2011.

[36]Q.L.Ding,X.P.Hu,L J.Sun,and Y.Z.Wang,“An improved ant

colony optimization and its application to vehicle routing problem with time windows,”Neurocomputing,vol.98,pp.101-107,Dec.2012.

[37]D.Berkoune,J.Renaud,M.Rekik,and A.Ruiz,“Transportation in disaster response operations,”Socioecon.Plann.Sci.,vol.46,no.1,pp.23-32,Mar.2012.

[38]G.M.Ribeiro and G.Laporte,“An adaptive large neighborhood search heuristic for the cumulative capacitated vehicle routing problem,”Comput.Oper.Res.,vol.39,no.3,pp.728-735,Mar.2012.

[39]S.U.Ngueveu,C.Prins,and R.W.Calvo,“An effective memetic algorithm for the cumulative capacitated vehicle routing problem,”Comput.Oper.Res.,vol.37,no.11,pp.1877-1885,Nov.2010.