Cyber Attack Protection and Control of Microgrids

Md Masud Rana,Li Li,and Steven W.Su

I.INTRODUCTION

THE smart grid can provide an efficient way of supplying and consuming energy by providing two-way energy flow and communication[1].It can integrate multiple renewable distributed energy resources(DERs)which are environment friendly,has low green house emission and is effective to alleviate transmission power losses.The associated connectivity and advanced information/communication infrastructure make the smart grid susceptible to cyber attacks[1],[2].Statistics in the energy sector show that more than 150 cyber attacks happened in 2013 and 79 in 2014[1].As a result,the power outage cost is about$80 billion per year in the USA.Usually,the utility operators amortize it by increasing the energy tariff,which is unfortunately transferred to consumer expenses[3].The renewable microgrid incorporating DERs can be a potential solution,but it needs to be properly monitored as its generation pattern depends on the weather and surrounding conditions.One of the smart grid features is that it can integrate multiple microgrids and monitor them using reliable communication networks.

Since the generation pattern of a microgrid varies on the time-place basis so its operating condition should be closely monitored.Therefore,the microgrid state estimation is an important function in the smart grid energy management system(EMS).As shown in Fig.1 the system state estimation is an essential task for the monitoring and control of the power network.In order to monitor the grid information,the utility company has deployed a set of sensors around the smart grid.The communication infrastructure is used to send grid information from sensors to the EMS.The accurately estimated states can also be used in other functions of EMS such as contingency analysis,bad data detection,energy theft detection,stability analysis,and optimal power dispatch[4].

However,it is not economical or even infeasible to measure all states,so the state estimation is also a key task in this regard[5].More importantly,cyber attacks can cause major social,economical and technical problems such as blackouts in power systems,tampering of smart meters reading and changing the forecasted load pro files[3].These types of catastrophic phenomena are much easier to be committed in microgrids,so they create much more serious problems in the smart grid compared with the traditional grid[6].Therefore,the system state estimation under cyber attacks for smart grids has drawn significant interests in the energy industry and signal processing based information and communication societies.

Many studies have been carried out to investigate the cyber attacks in smart grid state estimations.To begin with,most of the state estimation methods use the weighted least squared(WLS)technique under cyber attacks[7]-[9].Chi-Square detector is also used to detect those attacks.Even though this approach is easy to be implemented for nonlinear systems,it is computationally intensive and it cannot eliminate the attacks properly[5],[7].To this end,the WLS basedl1optimization method is explored in[4].Furthermore,a new detection scheme to detect the false data injection attack is proposed in[2].It employs a Kullback-Leibler method to calculate the distance between the probability distributions derived from the observation variations.A sequential detection of false data injection in smart grids is investigated in[2].It adopts a centralized detector based on the generalized likelihood ratio and cumulative sum algorithm.Note that this detector usually depends on the parametric inferences so is inapplicable to the nonparametric inferences[10].A semide finite programming based AC power system state estimation is proposed in[11].Thereafter,a Kalman filter(KF)based microgrid energy theft detection algorithm is presented in[3].

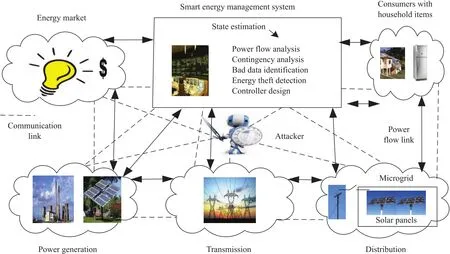
Fig.1. Flow of electricity and information between different sections of smart grid[3].

A lot of efforts have been devoted towards the power system state estimation under the condition of unreliable communication channels.Generally,the attackers have limited attacking energy to jam the channel in order to achieve the desired goals[12].So,the sensor data scheduling for state estimation with energy constraints is studied in[13].In this research,the sensor has to decide whether to send its data to a remote estimator or not based on its energy and estimation error covariance matrix.This idea is further extended in[14],where both the sensor and attacker have energy constraints for sending information.The considered attack is on the communication channel between a sensor and a remote estimator.Basically,the sensor aims to minimize the average estimation error covariance matrix,while attackers try to maximize it.So,an iterative game theory is used to solve the optimization problem.Due to the motivation of unknown attacking patterns,authors in[12],[15]investigated how the attacker can design the attacking policy so the estimation performance can be deteriorated.Then the average estimation error covariance based optimal scheduling strategy is proposed to avoid such kind of attacks.

Many feedback control algorithms have been proposed to regulate the system.The linear quadratic Gaussian(LQG)based detecting techniques for cyber integrity attacks on the sensors of a control system is proposed in[12],[16].It shows that the residual error based chi-squared detection technique is not suitable when the attacker does not know the system dynamics.Based on this analysis,they consider the cyber attack model as an i.i.d(independent,identically distributed)Gaussian distribution,and then the LQG objective function is modified.At the end,they developed a sufficient condition to detect the false alarm probability and proposed an optimization algorithm to minimize it.In[17],a new strategy is recommended for designing a communication and control infrastructure in a distribution system based on the virtual microgrid concept.It is shown in[18],[19]that designing a state feedback control framework for a general case of polynomial discrete-time system is quite challenging because the solution is non-convex.Thus,the convex optimization based controller design has gained growing interest in the research community.

The key contributions of this paper are summarized as follows:

1)A microgrid incorporating multiple distributed energy resources(DERs)is modeled as a discrete time linear statespace equation considering the uncertainty and cyber attack in the measurement.

2)A recursive systematic convolutional(RSC)code is proposed to mitigate the impairments and introduce redundancy in the system states.The log maximum a posterior is adopted to recover the state information which is affected by random noises and cyber attacks.

3)After estimating the system states,a feedback control strategy for voltage regulation of the microgrid is proposed based on semide finite programming.This proposed control scheme acts as a precursor in terms of network stability and the operation of DERs.

The remainder of this paper is organized as follows.A microgrid system model is presented in Section II.The observation model and cyber attack process are described in Section III.Moreover,the KF based dynamic state estimation is described in Section IV.The proposed control technique is derived in Section V,followed by the simulation results and discussions in Section VI.Finally,the paper is wrapped up with conclusions and future work in Section VII.

Notations:Bold face lower and upper case letters are used to represent vectors and matrices,respectively;x′denotes the transpose ofx,E(·)denotes the expectation operator andIis the identity matrix.

II.MICROGRID SYSTEM MODEL

The consideredNmicro-sources in this study are connected to the main grid.For simplicity,we assume thatN=4 solar panels are connected through the IEEE-4 bus test feeder as shown in Fig.2[20],[21].Here,the input voltages are denoted byvp=(vp1vp2vp3vp4)′,wherevpiis theith DER input voltage.The four micro-sources are connected to the power network at the corresponding points of common coupling(PCCs)whose voltages are denoted byvs=(v1v2v3v4)′,whereviis theith point of common coupling(PCC)voltage.

Now by applying Laplace transformation,the nodal voltage equation can be obtained:

Fig.2. Micro-sources are connected to the power network[21].

whereLc=diag{Lc1,Lc2,Lc3,Lc4}andY(s)is the admittance matrix of the entire power network incorporating four micro-sources[21].Now we can convert the transfer function form into the linear state-space model[21].The discrete-time linear dynamic system can be derived as follows:

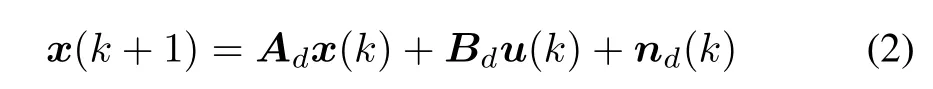
wherex(k)=vs-vrefis the PCC state voltage deviation,vrefis the PCC reference voltage,u(k)=vp-vprefis the DER control input deviation,vprefis the reference control effort,nd(k)is the zero mean process noise whose covariance matrix isQn,the state matrixAd=I+AΔtand input matrixBd=BΔtwith

and Δtis the discretization parameter.For discretizing a continuous-time system into a discrete-time system,there are several techniques available in the literature such as traditional approximation method,delta operator and shift operator[22]-[25].Similar to[22],[25],this paper adopts the traditional approximation method ignoring discretization errors.In the following section,the observation model and attack process is explored.

III.OBSERVATION MODEL ANDCYBER ATTACK

The measurements of the microgrid states are obtained by a set of sensors and can be modeled as follows:

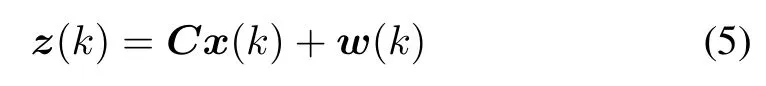
wherez(k)is the measurements,Cis the measurement matrix andw(k)is the zero mean sensor measurement noise whose covariance matrix isRw.Generally,the objective of attackers is to insert false data into the observations as follows:

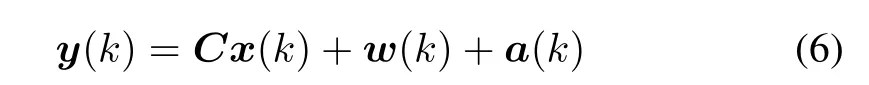
wherea(k)is the false data inserted by the attacker[1]-[3].The attackers have complete access to the system infrastructure so that they can hijack,record and manipulate data according to their best interest.In this paper,the cyber attack pattern is similar to those illustrated in[1],[2],[26].Fig.3 shows the observation model and cyber attack process in the context of smart grid state estimations.

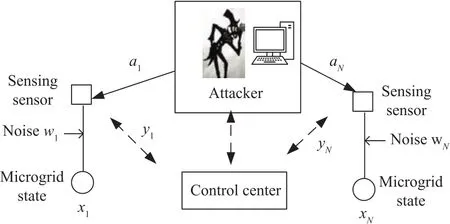
Fig.3.Observation model with cyber attack in the microgrid.

To secure the system states,in the signal processing research community,the channel code is used.Motivated by the convolutional coding concept[27],[28],the microgrid statespace and observation models are regarded as the outer code.Then,the standard uniform quantizer performs quantization to get the sequence of bitsb(k).b(k)is encoded by RSC channel code which is regarded as the inner code.The main reason for using RSC code is to mitigate impairments and introduce redundancy in the system to protect the grid information.Generally speaking,RSC code is characterized by three parameters:the codeword lengthn,the message lengthl,and the constraint lengthm,i.e.,(n,l,m).The quantityl/nrefers to the code rate which indicates the amount of parity bits added to the data stream.The constraint length speci fiesm-1 memory elements which represents the number of bits in the encoder memory that affects the RSC generation output bits.If the constraint lengthmincreases,the encoding process intrinsically needs a longer time to execute the logical operations.Other advantages of the RSC code compared with the convolutional and turbo encoder include its reduced computation complexity,systematic output features and no error floor[29].From this point of view,this paper considers a(2,1,3)RSC code and(1 0 1,1 1 1)code generator polynomial in the feedback process.According to the RSC features,the code rate is 1/2 and there are two memories in the RSC process.As shown in Fig.4,this RSC code produces two outputs and can convert an entire data stream into one single codeword[30].The codeword is then passed through the binary phase shift keying(BPSK)to obtains(k).s(k)is passed through the additive white Gaussian noisy(AWGN)channel.To illustrate,Fig.4 shows the proposed cyber attack protection procedure in the context of smart grids.

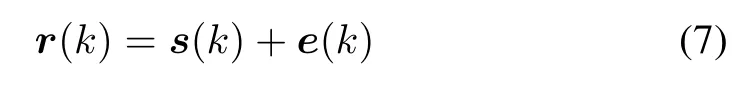
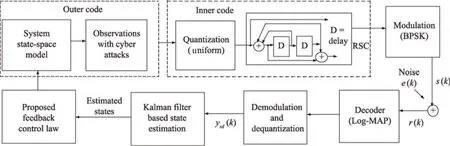
Fig.4. An illustration of the cyber attack protection in smart grids.

IV.PROPOSED FRAMEWORK FOR CYBER ATTACK MINIMIZATION IN SMART GRIDS

The proposed framework uses the KF to estimate the system states in the context of smart grids.The KF operates recursively on observation information to produce the optimal state estimation.Generally,the forecasted system state estimate is expressed as follows[31]:

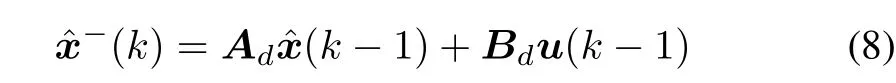
whereˆx(k-1)is the estimated state of the last step.Then the forecasted error covariance matrix is given by:

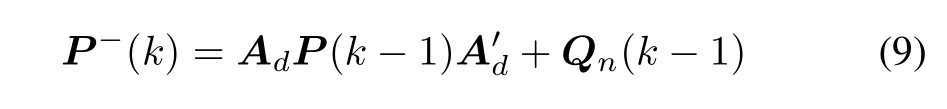
whereP(k-1)is the estimated error covariance matrix of the last step.The observation innovation residuald(k)is given by:

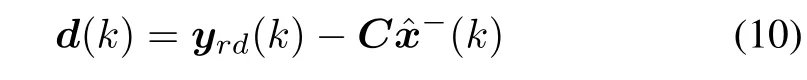
whereyrd(k)is the dequantized and demodulated output bit sequence.The Kalman gain matrix can be written as:

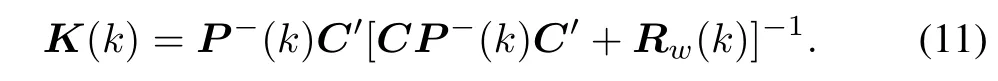
The updated state estimation is given by:

Finally,the updated estimated error covariance matrixP(k)is expressed as follows:

After estimating the system state,the proposed control strategy is applied for regulating the microgrid states as shown in the next section.

V.PROPOSED OPTIMAL FEEDBACK CONTROLLER

In the simulation section,it has been shown that the proposed method is able to well estimate the system states.So,here we assume the microgrid state information is available.In order to regulate the microgrid states,define the following feedback control law[32]-[34]:

by minimizing the following cost function:

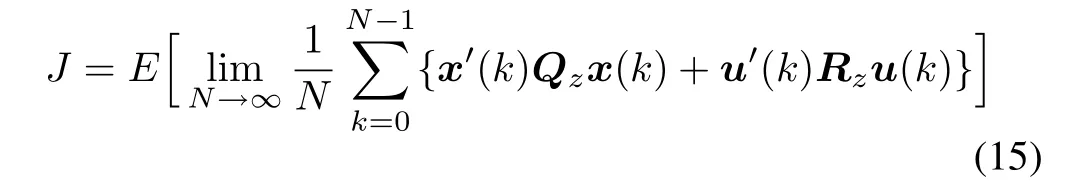
whereE(·)denotes the expectation operator andFis the state feedback gain matrix,QzandRzare positive-de finite state weighting matrix and control weighting matrix.

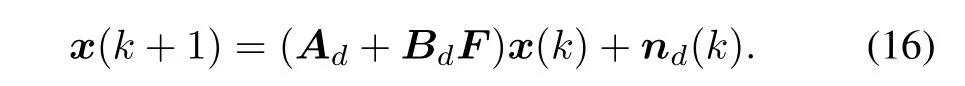
Then the closed loop system is:By using(14)and standard trace operator(m′Dn=tr[Dnm′]),(15)can be expressed as:

Then(18)can be written as follows:

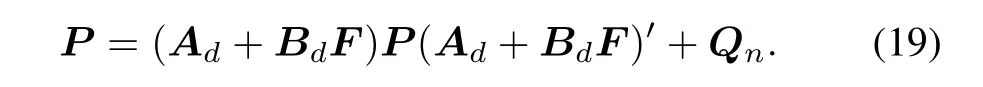
Now one can consider the following inequality,

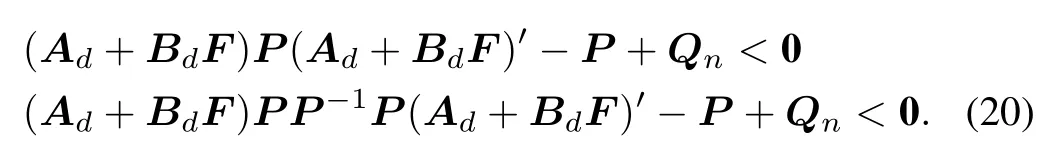
Now one can introduce a new variableH=FPand rewrite the(20)as follows:

Now according to the Schur’s complement,(21)can be transformed into the following form:

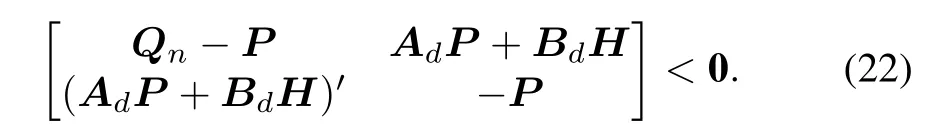
From(17),FandPcan be found by minimising the following expression:

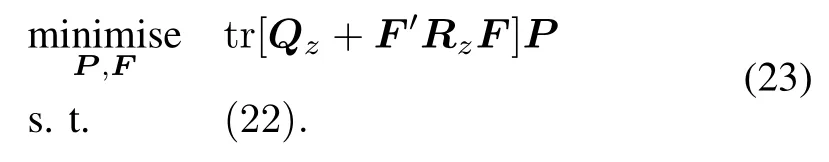
Based on theH=FP,(23)can be transformed as follows:

According to the Schur’s complement,we can rewrite(25)as follows:

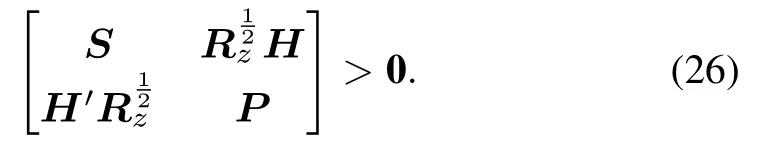
Then we can formulate the proposed optimization problem as follows[30]:

Finally,the feedback gain matrix is computed as:

The proposed convex problem can be solved effectively and efficiently using a number of available softwares such as YALMIP[35].

VI.PERFORMANCE EVALUATION

In this section,we evaluate the performance of the proposed approaches under cyber attacks in smart grids.An overall system level diagram for system state estimation and control is illustrated in Fig.5.After sensing and quantizing the system states,RSC code is proposed to add redundancy into the data stream in a controlled manner to give the Log-MAP decoder to correct errors at EMS.Once the estimated system states are obtained,a semide finite programming based optimal feedback controller is proposed to regulate the system states[30].The simulation is performed using the microgrid connected to IEEE 4-bus distribution feeder.The simulation parameters are summarized in Table I.

The mean squared error(MSE)versus signal-to-noise ratio(SNR)is presented in Fig.6.It can be observed that the proposed method provides significant performance improvement compared with the existing method[1].The reason is that the RSC code is used to protect the system from cyber attacks and noises by adding redundancy in the system states.It can also protect the state information from the unreliable lossy communication networks.Furthermore,the Log-MAP decoding can also facilitate the accurate extraction of the system state.For better visualization of the cyber attack,the states versus time step are illustrated in Figs.7-10.It can be observed and expected that the cyber attack still affects the system states seriously when the existing method is used to estimate system states[1].In other words,there is a significant fluctuation due to the random noises and cyber attacks.Interestingly,the proposed RSC based cyber attack protection technique can tolerate the system impairments by introducing redundancy and protection in the system states.As a result,the proposed method can estimate microgrid states accurately even if there are cyber attacks and noises.

Fig.5. System level diagram for system state estimation and control.

TABLE IPARAMETERS FOR THE SIMULATION

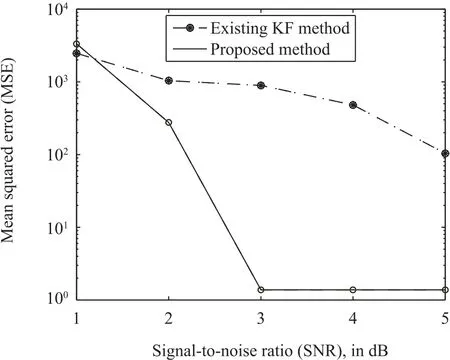
Fig.6.MSE versus SNR performance comparison using microgrid.

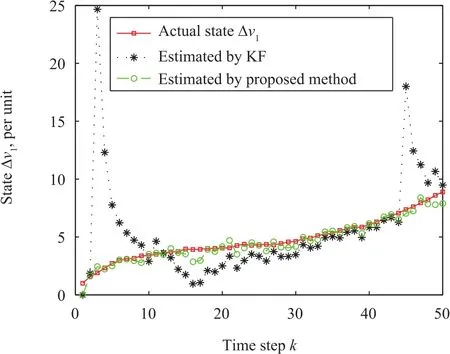
Fig.7. State trajectory of Δv1and its estimate.

Fig.8. State trajectory of Δv2and its estimate.

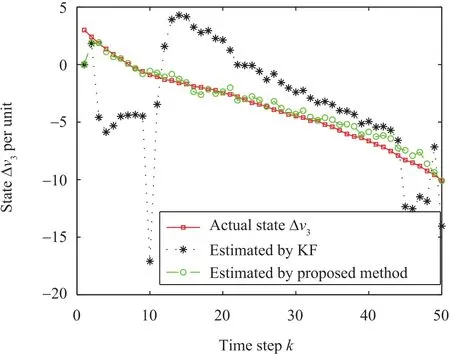
Fig.9. State trajectory of Δv3and its estimate.

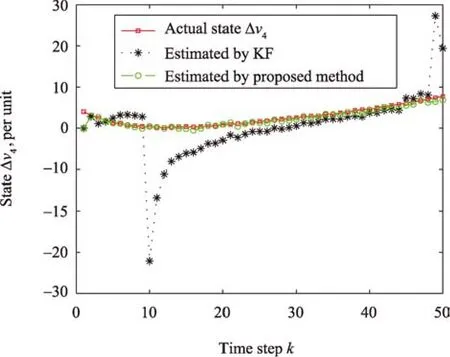
Fig.10.State trajectory of Δv4and its estimate.

Fig.11.Controlling the states trajectory.

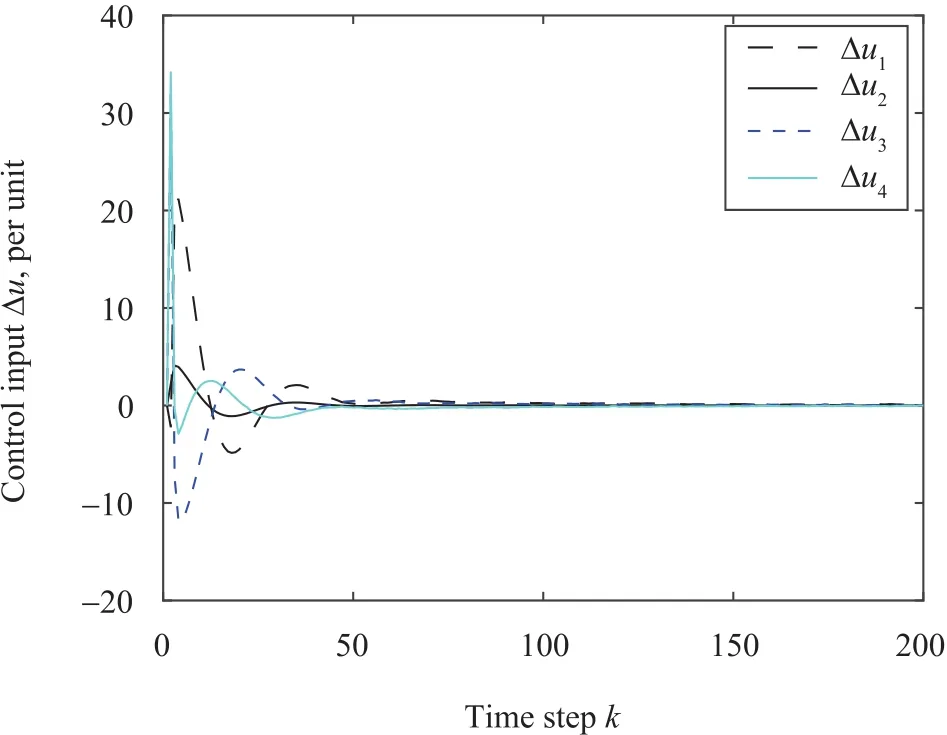
Fig.12.Control input trajectory.

Unfortunately,it is noticed that the actual PCC state deviations increase dramatically(Figs.7-10),which is very dangerous in terms of network stability and microgrid operation.Thus,it is necessary to apply a suitable control technique,so that the PCC voltage deviations are driven to zero.After applying the proposed control method to the microgrid connected to the IEEE 4-bus distribution system,it can be seen from Figs.11 and 12 that the proposed controller is able to keep the voltage deviations to zero by the timek=200,which acts as a precursor in terms of network stability and proper operation of microgrids.Besides,the corresponding control input of each DER is shown in Fig.12,which implies that it requires a small amount of control input.

VII.CONCLUSION

This paper proposes a cyber attack minimization based dynamic state estimation technique and feedback control algorithm in smart grids.An RSC coded cyber attack protection technique is proposed to add redundancy in the system states.Then a Log-MAP decoding can assist to extract the system states from the received signal which is polluted by random noises and cyber attacks.In order to regulate the voltage deviation,this study proposes a semide finite programming based optimal feedback control method.The effectiveness of the developed approaches is verified by numerical simulations.These findings can help to design the future smart control center under cyber attacks.Consequently,it is encouraged to use an environmentally friendly renewable microgrid and the utility operator can monitor and control the power network properly.In the future work,packet losses and delay will be investigated in terms of system performance.

[1]D.B.Rawat and C.Bajracharya,“Detection of false data injection attacks in smart grid communication systems,”IEEE Signal Process.Lett.,vol.22,no.10,pp.1652-1656,Oct.2015.

[2]S.Li,Y.Y.lmaz,and X.D.Wang,“Quickest detection of false data injection attack in wide-area smart grids,”IEEE Trans.Smart Grid,vol.6,no.6,pp.2725-2735,Nov.2015.

[3]M.Esmalifalak,G.Shi,Z.Han,and L.Y.Song,“Bad data injection attack and defense in electricity market using game theory study,”IEEE Trans.Smart Grid,vol.4,no.1,pp.160-169,Mar.2013.

[4]K.C.Sou,H.Sandberg,and K.H.Johansson,“On the exact solution to a smart grid cyber-security analysis problem,”IEEE Trans.Smart Grid,vol.4,no.2,pp.856-865,Jun.2013.

[5]M.Esmalifalak,H.Nguyen,R.Zheng,and Z.Han,“Stealth false data injection using independent component analysis in smart grid,”inProc.Int.Conf.Smart Grid Communications,Brussels,Belgium,2011,pp.244-248.

[6]S.A.Salinas,and P.Li,“Privacy-preserving energy theft detection in microgrids:A state estimation approach,”IEEE Trans.Power Syst.,vol.31,no.2,pp.883-894,Mar.2016.

[7]G.Hug and J.A.Giampapa,“Vulnerability assessment of AC state estimation with respect to false data injection cyber-attacks,”IEEE Trans.Smart Grid,vol.3,no.3,pp.1362-1370,Sep.2012.

[8]A.Alimardani,F.Therrien,D.Atanackovic,J.Jatskevich,and E.Vaahedi,“Distribution system state estimation based on nonsynchronized smart meters,”IEEE Trans.Smart Grid,vol.6,no.6,pp.2919-2928,Nov.2015.

[9]S.Meliopoulos,R.K.Huang,E.Polymeneas,and G.Cokkinides,“Distributed dynamic state estimation:Fundamental building block for the smart grid,”inProc.Power&Energy Society General Meeting,Denver,CO,USA,2015,pp.1-6.

[10]C.J.Gu,P.Jirutitijaroen,and M.Motani,“Detecting false data injection attacks in AC state estimation,”IEEE Trans.Smart Grid,vol.6,no.5,pp.2476-2483,Sep.2015.

[11]Y.Weng,Q.Li,R.Negi,and M.Ilic´,“Distributed algorithm for SDP state estimation,”inProc.IEEE PES Innovative Smart Grid Technologies,Washington,DC,USA,2013,pp.1-6.

[12]H.Zhang,P.Cheng,L.Shi,and J.M.Chen,“Optimal denial-ofservice attack scheduling with energy constraint,”IEEE Trans.Automat.Control,vol.60,no.11,pp.3023-3028,Nov.2015.

[13]L.Shi,P.Cheng,and J.M.Chen,“Sensor data scheduling for optimal state estimation with communication energy constraint,”Automatica,vol.47,no.8,pp.1693-1698,Aug.2011.

[14]Y.Z.Li,L.Shi,P.Cheng,J.M.Chen,and D.E.Quevedo,“Jamming attacks on remote state estimation in cyber-physical systems:A gametheoretic approach,”IEEE Trans.Automat.Control,vol.60,no.10,pp.2831-2836,Oct.2015.

[15]H.Zhang,P.Cheng,L.Shi,and J.M.Chen,“Optimal dos attack policy against remote state estimation,”inProc.52nd Annu.Conf.Decision and Control,Firenze,Italy,2013,pp.5444-5449.

[16]Y.L.Mo,R.Chabukswar,and B.Sinopoli,“Detecting integrity attacks on SCADA systems,”IEEE Trans.Control Syst.Technol.,vol.22,no.4,pp.1396-1407,Jul.2014.

[17]S.A.Are fifar,A.R.I.Mohamed,T.El-Fouly,“Optimized multiple microgrid-based clustering of active distribution systems considering communication and control requirements,”IEEE Trans.Ind.Electron.,vol.62,no.2,pp.711-723,Feb.2015.

[18]S.Saat,S.K.Nguang,J.Wu,and G.B.Zeng,“Disturbance attenuation for a class of uncertain polynomial discrete-time systems:An integrator approach,”inProc.12th Int.Conf.Control Automation Robotics&Vision,Guangzhou,China,2012,pp.787-792.

[19]N.Azman,S.Saat,and S.K.Nguang,“Nonlinear observer design with integrator for a class of polynomial discrete-time systems,”inProc.Int.Conf.Computer,Communications,and Control Technology,Kuching,Malaysia,2015,pp.422-426.

[20]H.J.Li,F.X.Li,Y.Xu,D.T.Rizy,and J.D.Kueck,“Adaptive voltage control with distributed energy resources:Algorithm,theoretical analysis,simulation,and field test verification,”IEEE Trans.Power Syst.,vol.25,no.3,pp.1638-1647,Aug.2010.

[21]H.S.Li,L.F.Lai,and H.V.Poor,“Multicast routing for decentralized

control of cyber physical systems with an application in smart grid,”IEEE J.Sel.Areas Commun.,vol.30,no.6,pp.1097-1107,Jul.2012.

[22]E.Ghahremani and I.Kamwa,“Online state estimation of a synchronous generator using unscented Kalman filter from phasor measurements units,”IEEE Trans.Energy Conv.,vol.26,no.4,pp.1099-1108,Dec.2011.

[23]D.Buchstaller,E.C.Kerrigan,and G.A.Constantinides,“Sampling and controlling faster than the computational delay,”IET Control Theory Appl.,vol.6,no.8,pp.1071-1079,May2012.

[24]H.J.Yang,Y.Q.Xia,P.Shi,and M.Y.Fu,“A novel delta operator Kalman filter design and convergence analysis,”IEEE Trans.Circ.Syst.I:Reg.Pap.,vol.58,no.10,pp.2458-2468,Oct.2011.

[25]T.J.Sui,K.Y.You,M.Y.Fu,and D.Marelli,“Stability of MMSE state estimators over lossy networks using linear coding,”Automatica,vol.51,pp.167-174,Jan.2015.

[26]S.Ntalampiras,“Detection of integrity attacks in cyber-physical critical infrastructures using ensemble modeling,”IEEE Trans.Ind.Inf.,vol.11,no.1,pp.104-111,Feb.2015.

[27]Y.Jing,A Practical Guide to Error-Control Coding Using MATLAB.Boston,London,UK:Artech House,2010.

[28]S.P.Gong,H.S.Li,L.F.Lai,and R.C.Qiu,“Decoding the‘nature encoded’messages for distributed energy generation control in microgrid,”inProc.IEEE Int.Conf.Communications,Kyoto,Japan,2011,pp.1-5.

[29]C.Vlaˇdeanu and S.El Assad,Nonlinear Digital Encoders for Data Communications.New York,USA:John Wiley&Sons,2014.

[30]M.M.Rana,L.Li,and S.W.Su,“Cyber attack protection and control in microgrids using channel code and semide finite programming,”inProc.Power and Energy Society General Meeting,Boston,MA,USA,2016,pp.1-5.

[31]D.Simon,Optimal State Estimation:Kalman,H In finity,and Nonlinear Approaches.New Jersey,USA:John Wiley&Sons,2006.

[32]A.K.Singh,R.Singh,and B.C.Pal,“Stability analysis of networked control in smart grids,”IEEE Trans.Smart Grid,vol.6,no.1,pp.381-390,Jan.2015.

[33]C.Olalla,R.Leyva,A.El Aroudi,and I.Queinnec,“Robust LQR control for PWM converters:An LMI approach,”IEEE Trans.Ind.Electron.,vol.56,no.7,pp.2548-2558,Jul.2009.

[34]M.Fardad and M.R.Jovanovic´,“On the design of optimal structured and sparse feedback gains via sequential convex programming,”inProc.American Control Conf.,2014,Portland,OR,USA,pp.2426-2431.

[35]J.Lo¨fberg,“YALMIP:A toolbox for modeling and optimization in MATLAB,”inProc.IEEE Int.Symp.Computer Aided Control Systems Design,Taipei,China,2004,pp.284-289.