Robust H∞Load Frequency Control of Multi-area Power System With Time Delay:A Sliding Mode Control Approach

Yonghui Sun,Yingxuan Wang,Zhinong Wei,Guoqiang Sun,and Xiaopeng Wu

I.INTRODUCTION

LOAD frequency control(LFC)is important and necessary in electric power system operation,which could help damp frequency and voltage oscillations originated from load variations or sudden changes in load demands[1]-[2].When the system is subject to disturbances or sudden changes in load demands,the input mechanical power to the generators is employed to control the frequency of the output electrical power and to maintain the power exchange between different control areas as per scheduled values during normal operation.Therefore,a well designed and operated power system should be able to cope with changes in the load and system disturbances,and it should provide acceptably high level of power quality while maintaining both voltage and frequency within tolerable limits.

Until now,lots of classical and advanced techniques have been proposed to solve the LFC problems for single or interconnected power system,e.g.,proportional integral(PI)control approach[3]was first proposed to solve the LFC problems.In[4],a robust decentralized proportional-integral control design was proposed for LFC of a multi-area power system.In[5],considering the parameter uncertainties,a robust decentralized controller was designed for multi-area power system based on the Riccati-equation approach.In[6],based on the concept of active disturbance rejection control,a robust decentralized LFC algorithm was proposed for an interconnected three-area power system using frequency-domain analysis.In[7],the adaptive control scheme was proposed to deal with the changes of system parameters under the LFC strategies.With the emerging intelligent control techniques,some hybrid controllers can drive better desirable responses than the traditional LFC.The intelligent PILFC using genetic algorithm[8],bat inspired algorithm[9],fuzzy logic[10]and neural network[11]have been adopted to consider the effect of uncertainty and disturbances in the power system model.For the other related results,please refer to[12],and the references therein.

On the other hand,as time delays are mainly derived from the local measurement device,for traditional power system,time delays are too small which can be ignored in most cases[13],[14].However,with the development of power system,remote signals have become available as feedback signals to design modern power system.Therefore,time delays are becoming more and more ubiquitous and have become a source of instability and performance deterioration in system.In[15],two robust decentralized PI controller designs were proposed for LFC of power system with communication delays.In[16],the authors presented a load frequency control method based on linear matrix inequalities(LMIs),where a robust controller was proposed in the face of delayed control signals.In[17],the authors considered the delay-dependent stability of load frequency control scheme based on Lyapunov theory,where a delay-dependent criterion was developed.In[18],the authors considered the LFC problem with communication delays,where a delay-dependent two-termH∞controller design was proposed using LMIs.In[19],a delay-dependent robust method was proposed for analysis/synthesis of a PID-type LFC scheme considering time delays,where a new way to assess robustness against delays and estimate delay margins was also presented.However,with the increasing size,changing structure and complexity of interconnected power system[20],[21],LFC problem is becoming much more significant today,in order to get fast response,insensitivity to variation in plant parameters and complete rejection of external perturbations,some other effective robust control methods should be explored and developed.

Since the 1970s,variable structure control has attracted signi ficant attentions in the control community.As a special type of variable structure controls,sliding mode control(SMC)is assumed to provide an effective alternative to deal with the robust issues of dynamic systems.The main feature of SMC is claimed to result in system performance including fast response,easy realization,insensitivity to variation in plant parameters and complete rejection of external perturbations,for some more detailed discussions,please refer to[22]-[27]and the references therein.In SMC,the behavior of the closedloop system is determined by a submanifold in the state space,named as the sliding surface,the goal is to drive the system trajectory to reach the sliding surface and then to stay on it.In[28],the second-order sliding mode control design problem was investigated for nonlinear system with uncertainties bounded by positive functions.Considering its robust properties,SMC has been utilized for analyzing and controlling of complex power system in the past few years.In[29],by using SMC approach,the authors presented LFC for multi-area power system with unmatched uncertainties.In[30],the authors considered LFC by neural-network-based integral sliding mode for power system with wind turbines.For the other related results,please refer to[31]-[32]and the references therein.However,most of the above mentioned results ignored the time delay in multi-area power system,and there are few results considering time delay in the design of switching surface in SMC,where the fast response and robust performance cannot be guaranteed.Furthermore,to the best of the authors’knowledge,there are also few results considering SMLFC of delayed power system with stochastic disturbances,therefore,in this paper,the attention is paid to the robustH∞SMLFC of multi-area power system with time delay.

The rest of the paper is organized as follows.In Section II,the LFC problem for multi-area power system is presented,a useful lemma is also introduced in advanced.In Section III,a new switching surface considering time delay is designed for each area of power system.In Section IV,the sliding mode controller is designed to drive the system trajectory to reach the sliding surface and stay on it.In Section V,some simulation results are provided to show the feasibility of the developed results.At last,this paper is completed with a conclusion.

II.MODEL DESCRIPTION

It is known that power system is a complex nonlinear dynamic system,especially the multi-area power system,however,the linearized model is permissible in the LFC problem due to only small changes in load are expected during its normal operation.In this paper,by using the SMC approach,the robustH∞LFC problem for multi-area power system with time delay is discussed in detail.For convenience,a two-area interconnected power system with time delay is provided as an example to illustrate the LFC problem for multi-area power system,which is shown in Fig.1.

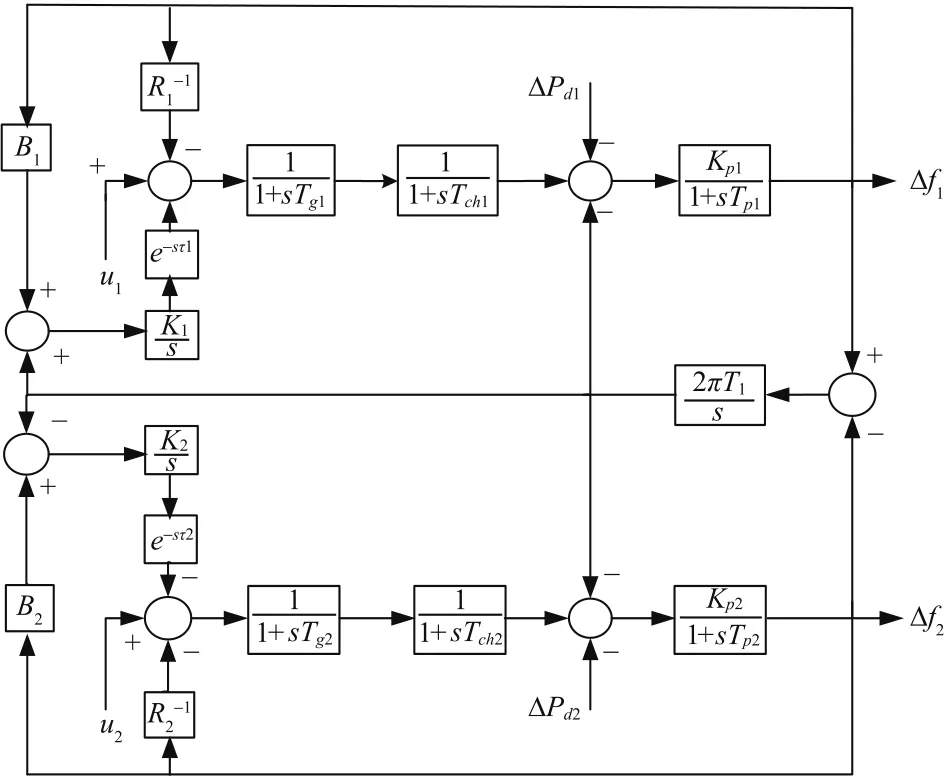
Fig.1.A typical two-area LFC power system.

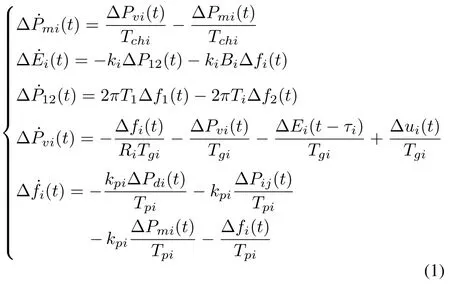
The dynamic model can be described by

wherei,j=1,2,i/=j,and ΔP12=-ΔP21.

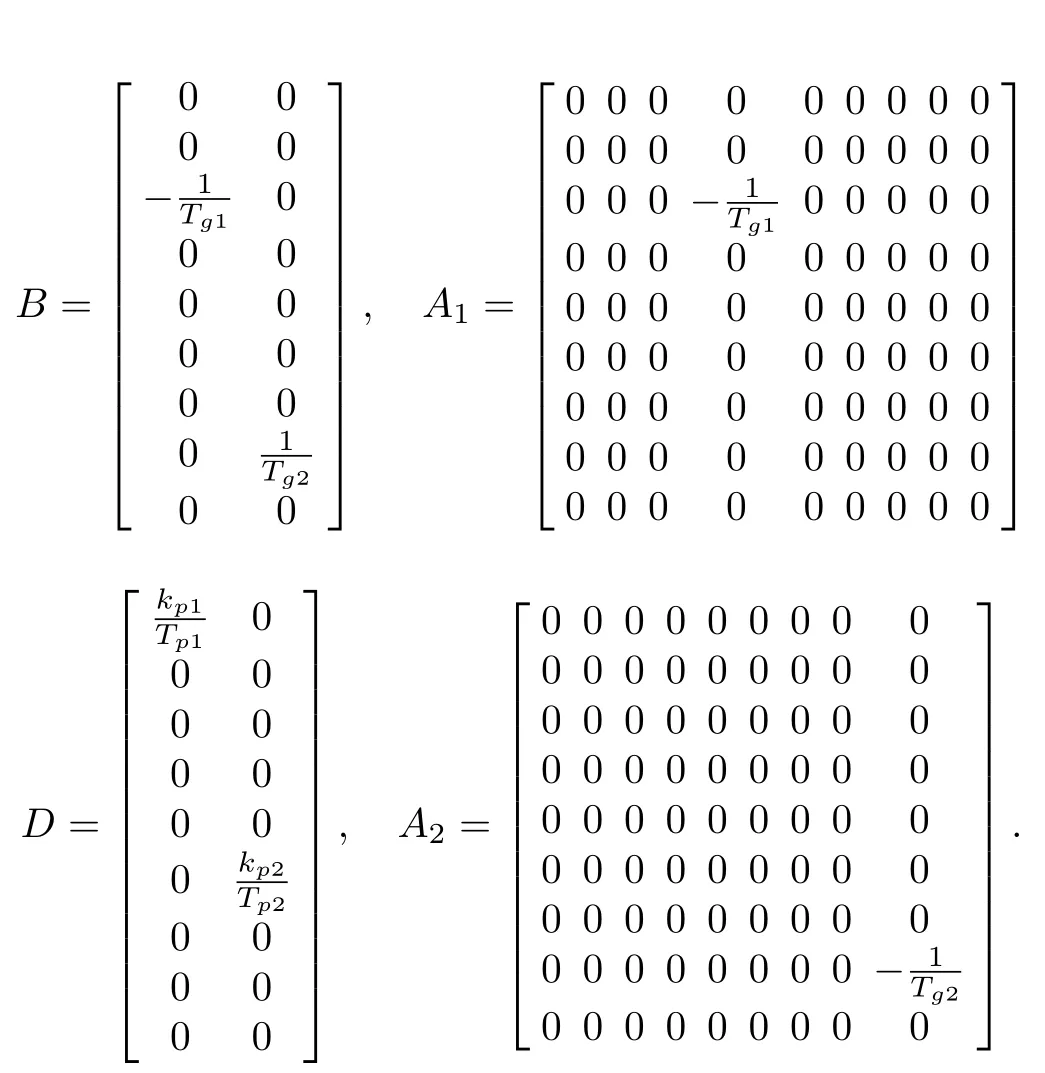
De fine the state vector asx(t)=[Δf1,ΔPm1,ΔPv1,ΔE1,ΔP12,Δf2,ΔPm2,ΔPv2,ΔE2]T,then system(1)can be represented in the following compact form:

wherew(t)is the load disturbance vector de fined asw(t)=ΔPd= [ΔPd1,ΔPd2]T,without loss generality,w(t)is bounded and satis fies‖ΔPd1‖＜h1,‖ΔPd2‖＜h2,h1andh2are two positive constants.τ1andτ2are the transmission delays induced by signals transmitted from different control areas,and system parameters are given by

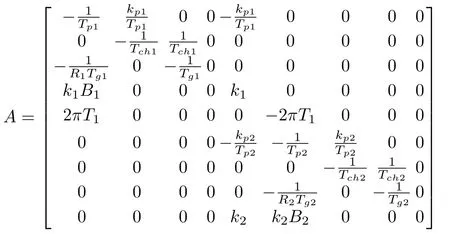
The main purpose of this paper is to consider the robustH∞SMLFC of multi-area power system with time delay and stochastic disturbances,and before presenting the main results,the following useful lemma is introduced in advance.

Lemma 1[33]:For a given symmetric matrixS=,whereS11isr×rdimensional matrix,S11=The following three conditions are equivalent:

III.SWITCHING SURFACE DESIGN

The traditional sliding mode controller design includes two relatively independent parts,the first part is to choose the sliding mode surface for desired performance,and the second part is to design the control law to drive the system trajectory to the surface and maintain motion on it.In this paper,considering the time delay induced by signal transmission between different control areas,in order to enhance the dynamic performance and robustness during the reaching phase,an improved PI switching surface is selected as

whereGandKare constant matrices,andGis selected to ensure matrixGBto be nonsingular.

When the dynamic trajectory reaches the sliding mode,the switching function(3)satis fies the following condition:

Differentiating(3)will yield

Then,by substituting(2)into(5),one has

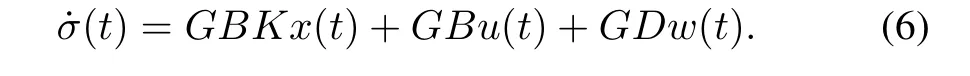
If the dynamic trajectory satis fies(t)=0,the following equivalent controller can be derived when the state trajectory reaches the sliding mode surface

Furthermore,by substituting(7)into system(2),the equivalent dynamic equation in sliding mode can be derived

whereA0=A-BK,D0=D-B(GB)-1GD.Therefore,by using the equivalent controller(7),the LFC for two-area interconnected power system can be derived

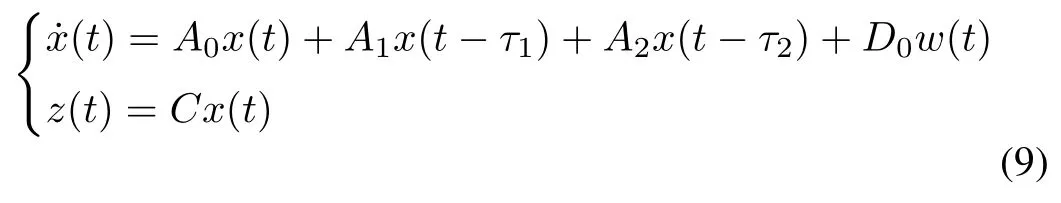
the relationship between interference and output isTwz(s)=C[sI-(A0+BK)-A1e-τ1s-A2e-τ2s]-1D0.Meanwhile,the controller design should meet theH∞performance‖Twz‖∞＜γ,γ ＞0.

Remark 1:Compared to the traditional switching surface designing approaches[29]and[30],in which only the proportional and integral part are included,the priority of the designed switching surface in this paper is that time delay between different control areas is taken into account,two integral parts with the corresponding transmission delays are introduced into the switching surface functional.Therefore,these improvements could be expected to enhance the dynamic performance under the wide area environment.

Now,we are ready to develop the following frequency stabilization result.

Theorem 1:For a prescribed attenuation levelγ＞0,the frequency of controlled interconnected power system(9)is asymptotically stable with‖Twz‖∞＜γ,forτ1＞0,τ2＞0,if there exist matrices 0＜PT=P∈Rn×n,0＜=Q1∈Rn×n,0＜=Q2∈Rn×nand an arbitrary matrixSsatisfying the following LMI:

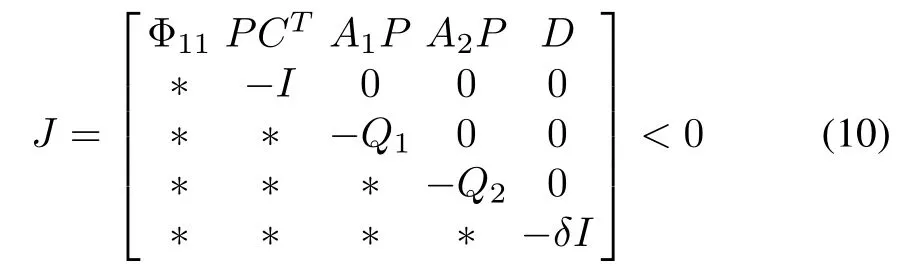
where Φ11=AP+PAT+BS+STBT+Q1+Q2,δ=γ2.Moreover,the gain of the state feedback controller can be calculated byK=SP-1.

Proof:Firstly,consider the stability of controlled interconnected power system(9)withw(t)=0,construct the following Lyapunov functional:

Calculating the derivative of(11)along the trajectory(9),one can get

where

By using Lemma 1,it follows from the LMI condition(10)that Δ＜0,which means˙V＜0.Therefore,it can be concluded that the frequency of controlled multi-area power system(9)is asymptotically stable withw(t)=0.

Furthermore,for a prescribed attenuation levelγ＞0,de fine the following performance index:

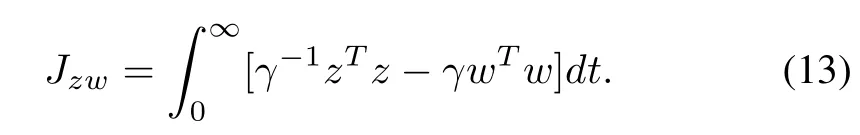
It is noted that ifJzw≤0,then the closed-loop system(9)is robustlyH∞stable satisfying the conditionH∞≤γ.Thus,the next objective is becoming to ensure thatJzw≤0.For zero initial conditionV(0)=0 and sinceV(∞)≥0,one can get

By using Lemma 1,it follows from the condition(10)that Ω＜0,as we knowJzw≤0,we can conclude that the closedloop system(9)is robustlyH∞stable.

Furthermore,the optimal attenuation level can be obtained by solving the following constrained optimization problem:

Then the optimal performance level can be obtained byγ=

Remark 2:Based on the proposed SMLFC scheme,Theorem 1 could guarantee the multi-area power system with time delay and stochastic disturbances to be robustly stable with an optimal attenuation levelγ.Compared to some existing results considering LFC of power system by feedback control approaches[17]-[19],the proposed SMLFC scheme is much robust against the variations in plant parameters and shows complete rejection of external perturbations,which enables to get fast response and good performance.

IV.CONTROL LAW DESIGN

For the controlled multi-area power system(9),the corresponding reachability condition for each area can be described by the following theorem.

Theorem 2:A decentralized switching control law can be designed to guarantee the reaching conditionσi(t)∗i(t)＜0 to be satisfied

where

Proof:Constructing the following Lyapunov function:

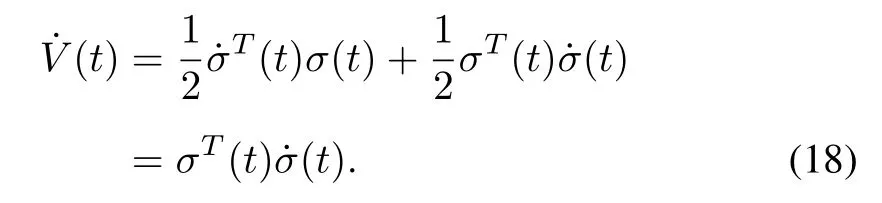
Note that‖ΔPd1‖＜h1,‖ΔPd2‖ ＜h2,then combining(6)and(16),one can further get

The derivative ofV(t)can be calculated by

Therefore,one can conclude that the reaching condition can be ensured by the designed controller(16). ¥

Remark 3:It should be pointed out that in[29],the authors presented LFC for multi-area power system with unmatched uncertainties by SMC approach,and in[30],the authors considered LFC by neural-network-based integral sliding mode for power system with wind turbines.However,both of them ignored time delay in multi-area power system.Furthermore,by taking into account stochastic disturbances induced by the integration of renewable energies,based onH∞control theory,the optimal attenuation level describing the power system tolerant against the fluctuations of renewable power could be obtained.

Remark 4:With more and more renewable energy resources integrated into power grid,the inherent randomness and uncertainties should be paid more attention,some robust control approaches would be utilized and explored for LFC of multiarea power system.Motivated by the idea in[30],some intelligent control approaches combined with the traditional control approaches,such as fuzzy logic control[34]could be an effective way,which are left as the future research directions.

V.SIMULATION AND ANALYSIS

In this section,a two-area interconnected power system is provided to illustrate the effectiveness of the proposed decentralized sliding mode control scheme.Some basic parameters of the system are provided in Table I.

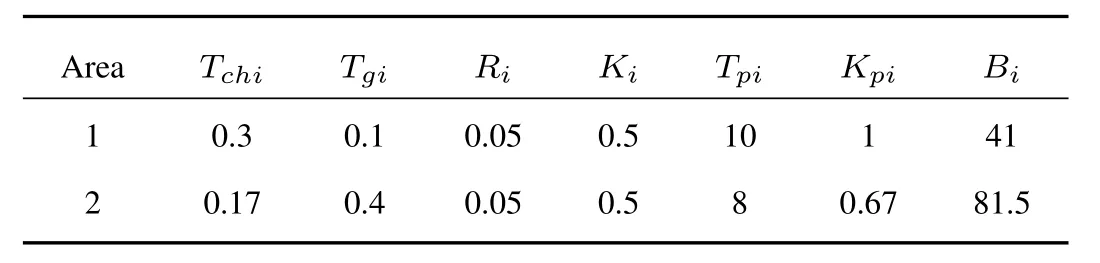
TABLE IPARAMETERS OF TWO-AREA INTERCONNECTED POWER SYSTEM

A.The Open Loop System

First,consider a two-area power system(2)without external control inputu,which only includes an integral partki/s(i=1,2)in each control area.Without loss of generality,time delays in both control areas are manually set asτ1=0.1,τ2=0.2.The block diagram of the open loop system is shown in Fig.1.

Based on the MATLAB/Simulink,the frequency deviation of the two-area power system is illustrated in Fig.2,it follows from the simulation that the frequency deviation of the two-area power system is divergent with the local PI controllerK1=0.5,K2=0.5.

B.The Closed Loop System via SMLFC

In this part,by using the designed sliding mode load frequency controller(16)and the improved switching surface(3),the two-area interconnected power system(2)could be robustly stabilized with an optimal attenuation level.The block diagram of the SMLFC scheme is shown in Fig.3,where Δx1,Δx2are the direct feedback state vectors of each area,respectively,u1andu2are the sliding mode control terms of each area,respectively.It should be pointed out that in the designed SMC controller(16),the first item is utilized to guarantee the state of the system tend towards the equilibrium point on the sliding surface,and the second item is to ensure the system has better performance to suppress the interference.

Fig.2.Frequency deviation curve of the open loop system.

For the given system parameters provided in Table I,by using the MATLAB LMI control toolbox,the stability condition(10)could be verified effectively,the corresponding gain matrix can be calculated by

and the optimal attenuation levelγ=0.1643 could be obtained after solving the constrained optimization problem(15)simultaneously.It follows from Theorem 1 that the controlled interconnected power system(2)could be robustly stabilized via the designed controller.

In the simulation results,without loss of generality,the matrixGis selected as

and the bound of stochastic disturbances is set ash=[0.2,0.3]T.Here,we consider the stochastic disturbances as the step load disturbances,at 10s,the stochastic disturbances in two areas are set as the set load changes ΔPd1= ΔPd2=0.1.Fig.4 shows the frequency derivation of the controlled power system via the proposed control design scheme.It can be observed from Fig.4 that the frequency deviation of the controlled interconnected power system could be stabilized in 4s,and even with the step load disturbances,it can be robustly stabilized in 2s.

Furthermore,in order to demonstrate the robustness of the proposed control design scheme,at 10s,we further consider the control performance with different stochastic disturbances in the two areas ΔPd1=0.1,ΔPd2=0.2,the simulation results are provided in Fig.5,where it can be found that the frequency could be maintained in a tolerable limit time.The switching surface function and the control law of the controller in Area 1 and Area 2 are also presented in Figs.6-9.It can be found from these simulation results that the proposed SMLFC scheme is effective and useful.

Fig.3.The block diagram of SMLFC scheme.

Fig.4.Frequency deviation curve by using SMLFC scheme.

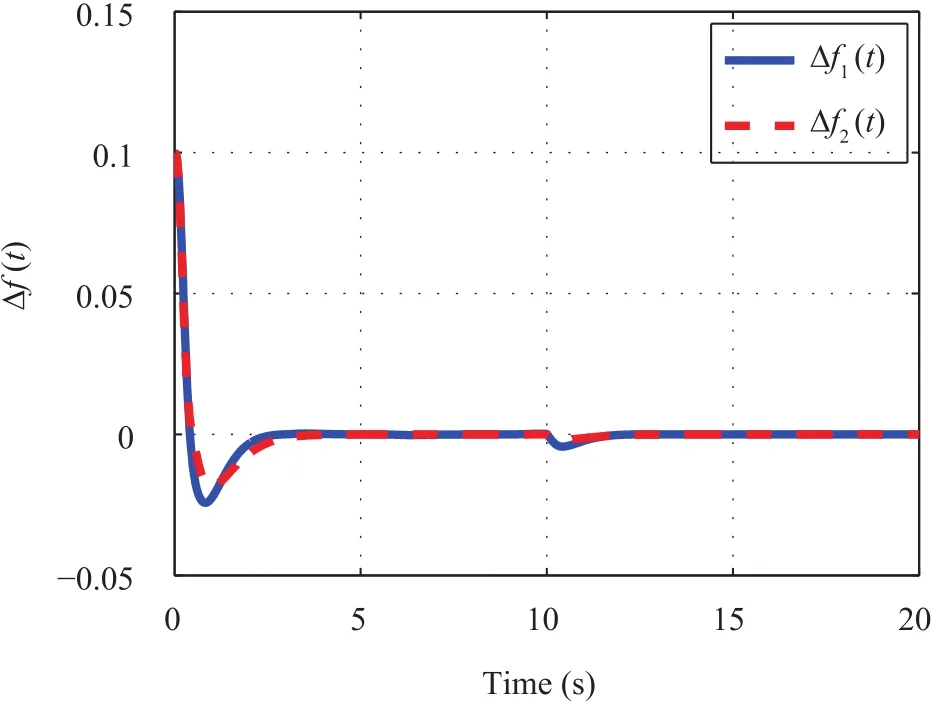
Fig.5.Frequency deviation curve with stochastic disturbances.

Fig.6. Switching surface of σ1.

Fig.7.Switching surface of σ2.

Fig.8.Sliding mode controller u1(t).

Fig.9. Sliding mode controller u2(t).

VI.CONCLUSIONS

In this paper,by taking into account stochastic disturbances,a robust decentralized SMLFC design scheme was proposed for multi-area power system with time delay.In order to get a better control performance,an improved PI switching surface function was constructed,then the robust stability criterion was developed for the multi-area power system with an optimal attenuation level.Furthermore,an SMC law has been proposed to ensure the stability of the closed-loop system,and to drive the state of the controlled system into the prede fined sliding surface.Finally,simulation results on two-area interconnected power system with time delay have been provided to illustrate the effectiveness of the obtained results.

[1]P.Kundur,Power System Stability and Control.New York,USA:McGraw-Hill Press,1994.

[2]P.Ju,E.Handschin,and D.Karlsson,“Nonlinear dynamic load modelling:model and parameter estimation,”IEEE Trans.Power Syst.,vol.11,no.4,pp.1689-1697,Nov.1996.

[3]M.A.Sheirah and M.M.Abd-El-Fattah,“Improved load-frequency self-tuning regulator,”Int.J.Control,vol.39,no.1,pp.143-158,Jan.1984.

[4]M.R.Toulabi,M.Shiroei,and A.M.Ranjbar,“Robust analysis and design of power system load frequency control using the Kharitonov’s theorem,”Int.J.Electr.Power Energy Syst.,vol.55,pp.51-58,Feb.2014.

[5]K.Y.Lim,Y.Wang,and R.Zhou,“Robust decentralised load-frequency control of multi-area power systems,”IEE Proc.-Gener.,Trans.Distrib.,vol.143,no.5,pp.377-386,Sep.1996.

[6]L.L.Dong,Y.Zhang,and Z.Q.Gao,“A robust decentralized load frequency controller for interconnected power systems,”ISA Trans.,vol.51,no.3,pp.410-419,May 2012.

[7]M.Zribi,M.Al-Rashed,and M.Alrifai,“Adaptive decentralized load frequency control of multi-area power systems,”Int.J.Electr.Power Energy Syst.,vol.27,no.8,pp.575-583,Oct.2005.

[8]F.Daneshfar and H.Bevrani,“Multiobjective design of load frequency control using genetic algorithms,”Int.J.Electr.Power Energy Syst.,vol.42,no.1,pp.257-263,Nov.2012.

[9]M.R.Sathya and M.M.T.Ansari,“Load frequency control using Bat inspired algorithm based dual mode gain scheduling of PI controllers for interconnected power system,”Int.J.Electr.Power Energy Syst.,vol.64,pp.365-374,Jan.2015.

[10]K.R.Sudha and R.V.Santhi,“Robust decentralized load frequency control of interconnected power system with generation rate constraint using Type-2 fuzzy approach,”Int.J.Electr.Power Energy Syst.,vol.33,no.3,pp.699-707,Mar.2011.

[11]L.C.Saikia,S.Mishra,N.Sinha,and J.Nanda,“Automatic generation control of a multi area hydrothermal system using reinforced learning neural network controller,”Int.J.Electr.Power Energy Syst.,vol.33,no.4,pp.1101-1108,May 2011.

[12]H.Bevrani,Y.Mitani,and K.Tsuji,“Robust decentralised loadfrequency control using an iterative linear matrix inequalities algorithm,”IEE Proc.-Gener.,Trans.Distrib.,vol.151,no.3,pp.347-354,May 2004.

[13]H.X.Wu,K.S.Tsakalis,and G.T.Heydt,“Evaluation of time delay effects to wide-area power system stabilizer design,”IEEE Trans.Power Syst.,vol.19,no.4,pp.1935-1941,Nov.2004.

[14]X.M.Zhao,Y.H.Sun,C.Yuan,Z.N.Wei,and G.Q.Sun,“Robust load frequency control of multi-area interconnected power system with time delay,”inProc.34th Chinese Control Conf.,Hangzhou,China,2015,pp.8969-8974.

[15]H.Bevrani and T.Hiyama,“Robust decentralised PI based LFC design for time delay power systems,”Energy Convers.Manage.,vol.49,no.2,pp.193-204,Feb.2008.

[16]X.F.Yu and K.Tomsovic,“Application of linear matrix inequalities for load frequency control with communication delays,”IEEE Trans.Power Syst.,vol.19,no.3,pp.1508-1515,Aug.2004.

[17]L.Jiang,W.Yao,Q.H.Wu,J.Y.Wen,and S.J.Cheng,“Delaydependent stability for load frequency control with constant and timevarying delays,”IEEE Trans.Power Syst.,vol.27,no.2,pp.932-941,May 2012.

[18]R.Dey,S.Ghosh,G.Ray,and A.Rakshit,“H∞load frequency control

of interconnected power systems with communication delays,”Int.J.Electr.Power Energy Syst.,vol.42,no.1,pp.672-684,Nov.2012.

[19]C.K.Zhang,L.Jiang,Q.H.Wu,Y.He,and M.Wu,“Delay-dependent robust load frequency control for time delay power systems,”IEEE Trans.Power Syst.,vol.28,no.3,pp.2192-2201,Aug.2013.

[20]F.Wu,P.Ju,X.P.Zhang,C.Qin,G.J.Peng,H.Huang,and J.Fang,“Modeling,control strategy,and power conditioning for direct-drive wave energy conversion to operate with power grid,”Proc.IEEE,vol.101,no.4,pp.925-941,Apr.2013.

[21]Y.H.Sun,X.M.Zhao,N.Li,Z.N.Wei,and G.Q.Sun,“Robust stochastic stability of power system with time-varying delay under Gaussian random perturbations,”Neurocomputing,vol.162,pp.1-8,Aug.2015.

[22]V.Utkin,“Variable structure systems with sliding modes,”IEEE Trans.Automat.Control,vol.22,no.2,pp.212-222,Apr.2017.

[23]Y.Q.Xia and Y.M.Jia,“Robust sliding-mode control for uncertain time-delay systems:an LMI approach,”IEEE Trans.Automat.Control,vol.48,no.6,pp.1086-1091,Jun.2003.

[24]L.G.Wu and D.W.C.Ho,“Sliding mode control of singular stochastic hybrid systems,”Automatica,vol.46,no.4,pp.779-783,Apr.2010.

[25]S.H.Ding and W.X.Zheng,“Nonsingular terminal sliding mode control of nonlinear second-order systems with input saturation,”Int.J.Robust Nonlin.Control,vol.26,no.9,pp.1857-1872,Jun.2016.

[26]H.Y.Li,P.Shi,D.Y.Yao,and L.G.Wu,“Observer-based adaptive sliding mode control for nonlinear Markovian jump systems,”Automatica,vol.64,pp.133-142,Feb.2016.

[27]H.Y.Li,H.J.Gao,P.Shi,and X.D.Zhao,“Fault-tolerant control of Markovian jump stochastic systems via the augmented sliding mode observer approach,”Automatica,vol.50,no.7,pp.1825-1834,Jul.2014.

[28]S.H.Ding,J.D.Wang,and W.X.Zheng,“Second-order sliding mode

control for nonlinear uncertain systems bounded by positive functions,”IEEE Trans.Ind.Electron.,vol.62,no.9,pp.5899-5909,Sep.2015.

[29]Y.Mi,Y.Fu,C.S.Wang,and P.Wang,“Decentralized sliding mode load frequency control for multi-area power systems,”IEEE Trans.Power Syst.,vol.28,no.4,pp.4301-4309,Nov.2013.

[30]D.W.Qian,S.W.Tong,H.Liu,and X.J.Liu,“Load frequency control by neural-network-based integral sliding mode for nonlinear power systems with wind turbines,”Neurocomputing,vol.173,pp.875-885,Jan.2016.

[31]K.Vrdoljak,N.Peric´,and I.Petrovic´,“Sliding mode based loadfrequency control in power systems,”Electr.Power Syst.Res.,vol.80,no.5,pp.514-527,May 2010.

[32]Y.Mi,Y.Fu,D.D.Li,C.S.Wang,P.C.Loh,and P.Wang,“The sliding mode load frequency control for hybrid power system based on disturbance observer,”Int.J.Electr.Power Energy Syst.,vol.74,pp.446-452,Jan.2016.

[33]S.Boyd,L.El Ghaoui,E.Feron,and V.Balakrishnan,Linear Matrix Inequalities in System and Control Theory.Philadelphia,PA,USA:SIAM,1994.

[34]C.D.Li,J.Q.Yi,and G.Q.Zhang,“On the monotonicity of interval type-2 fuzzy logic systems,”IEEE Trans.Fuzzy Syst.,vol.22,no.5,pp.1197-1212,Oct.2014.