Modeling,Optimization,and Control of Solution Purification Process in Zinc Hydrometallurgy

Bei Sun,Chunhua Yang,Hongqiu Zhu,Yonggang Li,and Weihua Gui,

I.INTRODUCTION

ZINC is an important kind of nonferrous metal.Owing to its excellent malleability,abrasive resistance,and anticorrosion property,zinc has been widely used in various departments contributing to national economy,especially in auto industry,construction industry,shipping industry and light industry.However,zinc seldom exists in an elemental form in nature.It normally exists in combination with other base metals such as copper and lead in zinc ores,e.g.,sphalerite,smithsonite,zincite,willemite,hemimorphite,etc.The production of zinc thus involves extraction of special high grade(SHG,99.995%purity)metallic zinc from these intricately composed zinc ores.

Zinc hydrometallurgy is the main approach in zinc production(Fig.1)[1].More than 80%of the world’s production of zinc is obtained by the Roasting-Leaching-Electrowinning(RLE)method and its varieties[2].At present,the most advanced zinc hydrometallurgy technology is known as the atmospheric direct leaching technology[3].A zinc hydrometallurgy process generally contains three major steps,i.e.,leaching,solution purification,and electrowinning,and among these,solution purification holds a critical function.For the impurity of zinc ores and the“incompletely selective”nature of leaching process,both zinc ions and ions of the associated metals are liberated,and enter into the pregnant leaching solution.The presence of these impurities would cause large drops of current efficiency during electrowinning in which metallic zinc is recovered,resulting in severe energy wastage and degradation of product quality[4].The function of solution purification,which serves as a link between leaching and electrowinning,is precisely to reduce the concentration of the impurities to acceptable ranges.

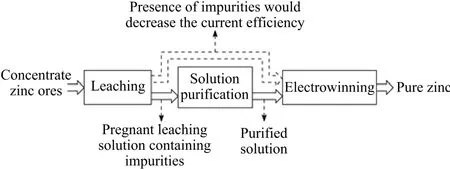
Fig.1.Zinc hydrometallurgy process.

The control performance of the solution purification process directly affects the normal functioning and the economical benefits of zinc hydrometallurgy.In theory,the chemistry of the solution purification process is easy to understand,i.e.,use zinc dust to replace the impurities under appropriate reaction conditions.However,in practice,the economical and stable operation of this process is difficult to achieve,especially in plants with a low automation level and jumbly mineral supplies.Owing to the complex process dynamics and the absence of cheap and reliable online equipment for detection of metallic ions,the operators prefer to handle solution purification process in a conservative manner,i.e.,by using an excessive amount of zinc dust to achieve the required purification performance.Nevertheless,this conservative operation is non-economical as well as not completely rational.Excessive amount of zinc dust may cause an increase in the local pH and deteriorate the reaction conditions,which would in turn lead to failure in purification.

The existence of these problems has attracted a lot of attention of researchers from both the metallurgy community and the control community.To the author’s best knowledge,studies on solution purification processes began in 1871[4].After that,research on solution purification has undergone two stages of rapid development[5].The first stage is driven by studies on the mechanism of the solution purification process.The reaction type,reaction step,and the best con figuration of reaction conditions have been extensively investigated in this stage(see e.g.,[2],[6]and references therein).The second stage is promoted by the application of control theories and technologies to the solution purification process.The stability,observation,and regulation problems of solution purification process have been studied in this stage(see e.g.,[5],[7]-[10]and references therein).However,due to the gap between different disciplines.The mechanism study is not totally oriented to control,while the controller design is usually based on an abstract continuous stirred tank reactor(CSTR)model rather than a practical solution purification process.

The authors’recent work on the modeling,optimization,and control of the solution purification process bridges the gap between the hydrometallurgical purification mechanism and process control technology.It is based on an in depth analysis of the mechanism characteristic and technology characteristic of the solution purification process,and is exactly aimed at addressing the aforementioned difficulties.The oxidation reduction potential(ORP),which can be measured online and reflects the reaction rate of solution purification process,is extensively utilized in this research.In view of its significance and advantage,in this work,the modeling,online determination,optimization,and control of the solution purification process are all centered around the ORP.

The rest of the paper proceeds as follows.A detailed introduction of the solution purification process and an analysis of its control problem are given in Section II.The online determination problem of impurity ions is studied in Section III.In Section IV,a steady-state multiple reactors gradient optimization,unsteady-state operational-pattern adjustment strategy,and an adaptive additive dosage strategy based on online process evaluation are proposed.After the presentation of an industrial experiment in Section V,the paper is concluded in Section VI.

II.PROCESS DESCRIPTION AND PROBLEM ANALYSIS

Zinc ores contain more than one type of associated metal,e.g.,Iron(Fe),copper(Cu),cobalt(Co),and cadmium(Cd).These impurities possess different physical and chemical properties.Consequently,the solution purification process is composed of multiple steps,i.e.,copper removal[11],cobalt removal[12],and cadmium removal,with each step designed to remove a particular type of impurity under specific reaction conditions(Fig.2).Iron removal[13],which is located in the leaching process to remove iron by forming goethite,holds a similar function.

Fig.2. Solution purification process.

Although these impurity removal processes adopt different techniques and reaction conditions,they do share some common features.As shown in Fig.3,impurity removal is conducted in consecutive continuous stirred reactors,and zinc dust is used as an additive to replace the target impurity under the assistance of a catalyst.Without loss of generality,the replacement reaction can be expressed as:

where Zn is zinc dust,Im is the impurity metal,a,b,m,n∈N+,andbm=an[14].After retention in consecutive reactors,the solution flows into the thickener,where the liquid-solid separation takes place.The over flow of the thickener is filtered and delivered to the subsequent process,while the under flow that contains the crystal nucleus beneficial to impurity removal is recycled to promote purification.The spent acid and steam are also supplied to maintain suitable pH and temperature of the solution.

The economical operation of an impurity removal process involves adjusting the zinc dust dosage and reaction conditions such that:

1)The effluent impurity ion concentration of the last reactor is lower than a prede fined value;

2)Zinc dust consumption is as low as possible;

3)Impurity removal process is as stable as possible.

However,the achievement of economical operation encounters the following difficulties.

A.Complex Reaction Mechanism

The chemical reactions conducted in the solution purification process are not unique.Besides the main reaction(1),there exist other simultaneously occurring reactions that interact with the main reaction in a cooperative or competitive manner.In addition,a large number of process parameters can affect the main reaction,e.g.,particle size of zinc dust,type of catalyst,reaction temperature,solution pH,etc.Thus,the reaction mechanism of solution purification is complex and hard to describe.

B.Delayed Detection

Concentrations of the impurities in the pregnant leaching solution and the effluent solution of each reactor are key parameters in the determination of zinc dust dosage and reaction conditions.However,online equipment for detecting metallic ions are usually expensive,difficult to maintain in hostile production environments,and not very reliable[15],[16].As a compromise,impurity ion concentrations are usually determined periodically(the sampling period is counted by hours)by a time consuming artificial chemical assay.Therefore,human operators cannot get access to the real-time information of impurity ion concentrations.

Fig.3. Impurity removal process.

C.Multiple Running Statuses

In plants with jumbly mineral supplies,the physical and chemical properties of zinc ores vary randomly.The operations in the preceding steps of solution purification may not always lead to satisfying results.As a consequence,the inlet conditions,which include the flow rate,concentrations,and types of the impurities in the pregnant leaching solution,are time varying[5].On the other hand,with limited knowledge and information,the operators cannot always adjust the control variables in accordance with the variation of the inlet conditions.Thus,as a synthesized outcome of the interlaced variations of inlet conditions,reaction conditions,and zinc dust dosages,the solution purification process exhibits various kinds of running statuses.Further,under different running statuses,the solution purification process has different dynamics and operation targets.Thus,inflexible control strategies are not suitable in this circumstance.

The above mentioned difficulties prevent the operators from making optimal decisions.In order to achieve the desired purification performance,an excessive amount of zinc dust is usually added.However,the relationship between zinc dust dosage and purification performance is not positively correlated.Redundant zinc dust would react with hydrogen ions.This could increase the local pH,resulting in the formation of basic zinc sulfate,which could stick to the surface of zinc dust and hinder impurity removal.Thus,this conservative operation manner is not completely rational.A control method that incorporates the online determination of impurity ion concentration and adapts to the variation of running status is therefore required.

III.ONLINE DETERMINATION OF IMPURITY ION CONCENTRATION

Determination of metal ion concentration is usually based on the specificity of a metal’s physical properties.For example,spectrophotometry,polarography,and inductively coupled plasma(ICP)analysis utilize the difference of metals in the absorbance wave,polarographic wave,and electromagnetic property,respectively[2].From the perspective of electro-chemistry,the reaction to remove the impurity is essentially an electrode reaction composed of many parallel electrode reactions.The unique shared characteristic of these parallel electrode reactions is the ORP,which determines the rate of electrode reaction by affecting the electron transfer rate between the oxidant and reductant[17].The advantage of ORP is that it can be monitored online by an ORP meter,which is a low-cost and industrially feasible device[16].This section studies the problem of online determination of impurity ion concentration based on ORP.By a comprehensive mechanism study[2],the analytic relationship between ORP and reaction rate is first revealed.Then,the nominal kinetic model of the solution purification process is developed based on the findings.A multiple time-scales model compensation approach is devised to decrease the model-plant mismatch.

A.Nominal Kinetic Model of Impurity Removal Process

The relationship between ORP and reaction rate has been studied previously in[2].It is found that in a certain range,a more negative ORP represents a faster reaction rate and vice versa

wherekis the reaction rate constant,eorpis ORP of the solution,AFis the frequency factor,Eeis the standard activation energy,Fis the Faraday constant,Ris the ideal gas constant,Tis the reaction temperature,eeqis the equilibrium potential,andγis the influence factor of electrode potential variation to cathode activation energy.

Consider that an impurity removal process containsN(N∈N+)reactors,and assume that the fluid in each reactor is perfectly mixed,i.e.,the concentrations,temperature,and reaction rate are the same everywhere in the entire reactor.Then,according to the mass balance principle,the nominal kinetic model of impurity removal process is

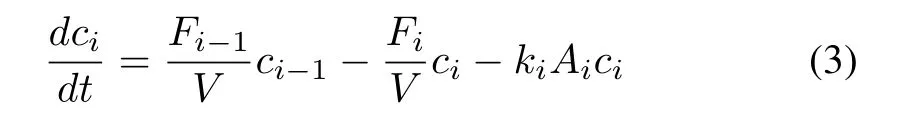
wherei=1,2,...,N,Vis the volume of the reactor;ci-1andciare the influent and effluent impurity ion concentrations of theith reactor,respectively;kiandAiare the reaction rate constant and reaction surface area in unit volume of theith reactor,respectively;andFi-1andFiare the influent and effluent flow rate of theith reactor,respectively.In particular,F0=Fin+Fu,whereFinis the flow rate of the input leaching solution from previous stage,andFuis the flow rate of the recycled under flow.The unknown parametersθ=[AF,Ee,γ,eeq,A]in the nominal model can be identified from the historical production data.

Fig.4.Kinetic model test result of reactor 1-4.

B.Multiple Time-scales Model Compensation

Owing to the diversity and variability of the running status,application of the nominal kinetic model with fixed parameters may possibly generate a large bias in the online determination of impurity ion concentration.To decrease the model-plant mismatch,a model compensation is required.In the authors’work,various model compensation methods were proposed,e.g.,1)sub kinetic models for each running status[11]:Impurity removal exhibits various running status.Under different running status,kinetic model parameters take different values.Build sub kinetic models is to divide industrial data into several condition classes according to the performance of the kinetic model,and identify kinetic model parameters for each running status,respectively;2)data-driven compensation[2]:Impurity removal is a complex multi-phase reaction influenced by numerous factors,the complex influence mechanism of various factors cannot be completely described by the kinetic model;second,the theorem and principle adopted in deducing the kinetic model are based on assumptions and were obtained under specific conditions,while in practical processes,the mechanisms may behave differently.Application of DCS(distributed control system)and FCS(fieldbus control system)in metallurgy plants enables collection of daily operation data which contains abundant information about the nature of the process.Data-driven compensation use regression methods to learn from the data,i.e.,train a model using the data which could reconstruct the relationship between important process variables and impurity ion concentration.Fig.4,Fig.5 and Table I illustrate the application of data-driven compensation to a cobalt removal process.The maximum relative error and average relative error is obviously reduced which indicates the effectiveness of integration;3)model updating[13],[16]:In the industrial field,many factors lead to the perturbation or variation of process dynamics,such as fluctuations in the working conditions,environmental disturbances,and so on.The prediction precision of the model probably deteriorates with a change in the production condition or time.It is necessary to correct the kinetic model or data-driven compensation model on-line to improve the adaptability.Model updating is to re-identify the kinetic model parameters or retain the data-driven compensation model periodically or when the model error is lager than a predefined limit.

TABLE IPERFORMANCE TEST OF INTEGRATED MODEL(%)

These methods can be further utilized to construct a“multiple time-scales model compensation”framework,which includes small time scale,medium time scale,and large time scale compensations(Fig.6).The framework contains two stages:of fline stage and online stage.The preparation work is done in the offline stage which mainly utilizes the historical data with a relatively wide distribution.The kinetic model parameters of each running status{θ1,θ2,...,θK}(k∈N+is the number of classified running status)are identified.The data-driven compensation model is trained using historical data.In the online stage,the realtime data,which distributes in a relative small space and reveals the realtime situation,are processed to support the compensation decision.The running status is firstly identified using real-time values of process variables,and the corresponding sub kinetic model is selected.The result of the data-driven compensation modelcˆ2is integrated with the output of the nominal kinetic modelcˆ1as a small time

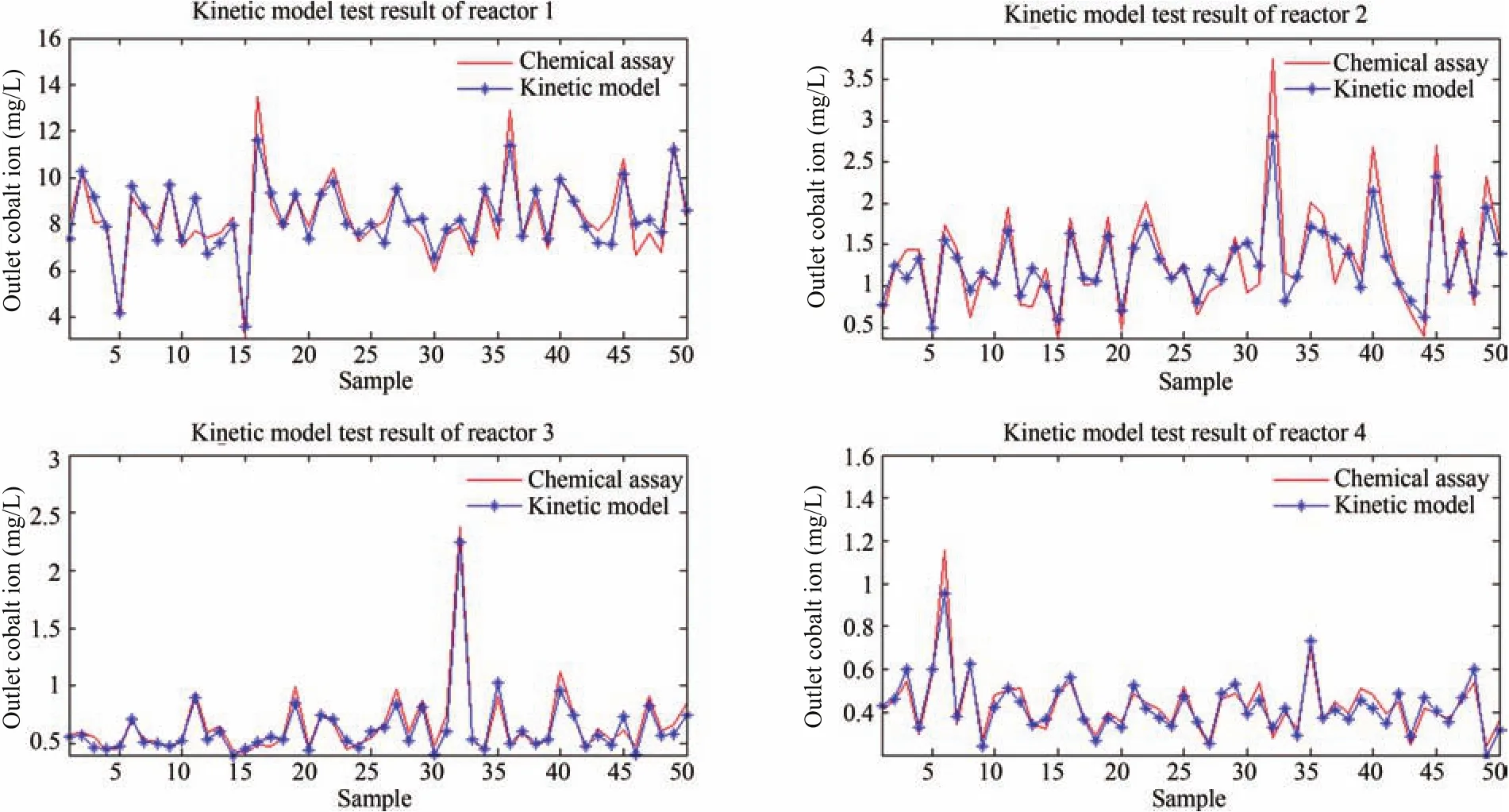
Fig.5.Integrated model test result of reactor 1-4.

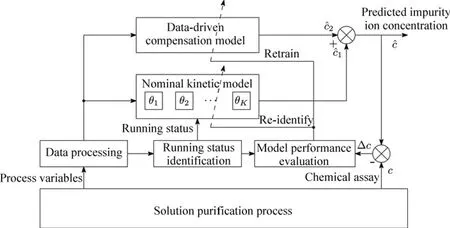
Fig.6. Multiple time-scales model compensation.

scale compensation.The performance of the integrated model is evaluated continuously based on its mismatch with the actual plant.The data-driven compensation model is retrained if the relative error is e.g.,between 15%and 20%more than twice,or retrained weekly to proceed a medium time scale compensation.The parameters of the kinetic models are re-identified if the mismatch is e.g.,larger than 20%more than once,or re-identified monthly to make a large time scale compensation.

IV.OPTIMIZATION AND CONTROL OF SOLUTION PURIFICATION PROCESS

For almost every industrial process,the realization of control objectives relies on a subtly designed control strategy,which can only be obtained based on an indepth understanding of process characteristics[18].The solution purification process possesses multiple running statuses.Under different running statuses,the process dynamics and operation targets are different.When the solution purification process is under the steady-state,minimizing production cost is the main concern.When the solution purification process is under the unsteady-state,recovering to a steady-state is much more important than saving of zinc dust.Thus,the steady-state multiple reactors gradient optimization,unsteady-state operational-pattern adjustment strategy is proposed for the solution purification process.

A.Steady-state Multiple Reactors Gradient Optimization

Zinc dust dosage is of great importance to the production cost and purification performance.An excessive amount of zinc dust is a waste of costly material,while an insufficient amount fails to remove the impurity adequately.The steady-state optimization aims to find the best combination of zinc dust dosages of each reactor in order to optimize the total zinc dust consumption.

Consider a single reactor:at any moment,its mass balance can be expressed as

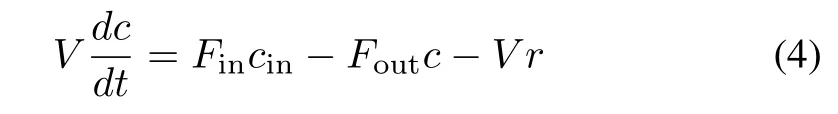
wherecinandcrepresent the in fluent and effluent cobalt ion concentration,respectively;FinandFoutare the in fluent and effluent flow rate;Vis the volume of the reactor;ris the reaction rate

Theoretically,amol zinc dust can replacebmol impurity ion(see reaction(1)),and the zinc dust dosage raterZnequals to

whereMZnandMImare the atomic weight of zinc and the impurity,respectively.However,the reaction between the impurity ions and zinc dust is affected by numerous factors,such as pH and the viscosity of solution.For example,if the pH is too high,it is liable to form basic zinc sulfate on the surface of the zinc dust,which would reduce the activity of the zinc dust.Thus,in practice,zinc dust cannot completely participate in impurity removal.The required zinc dust dosage rate depends on its utilization efficiency in removing the impurity[5],[19].If we denoteµas the zinc dust utilization factor(ZDUF)or,more generally,the additive utilization efficiency(AUE),then the required dosage rate of zinc dustis

Thus,the total zinc dust dosage rate of an impurity removal process that containsN(N∈N+)reactors is

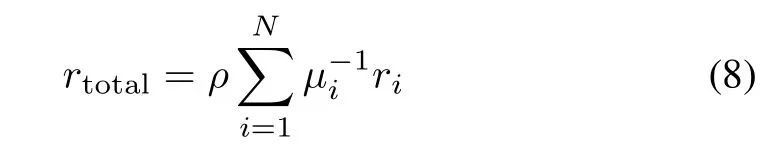
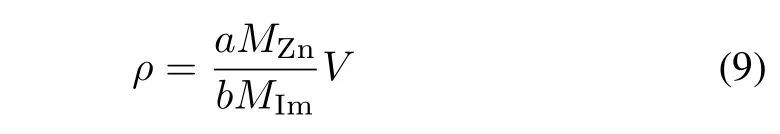
in whichµiandrirepresent the zinc dust utilization efficiency and the reaction rate of theith reactor,respectively.

Thus,the problem of zinc dust dosage optimization can be formulated as follows:

Problem 1:

wheret0andtfare the beginning and end of the optimization range,respectively,Φ={k1,k2,...,kN,A1,A2,...,AN}.Problem 1 indicates that,for an impurity removal process,zinc dust optimization can be achieved by optimizing reaction rate{ri},or{ki}and{Ai},which can then be controlled by adjusting the ORP of each reactor and the flux of the under flow.However,Problem 1 is difficult to solve owing to the uncertainty in the process dynamics and the time-varying characteristic of{µi}.

Problem 1 can be simplified if the impurity removal process is under the steady-state,i.e.,and ifc0and{µi}kept constant.In this case,for each reactor

while for the impurity removal process

in which

λiis the impurity removal ratio(IRR)of theith reactor

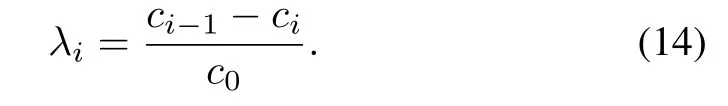
As indicated by(12),assigning impurity removal ratios of each reactor according to their zinc dust utilization efficiencies is an effective way to optimize the zinc dust consumption[5],[20],[21].In addition,the impurity removal ratio is an external indicator of the reaction state inside the reactor.Limiting the impurity removal ratios of each reactor in predefined ranges is beneficial to the stability of the impurity removal process.Then,we can reformulate Problem 1 as:

Problem 2:

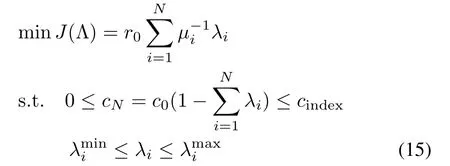
By solving Problem 2,we can obtain the optimal impurity removal ratios of each reactor,which can then be used to calculate the setting values of the effluent impurity ion concentrations.In this sense,solving of Problem 2 can be regarded as a presetting of the steady-state effluent impurity ion concentrations of each reactor in consideration of the current reaction status,or in other words,to find a best decline gradient of the impurity ion concentration along the reactors(Fig.7).However,the impurity removal process cannot always stay at steady-state.c0,{Fi},and{µi}vary with inlet and reaction conditions.Therefore,Problem 2 needs to be solved periodically online.Selection of the optimization period is related to the time-varying characteristic of the target process.Besides the selection of optimization period,estimation of AUE is another important issue.There exist various kinds of methods to estimate the value of AUE[19],such as regression method,Box-Jenkins method,etc.In this work,radial basis function neural network(RBFNN)[22],which has been applied successfully in many engineering problems[23]-[25],is selected to estimate AUE.The RBFNN consists of three layers:input layer,hidden layer and output layer.ORP,dosage of zinc dust and arsenic trioxide, flux of zinc sulfate solution,inlet concentration of impurity ions,which are related to the variables in calculation formula of AUE,are selected as input of RBFNN;the hidden layer contains 15 nodes;the output is AUE.The AUE estimation result of a cobalt removal process with 4 reactors is shown in Fig.8 and Table II.When the presetting values are obtained,the optimal zinc dust dosages or ORPs of each reactor need to be determined in order to force the actual effluent impurity ion concentrations of each reactor to track their optimal setting values(Fig.9).Thus,a complete control scheme of the solution purification process should include two layers(Fig.10).The upper layer,which works on a slow time scale,solving the approximated economical optimization problem.The lower layer,which works on a fast time scale,involving the use of a controller to derive the optimal zinc dust dosages or ORPs of each reactor.

Fig.7. Gradient optimization along reactors.Tirefers to the average time for a unit volume of solution to flow from the inlet of the first reactor to the outlet of reactor i(i=1,2,...,N).

Fig.8.AUE estimation of reactors 1-4.

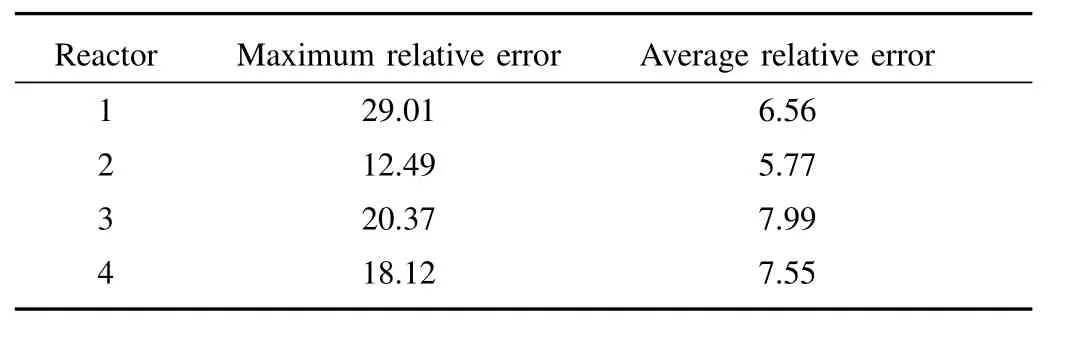
TABLE IIPERFORMANCE TEST OF AUE ESTIMATION MODEL(%)

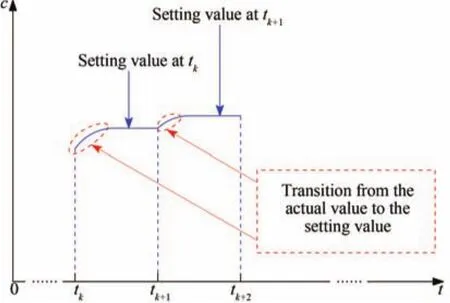
Fig.9. Transition from actual effluent impurity ion concentration to the setting value.

B.Unsteady-state Operational-pattern Adjustment

The recovery from unsteady-state to steady-state is more complex than steady-state optimization.Only adjusting the zinc dust dosages of each reactor is not sufficient for the recovery.A collaborative adjustment between the zinc dust dosages and reaction conditions is needed.Such a collaborative adjustment is generally difficult owing to the complex process dynamics and strong couplings between the operation parameters.However,the adjustment rules can be discovered from the massive amount of daily routine process operating data[26].

Without loss of generality,the operation and its output under certain working conditions can be formulated as an operational-pattern[27]

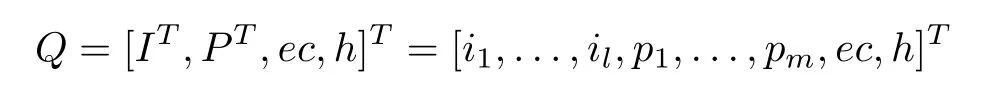
whereQis the operational-pattern,I∈Rl×1are the working conditions,P∈Rm×1are the operation parameters,ecis the production cost,andhis the time when the operational-pattern is generated.

Successful operations can be stored as operational-patterns and reused in similar scenes.As shown in Fig.11,a collaborative optimization frame for operating parameters based on fuzzy operational-pattern is proposed for the unsteady-state adjustment.The initial operational-pattern base is first constructed by applying expert experience and analyzing operation data.Optimization of operation parameters is done according to the following steps:

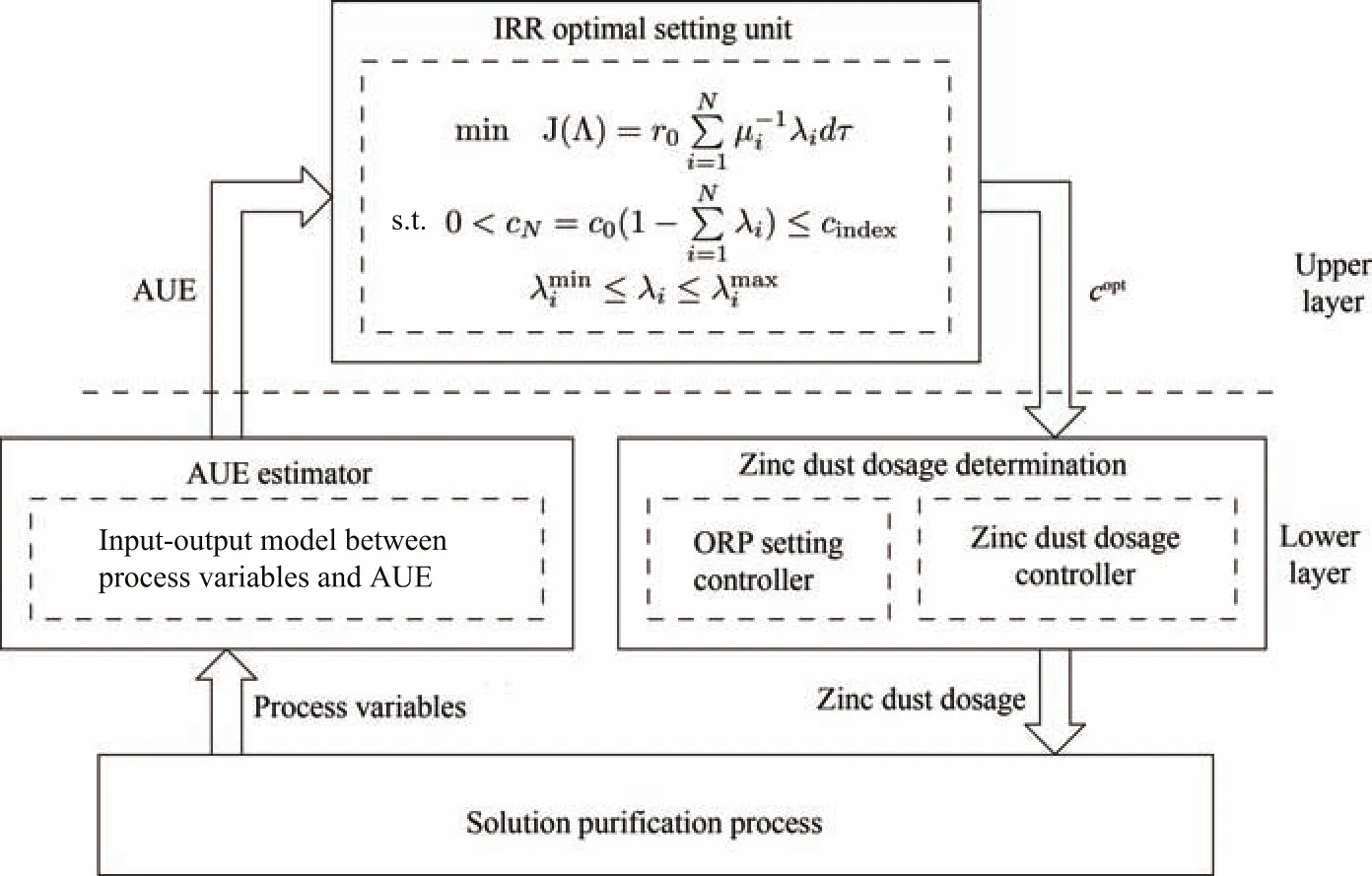
Fig.10. Two layer control scheme.

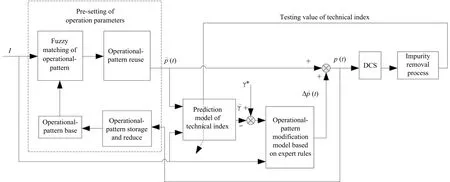
Fig.11.Collaborative optimization of operation parameters based on operational-pattern.

1)Operational-patternFuzzyMatching:Optimization based on an operational-pattern is essentially similar to experiential reasoning,which is fuzzy and heuristic.Thus,before selection of similar operational-patterns,the current working conditionsIare fuzzified.It is first mapped to a standardized domainU.Its membership to a fuzzy subset˜Ais calculated using a trigonometric membership function:

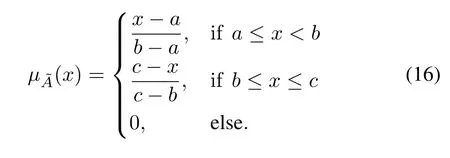
In this application,the fuzzy set contains seven linguistic variables,i.e.,1=NB(negative big),=NM(negative medium),=NS(negative small),=ZO(zero),=PS(positive small),=PM(positive medium),and=PB(positive big).

After fuzzification,previous successful operational-patterns in the operational-pattern base are selected according to their similarity to the current working conditions;only the operational-patterns whose similarity is greater than a threshold are selected and reused

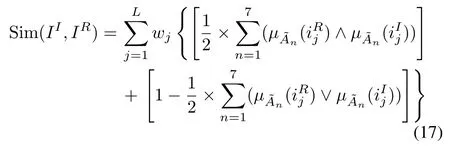
whereIIandIRare the working conditions of the current input case and the retrieved case,respectively.wjis the weight of thejth operational parameter.

2)Operational-pattern Reuse:The selected operational-patterns cannot be reused directly.Because of the highly noisy,strongly acidic,and highly corrosive production environment,the optimal operation parameters under the same working conditions are time-varying.Thus,the longer the operational-pattern is generated,the lower its reference significance and the smaller weight it should be assigned.Similarly,the selected operational-pattern with a higher zinc dust consumption should be assigned a smaller weight to reduce the production cost.IfRoperational-patterns are selected,then the weight of therth operational-patternβris:

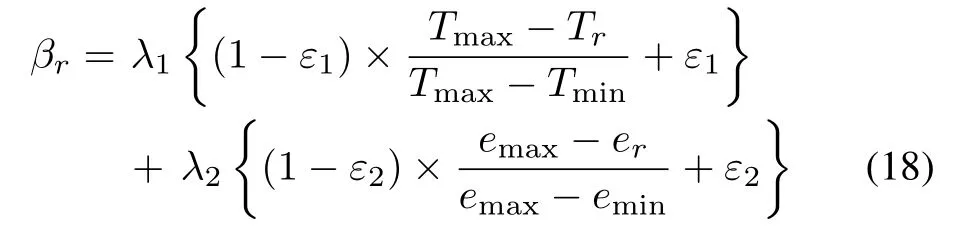
whereTmaxandTminare the times when the oldest and newest operational-patterns are generated,emaxandeminare the highest and lowest zinc dust consumption of the selected operational-patterns,ε1,ε2∈[0,1],λ1,λ2∈[0,1],andλ1+λ2=1.

If the operation parameters in the selected operational-patterns arePr=(pr,1,pr,2,...,pr,m),then based on the evaluation of the reference significance,the derived operation parametersP=(p1,p2,...,pm)are

wheres=1,2,...,m.

3)Operation Parameters Modification:Through Steps 1)and 2),the pre-setting values of the operation parameters are obtained.Before the pre-determined operation parameters are physically applied to the actual system,they must be evaluated and modified to guarantee that the outlet impurity ion concentration is no larger than a prede fined value.The modification is made based on expert rules.

4)Operational-pattern Storage and Reduction:The size of the operational-pattern base will increase as time progresses.To limit the size of the operational-pattern base,useless operational-patterns should be discarded.

The steady-state multiple reactors gradient optimization,unsteady-state operational-pattern adjustment control strategy has been applied to iron removal[21]and cobalt removal process[12].By virtue of the online measurable property of ORP,as an alternative,an adaptive zinc dust dosage strategy based on online process evaluation has been proposed and applied in the control of copper removal process[16].

C.Adaptive Zinc Dust Dosage Strategy Based on Online Process Evaluation

Besides the steady-state multiple reactors gradient optimization,unsteady-state operational-pattern adjustment strategy,adjusting the zinc dust dosages of each reactor adaptively according to the reaction state is a rational way to handle the impurity removal process,especially the impurity removal process with frequent fluctuations.In this sense,online evaluation of the reaction state is necessary.The solution purification process involves a variety of oxidation-reduction reactions or electrode reactions.Thus,ORP,which can be measured online continuously and reflects the extent of oxidation-reduction reaction,provides insight into the state of the reaction system that other process parameters cannot reveal.The value of ORP presents the current state of the removal process,while its trend indicates the underlying future state under the current operation[16].

Similar with optimization based on operational-pattern,the relationship among ORP,trend of ORP,and process state is uncertain and fuzzy.Therefore,fuzzy logic is introduced to evaluate the state of the impurity removal process.The ORP and its trends are first classified into several fuzzy sets with several fuzzy membership functions.Then,according to the fuzzified ORP and its trend,the reaction state is graded by applying a set of fuzzy inference rules.Finally,the zinc dust dosages are adjusted adaptively based on the evaluated grade.The evaluation and adjustment procedure mainly consists of the following four stages:

1)Real-time ORP Trend Extraction:Assume that in the regression window with sizeW,the evolution of ORP is approximated by

wherek0is the initial time step,(k)is the approximated value at thekth time step,azandbzare parameters to be identified by minimizingS

wherex(ki)is the real value of ORP at thekith time step.The fitted parameterazis considered as the ORP trend.The extraction of the ORP trend is conducted in a receding horizon manner.If new data is generated,then the values ofazandbzare updated.

2)Fuzzi fication:Once the input variables including ORP and its trend are prepared,these quantitative variables are transformed into linguistic variables.Three types of membership functions are applied:the generalized bell membership function(22),Z-shaped,and S-shaped membership functions((23)and(24)):

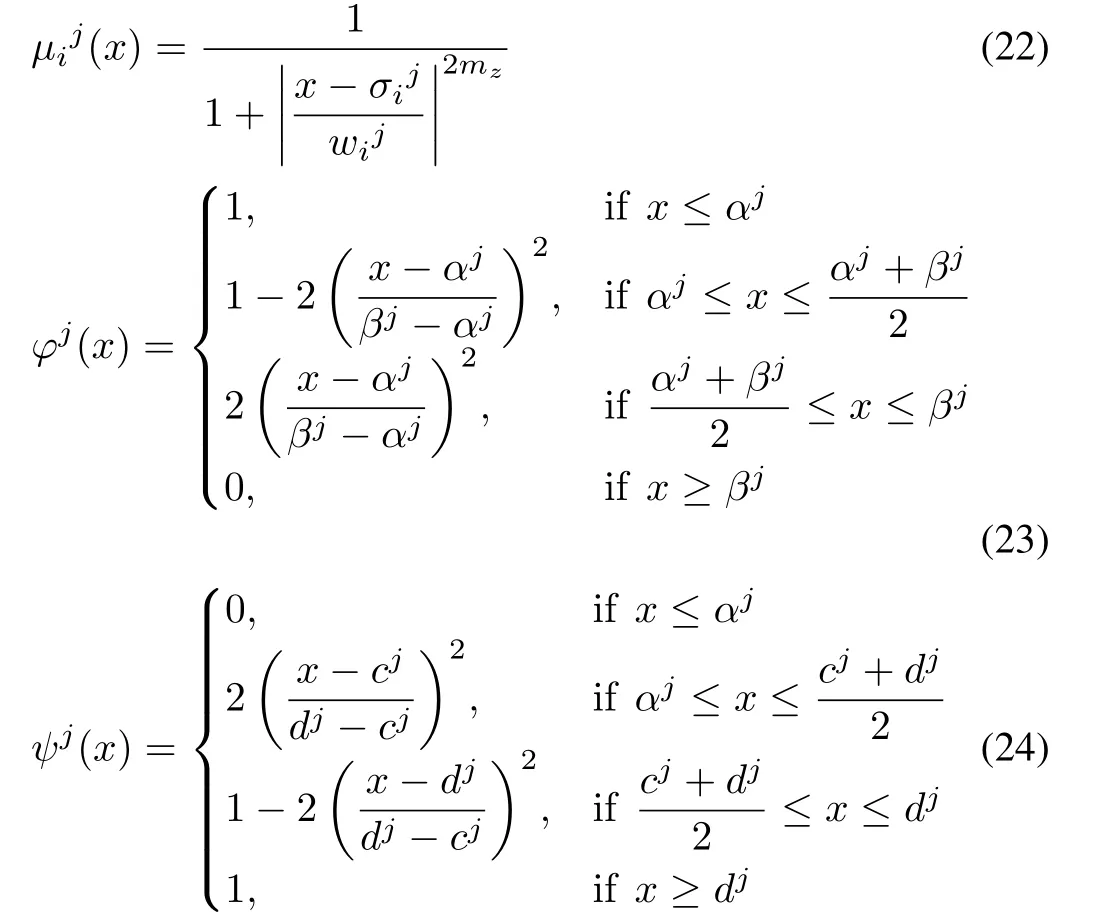
The parameters of these membership functions are obtained on the basis of the kinetic model and the requirement of the outlet impurity ion concentration[16].

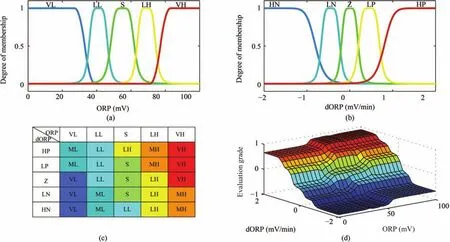
Fig.12.Fuzzy logic evaluation of an impurity removal process based on ORP for:(a)and(b)the memberships of ORP and its trend,respectively;(c)the fuzzy interference rules;and(d)the relationships among the evaluation grade,ORP,and its trend([16],pp.298).

To make the evaluation more accessible and intuitive,the fuzzy sets are labeled by the fuzzy languages in accordance with their corresponding physical meanings in the removal process.Specifically,the ORP reflects the changes in impurity ion concentration in the reactors.It increases with increasing impurity ion concentration and vice versa.When the impurity ion concentration is located at the center of the production limits,the ORP is in a stable situation,which is labeled as S.The lower the concentration,the lower the ORP.Thus,when the ORP is in a lower range,the fuzzified ORP can be labeled as little low(LL)or very low(VL).Similarly,ORP in a higher range can be classified as little high(LH)and very high(VH).The trend of the ORP reveals the underlying variation of the future state of the ORP.A sharp trend can cause the ORP to return to a stable situation from an unstable situation in minutes,or cause the ORP to deviate from a stable situation in a few seconds.Thus,the parameters in the memberships of the ORP trend are de fined according to its possible influence on the ORP.De fine an observation intervalτ(min).If the fluctuation of the ORP is negligible duringτminutes,the trend of the ORP is considered as zero(Z).If the ORP might skip or drop from its current value to a higher or lower value duringτminutes,its trend is considered as low positive(LP)or low negative(LN),respectively.If the ORP skips or drops from the stable situation to the highest or lowest value,its trend is labeled as high positive(HP)or high negative(HN),respectively.The shapes of the memberships are shown in Figs.12(a)and(b).

3)Fuzzy Inference Based Evaluation and Grading:In Stage 3),a set of rules is applied to the fuzzy sets obtained in Stage 2)for evaluating the impurity removal process.When the ORP is in an acceptable situation without fluctuation,and its outlook is also acceptable,the impurity removal process is definitely in a stable condition.When the ORP is acceptable but with a sharp trend that causes a cloudy outlook,the process is not stable as expected.In contrast,when the ORP is beyond the limits but with a good trend that could cause it to return to the acceptable state,the process situation is not as bad as it seems to be.According to this idea,the specific evaluation standard,presented as reference rules,is illustrated in Fig.12(c).The evaluation linguistic variables are obtained by the Max–Prod operator following Larsen’s fuzzy inference method.The linguistic variables are then converted into a single numerical output value.The centroid defuzzification method is applied where the crisp value of the output variable is computed by finding the center of gravity of the membership function for the fuzzy value.The value of the output is given by the algebraic expression:

where the non-fuzzy valuey∗represents the evaluation grade of the impurity removal process.A more positive grade means a situation with a higher concentration and vice versa;an evaluation grade closer to zero indicates a more stable process condition.Fig.12(d)shows the evaluation grade surface of the process,which displays the relationship between two inputs(ORP and its trend)and the response output(evaluation grade).

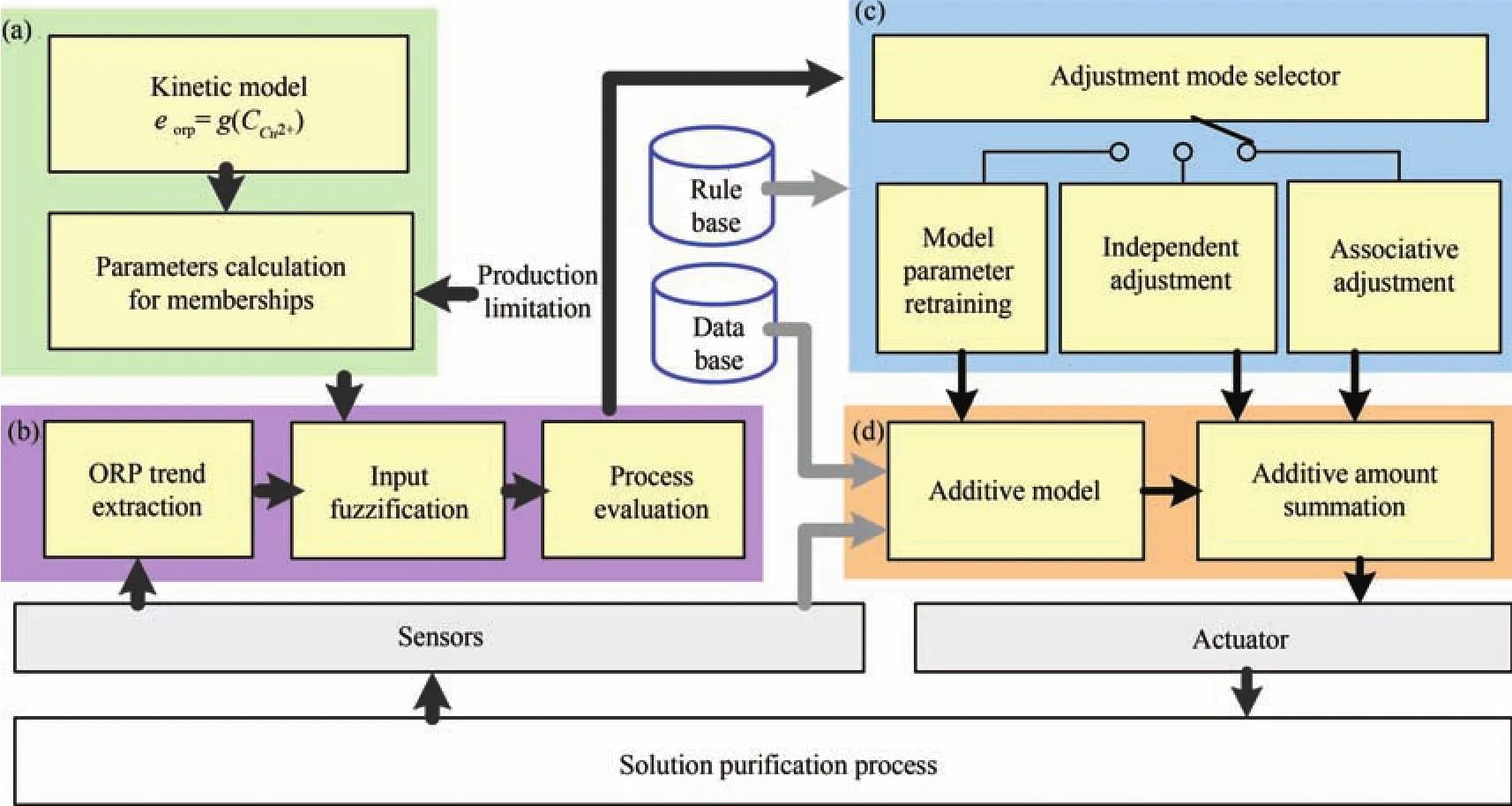
Fig.13. Evaluation and control system for an impurity removal process:(a)the evaluation range estimation unit;(b)the process evaluation unit;(c)the additive adjustment unit;and(d)the additive control unit([16],pp.299).

4)Adaptive Zinc Dust Dosage Adjustment:Reactors in impurity removal process undertake different tasks.Most of the impurity ions are removed in the first one or two reactors,while the last reactor is used for fine tuning.The operators can only adjust the zinc dust dosages of the first one or two reactors,or adjust all the reactors in an associated manner.The adjustment mode can be determined based on the evaluation result.As shown in Fig.13,the system consists of an evaluation range estimation unit,a process evaluation unit,an additive adjustment unit,and an additive control unit.The evaluation range estimation unit translates the production limitation of the outlet concentration to an ORP range based on the proposed kinetic model.The process evaluation unit then assesses the process condition using ORP and its trend.By analyzing the evaluation results,the adjustment mode selector produces an adjustment mode signal.Then,the corresponding adjustment mode is activated by the signal.If the model retraining mode,which could also be chosen by determining whether pH and temperature exceed set ranges,is chosen,a new set of parameters would be trained according to the recent industrial data from the database for the existing additive model.When the independent adjustment mode is chosen,the adjustment amount of zinc powder added in the second reactor would be calculated based on the expert system.Similarly,if the associative adjustment mode is selected,zinc amounts added in all the reactors would be adjusted.In the additive control unit,the additive model sets the major amounts for the process,and the final amount of zinc powder added in each reactor is set by summing the major and adjustment amounts.The readers are referred to[5],[16],and[21]for more details.

V.INDUSTRIAL EXPERIMENT RESULTS

To demonstrate the feasibility of the proposed method,a solution purification process in an actual zinc hydrometallurgy plant is considered.The proposed control strategy is coded into the control system software using Visual C++6.0.The control system software are installed for the iron removal process,copper removal process,and cobalt removal process.The main interfaces of the control system software are shown in Figs.14-16.

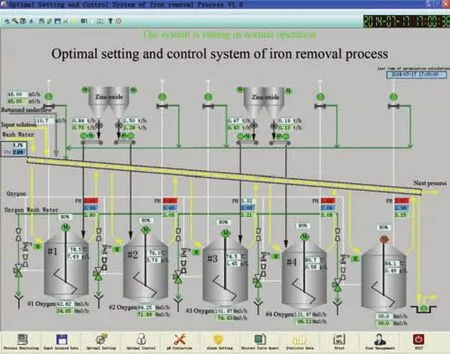
Fig.14.Monitoring and control system of iron removal process.

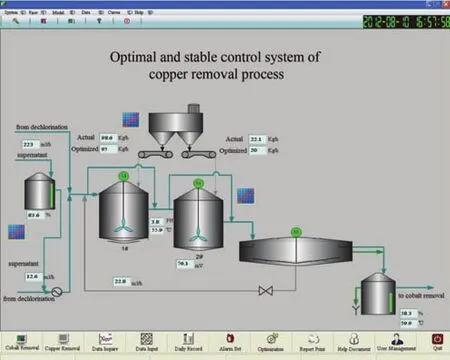
Fig.15.Monitoring and control system of copper removal process.

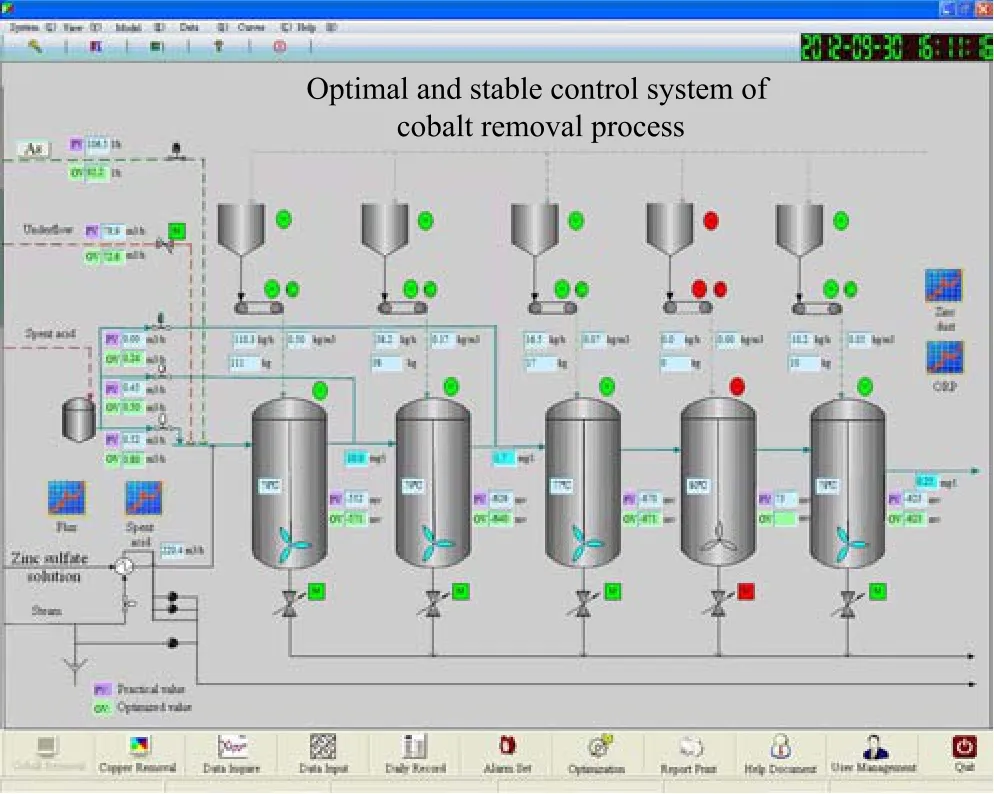
Fig.16.Monitoring and control system of cobalt removal process.

The control system software are linked with the distributed control system(DCS)through an intranet.The real-time value of process variables are transferred from the DCS to the control system software by using an OPC client.The control system software runs the control strategy and gives the setting values of control variables that are finally sent to the DCS.

The effectiveness of the proposed method has been verified by industrial experiment results.The improvements are expressed from the following aspects:

1)Decreased Zinc Dust Consumption:The industrial experiment conducted on Sep.19,2012 to Sep.25,2012 for a cobalt removal process is taken as an example[12].The daily average zinc dust consumption in the industry experiment is 0.6518kg/m3.It is lower than the average zinc dust consumption in the remaining days of Sep.2012,which is 0.7652kg/m3.However,the daily average outlet impurity ion concentration in the experiment is 0.3792mg/L,which is nearly equal to the average outlet impurity ion concentration of the other days in Sep.2012 and satis fies technical requirement of 0.5mg/L.

2)Increased Stability:The fluctuation in the effluent impurity ion concentration is gradually attenuated from the first reactor to the last reactor[5].This is due to the constraints on the IRRs of each reactor and the use of the two-layer steady-state control structure with its lower layer to handle the uncertainties using ORP or zinc dust dosage controller.

3)More Rational Operation:As shown by Figs.17 and 18,the impurity ion concentration decline gradient has changed,which indicates that more impurity ions are removed in the first two reactors with higher additive utilization efficiency.The daily zinc dust consumption is also very stable.This indicates that no excessive zinc dust is added and no sudden change in zinc dust dosage is made.

VI.CONCLUSION

In the current scenario of resource shortage,applying advanced process control technologies to realize economical and green production has become a global concern,especially in some developing countries with a large process industry.The authors’work provides a cheap yet reliable solution for a typical nonferrous metallurgical process.A steady-state multiple reactors gradient optimization strategy,an unsteady-state operational-pattern adjustment strategy,and a process evaluation strategy based on oxidation-reduction potential are proposed.Industrial experiment results indicate the effectiveness of the proposed approach.In future work,the above research will be further improved.

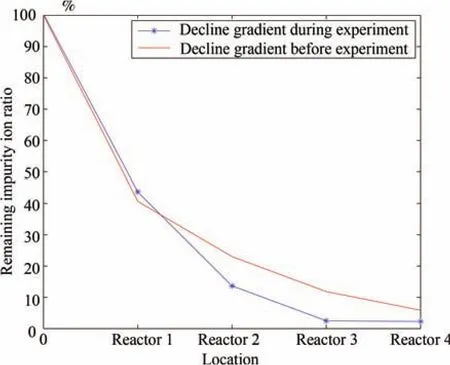
Fig.17.Variation in decline gradient.

Fig.18.Daily average zinc dust consumption.

ACKNOWLEDGMENT

The authors would like to thank Dr.Fuqiang Xiong,Dr.Tiebin Wu,Dr.Bin Zhang and Ph.D.candidate Shijun Deng,Shiwen Xie,Yiting Liang for their contribution to this project.

[1]W.H.Gui and C.H.Yang,Intelligent Modeling Control and Optimization in Complex Non-ferrous Metallurgical Production Process.Beijing,China:Science Press,2010.

[2]B.Sun,W.H.Gui,T.B.Wu,Y.L.Wang,and C.H.Yang,“An integrated prediction model of cobalt ion concentration based on oxidation-reduction potential,”Hydrometallurgy,vol.140,pp.102-110,Nov.2013.

[3]K.Svens,“Outotec atmospheric zinc concentrate direct leaching processpast,present and future,”World Metallurgy-ERZMETALL,vol.63,no.3,pp.136-144,May2010.

[4]O.Bockman and T.Ostvold,“Products formed during cobalt cementation on zinc in zinc sulfate electrolytes,”Hydrometallurgy,vol.54,no.2-3,pp.65-78,Jan.2000.

[5]B.Sun,W.H.Gui,Y.L.Wang,C.H.Yang,and M.F.He,“A gradient optimization scheme for solution purification process,”Control Eng.Pract.,vol.44,pp.89-103,Nov.2015.

[6]B.Krause and R.F.Sandenbergh,“Optimization of cobalt removal from an aqueous sulfate zinc leach solution for zinc electrowinning,”Hydrometallurgy,vol.155,pp.132-140,May2015.

[7]F.Wu,“LMI-based robust model predictive control and its application to an industrial CSTR problem,”J.Process Control,vol.11,no.6,pp.649-659,Dec.2001.

[8]D.L.Yu,T.K.Chang,and D.W.Yu,“A stable self-learning PID control for multivariable time varying systems,”Control Eng.Pract.,vol.15,no.12,pp.1577-1587,Dec.2007.

[9]M.P.Di Ciccio,M.Bottini,P.Pepe,and P.U.Foscolo,“Observer-based nonlinear control law for a continuous stirred tank reactor with recycle,”Chem.Eng.Sci.,vol.66,no.20,pp.4780-4797,Oct.2011.

[10]H.Hoang,F.Couenne,C.Jallut,and Y.Le Gorrec,“Lyapunov-based control of non isothermal continuous stirred tank reactors using irreversible thermodynamics,”J.Process Control,vol.22,no.2,pp.412-422,Feb.2012.

[11]B.Zhang,C.H.Yang,H.Q.Zhu,Y.G.Li,and W.H.Gui,“Kinetic modeling and parameter estimation for competing reactions in copper removal process from zinc sulfate solution,”Ind.Eng.Chem.Res.,vol.52,no.48,pp.17074-17086,Nov.2013.

[12]B.Sun,W.H.Gui,Y.L.Wang,and C.H.Yang,“Intelligent optimal setting control of a cobalt removal process,”J.Process Control,vol.24,no.5,pp.586-599,May2014.

[13]Y.F.Xie,S.W.Xie,X.F.Chen,W.H.Gui,C.H.Yang,and L.Caccetta,“An integrated predictive model with an on-line updating strategy for iron precipitation in zinc hydrometallurgy,”Hydrometallurgy,vol.151,pp.62-72,Jan.2015.

[14]J.A.Se¸dzimir,“Precipitation of metals by metals(cementation)łkinetics,equilibria,”Hydrometallurgy,vol.64,no.3,pp.161-167,Jun.2002.

[15]G.W.Wang,C.H.Yang,H.Q.Zhu,Y.G.Li,X.W.Peng,and W.H.Gui,“State-transition-algorithm-based resolution for overlapping linear sweep voltammetric peaks with high signal ratio,”Chemom.Intell.Lab.Syst.,vol.151,pp.61-70,Feb.2016.

[16]B.Zhang,C.H.Yang,H.Q.Zhu,Y.G.Li,and W.H.Gui,“Evaluation strategy for the control of the copper removal process based on oxidation-reduction potential,”Chem.Eng.J.,vol.284,pp.294-304,Jan.2016.

[17]L.I.Antropov,Theoretical Electrochemistry.Moscow,Russia:Mir Publishers,1977.

[18]B.Sun,C.H.Yang,and W.H.Gui,“A discussion of the control of nonferrous metallurgical processes,”IFAC-PapersOnline,vol.48,no.17,pp.80-85,Aug.2015.

[19]S.I.Kim,K.E.Kim,E.K.Park,S.W.Song,and S.Jung,“Estimation methods for efficiency of additive in removing impurity in hydrometallurgical purification process,”Hydrometallurgy,vol.89,no.3-4,pp.242-252,Dec.2007.

[20]B.Zhang,C.H.Yang,Y.G.Li,X.L.Wang,H.Q.Zhu,and W.H.Gui,“Additive requirement ratio prediction using trend distribution features for hydrometallurgical purification processes,”Control Eng.Pract.,vol.46,pp.10-25,Jan.2016.

[21]S.W.Xie,Y.F.Xie,Y.G.Li,C.H.Yang,and W.H.Gui,“Optimal control of oxidizing rate for iron precipitation process in zinc hydrometallurgy,”Acta Autom.Sinica,vol.41,no.12,pp.2036-2046,Dec.2015.

[22]J.Moody and C.J.Darken,“Fast learning in networks of locally-tuned processing units,”Neural Comput.,vol.1,no.2,pp.281-294,Jun.1989.

[23]S.Seshagiri and H.K.Khalil,“Output feedback control of nonlinear systems using RBF neural networks,”IEEE Trans.Neural Netw.,vol.11,no.1,pp.69-79,Jan.2000.

[24]H.G.Han,J.F.Qiao,and Q.L.Chen,“Model predictive control of dissolved oxygen concentration based on a self-organizing RBF neural network,”Control Eng.Pract.,vol.20,no.4,pp.465-476,Apr.2012.

[25]S.A.Iliyas,M.Elshafei,M.A.Habib,and A.A.Adeniran,“RBF neural network inferential sensor for process emission monitoring,”Control Eng.Pract.,vol.21,no.7,pp.962-970,Jul.2013.

[26]T.B.Wu,C.H.Yang,Y.G.Li,H.Q.Zhu,and W.H.Gui,“Fuzzy operational-pattern based operating parameters collaborative optimization of cobalt removal process with arsenic salt,”Acta Autom.Sinica,vol.40,no.8,pp.1690-1698,Aug.2014.

[27]W.H.Gui,C.H.Yang,Y.G.Li,J.J.He,and L.Z.Yin,“Data-driven operational-pattern optimization for copper fl ash smelting process,”Acta Autom.Sinica,vol.35,no.6,pp.717-724,Jun.2009.