LMI Consensus Condition for Discrete-time Multi-agent Systems
2018-05-02MagdiMahmoudandGulamDastagirKhan
Magdi S.Mahmoud and Gulam Dastagir Khan
I.INTRODUCTION
RECENTLY the problem of distributed consensus in networked multi-agent systems has received significant attention due to its important applications[1].The purpose of the consensus problem is to design a distributed protocol in the presence of limited information communication such that a group of agents achieves some agreement between the states[2].A number of recent papers are devoted to the consensus of multiple LTI systems[3]-[10].However,most of these results[11]-[18],[19]mainly focus on fixed interaction topology,rather than time-varying topology.How the switches of the interaction topology and agent dynamics jointly affect the collective behavior of the multi-agent system?Attempts to understand this issue had been hampered by the lack of suitable analysis tools.The results of Scardoviet al.[20]and Ni and Cheng[21]are mentioned here,because of their contributions dealing with switching topology.
The consensus of multi-agent systems under fixed and switching topology was studied in[21].In[21],the dynamics of each agent and the leader are considered to be linear and in a continuous time domain.The design technique was based on Riccati inequality,algebraic graph theory and Lyapunov inequality.In[22]distributed consensus problem for multiagent systems was considered in the discrete-time domain.The interaction topology among the agents was assumed to be switching and undirected.
By using Schur orthogonal transformation,the closed-loop system was decomposed into two subsystems:one for the leader and the other for a leader-following subsystem.Common Lyapunov function(CLF)approach was employed to investigate the consensus problem.In[23],authors proposed the control of a multi-agent system with state measurement and input disturbances.Distributed dynamic output feedback protocol and linear matrix inequality(LMI)approach were used to address control problem.
The main contributions and primary distinctions of this paper with other works can be given as follows.
1)A more realistic and accurate discrete time model is proposed which is relevant for many practical sampled data systems;
2)A new form for state-feedback control based on the aggregate Laplacian is proposed in this paper;
3)Sufficient conditions of stabilization are established using Lyapunov stability theory.The solution to the decentralized consensus problem is provided in terms of LMI;
4)A comparison is made between the developed algorithm and the existing results.
The organization of this paper is as follows:Firstly,notations,communication graph and preliminaries are introduced in Section II,which are useful throughout this paper.Then in Section III,stability analysis of a multi-agent system is carried out,where in Theorem 1,decentralized consensus problem in multi-agent system is solved by using Schur complement and controller gain matrix is obtained.Later in Section IV,a simulation example is presented along with some comparison to demonstrate the effectiveness of proposed technique.Finally,the conclusion is made.
II.PROBLEM FORMULATION
A.Notations
Throughout this paper,Rnis used to denote the n-dimensional Euclidean space equipped with‖·‖,the standardL2norm on vectors or their induced norms on matrices and R{m×n}is the set of allm×nreal matrices.LetIrbe the unit matrix of orderr.The superscript“T”denotes matrix transposition and “·”denotes the transpose of corresponding elements introduced by symmetry.X>0 means that it is real symmetric and positive de finite;Moreover,X>YmeansX-Y>0 Given a matrixW,letρ(W)denote its spectral radius.For any positive integerN,letIN={1,...,N},diag(W1,...,WN)is a block diagonal matrix with main diagonal block matricesWj,j∈INand the off diagonal blocks are zero matrices.The Kronecker product[24]ofA∈Rp×q:=[aij]andB∈Rm×nis denoted byA⊗Band is apm×qnmatrix de fined by
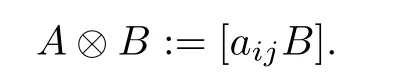
The Kronecker product further facilitates the manipulation of matrices by the following expansion properties
1)(A⊗B)(C⊗D)=AC⊗BD
2)(A⊗B)T=AT⊗BT
3)LetA∈Rr×sandB∈RN×N.
Then(IN⊗A)(B⊗Is)=(B⊗Ir)(IN⊗A)=B⊗A.
B.Communication Graph
Depending on the information flow(unidirectional or bidirectional[24],a graph can be used to express the topology of communication network,either directed or undirected.LetG=(V,E,A)be a weighted directed graph(digraph)of orderN,whereV={v1,...,vN}is the set of nodes andE⊆V×Vis the set of edges.The node indexes belong to a finite index setI={1,2,...,N}.An edge ofGis denoted byeij=(vi,vj),where the first element ofviofvijis referred as tail of the edge and the othervjto be the head.Weighted adjacency matrix is denoted byA=[aij]∈RN×N,where the adjacency elements associated with the edges are positive,that iseij∈E⇔aij>0.A directed graph is said to be undirected if,it satisfies the condition thataij=ajifor anyi,j∈I.The set of neighbors of nodeviis denoted byINi={vj∈V:(vi,vj)∈E}which the index is set of the agents from which theithagent can obtain necessary information.The LaplacianL=[lij]N×Nassociated with the directed graph is defined as

whereINidenotes the number of neighbors of theith agent(the in-degree of agenti).It turns out thatL=Λ-A∈Rn×n,where Λ =[Λij]is a diagonal matrix with Λii=aij.Laplacian matrixLhas the property that,all the row sums ofLare zero and thus an eigenvector ofLassociated with the zero eigenvalue is 1n=[1,1,1,...,1].
Lemma 1:Given integersn,NandA∈Rn×n,R∈RN×N.LetA0=IN⊗AandR0=R⊗In.ThenR0A0=A0R0.
Proof:Using the expansion properties,we obtain
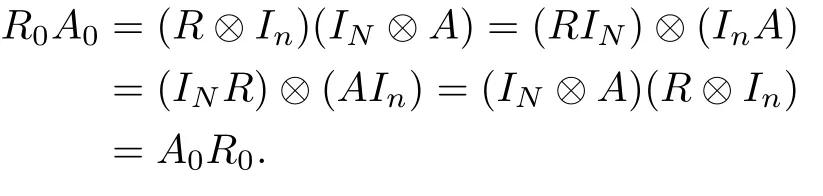
C.Preliminaries
The multi-agent system(MAS)under study is a group ofnagents(1,...,N)with the same dynamics:

wherexi(k)∈Rnis the state of agentiandui(k)∈Rmis the associated control input,through which the interactions or coupling between agentiand other agents are realized.A∈Rn×nandB∈Rn×mare the state and input matrices,whereBis of full column rank.The state information is transmitted among these agents,and the agents together with the transmission channels form a network.The following assumption is used throughout the paper.
Assumption 1:The pair(A,B)is stabilizable[4].
Assumption 2:The interconnection graph of system(1)has a directed spanning tree to guarantee that consensus among agents is possible[9].
Observe that the models of allNagents can be stacked together in the form:

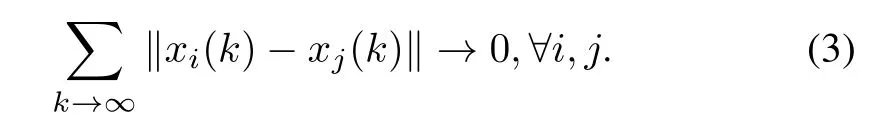
To facilitate further development,we introduce a decentralized control input as
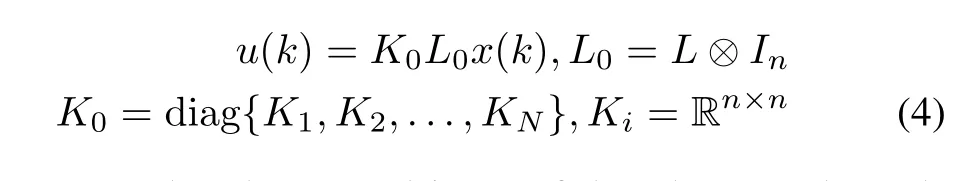
which ensures that the control input of theith agent depends only on states of its neighbor agents and itself.It is important to emphasize that designingK0aims at steering all states to the same vector.
III.STABILIZATION
On combining(2)and(4),the closed-loop system becomes:

Recalling the properties ofL,there exists a vectorxs(k)such that

for someα.It follows with the help of Lemma 1,replacingR0byL0,that
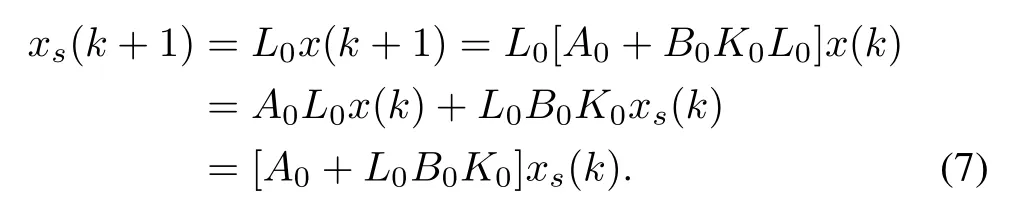
Considering the stabilization of system(7),we invoke Lyapunov stability theory and reach the following result:
Theorem 1:The controller(4)solves the decentralized consensus problem in system(2)if and only if there exists matrices 0<X,0<R,Ysatisfying
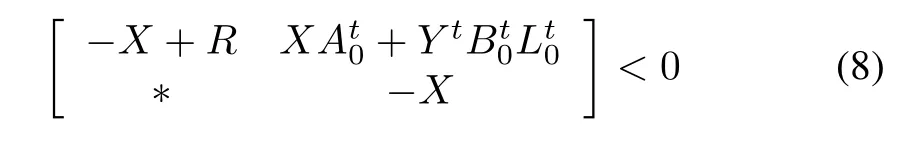
whereK0the gain matrix is given byK0=Y X-1.
Proof:The stability of the closed-loop system(7)implies the existence of matrices 0<P,0<Qsuch that

Invoking the Schur complements,inequality(9)is equivalent to
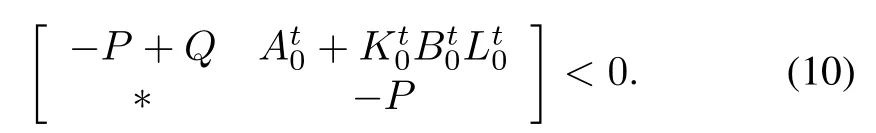
IntroducingX=P-1,R=XQXand applying the congruent transformationT=diag{X,X}to(10),we readily obtain inequality(8)withK0X=Y.
IV.NUMERICAL SIMULATION
In this section,a numerical simulation is presented to illustrate the effectiveness of the developed methodology.Multi-agent system with six agents is considered,where each agent is modeled by following linear dynamics:

It is simple to test that matrix pair(A,B)is stabilizable which satisfies Assumption 1.Consider the communication topology graph as given by Fig.1.Accordingly the Laplacian matrixLis defined as
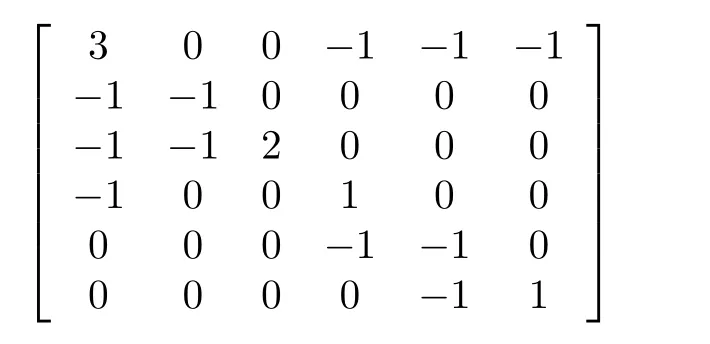
whose non-zero eigenvalues are given by 1,1.33760,+0.5623j,-0.5623j,2,3.2347.For the purpose of simulation,the following initial conditions were selected
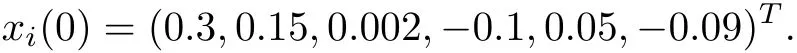
Considering Theorem 1,it turns out that the feasible solution of LMI(8)yields that gain matrix:
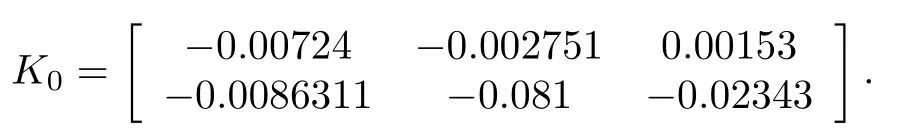
The decentralized control inputu(k)(4)with feedback gain matrices given as above solves the consensus problem for the communication graph in Fig.1.The states of the network(11)with the decentralized control input protocol(4)is depicted in Fig.2.A similar problem has been discussed in[25],[26]where authors investigate average consensus problems in a class of second-order continuous-time multi-agent systems with switching and jointly connected topologies respectively with time-delay,in terms of linear matrix inequalities(LMIs).The simulation results of the state responses obtained in[25],[26]are shown in Figs.3 and 4 respectively.Also in[27],average event triggered discrete consensus control for discrete-time multi-agent systems(MASs)is investigated.Stability criteria were established using Lyapunov matrix inequality.In order to avoid Zeno-behavior certain restriction has been imposed on event condition,which led to conservativeness in the developed algorithm.The simulation results of the state responses obtained in this case are shown in Fig.5.
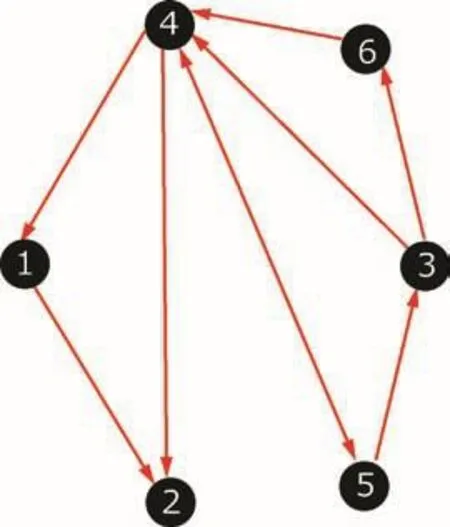
Fig.1:The communication topology.

Fig.2:The state of the network for ith agents where i=1,2,3,...,6 under the decentralized control input.
Several observations can be made from Figs.3-5.Firstly,our proposed control algorithm demonstrates that the consensus condition can be achieved asymptotically with six agents being steered to the same vector.Secondly,the proposed algorithm takes less time to achieve consensus of the multi-agent network.Thirdly,the MAS oscillates with smaller magnitude.Therefore,from the above simulation results,it can be concluded that the proposed technique of decentralized control input can be successfully employed to achieve a consensus of multi-agent network steered to the same vector.
V.CONCLUSIONS
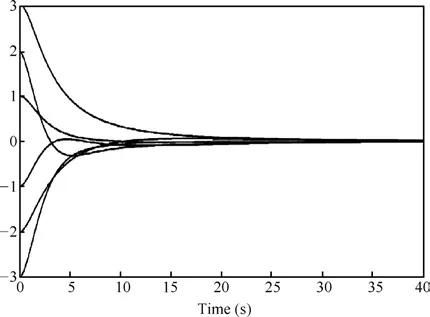
Fig.3:The state of the network for ith agents,using the algorithm developed in[25].
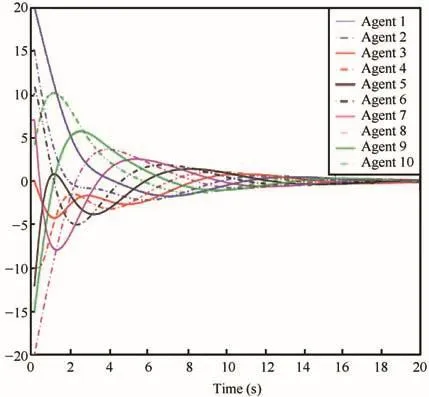
Fig.4:The state of the network for ith agents,using the algorithm developed in[26].
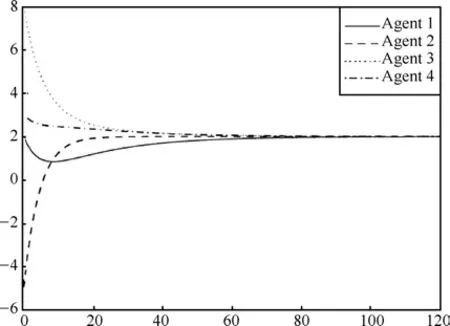
Fig.5:The state of the network for ith agents,using the algorithm developed in[27].
In this paper,a state feedback protocol is designed to solve the consensus problem in discrete-time multi-agent systems in terms of a linear matrix inequality.Feedback gain matrix is obtained by solving the simple LMI.Consensus condition is achieved with six agents being steered to the same vector.In order to show the improved performance of the proposed methodology,the simulation results obtained in this paper are compared with those in[25]-[27].Future work will focus on solving observer based model where the dynamics of the followers are subjected to perturbations as well as leader-following tracking for multi-agent systems with nonlinear dynamics.
[1]R.Olfati-Saber,J.A.Fax,and R.M.Murray,“Consensus and cooperation in networked multi-agent systems,”Proc.IEEE,vol.95,no.1,pp.215-233,Jan.2007.
[2]M.S.Mahmoud,Distributed Control and Filtering for Industrial Systems.UK:IET Press,2012.
[3]W.Ni and D.Z.Cheng,“Leader-following consensus of multi-agent systems under fixed and switching topologies,”Syst.Control Lett.,vol.59,no.3-4,pp.209-217,Mar.2010.
[4]C.R.Wang and H.B.Ji,“Leader-following consensus of multi-agent systems under directed communication topology via distributed adaptive nonlinear protocol,”Syst.Control Lett.,2014,vol.70,pp.23-29,Aug.2014.
[5]M.Defoort,T.Floquet,A.Kokosy,and W.Perruquetti,“Sliding-mode formation control for cooperative autonomous mobile robots,”IEEE Trans.Ind.Electron.,vol.55,no.11,pp.3944-3953,Nov.2008.
[6]D.Cruz,J.McClintock,B.Perteet,O.A.A.Orqueda,Y.Cao,and R.Fierro,“Decentralized cooperative control— A multivehicle platform for research in networked embedded systems,”IEEE Control Syst.,vol.27,no.3,pp.58-78,Jun.2007.
[7]X.H.Wang,V.Yadav,and S.N.Balakrishnan,“Cooperative UAV formation flying with obstacle/collision avoidance,”IEEE Trans.Control Syst.Technol.,vol.15,no.4,pp.672-679,July 2007.
[8]J.M.Chen,X.H.Cao,P.Cheng,Y.Xiao,and Y.X.Sun,“Distributed collaborative control for industrial automation with wireless sensor and actuator networks,”IEEE Trans.Industrial Electron.,vol.57,no.12,pp.4219-4230,Dec.2010.
[9]R.M.Murray,“Recent research in cooperative control of multivehicle systems,”J.Dyn.Syst.,Meas.,Control,vol.129,no.5,pp.571-583,May 2007.
[10]W.Ren and C.Cao,Distributed Coordination of Multi-agent Networks:Emergent Problems,Models,and Issues.London:Springer-Verlag,2011.
[11]X.Li,X.F.Wang,and G.R.Chen,“Pinning a complex dynamical network to its equilibrium,”IEEE Trans.Circuits Syst.I,vol.51,no.10,pp.2074-2087,Oct.2004.
[12]H.W.Zhang,F.L.Lewis,and A.Das,“Optimal design for synchronization of cooperative systems:state feedback,observer and output feedback,”IEEE Trans.Automatic Control,vol.56,no.8,pp.1948-1952,Aug.2011.
[13]R.X.Cui,S.S.Ge,and B.B.Ren,“Synchronized tracking control of multi-agent system with limited information,”inProc.49th IEEE Conference on Decision and Control,Atlanta,GA,2010.pp.5480-5485
[14]Y.G.Hong,G.R.Chen,and L.Bushnell,“Distributed observers design for leader-following control of multi-agent networks,”Automatica,vol.44,no.3,pp.846-850,Mar.2008.
[15]W.Ni and D.Z.Cheng,“Leader-following consensus of multi-agent systems under fixed and switching topologies,”Syst.Control Lett.,vol.59,no.3-4,pp.209-217,Mar.2010.
[16]L.Moreau,“Stability of multiagent systems with time-dependent communication links,”IEEE Trans.Automatic Control,vol.50,no.2,pp.169-182,Feb.2005.
[17]W.Ren,R.W.Beard,and E.M.Atkins,“Information consensus in multivehicle cooperative control,”IEEE Control Syst.Mag.,vol.27,no.2,pp.71-82,Apr.2007.
[18]J.H.Wang and D.Z.Cheng,“Consensus of multi-agent systems with higher order dynamics,”inProc.Chinese Control Conference,Hunan,China,2007.pp.761-765.
[19]W.Ren,R.W.Beard,and E.M.Atkins,“A survey of consensus problems in multi-agent coordination,”inProc.2005 American Control Conference,Portland,OR,pp.1859-1864,2005.
[20]L.Scardovi and R.Sepulchre,“Synchronization in networks of identical linear systems,”Automatica,vol.45,pp.2557-2562,Nov.2009.
[21]W.Ni and D.Z.Cheng,“Leader-following consensus of multi-agent systems under fixed and switching topologies,”Syst.Control Lett.,vol.59,no.3-4,pp.209-217,Mar.2010.
[22]L.X.Gao,C.F.Tong and L.Y.Wang,“H∞dynamic output feedback
consensus control for discrete-time multi-agent systems with switching topology,”Arab.J.Sci.Eng.,vol.39,no.2,pp.1477-1478,Feb.2013.
[23]L.Yang,Y.M.Jia,J.P.Du,and S.Y.Yuan,“Dynamic output feedback control for consensus of multi-agent systems:anH∞approach,”inProc.American Control Conference,St.Louis,MO,2009.pp.4470-4475.
[24]C.Godsil and G.F.Royle,Algebraic Graph Theory.New York:Springer-Verlag,2001.
[25]P.Lin and Y.M.Jia,“Consensus of a class of second-order multi-agent systems with time-delay and jointly-connected topologies,”IEEE Trans.Automatic Control,vol.55,no.3,pp.778-784,Mar.2010.
[26]P.Lin and Y.M.Jia,“Average consensus in networks of multi-agents with both switching topology and coupling time-delay,”Physica A,vol.387,no.1,pp.303-313,Jan.2008.
[27]X.Chen and F.Hao,“Event-triggered average consensus control for discrete-time multi-agent systems,”IET Control Theory Appl.,vol.6,no.16,pp.2493-2498,Nov.2012.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Letter to the Editor Re“Fractional Modeling and SOC Estimation of Lithium-ion Battery”
- Relationship Between Integer Order Systems and Fractional Order Systems and Its Two Applications
- A Novel Approach for Enhancement of Geometric and Contrast Resolution Properties of Low Contrast Images
- An Exploration on Adaptive Iterative Learning Control for a Class of Commensurate High-order Uncertain Nonlinear Fractional Order Systems
- Robust H∞Load Frequency Control of Multi-area Power System With Time Delay:A Sliding Mode Control Approach
- Cyber Attack Protection and Control of Microgrids
