A Model Predictive Scheduling Algorithm in Real-Time Control Systems

Mengya Kang,Chenglin Wen,and Chenxi Wu

I.INTRODUCTION

IN recent years,with the emergence of deferrable loads and development of renewable generation,power grids have attracted a widespread attention.Renewable generation capacity keeps growing at the rate of 10%-60%every year since 2004.By the end of 2014,the consumption of renewable energy accounts for 22.8%of the global energy consumption around the world[1].Power systems would undergo a dramatic transformation over the next few decades,and conventional coal and nuclear generation are being substituted by renewable generation represented by wind and solar generation.However,renewable generation prediction is arduous,for instance,the wind generation prediction would cause a root-mean-square of about 18%of the nameplate capacity looking 24 hours ahead[2].Meanwhile,the industry of deferrable loads represented by electric vehicles(EVs)becomes more and more popular.Deferrable loads refer to the loads whose power consumption can be transferred among different time slots,including EVs and some industrial and commercial loads.Specifically,in a scheduling cycle,the total power consumption is fixed while the power consumption characteristics are flexible,and it’s adjustable to consume power energy at different times.Researches demonstrate that,in 2020,2030 and 2050,the proportion of EVs in total U.S.car will rise to 35%,51%and 62%,respectively[3].The number of deferrable loads has being dramatically increased with the growing popularity of EVs and smart appliances[4].

As a supplement to the power generation scheduling,deferrable loads scheduling can adjust load curves,balance intermittent energy fluctuations and provide auxiliary services,and also be conducive to enrich regulating means of power scheduling operation.Besides,reference[5]uses wind generation as a background,and proposes a flexible scheduling method with security constraints,which can minimize the scheduling cost.A new and efficient hybrid optimization algorithm is proposed in[6]to realize the optimal allocation of the distributed generation system.Besides,a new real-time load modeling method is presented in[7]to minimize the influence of load variation,which is based on a strong tracking filter and a dominant parameter technique to achieve the goal of real-time load modeling.

However,deferrable loads scheduling has been confronted with several new challenges.For example,aggregate load would increase as the result of EVs charging,and it has the potential to amplify peak load or create another new peaks[8].In addition,the challenges could certainly add uncertainties of demand side,reduce the lifespan of power distribution circuits and transformers[9],and cause power loss and voltage change[10].If the control of deferrable loads scheduling is not reasonable enough,even a 10%penetration of EVs could arouse an unexpected variation in voltage pro files[11].Previous researches manifest that these challenges would be mitigated if we take smart charging strategies.The strategy that dispatches EVs to consume power energy in times of load-valley can effectively narrow the differences between peak and valley load, fl at the load curve,and also be beneficial to reduce the operating cost of power companies[12].In addition,the energy stored in EVs can become auxiliary resources to adjust load curves[13],or be a compensation of random fluctuations in renewable generation[14].

Specifically,“smart”charging strategies usually adopt distributed control methods,and studies on load control mainly cover two categories.References[15]-[17]investigate direct load control,where power consumption of each load are determined by a centralized load service entity.However,these strategies require a centralized structure to collect all information of all electric vehicles and optimize over the charging pro files of all electric vehicles,hence incur prohibitive com-munication and computation requirements.Besides,the price-based control is researched in[18]-[20],but does not provide strategies for setting the price.

In addition,considering uncertainties in renewable generation and deferrable loads arrivals,several algorithms for real-time distributed load control have been proposed.References[21]-[23]evaluate algorithms with simulation.References[24]and[25]provide analytic performance guarantee.Reference[26]explores real-time distributed load control with proposing valley filling(VF)algorithm to minimize the variance of aggregate load.

However,the real-time algorithms mentioned above only can be used in deferrable load scheduling when ignoring the constraint of power supply,which can be a ideal case where power supply resource is absolutely sufficient[27].Given the power supply constraint,this paper develops existing algorithms to propose deferrable loads control scheduling(DLCS)algorithm to schedule deferrable loads,and a real-time control system will be investigated with the power supply constraint to make full use of power supply resources.

Summarizing the discussions made so far and considering the constraint of power supply,it is of both theoretical significance and practical importance to design a real-time distributed control algorithm with the proposed constrained conditions.This appears to be a challenging task with three essential difficulties identified as follows:1)How to construct an effective objective function under the constraint of power supply?2)Considering the independence and randomness of deferrable loads arrivals,and the unavailable future deferrable loads information,how to model and forecast electric load?3)On the basis of 1)and 2),how to design an effective algorithm to optimize the objective function?It is,therefore,the main motivation of this paper to provide satisfactory answers to the three questions mentioned above and also propose a design scheme of real-time scheduling algorithm.

In the context of imprecise predictions about both future renewable generation and deferrable loads,this paper aims to investigate the real-time control problem for deferrable loads scheduling with power supply constraint based on the previous work.In order to guarantee the effective utilization of power resources,the main contributions of this paper are outlined as follows:1)the objective function of the optimal scheduling problem is designed as the variance of the differences between power supply and aggregate load;2)a mathematical model is established to forecast electric load considering the randomness in renewable generation,and pseudo load is introduced to represent future deferrable load;3)DLCS algorithm is proposed to optimize the objective function and we provide the detail steps of the algorithm;4)the effectiveness of the proposed algorithm is illustrated by simulation experiments.

The rest of this paper is organized as follows:In Section II,we establish mathematical models and transform the real-time scheduling problem with power supply constraint into an optimal control problem.Section III mainly proposes a real-time distributed control algorithm for deferrable loads scheduling according to the control problem and then presents the detailed steps of the algorithm.Simulation results are applied to illustrate the effectiveness of the proposed algorithm in Section IV.Finally,we conclude this paper and give some discussions on future works in Section V.

II.PROBLEM DESCRIPTION

Consider a discrete-time model over a finite time horizon,we divide the scheduling cycle intoTslots of equal length labeled 1,2,...,T.Model objects include renewable generation,non-deferrable load and deferrable load.Furthermore,deferrable loads arrivals are independent and random over time.At the time of decision making,only imprecise predictions about future renewable generation and future load are available.

This section aims to make power consumption schedules for each deferrable load under the constraint of power supply.Accordingly,the power supply curve can be as close as possible to the load curve,and power resources provided by the electricity market can be fully utilized.Ignoring power losses,it can be achieved by optimizing(minimizing)the variance of the differences between power supply and aggregate load.

The objective function is designed as:

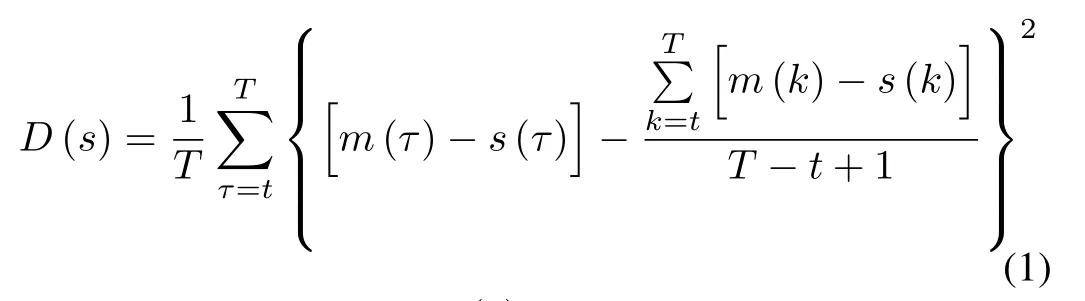
wheret=1,2,...,T,D(s)is the variance of differences between power supply and aggregate load.denotes the power supply schedule,which can be obtained by predicting the consumption curve in power markets.s=is aggregate load schedule and it will be described in detail at a later stage.The aggregate load curve can be obtained by deferrable loads scheduling.can be obtained by minimizingD(s),and the load curve will be the most close one to the power supply curve at this time.

Besides,in(1),the objective functionD(s)can be replaced by a functionwhereF:R→R is strictly convex.

A.Model Overview

Non-deferrable load and renewable generation are denotedbase load It is arduous to and respectively.De fine predict renewable generation,including wind and solar power generation,because of the impact of random fluctuations.So in this section,is considered as a stochastic process,and we use a causal filter based model to establish a stochastic model[26].The structure of the model is shown in Fig.1.

At timet,the predictionbtof base load can be modeled as the sum of its expectationand a random deviationwhere the sequencecan be obtained from historical data and weather report.The sequenceδbcan be modeled as an uncorrelated sequence of identically distributed random variablespassing through a causal filter.In addition,the mean ofxis 0,the variance isσ2.

Fig.1.Structure of the prediction model of base load.

De fine the prediction ofbas:

Considering the causality of the filter,it is obvious thatConsequently,bt(τ)=b(τ)forτ=1,2,...,t.

The causal filter is considered with a finite but fl at impulse response,i.e.,there exist Δ＞0 such that:

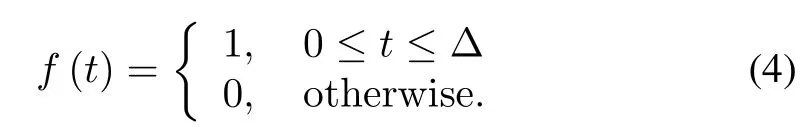
Assumption 1:EVs represent deferrable loads.The sum of EVs that arrive over the scheduling cycle isN,the total power consumption of each EV before a deadline is certain.But the arrival time is uncertain,independent and random.

Based on Assumption 1,for a total ofNdeferrable loads,label them 1,2,...,N.Consider that loadn+1 arrives no earlier than loadnforn=1,2,...,N-1.De fineN(t)as the number of deferrable loads that arrive before or at timet,which satis fiesN(0)=0,N(T)=N(t=1,2,...,T,andNis a constant number).

Definition 1:At timet,vn(t)denotes the power consumption of deferrable loadn.andare de fined as the upper and lower bounds,respectively,i.e,

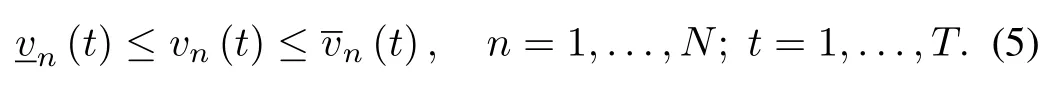
Thenvn={vn(1),...,vn(T)}is the schedule of deferrable loadn,i.e.,its power consumption pro file.

Remark 1:The stepped electricity price for residents is an effective system to make full use of the price leverage.Besides,it is also beneficial to guide residents for the reasonable use of power and energy saving[26].While an EV plugs in with Level II charging,its charging power must be within[0,3.3]kW,i.e.,Therefore,it is obvious that the charging power is 0kW if there is no EV plugs in,i.e.,

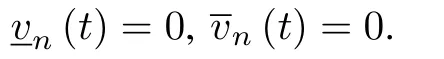
During the scheduling cycle,Vndenotes the total power demand of EVn,which implies that

Letc(t)denote the total power request of all the deferrable loads that arrive at timet(t=1,2,...,T),thec(t)is de fined as the following:

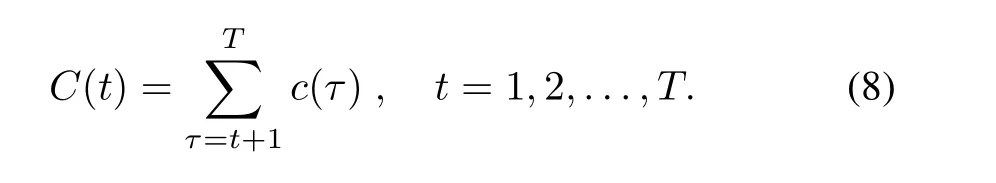
It is worth noting that only information about deferrable load 1 toN(t)is available at timet,which includeInformation about future deferrable loadN(t)+1,...,Nis unavailable and thus we use a pseudo deferrable load to represent the future load.

Definition 2:is the power consumption of pseudo load, fixa(t)=0.andare de fined as the upper and lower bounds respectively.Then it subjects to:

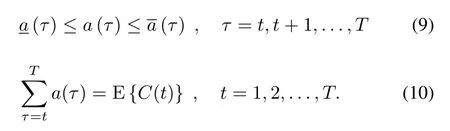
B.Real-time Distributed Optimal Control Problem

Definition 3:Aggregate loadis de fined as:

According to the objective function designed in(1)and the constrains listed above,the load scheduling problem with power supply constraint can be formulated as the following optimal control problem:

Remark 2:In[26],the objective function is designed as the variance of aggregate load,and the aim of scheduling is to realize “valley- filling”to minimize the fluctuations in the load curve.However,it is not fit for this paper as not consider the constraint of power supply.Besides,the objective function of this paper is designed as the variance of the differences between power supply and aggregate load.

According to[28],it can be seen that the optimal solution of the real-time control problem will not change when objective functionD(s)is replaced bywhereF:R→R is strictly convex.Therefore,it’s reasonable that we chooseD(s)as the objective function.

Moreover,if predictions of base load are exact and all deferrable loads arrive at the beginning of a scheduling cycle,i.e.,bt=b,N(t)=N(t=1,2,...,T),then the real-time optimal control reduces to a static optimal control,which has been studied in our previous work.

III.ALGORITHM DESCRIPTION

In order to solve the problem in(12),this section will propose a distributed optimization algorithm:DLCS algorithm,which is iterative until converging to an optimal solution.During each iteration step,a centralized coordinator guides deferrable loads to update their power consumption schedules by means of generating a control signal.

Remark 3:DLCS algorithm is a real-time distributed load control algorithm for deferrable loads scheduling.In addition,a real-time algorithm means that deferrable loads arrive over time and only predictions about future renewable generation and load are available at the time of decision making,and a distributed algorithm means that all EVs can formulate their own charging pro files under the guidance of a centralized coordinator.The power company can become a centralized coordinator in practice.

At timet,the detailed steps of DLCS algorithm are presented as follows:

1)Seti=0.For loadn=1,2,...,N(t),the power consumption schedulev(i)is initialized as follows:

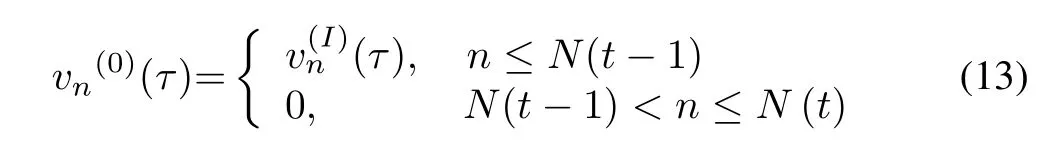
whereis the schedule of loadnin the iterationIof the previous time slot(t-1).

2)For loadN(t)+1,...,N,the pseudo load schedulecan be obtained by minimizing the differences between power supply and aggregate load as follows:

3)The mean of the differences between power supply and aggregate load can be chosen as the control signalc(i):

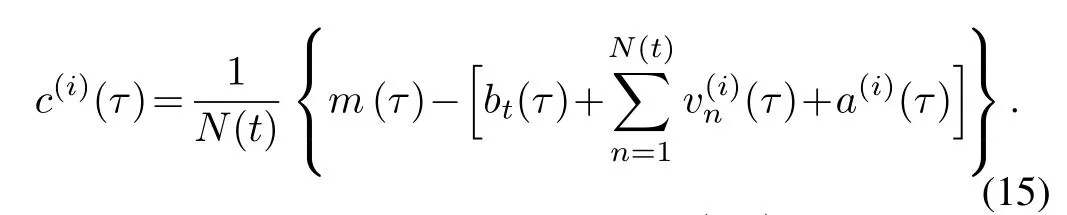
4)For loadn= 1,2,...,N(t),is updated by solving:

5)Seti=i+1.Ifi＜I,then return to 2),else continue 6).

6)UpdateVn(t+1) =Vn(t)-vn(t).For load 1,2,...,N(t),the algorithm outputs their final schedules asvn(t)=(t).Where the superscripts in brackets denote the round of iteration and we setIas the maximum iterations.Final outputs are power consumption schedulesvn={vn(t),vn(t+1),...,vn(T)}of each loadn(n=1,2,...,N(t)).

Remark 4:Reference[26]has proposed a load scheduling algorithm aiming to realize “valley- filling”,and the convergence of its outputs has been proven in the paper.Similarly,it can be proved that,with power supply constraint,the schedules of the deferrable loads obtained by DLCS algorithm converge to the optimal solutions of the optimal control problem.

Fig.2 manifests the information flow between the centralized coordinator and the deferrable loads.According to the control signalcsent by the coordinator,each deferrable load updates its power consumption schedule independently,and delivers the updatedvnback to the coordinator.Then the coordinator alterscto match with the receivedvn.Iterations will not stop until achieving convergence.

Fig.2. Information flow in DLCS algorithm.

IV.SIMULATION RESULTS

This section illustrates the effectiveness of the DLCS algorithm through MATLAB simulation experiments.The scheduling cycle is set from 20:00 on the first day to 20:00 on the next day,the length of a time slot is set as 1 hour,andT=24.We choose 100 households to participate in the experiments,and assume that 20 EVs are available for scheduling,thenN=20.

The traces of non-deferrable load come from the average residential load in the service area of Southern California Edison in 2012[29],we take the mean of 366 days at every time slot and consider the traces are available at the beginning of the time horizon.The traces of renewable generation come from the 10-minute historical data for total wind power generation of the Alberta Electric System Operator from 2004 to 2009[30].In addition,base load is defined as the differences between power supply and aggregate load,the traces of non-deferrable load are precise and thus we consider that the uncertainties in base load only come from renewable generation.

Wind generation is used to represent renewable generation.Uncertainties in wind power generation can be denoted by the error of wind power predictions.Probability distribution of the wind power prediction error includes normal distribution,Weibull distribution,piecewise exponential distribution,and so on.In addition,it presents time-varying features[31].Without loss of generality,this paper uses normal distribution as the distribution model of wind power prediction error.Assume that the prediction error satisfies normal distribution,then the variance is determined by the prediction time scale.

Assumption 2:At timet(1≤t≤T),w(τ)denotes the wind generation of prediction timeτ(τ＞t).The prediction error can be constructed as the sum of a Gauss random sequencexs(τ),the mean is 0,and the variance is set as[26]:then the wind power prediction is:

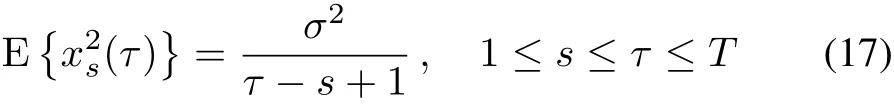
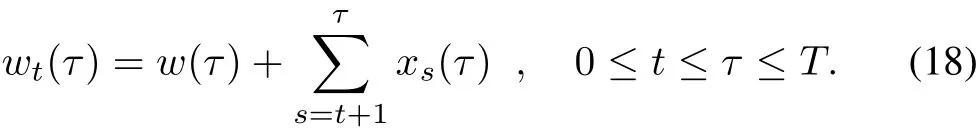
(E{w0(T)-w(T)}2)1/2is the root-mean-square prediction error and it takes 0%-22.5%of the nameplate wind generation capacity in the next 24 hours[32].It only depends on how far ahead the prediction is according to(18).Looking 24 time slots,the normalized wind prediction error curve is manifested in Fig.3,where it can be found that the prediction time interval is shorter,the error is smaller.

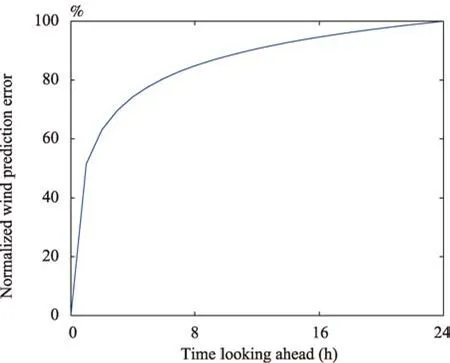
Fig.3.Root-mean-square prediction error over time.

For the sake of simplicity,we assume that all EVs are absolutely identical,and each one requires to consume 10kWh power energy in total and the charging power must within[0,3.3]kW.In addition,the arrival process of the deferrable loads begins at 20:00 on the first day and ends at 12:00 on the next day.After the deadline all EVs have already arrived.In the simulations,the charging behavior of EVs is applied to represent the power consumption behavior of deferrable loads,and the charging curve of EVs is the power consumption schedule of deferrable loads.

Assumption 3:The arrival of each EV is random.At timet(t=1,2,...,T),the prediction of future deferrable load total energy demandE{C(t)}can be denoted as a product of the arrival ratepand the length of the rest of the arrival process(T0-t)[26].T0is the deadline of EVs arrival,and we takeT0=16,then:

Furthermore,t＞T0means the deferrable load arrival process has ended,i.e.,E{C(t)}=0.

Experiments demonstrate that DLCS algorithm converges fairly fast,and iterations will stop after 15 rounds.The algorithm proposed in[26],denoted as VF algorithm,would be optimal when ignoring the constraint of power supply.Simulation results obtain the power consumption schedules of deferrable loads at every time slot.We compare the load curves of DLCS algorithm with VF algorithm in the case thatt=4(0:00),t=8(4:00)andt=12(8:00),respectively.

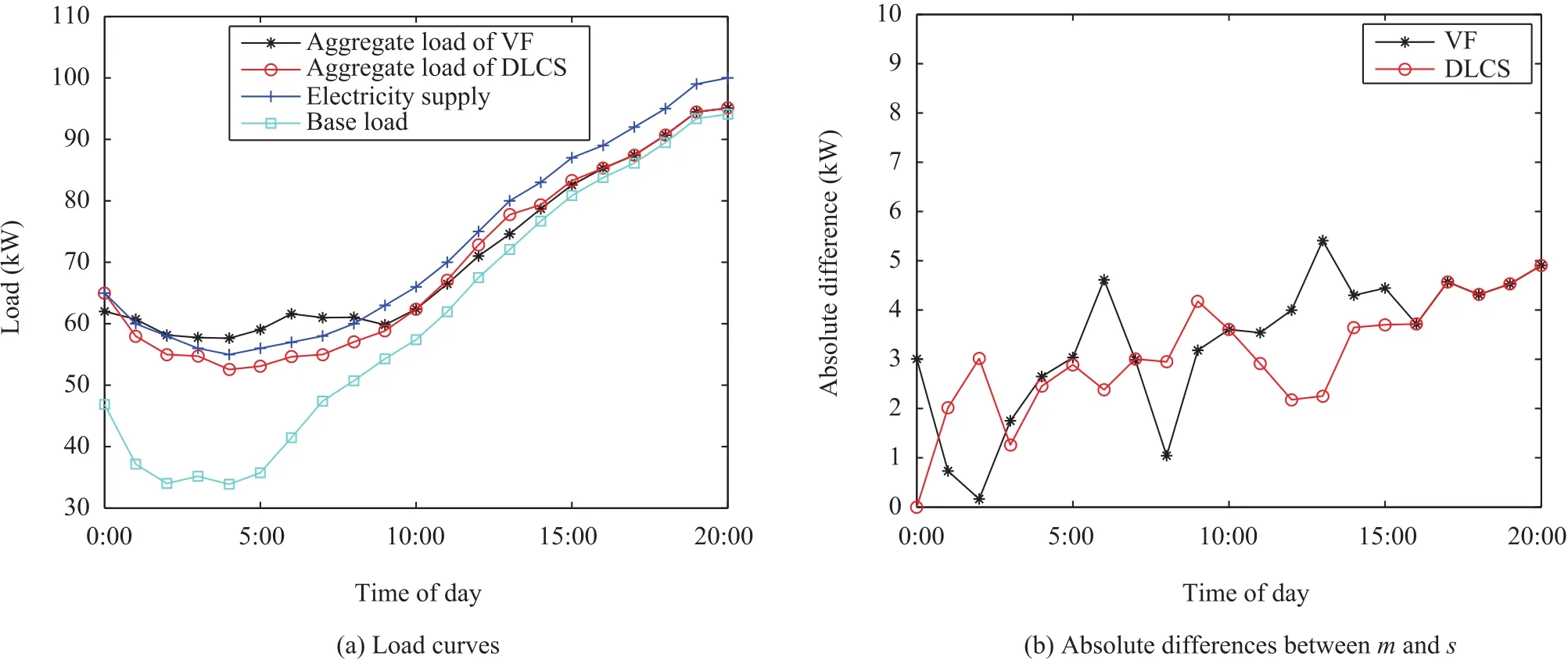
Fig.4.Comparison between DLCS algorithm and VF algorithm(t=4).

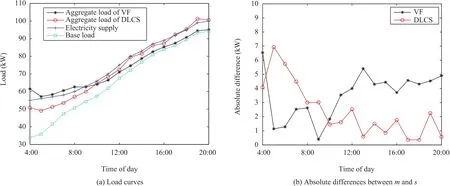
Fig.5.Comparison between DLCS algorithm and VF algorithm(t=8).

Figs.4(a),5(a)and 6(a)display the scheduling results of DLCS algorithm and VF algorithm with scheduling timettaking different values.On the one hand,as the aim of VF algorithm for deferrable loads scheduling is to minimize the variance of aggregate load,it is worth noting that the aggregate loadsof VF algorithm in three time periods(1:00-8:00 in Fig.4(a),4:00-9:00 in Fig.5(a)and 8:00-8:40 in Fig.6(a))have already exceeded the power supplym.It would lead to over-demand in power systems.On the other hand,the three figures manifest that aggregate load of DLCS algorithm is invariably lower than power supply except for individual time points(18:00-20:00 in Fig.5(a))and accordingly DLCS algorithm can avoid the over-load effectively.In summary,compared with VF algorithm,the aggregate load curve obtained by DLCS algorithm is more close to the power supply curve,and it has a stronger potential to track the power supply curve.

At different scheduling time slots,Figs.4(b),5(b),6(b)present two curves of the absolute differences between power supplymand aggregate loads,and these curves are obtained by the two different algorithms respectively.These figures demonstrate that the differences of DLCS algorithm always keep in a lower level and have smaller fluctuations when compared with VF algorithm.The amount of remaining unused power energy obtained by DLCS algorithm is smaller as well,and it is beneficial to avoid the waste of resources.

The above conclusion can be verified from Table I which demonstrates the mean and the variance of absolute differences obtained by the two algorithms at different time slots.From the comparison between the third and fourth columns,it can be found that the mean and the variance of DLCS algorithm are invariably smaller than VF algorithm.It shows that DLCS algorithm has a higher utilization of power resources.All of the above simulation results manifest that,it’s more effective to use DLCS algorithm for real-time deferrable loads scheduling control under the constraint of power supply.

Fig.6.Comparison between DLCS algorithm and VF algorithm(t=12).

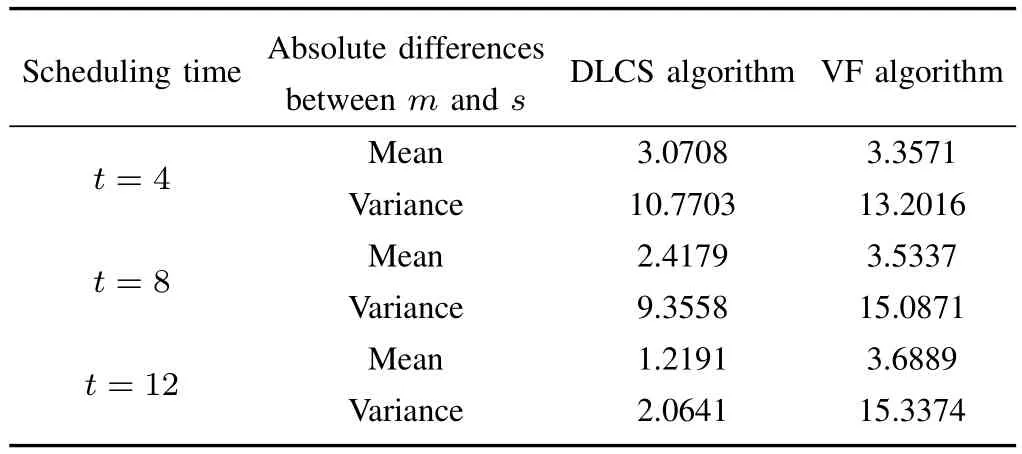
TABLE ICOMPARISON BETWEEN THE TWO ALGORITHMS

V.CONCLUSIONS AND FUTURE WORKS

To conclude,this paper has studied the real-time distributed control for deferrable loads scheduling problem considering the constraint of power supply.By designing the objective optimization function with power supply constraint,and establishing a load forecasting model with uncertainties,we transform the load scheduling problem into an optimal control problem,and propose DLCS algorithm to handle this problem.The aim of scheduling is to make aggregate load curve approach to power supply curve as far as possible.In addition,detailed steps of DLCS algorithm have also been presented in the paper.The effectiveness of DLCS algorithm has been verified compared with the existing VF algorithm in the simulation results.Besides,as VF algorithm only can be available in the ideal condition without being restrained by power supply,DLCS algorithm has overcome this limitation and obtained a stronger practicality.And the utilization of power supply resources is more reasonable by choosing DLCS algorithm for real-time scheduling.

However,DLCS algorithm also has its limitation.For example,it only focuses on optimization effect of the aggregate load curve,and ignores the potential impact that deferrable loads scheduling may incurs on power flow and voltage of power systems.Since there are different types of deferrable loads,it should consider that various loads require different power consumptions.Besides,in this paper,we only view the deferrable loads as one kind of power consumption components.However,some certain deferrable loads,such as EVs,can become energy storing devices.They can consume and store energy in load-valley,and then release energy in load-peak to regulate load curves.In a word,under the constraint of power supply,the real-time distributed optimal control for deferrable loads scheduling is worth of making a further research.

[1]M.Z.Jacobson,M.A.Elucchi,and M.A.Cameron,“Low-cost solution to the grid reliability problem with 100%penetration of intermittent wind,water,and solar for all purposes,”Proc.of the National Academy of Sci.,vol.112,no.49,pp.150–165,2015.

[2]M.Caramanis and J.M.Foster,“Management of electric vehicle charging to mitigate renewable generation intermittency and distribution network congestion,”inProc.48th IEEE Conf.Decision and Control,2009 Held Jointly with the 2009 28th Chinese Control Conference,Shanghai,China,2009,pp.4717-4722.

[3]M.Duvall and E.Knipping,“Environmental assessment of plug-in hybrid electric vehicles,”Electric Power Research Institute,Palo Alto,CA,USA,2007.

[4]J.G.Yao,S.C.Yang,K.Wang,Z.L.Yang,and X.F.Song,“Concept and research framework of smart grid “source-grid-load”interactive operation and control,”Automat.Electr.Power Syst.,vol.36,no.21,pp.1-6,12,Nov.2012.

[5]J.Xie,K.Wang,D.H.Feng,D.Zeng,Y.P.Li,and D.Yue,“A security-constrained flexible demand scheduling strategy for wind power accommodation,”Int.Trans.Electr.Energy Syst.,vol.26,no.6,pp.1171-1183,Jun.2016.

[6]C.Yammani,S.Maheswarapu,and S.K.Matam,“Optimal placement and sizing of distributed generations using shuffled bat algorithm with future load enhancement,”Int.Trans.Electr.Energy Syst.,vol.26,no.2,pp.274-292,Feb.2016.

[7]J.H.Zheng,X.Y.Wang,and S.Z.Zhu,“A novel real-time load modeling method for fast large-disturbance and short-term voltage stability analysis,”Int.Trans.Electr.Energy Syst.,vol.23,no.8,pp.1373-1395,Nov.2013.

[8]L.Kelly,A.Rowe,and P.Wild,“Analyzing the impacts of plug-in electric vehicles on distribution networks in British Columbia,”inProc.2009 IEEE Electrical Power&Energy Conf.(EPEC),Montreal,QC,Canada,2009,pp.1-6.

[9]C.Roe,E.Farantatos,J.Meisel,A.P.Meliopoulos,and T.Overbye,“Power system level impacts of PHEVs,”inProc.IEEE 42nd Hawaii International Conf.System Sciences,Big Island,HI,USA,2009,1-10.

[10]K.Clement,E.Haesen,and J.Driesen,“Coordinated charging of multiple plug-in hybrid electric vehicles in residential distribution grids,”inProc.IEEE/PES Power Systems Conf.Exposition,Seattle,WA,USA,2009,1-7.

[11]J.A.P.Lopes,F.J.Soares,and P.M.R.Almeida,“Integration of electric vehicles in the electric power system,”Proc.IEEE,vol.99,no.1,pp.168-183,Jan.2011.

[12]P.Denholm and W.Short,“An evaluation of utility system impacts and bene fits of optimally dispatched plug-in hybrid electric vehicles,”National Renewable Energy Laboratory,Tech.Rep.NREL/TP-620-40293,Jul.2006.

[13]C.Quinn,D.Zimmerle,and T.H.Bradley,“The effect of communication architecture on the availability,reliability,and economics of plug-in hybrid electric vehicle-to-grid ancillary services,”J.Power Sources,vol.195,no.5,pp.1500-1509,Mar.2010.

[14]J.A.P.Lopes,F.J.Soares,P.M.Almeida,and M.M.da Silva,“Smart charging strategies for electric vehicles:enhancing grid performance and maximizing the use of variable renewable energy resources,”inProc.24th International Battery,Hybrid and Fuel Cell Electric Vehicle Symposium and Exhibition,Stavanger,Norway,2009,pp.1-11.

[15]L.W.Gan,U.Topcu,and S.H.Low,“Stochastic distributed protocol for electric vehicle charging with discrete charging rate,”inProc.2012 IEEE Power and Energy Society General Meeting,San Diego,CA,Chile,2012,pp.1-8.

[16]Y.Y.Hsu and C.C.Su,“Dispatch of direct load control using dynamic programming,”IEEE Trans.Power Syst.,vol.6,no.3,pp.1056-1061,Aug.1991.

[17]Z.J.Ma,D.S.Callaway,and I.A.Hiskens,“Decentralized charging control for large populations of plug-in electric vehicles,”inProc.49th IEEE Conf.Decision and Control,Atlanta,GA,USA,2010,pp.206-212.

[18]D.J.Aigner and J.G.Hirschberg,“Commercial/industrial customer response to time-of-use electricity prices:some experimental results,”RAND J.Econ.,vol.16,no.3,pp.341-355,Sep.1985.

[19]L.J.Chen,N.Li,S.H.Low,and J.C.Doyle,“Two market models for demand response in power networks,”inProc.First IEEE International Conf.Smart Grid Communications,Gaithersburg,MD,USA,2010,pp.397-402.

[20]N.Li,L.J.Chen,and S.H.Low,“Optimal demand response based on utility maximization in power networks,”inProc.2011 IEEE Power and Energy Society General Meeting,Detroit,MI,USA,2011,pp.1-8.

[21]M.Ilic,J.W.Black,and J.L.Watz,“Potential bene fits of implementing load control,”inIEEE Power Engineering Society Winter Meeting,New York,NY,USA,vol.1,pp.177-182,2002.

[22]A.J.Conejo,J.M.Morales,and L.Baringo,“Real-time demand response model,”IEEE Trans.Smart Grid,vol.1,no.3,pp.236-242,Dec.2010.

[23]S.Deilami,A.S.Masoum,P.S.Moses,and M.A.S.Masoum,“Realtime coordination of plug-in electric vehicle charging in smart grids to minimize power losses and improve voltage pro file,”IEEE Trans.Smart Grid,vol.2,no.3,pp.456-467,Sep.2011.

[24]S.Y.Chen and L.Tong,“iEMS for large scale charging of electric vehicles:Architecture and optimal online scheduling,”inProc.3th IEEE International Conf.Smart Grid Communications(Smart Grid Comm),Tainan,China,2012,pp.629-634.

[25]S.Deilami,A.S.Masoum,P.S.Moses,and M.A.S.Masoum,“Realtime coordination of plug-in electric vehicle charging in smart grids to minimize power losses and improve voltage pro file,”IEEE Trans.Smart Grid,vol.2,no.3,pp.456-467,Sep.2011.

[26]L.W.Gan,A.Wierman,U.Topcu,N.J.Chen,and S.H.Low,“Realtime deferrable load control:handling the uncertainties of renewable generation,”inProc.4th International Conf.Future Energy Systems,Berkeley,California,USA,2013,pp.113-124.

[27]C.Y.Wu,“Promotion of the stepped price for residential electricity use in Zhejiang province:existing problems and countermeasures,”Energy Technol.Econ.,vol.23,no.5,pp.48-52,May 2011.

[28]L.W.Gan,U.Topcu,and S.H.Low,“Optimal decentralized protocol for electric vehicle charging,”IEEE Trans.Power Syst.,vol.28,no.2,pp.940-951,May 2013.

[29]E.Sortomme,M.M.Hindi,S.D.J.Macpherson,and S.S.Venkata,“Coordinated charging of plug-in hybrid electric vehicles to minimize distribution system losses,”IEEE Trans.on Smart Grid,vol.2,no.1,pp.198-205,2002.

[30]A.Subramanian,M.Garcia,A.Dominguez-Garcia,and D.Callaway,“Real-time scheduling of deferrable electric loads,”inProc.2012 IEEE American Control Conference,Japan,pp.3643-3650.

[31]S.Y.Wang,B.J.Li,J.L.Yu,and T.S.Xu,“Analysis on time-varying characteristics of probability error in forecast of wind speed and wind power,”Power Syst.Technol.,vol.37,no.4,967-973,Apr.2013.

[32]A.Bemporad and M.Morari,“Robust model predictive control:a survey,”Robustness in identification and control,Springer London,pp.207-226,1999.