Stabilization of Uncertain Systems With Markovian Modes of Time Delay and Quantization Density

Jufeng Wang and Chunfeng Liu

I.INTRODUCTION

FOUR-wheel independently actuated vehicles in which each wheel is independently actuated by an in-wheel motor,have attracted increasing research efforts in recent years due to their actuation flexibility and fast speed.As is well known,stability is an important problem to be considered in system analysis and design.To ensure the stability of vehicle lateral motion,the study on lateral motion control has been actively conducted since effective lateral motion control can prevent unintended vehicle behavior.

In[1],through an analytical method,a vehicle lateral-plane motion stability control approach is presented.In[2],a control law combined with a stabilization algorithm of the yaw motion is given based on a robot dynamic model.To maintain lateral stability,there are various controllers proposed,such as a sliding mode controller[3],a state observer[4]and an output constrained controller[5].Nevertheless,the results in them cannot be applied to the networked control systems(NCSs)whose plants,controllers and actuators are located at different places,and signals are transmitted from one place to another through communication networks.

With the very rapid advances in communication network,NCSs have gained wide applications in modern vehicles[6]-[8].Compared to the traditional control systems,NCSs have many advantages such as system flexibility and reduced cost.Despite such advantages,the use of communication networks makes the system analysis more complicated.

Owing to bandwidth limitation,data cannot be sent with in finite precision in communication networks.To reduce network congestion,quantizers are always used in a signal transmission process.In[9]-[11],the stabilization of linear time-invariant systems with quantization is investigated.Nevertheless,time delay is not taken into account.

In practice,time delay always occurs since sampling data is transmitted through a network,and it may cause system instability.Therefore,the stabilization problem of NCSs with time delay has attracted much research[12]-[16].In many cases,time delay is random and can be modeled as Markov chains[17]-[22].In[17],the state-feedback controller’s gain is constant.This controller is called a mode-independent controller in our paper.In[18]-[22],a feedback controller that depends on time delay is designed.We call such controller that depends on physical variables,e.g.,time delay and quantization density,as a mode-dependent controller.

Compared to NCSs with only time delay or quantization,it is more difficult to analyze those with both time delay and quantization.In[23]-[28],the latter are studied,but their feedback controllers are all static and controlled plants are all deterministic systems.As is well known,the stability condition of a system with mode-dependent controller is less conservative than that of a system with a mode-independent controller.Meanwhile,due to interference,the parameters of vehicle lateral dynamics,e.g.,longitudinal speed and cornering stiffness coefficients,are subject to change.Such change may destroy the stability of otherwise stable closed-loop lateral motion systems.If only a deterministic model of a vehicle lateral dynamics is considered in system analysis,the resultant system may exhibit a high degree of vulnerability.Accordingly,in this paper,we model the vehicle lateral dynamics as an uncertain system.

It should be pointed out,the stabilization problem of NCSs with time delay and quantization has not been fully investigated,and most of the results in the existing literature are focused on sufficient conditions for the stability of NCSs.It is worth mentioning that sufficient and necessary conditions for the stability of NCSs have been studied in[18]-[20].However,the plant studied in the literature mentioned above is a deterministic system or a Markovian jump linear system.Moreover,the controller design considers time delay only but not quantization.Therefore,the results cannot be directly applied to our case where the plant is an uncertain lateral motion system having time delay and quantization error.To the authors’best knowledge,the stabilization of vehicle lateral motion with time delay and quantization has not been fully investigated,especially the sufficient and necessary conditions for the stability of uncertain lateral motion systems having time delay and quantization density with Markovian characterization.This fact motivates the present study.

This work for the first time studies the stabilization of vehicle lateral motion subject to both quantization and time delay.The lateral motion of independently actuated four-wheel vehicle is modelled as an uncertain system.To incorporate the correlation between the current time delay(quantization density)and time delay(quantization density)in the next transmission,the quantization density and time delay are modeled as two homogeneous Markov chains.The sufficient and necessary conditions for the stochastic stability of networked vehicle lateral motion are derived under an output-feedback controller that depends on the modes of time delay and quantization density.A practical lateral motion example is presented to demonstrate the effectiveness of the proposed controller.

II.NETWORKED CONTROL SYSTEM MODEL

The structure of our concerned NCS is shown in Fig.1.Its plant is vehicle lateral dynamics shown in Fig.2[22].A two-degree-of-freedom model is adopted to describe the plant.With the fact that side slip angle,steering angle and lateral acceleration are small,the tire lateral forceFyf(Fyr)is approximately linear with the tire slip angleαf(αr),and the state-space model of the lateral motion control can be approximately written as[4],[22]

Fig.1. The structure of NCS.

Fig.2. Vehicle lateral dynamics.

where

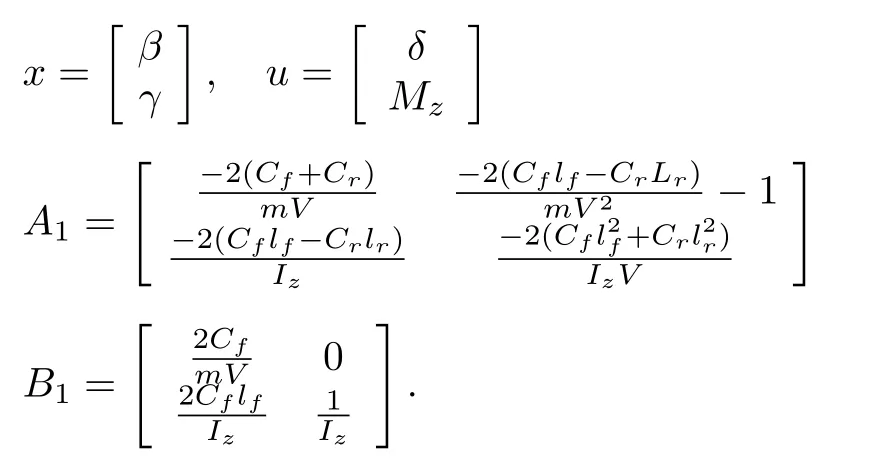
Here,y(t)is the output of the plant,C1is a constant matrix of appropriate dimensions,γis the yaw-rate,mis the vehicle mass,Vis the longitudinal speed,Mzis the yaw moment,δis the front wheel steering angle,CfandCrare the cornering stiffness of each front tire and rear tire,Izis the vehicle yaw inertia,andlfandlrare the distances from the front and rear axles to the center of gravity.

In the NCS,the sensor,controller and actuator are all time-driven.With a sampling periodT,the continuous state-space model(1)can be transformed into a discrete one as follows[29]:

where

From the process of modeling,we know that model(2)well describes the actual vehicle lateral dynamics,and is affected by parametric uncertainties(e.g.,the uncertainties on the longitudinal speed and cornering stiffness coefficients).In order to consider the model approximation and model parameter uncertainty,we modify the discrete-linear system(2)into a discrete-uncertain system described by

where ΔA(k)and ΔB(k)are unknown matrices representing the time-varying norm-bounded uncertainties that satisfy the following condition

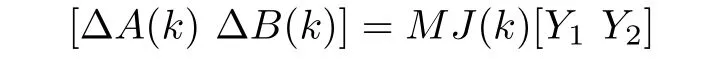
whereM,Y1andY2are known real constant matrices with appropriate dimensions,andJ(k)is the unknown time-varying matrix function subject toJ(k)TJ(k)≤I.In Fig.1,τkrepresents the sensor-to-controller delay,andq(·,σk)stands for the quantizer with quantization densityρσk,0＜ρσk＜1,σk∈N+η={1,2,...,η}.η∈N+={1,2,...}.LetN={0,1,2,...},the set of natural numbers,and the value ofσkcorresponds to that ofρσk.To ease the network congestion,the quantization density is designed to be a function of the network load which is related to the network induced delay[30].Considering the correlation between the current time delay(quantization density)and time delay(quantization density)in the next transmission,τkandσk(ρσk)are modeled as two homogeneous Markov chains that take values inNτ={0,1,...,τ},τ∈NandN+η({ρ1,ρ2,...,ρη}),respectively.Their transition probability matrices are Γ =[λlh]and Ξ =[αij],respectively.τkandσk(ρσk)jump from modesltohand from modesi(ρi)toj(ρj)with probabilitiesλlhandαij,respectively

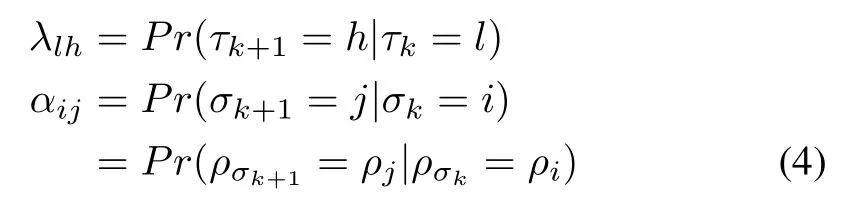
whereλlh,αij≥0 and

The quantizerq(y,j)is proposed as follows:

Let the quantization densityρin[23]equalρj.We can then describe the corresponding set of quantization levels of quantizerq(y,j)as follows:

The correspondingql(yl,j)is de fined as follows:

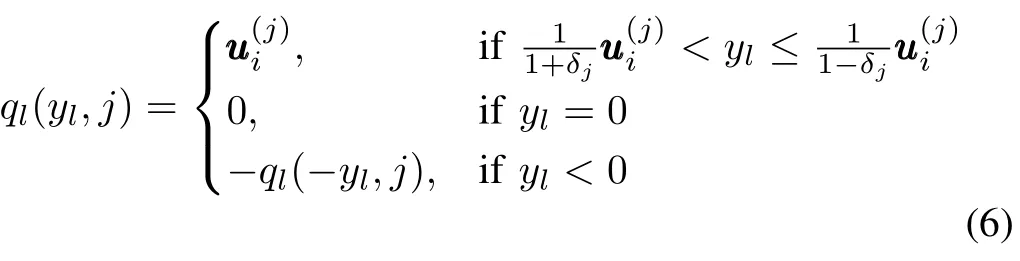
withδj=(1-ρj)/(1+ρj).

From(6),q(y(k),j)can be rewritten as

whereH(j)is an uncertain diagonal matrix satisfying

Considering the time delay,we have

De fine

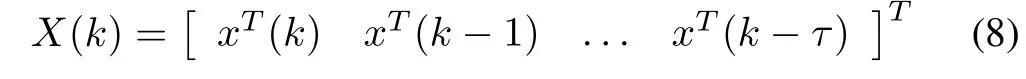
then,we have

where

Cis the(1+τk)th block of(τk).

A two-mode-dependent output-feedback controller is designed as

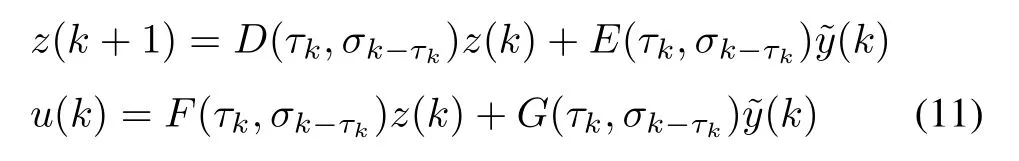
wherez(k)∈Rn,D(τk,σk-τk),E(τk,σk-τk),F(τk,σk-τk)andG(τk,σk-τk)are appropriately dimensioned matrices.

From(9),it is easy to see that

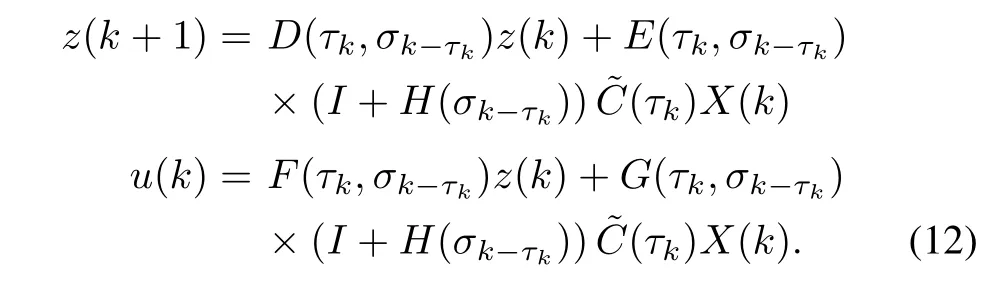
De fine

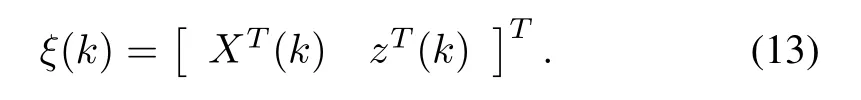
Combining(9)and(12)leads to the following closed-loop system

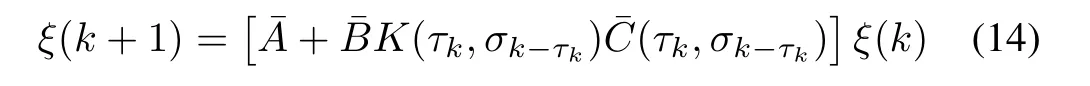
where

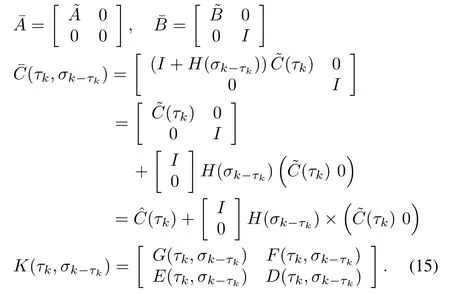
where

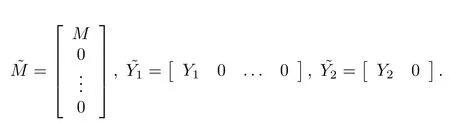
Definition 1[19]:The closed-loop system in(14)is stochastically stable if given every initial conditionξ0=ξ(0),σ-τ0andτ0∈Nτ,there exists a symmetric and positive de finite matrixWsuch that the following holds:

Lemma 1[31]:Given matricesQ,HandEof appropriate dimensions withQbeing symmetrical,Q+HFE+ETFTHT＜0 for allFsatisfyingFTF≤I,if and only if there exists some scalarε＞0,such that

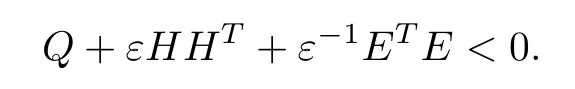
III.MAIN RESULTS

The following theorem gives sufficient and necessary conditions for the stochastic stability of closed-loop networked lateral motion system under the proposed controller(11).Its proof is motivated by the proof in[19]and is given in Appendix.

Theorem 1:Closed-loop system(14)is stochastically stable if and only if there exists a symmetric and positive definite matrixP(l,i)such that

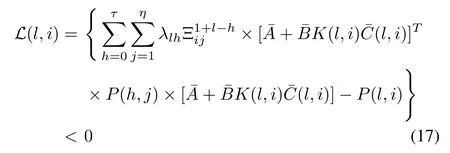
holds for alll∈Nτandi∈N+η.

Based on the results in Theorem 1,the controller design techniques are given in Theorem 2.

Theorem 2:The system in(14)is stochastically stable if and only if there exist positive scalars†ι,ς(l,i),γι,ς(l,i),ει,ς(l,i)(ι=0,1,...,τ,ς=1,2,...,η),a symmetric and positive de finite matrixP(l,i)and a matrixK(l,i)of appropriate dimensions,such that(18)(show at the bottom of this page)holds where

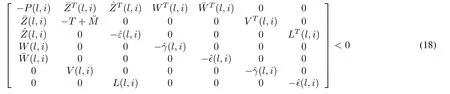
for alll∈Nτandi∈N+η.

Proof:By applying the Schur complement,we obtain that(17)is equivalent to the following inequality:

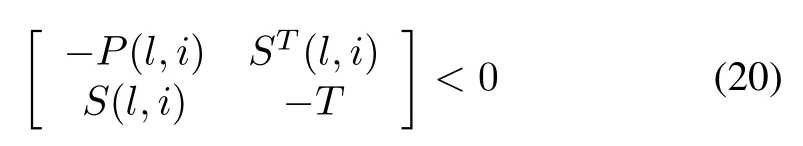
for alll∈Nτand,with

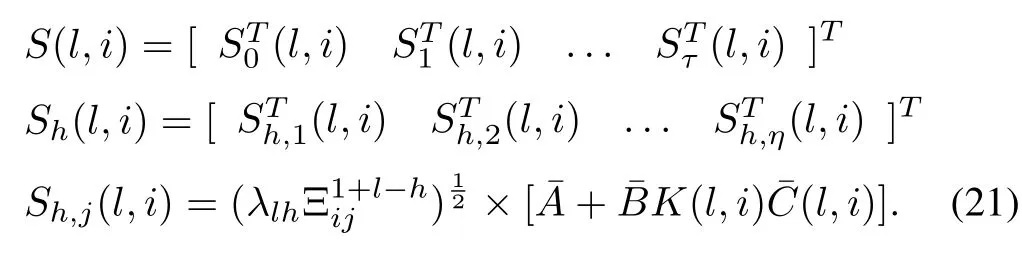
From Lemma 1 and the Schur complement,it is found that the inequality(20)holds if and only if there exist positive scalarsει,ς(l,i)(ι=0,1,...,τ,ς=1,2,η),such that

where

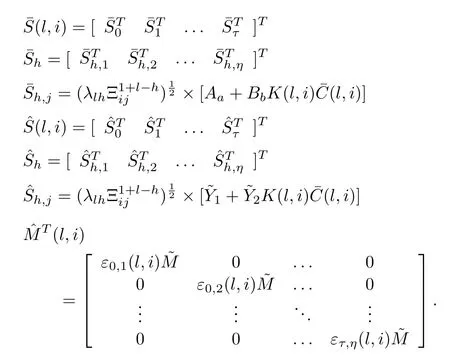
According to the Schur complement,(22)can be rewritten as

By using Lemma 1 and the Schur complement,we conclude that(23)is equivalent to(18).From Theorem 1,we complete the proof. ¥

The conditions in Theorem 2 form a set of linear matrix inequalities with some inversion constraints.K(l,i)can be solved by an iterative linear matrix inequality approach which is called as the cone complementarity linearization algorithm whose detail can be found in[32].Accordingly,D(l,i),E(l,i),F(l,i)andG(l,i)can be obtained from(15).Next,we give an example to show the performance of the proposed controller.

IV.NUMERICALEXAMPLE

Consider a vehicle lateral motion system in(3)with the following parameters[22]

m=800kg,Iz=728.6kg.m2,lf=0.85m

lr=1.04m,Cf=Cr=10000N/rad,V=100km/h.

The parameters of unknown matrices ΔA(k)and ΔB(k)are assumed as

The sampling period of the sensor,controller and actuator is set asT=0.01s.The network time delay is supposed to beτk∈{0,1},that means time delay in a practical vehicle control system is 0T=0s and 1T=0.01s,and its transition probability matrix is given as

The quantizer parameters are set as

Thus we have two different quantization density valuesρ1andρ2.The transition probability matrix ofσk(ρσk)is

The output matrix is

The controller design in[19]considers neither quantization in the network environment,nor uncertainty of the system model parameters.Therefore,the approach of the controller design cannot be applied to our case.

By using Theorem 2,we obtain

Suppose that the initial conditions arex(0)=[3,2],τ0=0 andσ0=1.One of the possible realizations of the random modesσkandτkis shown in Figs.3 and 4,and the realization of the unknown time-varying matrixJ(k)is set to sin(k).Under them,the corresponding state trajectories of the closedloop system are shown in Fig.5.We can clearly see that the closed-loop system is stochastically stable.

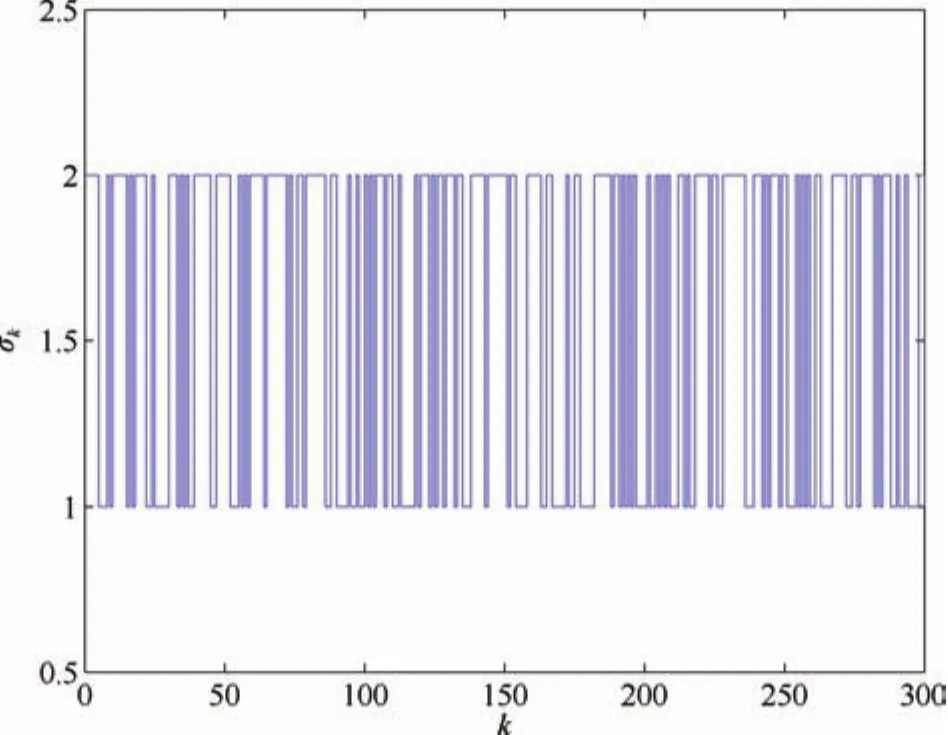
Fig.3.Random mode σk.

Fig.4.Random mode τk.

Fig.5. State trajectories of the closed-loop system.

V.CONCLUSION

The stabilization problem of uncertain-linear vehicle-lateral motion systems over networks is challenging.This work adopts Markov chains to model the stochastic changes of quantization density and time delay modes.These modes are simultaneously incorporated into the output feedback controller design.By constructing a Lyapunov function and Schur complement,this work derives sufficient and necessary conditions of stochastic stability of a given networked vehicle-lateral-motion control system in the form of a set of linear matrix inequalities with some inversion constraints.The cone complementarity linearization algorithm is employed to obtain the desired two-mode-dependent controller.The future work should address the complexity issues when a system or Markov model is of large scale.

APPENDIX

Proof:

Sufficiency:Construct the following Lyapunov function

Then

Let

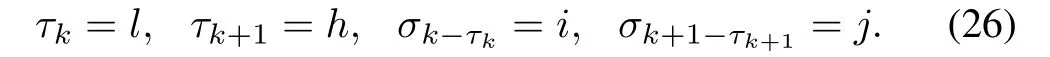
Then,the probability transition matrices are

and

Thus ifL(l,i)＜0,then

whereα=inf{λmin(-L(l,i)}＞0.

It follows from(28)that for anyn≥1,

Furthermore,we have

By using Definition 1,the closed-loop system in(14)is stochastically stable.

Necessity:Assume thatQ(τk,σk-τk)is a symmetric and positive de finite matrix and˜P(T-t,τt,σt-τt)is a symmetric matrix.De fine

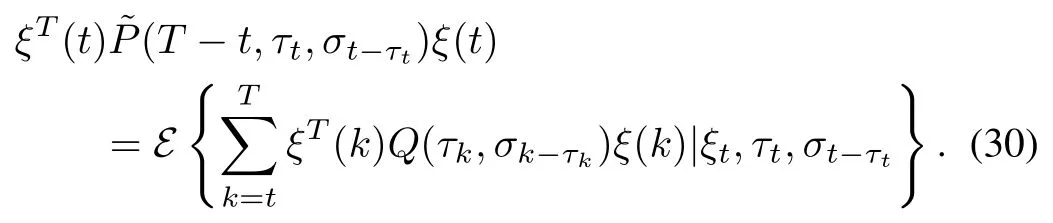
SinceQ(τk,σk-τk)＞0,asTincreases,ξT(t)(T-t,τt,σt-τt)ξ(t)increases.From(16),ξT(t)˜P(T-t,τt,σt-τt)ξ(t)is upper bounded.Furthermore,its limit exists and can be expressed as

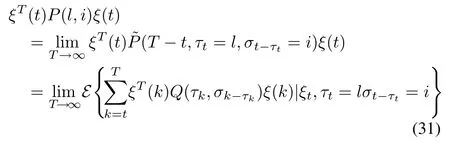
whereP(l,i)is a symmetric matrix.

Thus,we have

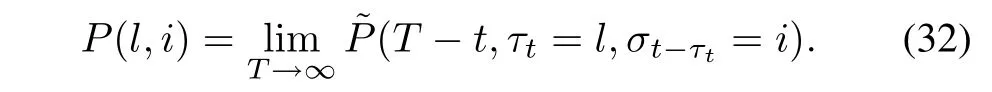
From(31),we obtainP(l,i)＞0 sinceQ(τk,σk-τk)＞0.

From(30),we have

From(14),we have

It is easy to obtain from(33)and(34)that

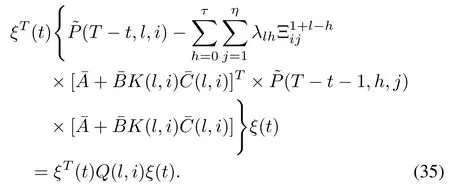
LettingT→∞in(35)and noticing(32),we prove that(17)holds. ¥

[1]R.R.Wang,H.Zhang,J.M.Wang,F.J.Yan,and N.Chen,“Robust lateral motion control of four-wheel independently actuated electric vehicles with tire force saturation consideration,”J.Franklin Inst.,vol.352,no.2,pp.645-668,Feb.2015.

[2]E.Lucet,R.Lenain,and C.Grand,“Dynamic path tracking control of a vehicle on slippery terrain,”Contr.Eng.Pract.,vol.42,pp.60-73,Sep.2015.

[3]H.Alipour,M.Sabahi,and M.B.B.Shari fian,“Lateral stabilization of a four wheel independent drive electric vehicle on slippery roads,”Mechatronics,vol.30,pp.275-285,Sep.2015.

[4]K.Nam,H.Fujimoto,and Y.Hori,“Lateral stability control of in-wheelmotor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors,”IEEE Trans.Vehicul.Technol.,vol.61,no.5,pp.1972-1985,Jun.2012.

[5]C.Hu,R.R.Wang,F.J.Yan,and N.Chen,“Output constraint control on path following of four-wheel independently actuated autonomous ground vehicles,”IEEE Trans.Vehicul.Technol.,vol.65,no.6,pp.4033-4043,Jun.2016.

[6]C.F.Caruntu,M.Lazar,R.H.Gielen,P.P.J.van den Bosch,and S.Di Cairano,“Lyapunov based predictive control of vehicle drivetrains over can,”Contr.Eng.Pract.,vol.21,no.12,pp.1884-1898,Dec.2013.

[7]T.Herpel,K.-S.Hielscher,U.Klehmet,and R.German,“Stochastic and deterministic performance evaluation of automotive can communication,”Computer Networks,vol.53,no.8,pp.1171-1185,Jun.2009.[8]Z.B.Shuai,H.Zhang,J.M.Wang,J.Q.Li,and M.G.Ouyang,“Lateral motion control for four-wheel-independent-drive electric vehicles using optimal torque allocation and dynamic message priority scheduling,”Contr.Eng.Pract.,vol.24,pp.55-66,Mar.2014.

[9]Y.Y.Zou,J.Lam,Y.G.Niu,and D.W.Li,“Constrained predictive control synthesis for quantized systems with Markovian data loss,”Automatica,vol.55,pp.217-225,May 2015.

[10]G.X.Gu and L.Qiu,“Networked control systems for multi-input plants based on polar logarithmic quantization,”Syst.Contr.Lett.,vol.69,pp.16-22,Jul.2014.

[11]C.Liu and F.Hao,“Dynamic output-feedback control for linear systems by using event-triggered quantisation,”IET Contr.Theor.Appl.,vol.9,no.8,pp.1254-1263,May 2015.

[12]X.J.Chen and T.D.Ma,“Parameter estimation and topology identification of uncertain general fractional-order complex dynamical networks with time delay,”IEEE/CAA J.Autom.Sinica,vol.3,no.3,pp.295-303,Jul.2016.

[13]X.-M.Sun,D.Wu,G.-P.Liu,and W.Wang,“Input-to-state stability for networked predictive control with random delays in both feedback and forward channels,”IEEE Trans.Ind.Electron.,vol.61,no.7,pp.3519-3526,Jul.2014.

[14]Z.-H.Pang,G.-P.Liu,D.H.Zhou,and D.H.Sun,“Data-based predictive control for networked nonlinear systems with network-induced delay and packet dropout,”IEEE Trans.Ind.Electron.,vol.63,no.2,pp.1249-1257,Feb.2016.

[15]K.Lee and R.Bhattacharya,“Stability analysis of large-scale distributed networked control systems with random communication delays:a switched system approach,”Syst.Contr.Lett.,vol.85,pp.77-83,Nov.2015.

[16]F.Zhou,L.Liu,and G.Feng,“Fuzzy decentralized control for a class of networked systems with time delay and missing measurements,”Asian J.Contr.,vol.17,no.1,pp.84-98,Jan.2015.

[17]L.Qiu,Q.Luo,F.Gong,S.B.Li,and B.G.Xu,“Stability and stabilization of networked control systems with random time delays and packet dropouts,”J.Franklin Inst.,vol.350,no.7,pp.1886-1907,Sep.2013.

[18]L.Q.Zhang,Y.Shi,T.W.Chen,and B.Huang,“A new method for stabilization of networked control systems with random delays,”IEEE Trans.Automat.Contr.,vol.50,no.8,pp.1177-1181,Aug.2005.

[19]Y.Shi and B.Yu,“Output feedback stabilization of networked control systems with random delays modeled by Markov chains,”IEEE Trans.Automat.Contr.,vol.54,no.7,pp.1668-1674,Jul.2009.

[20]J.F.Wang,C.F.Liu,and H.Z.Yang,“Stability of a class of networked control systems with Markovian characterization,”Appl.Math.Modell.,vol.36,no.7,pp.3168-3175,Jul.2012.

[21]R.N.Yang,G.-P.Liu,P.Shi,C.Thomas,and M.V.Basin,“Predictive output feedback control for networked control systems,”IEEE Trans.Ind.Electron.,vol.61,no.1,pp.512-520,Jan.2014.

[22]X.Y.Zhu,H.Zhang,J.M.Wang,and Z.D.Fang,“Robust lateral motion control of electric ground vehicles with random network-induced delays,”IEEE Trans.Vehicul.Technol.,vol.64,no.11,pp.4985-4995,Nov.2015.

[23]R.N.Yang,P.Shi,G.-P.Liu,and H.J.Gao,“Network-based feedback control for systems with mixed delays based on quantization and dropout compensation,”Automatica,vol.47,no.12,pp.2805-2809,Dec.2011.[24]K.Liu,E.Fridman,K.H.Johansson,and Y.Q.Xia,“Quantized control under round-robin communication protocol,”IEEE Trans.Ind.Electron.,vol.63,no.7,pp.4461-4470,Jul.2016.

[25]K.Liu,E.Fridman,and K.H.Johansson,“Dynamic quantization of uncertain linear networked control systems,”Automatica,vol.59,pp.248-255,Sep.2015.

[26]J.Wang and H.Li,“Stabilization of a continuous linear system over channel with network-induced delay and communication constraints,”Eur.J.Contr.,vol.31,pp.72-78,Sep.2016.

[27]Y.He,Y.-E.Wang,and X.-M.Li,“Quadratic stabilization for linear time-delay systems with a logarithmic quantizer,”Neurocomputing,vol.173,pp.1995-2000,Jan.2016.

[28]K.Wen,Z.Y.Geng,Z.Y.Zhang,and L.J.Zhang,“A new model of networked control systems in robust control framework,”Asian J.Contr.,vol.18,no.1,pp.390-399,Jan.2016.

[29]M.Nagai,M.Shino,and F.Gao,“Study on integrated control of active front steer angle and direct yaw moment,”JSAE Rev.,vol.23,no.3,pp.309-315,Jul.2002.

[30]F.Rasool,D.Huang,and S.K.Nguang,“RobustH∞output feedback control of discrete-time networked systems with limited information,”Syst.Contr.Lett.,vol.60,pp.845-853,Oct.2011.

[31]L.H.Xie,“Output feedbackH∞control of systems with parameter uncertainty,”Int.J.Contr.,vol.63,no.4,pp.741-750,Jan.1996.

[32]L.El Ghaoui,F.Oustry,and M.AitRami,“A cone complementarity linearization algorithm for static output-feedback and related problems,”IEEE Trans.Automat.Contr.,vol.42,no.8,pp.1171-1176,Aug.1997.