电动汽车混沌振动信号的小波神经网络预测

牛治东， 吴光强,2

(1. 同济大学 汽车学院， 上海 201804； 2.东京大学 生产技术研究所， 东京 153-8505)

预测是在掌握相关信息的基础上，运用相关领域的定性或定量的方法，研究事物未来发展及其运行规律，并对其各主要素的变动趋势做出估计描述与分析的一门学科[1]。混沌理论表明，即使系统初始状态条件的细微差别，系统演化也可能导致显著差异，因而对混沌系统的长期演化结果是不可预测的，但由于混沌运动是由确定系统的内在特性所引起的，短期行为又是完全确定的，即可预测[2]。

对混沌时间序列预测方面的研究，文献[3]对时间序列观测数据进行处理，计算出最大Lyapunov指数，得到最大可预报时间尺度，并建立人工神经网络预测预报混沌时间序列的模型，验证了该预测方法。文献[4]讨论了神经网络预测在非线性动力学系统建模中的作用，利用反向传播学习规则去训练神经网络和预测误差，研究表明基于神经网络的时间序列预测能反应系统的动力学性能，并利用最大Lyapunov指数和相关维等作为一个近似工具验证预测模型的准确性。文献[5]提出了利用径向基函数(RBF)神经网络预测模型对混沌时间序列相空间重构的两个关键参数-延迟时间和嵌入维数进行联合估计的方法，并以Lorenz系统为例进行数值分析，验证了方法的有效性。文献[6]提出了基于混沌径向基神经网络的汽油机瞬态工况油膜参数预测模型，证明了汽油机油路系统时间序列具有非线性混沌特性，对试验测定的数据进行相空间重构，利用RBF神经网络对重构后的数据进行训练和预测，并利用数值方法验证了混沌RBF神经网络模型具有较强的非线性预测能力。

本文基于某款电动汽车实车试验测得的时间序列进行分析，研究振动信号的混沌特性，并采用小波神经网络预测模型对混沌时间序列进行了预测。首先，对电动汽车实车试验数据进行提取，确定作为分析对象的时间序列范围。其次，利用庞加莱截面、功率谱和最大Lyapunov指数等方法发现了电池底部中心和右前轮心垂向加速度时间序列具有混沌特性。最后，对右前轮心垂向混沌时间序列进行相空间重构，利用小波神经网络预测模型对重构后的相空间进行训练和预测，发现利用小波神经网络预测模型对混沌时间序列进行预测时，具有较强的预测能力。

1 混沌时间序列分析基础

混沌运动具有三个明显的特征[7]：①对初始条件的极端敏感依懒性；②非周期性表明混沌的非线性和无序性；③存在奇异吸引子。

对混沌时间序列分析的主要判别方法有：庞加莱截面；Lyapunov指数；功率谱；分形和分维；奇异吸引子；熵；关联维等。

混沌时间序列的预测方法主要有：全域法、局域法、加权零阶局域法、加权一阶局域法、基于李雅普诺夫指数的预测方法、小波分析、神经网络和小波神经网络方法等[8]。其中，小波神经网络方法适用于处理复杂系统的非线性关系，对数据量的要求不高。小波神经网络方法结合了小波变换良好的时频局域化性质、聚焦特性，神经网络的自学习、自适应、容错性，因而具有较强的逼近和容错能力。因为混沌时间序列具有对初值的敏感依赖性和非线性等特性，且通过试验采集到的数据量有限，为了对时间序列达到较好的预测效果，所以，本文采用小波神经网络方法对混沌时间序列进行预测。

本文利用功率谱、庞加莱截面和最大Lyapunov指数来分析时间序列的混沌特性。并用小波神经网络预测模型对混沌时间序列进行预测。下面分别介绍利用Wolf方法计算最大Lyapunov指数和小波神经网络预测模型的相关知识。

1.1 Wolf方法计算最大Lyapunov指数

为了得到最大Lyapunov指数，1985年，Wolf等[9]提出了轨迹跟踪法，随后Rosenstein等[10]进行了改进。从单变量的时间序列提取Lyapunov指数的方法是基于时间序列的重构相空间。Wolf等提出了直接基于相轨线、相平面、相体积等的演化来估计Lyapunov指数。这类方法统称为Wolf方法。

设混沌时间序列x1，x2，…，xn，…，嵌入维数m，时间延迟τ，则重构相空间

Y(ti)=(x(ti),x(ti+τ)),…,x(ti+(m-1)τ)

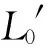
继续上述的过程，直至Y(t)到达时间序列的终点N，这时追踪演化过程总的迭代次数为M，则最大的Lyapunov指数为

(1)

1.2 混沌时间序列的小波神经网络预测

小波神经网络是一种以BP神经网络拓扑结构为基础，把小波基函数作为隐含层节点的传递函数，信号前向传播同时误差反向传播的神经网络。小波神经网络预测的一般计算流程如图1所示。

图1 小波神经网络预测的一般流程 Fig.1 Wavelet neural network prediction general process

小波神经网络的权值参数修正采用梯度修正法，修正输入输出层权值和小波基函数的参数，从而使小波神经网络预测输出不断逼近期望输出[11]。

小波神经网络的拓扑结构如图2所示。

图2 小波神经网络拓扑结构 Fig.2 Wavelet neural network topological structure

图2中，X1,X2, …,XK是小波神经网络的输入参数，Y1小波神经网络的预测输出，ωij和ωj为小波神经网络的权值。

(2)

式中：h(j)为隐含层第j个节点输出值；ωij为输入层与输出层之间的连接权值；hj为小波基函数；bj为小波基函数hj的平移因子；aj为小波基函数hj的伸缩因子；l为隐含层节点数。

输出层的计算公式为

(3)

本文采用的小波基函数为Morlet母小波基函数，数学公式为

y=cos(1.75x)e-x2/2

(4)

2 电动汽车试验

实车在中等比利时路面上行驶时采集信号，采集右前轮心垂向、电池底部中心三向加速度信号。如图3、图4所示，中等比利时路面及右前轮垂向和电池底部中心三向加速度传感器安装位置。采样频率512 Hz，对信号进行采集时，车速稳定在40 km/h。

图3 试验用中等比利时路面 Fig.3 Test of medium-Belgian pavement

图4 右前轮心垂向与电池底部中心三向加速度传感器 Fig.4 Vertical of right front wheel center and three direction of battery bottom center acceleration sensor

因实车试验数据量较大，本文选取右前轮心垂向和电池底部中心垂向的振动加速度信号进行分析。因试验条件限值，试验路面不连续，试验时，试验前几秒，车速不稳定，所以选取15～45 s的数据进行处理和分析。如图5、6所示。

图5 右前轮心垂向加速度信号 Fig.5 Vertical acceleration signal of right front wheel

图6 电池底部中心垂向加速度信号 Fig.6 Vertical acceleration signal of battery bottom center

3 混沌时间序列的特性分析

3.1 时频分析

实车试验采集到的信号为非平稳信号，对信号进行时频分析时，采用短时傅里叶变换。如图7、8所示。发现两个信号的能量主要集中在10 Hz附近。

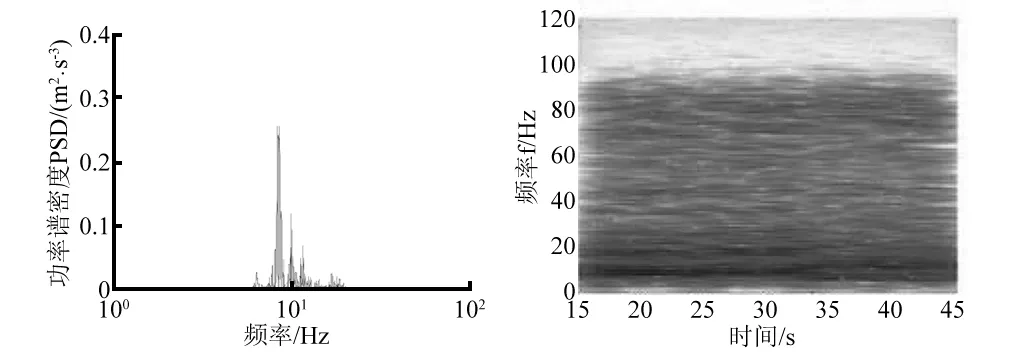
图7 右前轮心垂向功率谱密度与时频图 Fig.7 Power spectrum density and time frequency diagram of vertical right front wheel

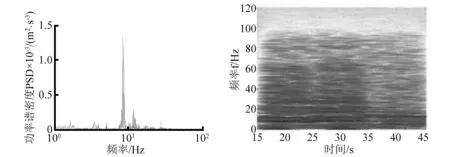
图8 电池底部中心垂向功率谱密度与时频图 Fig.8 Power spectrum density and time frequency diagram of vertical battery bottom center

3.2 三维相图与庞加莱截面

两个振动信号的三维相图和庞加莱截面，如图9、10所示。从图9、10中可以看出，右前轮心垂向与电池底部中心垂向的相图为一些杂乱无章的曲线，庞加莱截面均为一些成片的密集的点集。

图9 右前轮心垂向相图与庞加莱截面 Fig.9 Phase diagram and Poincare sections of vertical right front wheel

图10 电池底部中心垂向相图与庞加莱截面 Fig.10 Phase diagram and Poincare sections of vertical battery bottom center

3.3 最大Lyapunov指数

首先利用互信息量法计算延迟时间，Cao法计算嵌入维。选择合适的延迟时间及最小嵌入维，利用Wolf方法计算最大Lyapunov指数。

计算时间延迟的主要方法有自相关法、平均位移法和互信息量法等。其中，互信息量法[12]是估计重构相空间延迟的一种有效方法，它包含了时间序列的非线性特征。计算时间延迟，如图11、12所示。

图11 右前轮心垂向时间序列延迟时间 Fig.11 Time delay of vertical right front wheel center

图12 电池底部中心垂向时间序列延迟时间 Fig.12 Time delay of vertical battery bottom center

计算嵌入维的主要方法有：C-C方法、虚假邻点法和Cao法等。利用Cao法[13]计算最小嵌入维数，只需知道延迟时间和较小的数据量就能求得嵌入维数，并且能有效区分随机信号和确定信号。本文选用Cao法计算嵌入维，如图13、14所示。

图13 右前轮心垂向时间序列嵌入维 Fig.13 Embedding dimension of vertical right front wheel

图14 电池底部中心垂向时间序列嵌入维 Fig.14 Embedding dimension of vertical battery bottom

根据图11、图12选择两个信号的延迟时间为：10、12。根据图13、图14选择两个信号的最小嵌入维：11、9。根据选择的延迟时间和最小嵌入维，利用Wolf方法计算右前轮心垂向和电池底部中心垂向振动加速度信号时间序列的最大李雅普诺夫指数分别为：0.000 073 087、0.001 3。表明两处信号的时间序列具有混沌动力学特性。

4 混沌时间序列的小波神经网络预测

采用小波神经网络预测模型对右前轮心垂向加速度混沌时间序列进行预测。根据右前轮心垂向加速度时间序列的延迟时间和嵌入维数，进行相空间重构。相空间重构是一种基于有限的实测数据进行重构吸引子，从而进行系统动力学研究的方法。本文对一维时间序列进行相空间重构，得到多维相空间信号，利用重构后的相空间对混沌时间序列进行预测。目前，神经网络输入层节点数的确定一般采用试凑法，即不断改变输入层节点数，直到达到模型精度要求，但该方法这样带来的不利因素是计算量的增大，而且不利于建立动态的预测模型。有研究表明：输入层的个数为混沌时间序列的重构相空间的饱和嵌入维数为最佳。

本文选取35～43 s之间的振动加速度时间序列进行分析。右前轮心垂向振动加速度时间序列如图15所示。

图15 右前轮心垂涎振动加速度 Fig.15 Acceleration of vertical right front wheel

在图15中，为一维时间序列，时间共8 s，4 096个数据样本点。选取前7 s，共3 584个数据点作为训练数据，后1 s，共512个数据点作为测试数据，以验证小波神经网络预测模型的预测效果。小波神经网络预测模型的输入层节点数等于右前轮心垂向混沌时间序列的最小嵌入维数。预测结果如图16所示，预测误差如图17所示。可以看出，利用小波神网络预测模型对混沌时间序列具有较高的预测能力。

图16 小波神经网络预测结果 Fig.16 Prediction results of wavelet neural network

图17 小波神经网络的预测误差 Fig.17 Prediction error of wavelet neural network

5 结 论

(1) 电动汽车在中等比利时路面进行实车试验，对试验数据进行提取，确定了作为分析对象的时间序列范围。

(2) 对信号进行了时频分析，并利用庞加莱截面、三维相图和最大Lyapunov指数等数值分析方法对加速度信号进行分析，发现了电池底部中心垂向和右前轮心垂向加速度时间序列具有混沌特性。

(3) 对右前轮心垂向加速度混沌时间序列进行相空间重构，利用小波神经网络对重构后的数据进行训练和预测。结果发现，利用小波神经网络预测模型对混沌时间序列进行预测时，具有较强的预测能力。

[ 1 ] 姜爱萍. 混沌时间序列的小波神经网络预测方法及其优化研究[M]. 上海：上海大学出版社, 2013.

[ 2 ] 韩敏. 混沌时间序列预测理论与方法[M]. 北京：中国水

利水电出版社, 2007.

[ 3 ] 许传华, 任青文, 房定旺. 基于神经网络的混沌时间序列预测[J]. 水文地质工程地质, 2003, 30: 30-32.

XU Chuanhua, REN Qingwen, FANG Dingwang. Prediction of chaotic time series based on neural network [J]. Hydrogeology & Engineering Geology, 2003, 30: 30-32.

[ 4 ] PRINCIPE J C, RATHIE A, KUO J M. Prediction of chaotic time series with neural networks and the issue of dynamic modeling [J]. International Journal of Bifurcation & Chaos, 2011, 2(4): 989-996.

[ 5 ] 陈帝伊, 柳烨, 马孝义. 基于径向基函数神经网络的混沌时间序列相空间重构双参数联合估计[J]. 物理学报, 2012, 61(10): 22-31.

CHEN Diyi, LIU Ye, MA Xiaoyi. Parameter joint estimation of phase space reconstruction in chaotic time series based on radial basis function neural networks [J]. Acta Phys. Sin, 2012, 61(10): 22-31.

[ 6 ] 徐东辉, 李岳林, 解福泉. 汽油机瞬态工况油膜参数的混沌径向基神经网络预测模型研究[J]. 汽车工程, 2015: 353-358.

XU Donghui, LI Yuelin, XIE Fuquan. A research on the prediction model for the fuel-film parameter of gasoline engine in transient conditions based on chaotic RBF neural network [J]. Automotive Engineering, 2015: 353-358.

[ 7 ] 黄润生. 混沌及其应用[M]. 武汉：武汉大学出版社, 2000.

[ 8 ] 吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉：武汉大学出版社, 2002.

[ 9 ] WOLF A, SWIFT J B, SWINNEY H L, et al. Determining lyapunov exponents from a time series [J]. Physica D Nonlinear Phenomena, 1985, 16(3): 285-317.

[10] ROSENSTEIN M T, COLLINS J J, LUCA C J D. A practical method for calculating largest Lyapunov exponents from small data sets [J]. Physica D-nonlinear Phenomena, 1993, 65(93): 117-134.

[11] 王小川. MATLAB神经网络43个案例分析[M]. 北京：北京航空航天大学出版社, 2013.

[12] 张菁, 樊养余, 李慧敏, 等. 相空间重构中延迟时间选取的新算法[J]. 计算物理, 2011, 28(3): 469-474.

ZHANG Jing, FAN Yangyu, LI Huimin, et al. An improved alogorithm for choosing delay time in phase space reconstruction [J]. Chinese Journal of Computational Physics, 2011, 28(3): 469-474.

[13] CAO Liangyue. Practical method for determining the minimum embedding dimension of a scalar time series [J]. Physica D, 1997, 110: 43-50.