剃齿啮合的接触特性分析及中凹误差形成机理研究

蔡安江， 刘 磊， 李 玲， 张 华， 杨选文， 郑 涛

(1. 西安建筑科技大学 机电工程学院，西安 710055； 2. 陕西法士特齿轮有限责任公司，西安 710077； 3. 浙江省农业机械研究院，浙江 金华 321017)

剃齿齿形中凹误差的存在是齿轮传动产生振动、噪声的主要因素之一，严重影响齿轮使用寿命和传动性能。剃齿过程为复杂的交错轴空间不连续曲面啮合，且伴随着工艺系统各种因素所产生的综合误差，使得齿面成形过程本身复杂化，因此中凹误差已成为世界性的难题[1]。

国内外学者普遍认为中凹误差的产生主要是因为节圆附近啮合接触点数变少，左右啮合线接触不平衡致使该区域产生受力冲击，导致剃齿刀切削深度增加，并伴有随机误差复映，从而形成0.01～0.03 mm的中部凹陷。因此，剃齿啮合的接触特性成为解决中凹误差的重点研究对象。Litvin等[2]提出螺旋锥齿轮齿面承载接触分析技术(LTCA)是研究齿轮接触力学性能的核心技术，其在齿面接触分析(TCA)技术基础上引入边缘接触理论，较好的克服了TCA技术的不足。但是在LTCA 分析过程中，若有2个以上的齿轮啮合时，啮合齿面压力分配及齿面变形大小等问题无法得到解决，需要结合材料力学的莫尔能量法、弹性力学、有限元柔度矩阵法等进一步求解。唐进元等[3]以多体系统误差建模理论为基础提出齿面误差接触分析(ETCA)，并以SGM 法加工锥齿轮为例，得到机床运动误差和安装误差对齿面加工质量影响的定量关系，比较TCA技术，表明ETCA的分析结果对指导加工更为合理。Moriwaki等[4-5]基于弹性理论建立一种新的随机切削模型，预测在精加工后剃齿刀的切削效果，并模拟了剃齿加工过程。Zhang等[6]建立了包含齿轮制造误差、齿形表面误差以及修形影响的交错轴啮合接触模型，分析其啮合情况与载荷分布，验证了小啮合角剃齿的良好效果。Chen等[7]建立螺旋齿轮和双鼓形齿轮组啮合模型，利用弹性理论和有限元法分析螺旋齿轮的接触应力与弯曲应力，验证了两种方法的一致性。但在剃削过程中，齿面弹塑性变形并存，研究剃齿齿形中凹误差需同时考虑弹塑性变形对齿面加工的影响。

上述针对齿面接触的研究方法为解决中凹误差问题拓宽了研究思路。通过计算啮合接触点法向作用力、接触应力和变形量分析接触特性，以接触应力为量纲划分齿廓的弹塑性变形区域，并确定不同载荷作用下的弹性、弹塑性和塑性变形区域，明确各变形阶段所产生齿形中凹误差的主要根源，从而为研究中凹误差形成机理提供理论依据。并应用有限元法及剃齿试验与理论计算分析进行对比，验证其正确性。

1 构建剃齿啮合分析模型

为得到剃齿啮合过程中法向作用力Fn和接触位置的应力σH及弹性变形压缩量δe，需确定齿廓上每一瞬时的接触点数与位置，而啮合方程和齿面方程则是获取接触点位置的前提。为了解决这几个问题，剃齿啮合分析模型应包括几何模型、数学模型和力学模型。

1.1 几何模型

剃齿啮合中，由于剃齿刀齿面的容屑槽和切削刃的存在，使其在工件齿面上的接触线为间断的空间曲线，这使得啮合接触问题复杂化，根据文献[8]可将剃齿过程简化为一对斜-直齿轮作交错轴空间啮合运动。由于绝大部分中凹误差都是发生在剃齿啮合重合度小于2的刀齿对，选取剃齿刀和工件齿轮参数如表1所示，推导出相应的剃齿啮合参数，其中重合度为1.401。建立如图1所示的三维几何模型，为方便后述数学模型推导，建立相应坐标系。

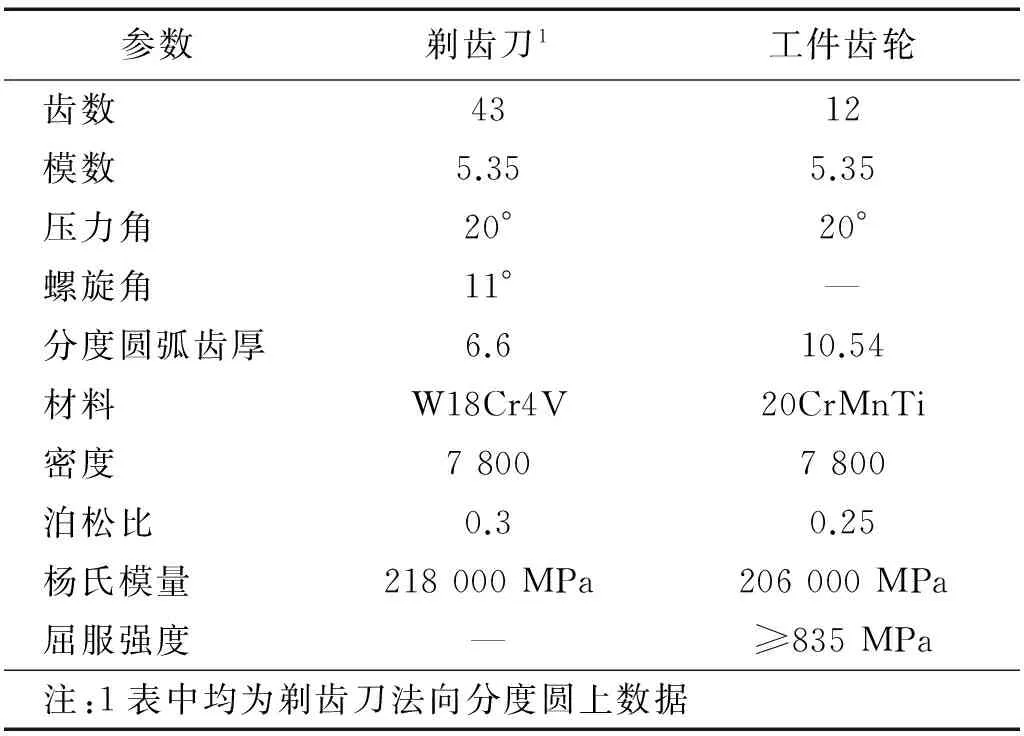
表1 剃齿刀和工件齿轮参数Tab.1 Prametters of shaving cutter and work gear

图1 剃齿啮合几何模型 Fig.1 Geometric model of shaving

1.2 数学模型

剃齿加工为双自由度啮合过程，根据啮合原理和如图1参数，用坐标系S1(O1-x1y1z1)来表示啮合方程式为：

(1)

啮合方程中只含有两个独立参数，角速度ω1和轴向运动速度v02，所以式(1)可整理简化成两个条件式

U1cosφ1-V1sinφ1=W1

(2)

U2cosφ2-V2sinφ2=W2

(3)

式(2)、式(3)可知，两个条件式都是角速度φ1与齿面参数(u,θ)的关系式，取一定的φ1角，可以映射出多个(u,θ)值。它的几何意义为当选定一个转角值时，有一系列剃齿刀齿面Σ(1)上的点同时满足啮合，即齿面上此时有一条啮合接触线。若需要同时满足式(2)和式(3)，则只有一对(u,θ)解，即任一瞬时在剃齿刀齿面Σ(1)上只有一个接触交点[9]。显然，若两个条件式的形式相同或者对应成比例，可视为剃齿啮合点接触向线接触蜕变，即满足如下蜕变条件式：

(4)

把式(1)、式(2)和式(3)整理代入式(4)，两个方程可求出唯一解，化简后的形式：

(5)

式中：p1为剃齿刀螺旋参数。

为了获得剃齿刀与工件齿轮线接触啮合，需保证传动比i21与i″之比等于剃齿刀螺旋面Σ(1)的螺旋参数p1与轴交角的余弦之比。在实际操作中，需要按照一定的要求来调整剃齿机，其中传动比为i21=z1/z2，而传动比i″则由差动机构实现，其意义为当剃齿刀相对工件齿轮移动一个导程2πp1，要保证工件齿轮的附加转角为

(6)

工程实践中，三自由度齿轮啮合方程可以简化成三个条件式，其蜕变成两个条件式之后就是对角滚齿的理论基础。联立式(2)、式(5)，得啮合关系式

(7)

把式(7)代回式(2)或式(3)，可以得到关于θ的超越方程，由牛顿迭代算法计算结果为发散。若画出相应图形，会有无数个交点，该结果与点接触蜕变为线

接触的观察结果相一致。显然，蜕变后啮合面方程以及工件齿轮齿面Σ(2)方程可利用坐标转换得出，这里不再赘述。

1.3 力学模型及LTCA

剃齿加工实际上为无侧隙啮合挤压切削过程，以加工工件齿轮右齿面Σ(2)为例，当剃齿刀左(右)齿面为切削侧时，剃齿刀右(左)齿面仅作挤压抛光和平衡力矩的作用，可知一个完整的剃削过程中工件齿轮左右齿面受力对称，故选取工件齿轮右齿廓作为研究对象。根据上述数学模型，建立剃齿啮合的力学模型，如图2所示，并对模型进行齿面载荷接触分析(LTCA)[10]。图2中：L1,L2,L3,L4为各接触点到动坐标系S2轴y2的距离，K1,K2,K3,K4为有效啮合线的各极限接触点，F1,F2,F3,F4为各法向作用力，Fr为给定径向力。

求解啮合过程中的接触变形，需推导出接触点的法向作用力。当重合度小于2的刀齿啮合时，有三种啮合状态交替变化。齿面上法向作用力随啮合状态变化而变化，现对图2三种啮合状态进行详细的力学分析。三点接触与两点接触的受力为简单的静力学分析，此处不再赘述。当四点接触(见图2(c))时，系统保持平衡状态有四个力F1,F2,F3,F4未知，通过力和转矩的平衡只能得到三个方程式，需要额外添加一个协调方程，其含义为左右啮合线的接触变形量之和相等。

(8)

式中：b为各接触点接触椭圆的长轴长;F为各接触点的法向作用力。

图2 剃齿啮合状态及力学模型 Fig.2 Meshing state in shaving andmechanical model

解出三种啮合状态下的法向作用力后，可求得相应的弹性变形压缩量δe[11]。

(9)

考虑齿形中凹误差出现在工件齿轮齿面节圆附近，而齿面接触点所受的弯曲应力要比接触应力小得多，故只对齿轮进行接触分析。根据AGMA标准给出斜齿轮齿面接触应力计算公式为[12]

(10)

式中： 实际载荷系数KH=KAKVKHαKHβ。

剃齿过程的剃削力主要由径向进给量确定[13]，不同的径向力会对剃齿造成不同的剃削变形。径向力的值一般在700～2 000 N之间，选取四种不同径向力700 N，1 100 N，1 500 N和2 000 N 作用下，利用上述方法对右齿廓进行啮合接触分析，由静力学分析求出每种状态下的法向作用力，然后由式(9)、式(10) 确定右齿廓任意曲率半径的变形量及接触应力值。分别得到不同载荷条件下的啮合接触特性曲线如图3所示。

图3表明，在齿廓有效剃削段的左右啮合线上，刀齿接触点数变化为4(AB段)-3(BC段)-2(CD段)-3(DE段)-4(EF段)-3(FG段)，其中两点接触段(CD)作用时间最长。在不同载荷径向力下，工件齿轮齿面接触应力和变形量变化趋势大体一致，其大小随径向力的增大而增大，实际上由于系统随机误差的存在，变形量曲线变化并不会跟随接触应力的变化。此外，齿根部EG段所受的应力较之齿顶部AC段更大，所形成的变形量也更大，造成相应的齿形误差也越大，这与工程实践中观察的结果相一致。三点接触段BC的应力和变形量较之四点接触段AB下降，其原因在于AB段对应图2(b)中的F2，而DE段和FG段对应F1和F3，径向力Fr从四点接触向三点接触变化时，大部分作用力由F1和F3平衡。两点接触段CD接触齿对数减小，重合度减小，法向作用力增大，故接触应力和变形量也随之急剧增大。节圆附近的三点接触段DE出现了应力和变形量的峰值，其值与两点接触的CD段大致相等，但在该区域内为三点接触，左右齿面受力不平衡，当径向力足够大时，该区域会比CD段更容易出现塑性变形。随着剃齿低周啮合，塑性变形量不断累积，齿形误差复映，DE段最终会在齿廓上表现为明显的中凹误差现象。

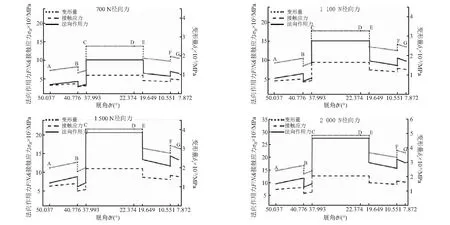
图3 不同径向力下剃齿啮合接触特性曲线 Fig.3 Meshing contact characteristic curve under different loading condition in shaving

2 弹塑性变形分区

研究剃齿加工过程中两齿面间的弹性极限，利用齿面开始进入完全塑性变形阶段时的临界载荷与齿面完全弹性变形时的临界载荷之间的关系，确定两齿面开始进入塑性变形阶段时的临界应力值，以接触应力为量纲来划分齿廓任意曲率半径的弹塑性变形区域。

2.1 弹塑性分析

在剃齿加工初期，剃齿刀和工件齿轮啮合接触点的法向作用力较小，其接触应力在弹性范围内，加工完成后弹性变形会因作用力的消失而恢复。随着剃削过程的进行，径向力会随着进给量的增大而增大，接触点的法向作用力也会随之变大。当法向力足够大时，接触点所受的应力σ≥σs时，刀齿间的接触应力超过弹性极限，开始进入屈服阶段。由于弹性强度的准确测量极为困难，通常以产生0.005%～0.05% 的残余变形所对应的应力作为弹性极限，其数值上与屈服强度非常接近，在工程应用中常不做区分，故可选取材料的屈服极限作为材料从弹性变形进入塑性变形的理论判据。已知工件齿轮材料的屈服强度为≥835 MPa，为了保证工程安全性，这里取最小值835 MPa作为判断剃齿过程中是否发生塑性变形的理论应力数值。如图3所示，当径向力Fr=1 500 N时，齿廓两点接触段CD、三点接触段DE和局部四点接触段EF 的应力达到835 MPa以上，认为这些区域将出现塑性变形。

2.2 不同径向力下弹塑性变形分区

随着剃削低周运动，塑性变形因不能恢复而误差复映在齿面上，最终会在剃齿加工完成后形成齿面误差，可见塑性变形区域的存在会直接引起齿形中凹误差。在齿廓上精确划分出弹塑性变形区域对消除中凹误差影响有着重要的指导意义。

工件齿轮在上述力学模型中作为理想弹性体来分析，所计算的变形量也按照弹性阶段处理，考虑到晶体内部的位错运动，连续的法向力会使该接触点处出现屈服现象，显然理论计算的变形量与实际的塑性变形量存在着较大的误差，故采用接触应力作为量纲来对齿廓的接触区域进行弹塑性区域的划分。不同径向力下划分的弹塑性变形区域，如图4所示。

图4 接触应力为量纲的弹塑性变形区分 Fig.4 Elastoplastic deformation region by contact stress

图4可知，在不同径向力的作用下，两点区域的CD段和节圆附近的三点区域(DE段)在剃齿过程中最先出现塑性变形，且随着径向力的增大塑性变形区域逐渐扩大到齿根部位的三点接触区域(FG段)和四点接触区域(EF段)，可见径向力增大会加剧中凹误差的出现。而齿面中凹误差最容易在节圆附近累积，若能优化剃齿参数来减小该区域的受力，就能缩小塑性变形区域，进而从根本上减小中凹误差量。

3 有限元仿真及理论计算对比

3.1 有限元分析前处理

剃齿刀和齿轮的几何形状、边界条件和载荷均符合旋转周期结构的要求，即模型的位移关于中心轴呈周期性对称布置，可选取局部模型来代替整体模型。Celik[14]验证比较了整体模型和局部模型的应力应变结果，两者的计算误差仅在2%以内，故局部模型代替整体模型可满足工程应用。当重合度小于2的刀齿啮合时，至多有5个齿参与啮合，同时为避免边缘刚体耦合约束对计算结果的影响，对刀齿各截取五个轮齿进行分析。

3.2 不同径向力下的接触应力及弹塑性变形分区

选取与力学模型一致的四种径向力，对其分别进行仿真及数据处理，接触应力仿真结果如图5所示。在图3中每一啮合状态的变化都会引起接触特性的突变现象，而图5中，在实际剃削中会存在一个过渡区，使传动平稳进行。

图5 不同径向力下接触应力曲线及齿廓弹塑性变形分区 Fig.5 Contact stress curve under different loading and partition of elastoplastic deformation

图5表明，螺旋剃齿刀的接触状态因载荷条件的不同而不同，弹塑性区域也会随之变化，载荷越大塑性区域也越大。当径向力Fr=700 N时，两种方法计算的最大误差为9.77%。其原因为：剃削加工初始状态时，切削力小，剃前齿面误差、安装误差等其他系统误差影响大，针对齿面接触特性，这些误差无法应用AGMA标准来计算。而工件齿轮进入有效剃削阶段，剃削力增大，齿面上开始出现塑性变形，两种方法计算的误差变大，且随径向力增大而增大，误差分别为12.63%、15.05% 和19.18%，其偏差原因有很多：当径向力增大时，刀齿啮合的重合度改变，啮合状态发生变化，故法向作用力和接触应力也随之变化；剃齿过程中，工件齿轮循环次数在105以下，处于低周疲劳阶段，而根据AGMA标准计算的接触力结果不能很好的反映其疲劳误差复映等。对比理论计算结果，两种方法划分的弹塑性区域及发展规律大体一致，且FEM法计算划分的塑性变形区域比按AGMA 标准计算划分的区域较大。其误差主要是因为Abaqus有限元软件应用准静态动态来仿真，故系统动态质量导致轮齿仿真变形会大于理论计算变形[15]。根据LTCA分析结果，三点啮合段DE是塑性变形最大的区域，而仿真结果在该段齿廓中并不是变形的峰值，只出现一个区域极大值，其原因是：DE段啮合到EF段，啮合状态变化较大，为保证有限元收敛，仿真过程中需要作用时间较长的过渡区来实现，而DE段转角仅为0.76°，过渡区使得三点接触应力作用时间太短，故只出现一个局部极大值。

4 剃齿试验对比与分析

不同径向力可由不同的剃削用量来确定，控制其他工艺参数不变，采用不同的径向进给量就可以得到大致的径向力大小[13]。选用YW4232剃齿机加载不同的进给量对同一工件齿轮参数进行试剃，再应用万能齿轮测量仪GM 3040a对剃后齿轮进行齿形齿向的检测。不同径向力的剃齿齿形图如图6所示。

图6 不同径向力的齿形试验图 Fig.6 Test diagram of gear profile with different loading

图6表明，该剃齿参数下，工件齿轮节圆附近均出现不同程度地凹陷，且随着径向力增大，齿形中凹误差量增大，与图3接触特性曲线变化一致，证明了该理论接触特性曲线分析齿形中凹误差的正确性。对比图3、图5可知，其理论计算及有限元法接触特性曲线和图6中齿形图变化轨迹基本一致，但是在齿形图上存在凸出区域，即实际齿形凸出于标准渐开线，而AGMA标准计算及FEM计算只存在凹陷误差。其原因为：理论计算仅仅是在标准渐开线上进行弹塑性分析，故只会形成相应凹陷，而实际工况复杂，剃前齿形误差的存在及让刀现象使接触区域周围形成挤压而产生凸出变形。图6(a),图6(d)的齿形较之图6(b),图6(c)齿形存在局部波动，原因如下：当径向进给量过小，导致刀齿不能切入金属层，只能挤压金属表面，不能纠正剃齿误差；进给量过大则会过度切除金属，从而破坏原有的精度，故导致齿形的波动。此外，随着径向力的增大，其齿形误差曲线变化一致，且齿形误差先随之变大，如图6(a),图6(b),图6(c)，当径向力足够大时，齿形误差不再单调变大，而是出现振荡，如图6(c),图6(d)所示，其原因为：工件齿轮齿形误差会影响剃齿传动性能，传动不平稳又会进一步影响其接触特性，导致齿形误差变化不一致。

5 结 论

针对剃齿啮合的力学特性，利用LTCA技术分析剃齿啮合接触特性，并依据弹塑性理论对齿廓任意曲率半径划分变形区域，通过有限元法和剃齿试验来验证理论研究，其主要结论如下：

(1) 推导了齿轮双自由度啮合时，啮合接触由点接触向线接触蜕变的条件i21/i″=p1/cosΣ，使啮合受力更加均衡，传动更加平稳，此蜕变公式可以推广到任意两轴齿轮运动。

(2) 通过LTCA技术对剃齿啮合进行接触状态分析，给出了不同径向力Fr条件下的剃齿啮合接触特性曲线。结果表明：随着径向力的增大，接触应力及变形量随之增大；齿根部接触应力和变形均比齿顶部大；接触应力和变形量的峰值出现在节圆附近，表明这些区域最容易出现中凹现象。

(3) 利用有限元法分析了不同径向力下齿面接触状态，计算结果与AGMA计算比较可知，在剃齿加工初期径向力(700 N)和切削力较小时，两种方法计算的误差达9.77%。而当径向力逐渐增大偏差呈非线性增大，两者计算结果最大偏差分别为12.63%(1 100 N)、15.05%(1 500 N)和19.18%(2 000 N)。

(4) 根据AGMA标准和FEM法计算的接触应力值，分别对齿廓进行弹塑性区域划分，比较结果一致，塑性变形区域随径向力增大而增大，且从节圆附近向齿顶和齿根扩展。仿真结果表明弹塑性变形区域划分有效。

(5) 剃齿试验表明，在不同径向力条件下均出现不同程度的中凹误差现象，并随着径向力的增大而增大，验证了剃齿啮合接触特性分析齿形中凹误差的正确性。且剃齿啮合间的传动特性会直接影响到齿面成形质量。

[ 1 ] TISZA M. Numerical modeling and simulation in sheetmetal forming [J]. Journal of Materials Processing Technology, 2004, 151(1/2/3): 58-62.

[ 2 ] LITVIN F L, LU J. Computerized design and generation of double circular-archelical gears with low transmission errors [J]. Computer Methods In Applied Mechanics And Engineering, 1995, 127: 57-86.

[ 3 ] 唐进元, 卢延峰, 周超. 有误差的螺旋锥齿轮传动接触分析[J]. 机械工程学报, 2008, 44(7): 16-23.

TANG Jinyuan, LU Yanfeng, ZHOU Chao. Error tooth contact analysis of spiral bevel gears transmission [J]. Journal of Mechanical Engineering, 2008, 44(7): 16-23.

[ 4 ] MORIWAKI I, FUJITA M. Effect of cutter performance on finished tooth form in gear shaving [J]. Journal of Mechanical Design, 1994, 116(3): 701-705.

[ 5 ] ICHIRO M, MASAKATSU F, TAKASHI O, et al. Numerical analysis of tooth forms of shaved gears [J]. JSME, International Journal Series Ⅲ, 1990, 33(7): 608-613.

[ 6 ] ZHANG Yu, YAN Hongzhi, ZENG Tao, et al. Tooth surface geometry optimization of spiral bevel and hypoid gears generated by duplex helical method with circular profile blade [J]. J Cent South Univ, 2016, 23: 544-554.

[ 7 ] CHEN Y C, TSAY C B. Stress analysis of a helical gear set with localized bearing contact[J]. Finite Elements in Analysis and Design, 2002:707-723.

[ 8 ] 左俊. 剃齿加工仿真及齿形中凹误差机理研究 [D]. 重庆: 重庆大学, 2012.

[ 9 ] 吴序堂. 齿轮啮合原理[M]. 西安: 西安交通大学出版社, 2009.

[10] JIANG Jinke, FANG Zongde. Design and analysis of modified cylindrical gears with a higher-order transmission error [J]. Mechanism and Machine Theory, 2015, 88: 141-152.

[11] KIYOHIKO U. Deflections and moments due to a concentrated load on a rack-shaped cantilever plate vvith finite width for gears [J]. Bulletin of the JSME, 1972, 15(79): 116-130.

[12] JOHNSON K L. Contact mechanics [M]. Combridge: Combridge University Press, 1985.

[13] 吕明, 冯肇锡, 徐璞. 剃齿切削力的研究[J]. 太原工业大学学报, 1987(4): 61-73.

LÜ Ming, FENG Zhaoxi, XU Pu. The research on shaving force [J]. Journal of Taiyuan University of Technology, 1987(4): 61-73.

[14] CELIK M. Comparison of three teeth and whole models in gear analysis [J]. Mechanism and Machine Theory, 1999(34): 1227-1235.

[15] 王峰, 方宗德, 李声晋. 斜齿轮动力学建模中啮合刚度处理与对比验证[J]. 振动与冲击, 2014, 33(6): 13-17.

WANG Feng, FANG Zongde, LI Shengjin. Treatment and contrast verification of meshing stiffness in dynamic model of helical gear[J]. Journal of Vibration and Shock, 2014, 33(6): 13-17.

[16] FAKHER C, TAHAR F, MOHAMED H. Analytical modelling of spur gear tooth crack and influence on gear mesh stiffness [J]. European Journal of Mechanics A/Solids, 2009, 28: 461-468.

[17] 蔡安江, 张振军, 阮晓光. 基于剃齿修形的啮合角数值计算 [J]. 中国机械工程, 2013(10): 1327-1330.

CAI Anjing, ZHANG Zhenjun, RUAN Xiaoguang. Pressure angle values based on shaving modification terms [J]. China Mechanical Engineering, 2013(10): 1327-1330.