基于阻力和EEDI的船舶主尺度要素多学科设计优化
2018-04-30苏绍娟介推刘波
苏绍娟 介推 刘波

摘要:
为寻找高效节能船舶主尺度要素,以一艘多用途船作为研究对象,从多学科设计优化的角度入手,根据普鲁哈斯卡假设和三因次换算方法将船舶阻力参数化,采用等效能效指数将船舶能效设计指数(energy efficiency design index, EEDI)参数化,使其均为船舶主尺度要素函数。选用合适的多学科设计优化模型,运用第二代非支配排序遗传算法(second generation non-dominated sorting genetic algorithm, NSGA-II)得到优化的船舶主尺度要素。对原船进行船型变换,得到优化船。利用CFD进行数值模拟,验证优化船的阻力性能和EEDI优于原船的阻力性能和EEDI,达到优化的目的。
关键词:
船舶能效设计指数(EEDI); 船舶主尺度; 多学科设计优化; 阻力
中圖分类号: U661.1;U662
文献标志码: A
Multidisciplinary optimization design on ship principal dimensions
based on resistance and EEDI
SU Shaojuan1, JIE Tui1, LIU Bo2
(1. Naval Architecture and Ocean Engineering College, Dalian Maritime University, Dalian 116026, Liaoning, China;
2. Marine Departmnet, Dalian Shipping College, Dalian 116000, Liaoning, China)
Abstract:
To find the principal dimensions of high efficiency and energy saving ships, a multi-purpose ship is studied. From the perspective of the multidisciplinary optimization design, the ship resistance is parameterized according to Prohaska hypothesis and the three-dimensional conversion method, and the energy efficiency design index (EEDI) is parameterized using the equivalent efficiency index, which makes them to be the ship principal dimension functions. An appropriate multidisciplinary optimization design model is chosen. The second generation non-dominated sorting genetic algorithm (NSGA-II) is used to get the optimal ship principal dimensions. The original ship is converted into an optimal ship. The numerical simulation by CFD verifies that the resistance performance and EEDI of the optimal ship are superior to those of the original ship, thus the optimization is achieved.
Key words:
energy efficiency design index (EEDI); ship principal dimension; multidisciplinary optimization design; resistance
收稿日期: 2017-05-03
修回日期: 2017-11-22
基金项目: 国家自然科学基金(51609031);中央高校基本科研业务费专项基金(3132016346,3132017018);辽宁省教育厅科学研究一般项目(L2015067)
作者简介:
苏绍娟(1979—),女,辽宁葫芦岛人,副教授,博士,研究方向为数字化船舶设计制造,(E-mail)katie306@163.com
0 引 言
船舶主尺度要素优化是一个复杂的非线性优化问题,涉及的因素较多。长期以来,国内外专家学者对此做了大量的研究工作:金雁等[1]运用网格法和AHP将多目标转化为单目标进行船型主尺度论证;张宝吉等[2]以最小阻力为目标采用遗传算法进行船型优化设计;刘寅东等[3]应用AHP和1~9标度将定性分析与定量分析结合,解决船型优选排序问题;金雁等[4]采用蚁群算法进行船舶主尺度优化论证。上述研究有的考虑阻力等单一技术指标,有的考虑技术、经济等多个指标,均能有效地选择合理的船型主尺度要素,但很少从系统的角度考虑各指标间的内在联系。刘蔚[5]将7 000 m载人潜水器分解为若干个子系统,结合不同的多学科设计优化方法对其进行优化,取得了不错的成果。张恒等[6]基于船的水动力性能对船型进行了综合优化,并开发了船体型线多学科设计优化平台,实现了基于所需目标的船体型线自动优化过程。
本文以一艘多用途船作为研究对象,研究阻力性能和
船舶能效设计指数(energy efficiency design index, EEDI)及其相互作用关系,通过多学科设计优化设计理论,采用第二代非支配排序遗传算法(second generation non-dominated sorting genetic algorithm, NSGA-II)对该船的船型要素值寻优,从而实现寻找高效节能船型的目的。
1 阻力参数化
根据三因次换算方法[7],船模的总阻力因数为
Ctm=Cpvm+Cfm+Cwm=(1+k)Cfm+Cwm (1)
式中:1+k为形状因子;Cpvm,Cfm和Cwm分别为船模的黏压阻力因数、摩擦阻力因数和兴波阻力因数。
按照普鲁哈斯卡假设,通常弗劳德数Fr在0.1与0.2之间时,可近似认为Cwm与Fr的四次方呈线性关系,故将式(1)变换为
CtmCfm=1+k+bFr4Cfm (2)
k采用Granville提供的计算公式[8]计算:
k=-0.03+32.8C2b(Lpp/B)2B/T (3)
式中:Cb为方形系数;Lpp为垂线间长;B为型宽;T为设计吃水。
摩擦阻力因数用国际拖曳水池会议(ITTC)公式计算:
Cf=0.075(lg Re-2)2(4)
式中:雷诺数Re=vLwl/ν,其中v为航速,Lwl为水线间长,ν为水的运动黏性系数,取海水在20 ℃时的运动黏性系数。
在相同Fr的情况下,船模兴波阻力因数Cwm等于实船兴波阻力因数Cw,故实船总阻力因数为
Ct=(1+k)Cf+Cwm+ΔCf=
(1+k)(Cf-Cfm)+Ctm+ΔCf
(5)
ΔCf为粗糙度补贴因数,通常取0.4×10-3,也可用ITTC推荐的公式:
ΔCf=105ksLwl1/3-0.64×10-3 (6)
ks通常取1.5×10-4 m,因此实船总阻力为
Rt=ρv2SCt/2 (7)
式中:ρ为海水密度;S为湿面积。S由文献[9]提供的减量法计算:
S=LwlBT1T+2B+2Lwl-4.31Cb-12/3 (8)
式中:为排水体积,m3。
采用Fluent模拟船模在0.436,0.581,0.872,0.945,1.017,1.090,1.163 m/s這7个航速下的运动状态。船模与实船的缩尺比为1∶50,故对应的实船航速为6 kn, 8 kn, 12 kn, 13 kn, 14 kn, 15 kn, 16 kn,其中12 kn为设计航速。在流体流过整个流域的过程中,阻力监视器监测的阻力值变化不大;基本稳定后,取相邻总阻力的平均值,所得船模数值见表1。
表1 船模数值
根据普鲁哈斯卡假设,取Fr在0.1与0.2之间
图1 拟合曲线
的摩擦阻力因数和总阻力因数,将Ctm/Cfm作为y轴坐标,
Fr4/Cfm作为x轴坐标作图,拟合出的曲线见图1。根
据式(2),可得k=0.211,b=
0.750 5。采用式(3)得到k=0.212,模拟误差仅为0.47%,说明本文模拟出的数值正确。
这样便把总阻力值与船型要素联系起来,总阻力值可用垂线间长Lpp,水线间长Lwl,型宽B,吃水T,方形系数Cb等要素表示出来,实现了参数化[10]。
2 EEDI参数化
EEDI的概念[11-12]如式(9)所示:
IEEDI=cFcSFCPmDHv (9)
式中:cF为碳转换因子;cSFC为燃油消耗率;mDH为载质量;P为总功率。
EEDI与船舶主机功率和副机功率有关,主机功率为在无风无浪条件下75%的额定功率,副机功率是个大约值。若式(9)中的P约等于航行状态下的有效功率Pe,则等效能效指数[8-9]为
I′EEDI=cFcSFCPemDHvref (10)
式中:Pe=Rtv;vref为船舶航行状态下的航速。
mDH=Δ-m0
m0=(mh+mf+mm)(1+k′)
mh=chL1.657B0.777D0.282 5T0.045 7Cb0.014 56
mf=cfΔ
mm=cmPB(11)
式中:Δ为排水量;m0为空船质量;mh为钢料质量;mf为舾装质量;mm为机电设备质量;ch为钢料因数,取值为0.038 9;cf为木作舾装因数,取值为0.023 1;cm为机电质量因数,取值为0.112;k′为储备浮力因数,取值为0.045;L为船长;D为型深;PB为主机额定功率。
该船的主机使用的是MAN B&W 8L27/38,额定功率为2 640 kW,台数为3,使用重油航行,cF=3.114 4,cSFC=185 g/(kW·h);副机的cSFC=205 g/(kW·h);未使用轴带发电机与创新节能技术。
综上,该船的等效能效指数也可以用船型要素表示,同样实现了参数化。
3 多学科设计优化
3.1 多学科设计优化理论
多学科设计优化是一种设计优化的方法论,它最早是由美籍波兰人J Sobieszczanski-Sobieski提出的,随后NASA的Langley研究中心对多学科设计优化给出了定义:多学科设计优化是一种利用系统中相互作用的协同机制来设计复杂工程系统和子系统的方法论。它的主要思想就是通过分解、协调等手段将复杂工程系统分解为与现有工程设计组织形式相一致的若干子系统,从而利用现有的各学科分析设计工具及合适的优化策略,对复杂工程系统进行综合设计,实现复杂产品的功能需求,以达到缩短设计周期、降低开发成本、提高产品竞争力的目的。[13]
3.2 多学科设计优化方法
多学科设计优化模型设置见图2和3。
遗传算法是一种全局优化算法。得到初始种群后,给每个个体赋予一个适应度值,然后根据个体的适应度值来选择
优良的个体,并借助于遗传学中的遗传算子进行交叉和变异操作,得到代表新解集的种群。对新的种群再进行循环操作,经过若干代进化就可使种群趋于最佳,收敛于一个最适应环境的种群。该种群的个体经过解码后,就是该优化问题的最优解或者最优近似解。
由于传统的遗传算法在多目标处理上的不足,后来针对多目标问题衍生出NSGA。NSGA对传统的遗传算法进行了改进:在选择算子执行前,先根据
图4 NSGA-II流程
个体支配关系进行分层,为使适应度值规范化并维持种群的多样性,采用适应度共享和小生境技术。NSGA-Ⅱ在NSGA的基础上引入了精英策略,提出快速非支配排序方法,采取拥挤度和拥挤度比较算子,使算法的复杂度减小,同时加快了算法的执行速度,提高了优化结果的精度。NSGA-Ⅱ流程[14]如图4所示,其中:Gen为迭代次数,MaxGen为最大迭代次数。
3.3 优化过程和优化结果
优化目标:在设计航速下,Rt最小和I′EEDI最小。
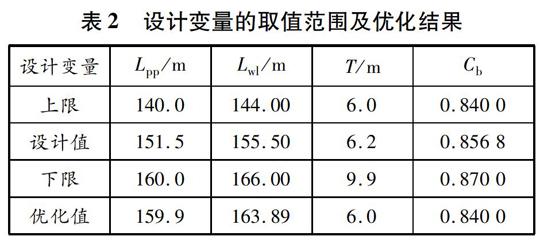
設计变量:主要是主尺度要素变量Lpp,Lwl,B,T和Cb。该船属于多用途船,对甲板上的布置有一定的要求,故要保证其型宽B(37.2 m)不变,而其他要素在设计值左右变化,具体取值范围见表2。
表2 设计变量的取值范围及优化结果
约束条件:除了设计变量的约束外,排水量
(31 496.9 t)、设计航速(12 kn)、海水密度、水的运动黏度系数、重力加速度、碳转换因子和燃油消耗率是不变的。
采用NSGA-II,种群规模为20,进化代数为30,交叉概率为0.9,交叉分布指数为10,变异分布指数为20。经过600次的迭代优化计算,整个优化过程如图5所示,圈起来的点即为最优解。选取这个最优解方案,优化结果见表2。原船与优化船的其他主尺度要素对比见表3。
图5 优化过程
表3 原船与优化船的其他主尺度要素对比
3.4 优化后的船型阻力及EEDI结果分析
根据式(1)~(8)可得到原船和优化船在相应航速下的总阻力因数和总阻力值,根据式(10)和(11)可得到各航速下优化船的EEDI,见表4。
从表4可以看出,优化船的阻力性能和EEDI
表4 原船与优化船的总阻力和EEDI比较
优于原船的阻力性能和EEDI,优化的目的已经达到。在航速偏低的情况下,原船与优化船的总阻力和EEDI几乎一致;在设计航速为12 kn时,船舶减阻9.29%,节能6.66%;随着航速的增加,减阻效果越发明显,节能效果无明显变化规律,这主要是由于影响EEDI的因素很多。
4 CFD数值模拟验证
采用Fluent对船型进行数值模拟。
图6~9为原船与优化船在航速为12 kn时的速度和动压力云图以及流线图对比。图6中,两船首部自由液面的速度云图虽然差别不很明显,但仍能看出原船首肩处的速度大于优化船的,这可能是因为进流段曲率过大而使肩波处受到不利干扰,兴波阻力增大,而优化船有效缓解了这一点。从图7可以明显看出,原船自由液面的速度波动更剧烈,这从侧面说明优化船的兴波阻力性能优于原船的。从图8可以看出,原船首尾的压差明显大于优化船的,这也说明原船的黏压阻力大于优化船的。从图9可以看出,优化船的船尾流线比原船的更加光滑、流畅,并且流线更向中部集中,适当缓解了艉部流线的分离现象[15]。这些云图、流线图均能在一定程度上反映优化船的阻力性能优于原船的。
图6 航速为12 kn时原船(左)和优化船(右)首部自由
液面速度云图
图7 航速为12 kn时原船(左)和优化船(右)自由液面
速度云图
图8 航速为12 kn时原船(左)和优化船(右)动压力云图
图9 航速为12 kn时原船(左)和优化船(右)船尾流线图
表5为原船与优化船的摩擦阻力、黏压阻力和兴波阻力的对比。从表5看出:主要是黏压阻力和兴波阻力的减小致使优化船总阻力小于原船总阻力;优化船的摩擦阻力大于原船的,这主要是因为优化船的长度增加且湿面积较大,但摩擦阻力增量较小。虽然优化船船长增加导致摩擦阻力增加,但相应的进流段和去流段的加长使艏艉曲率变小,缓解了艏艉可能出现的舭涡,进而使黏压阻力减少;船长的增加使得整艘船更加“瘦削”,这也有利于兴波阻力的减少。
表5 原船与优化船阻力比较
参数化的优化过程虽然只提供了一个寻优的依据,但也间接反映了各船型要素与阻力间的关系。结合图10,在本文设置的垂线间长、水线间长、吃水和方形系数的范围内,在排水量和型宽不变的情况下,总体分析船型要素对总阻力的影响。
c)方形系数
图10 船型要素与总阻力的关系
垂线间长的增加会导致总阻力的减小。垂线间长的增加必然会导致船长增加,雷诺数增加,摩擦阻力因数减小,湿面积增大,但总体摩擦阻力的增加是相对微小的,而且船长的增加相当于长宽比增加了,“瘦削”的船型会使黏压阻力和兴波阻力下降,且其下降值大于摩擦阻力的上升值,故总阻力下降。然而,在航速很低时,兴波阻力过小,甚至模拟结果为负值,船长的增加可能会导致总阻力增加。
吃水减小会导致总阻力减小。原船的吃水已经为6.2 m,为保证排水量不变,缩小的空间并不大,而且吃水的减小会在一定程度上减少湿面积,减小摩擦阻力。然而,吃水的选择通常不依据阻力性能,而从布置、稳性、航道和港口水深限制等方面考虑(若船舶吃水减小则航道和港口对其的限制就会减弱)。该船是肥大船且兼有打捞运输的功能,稍微减小其吃水就能对阻力有一定的改善且又满足了各航道的要求。
方形系数减小会导致总阻力减小。方形系数是表示船体水下部分肥瘦的一个重要标准。在排水量不变的情况下,减小方形系数,相当于让船变“瘦”,黏压阻力和兴波阻力会明显减小,但鉴于排水量、舱容、布置等的要求,方形系数不能过小。
5 结 论
本文阐述了多学科设计优化的技术理论,并且介绍了多学科设计优化的流程,对阻力和EEDI进行参数化分析后使用多学科设计优化算法对船型要素进行寻优,得到了优化的船型要素值。最后通过对原船进行船型变换,得到优化船。通过数值模拟,验证了优化船的阻力性能和EEDI确实优于原船的,达到了优化的目的。
由于软、硬件条件限制影响了CFD的计算精度,下一步的工作应进一步加强网格的划分,合理划分疏密有致的结构网格和非结构网格,流域的划分应再精简、分块,这样既能减少网格又能提高网格质量,有效提高模拟计算的精度。
在对EEDI的分析中,取主副机功率近似等于有效功率,因为减小阻力和降低能效指数的本质是相同的,所以结果分析着重于阻力性能分析。阻力性能的提高和推进效率的提高势必会带来主机功率的下降和EEDI的下降。
本文中原船的载质量为20 500 t,优化后载质量为20 190 t,载质量变小对船舶的经济性能有一定的不良影响。在接下来的工作中要考虑更多的指标,从技术、经济、环境等多方面对船型进行优化论证。
参考文献:
[1]金雁, 王丽铮, 陈顺怀. 川江及三峡库区变吃水干散货船的优化论证[J]. 船海工程, 2006(6): 44-47.
[2]张宝吉, 马坤, 纪卓尚. 基于遗传算法的最小阻力船型优化设计[J]. 船舶力学, 2011, 15(4): 325-331.
[3]刘寅东, 唐焕文, 李纪选. 船型多方案选优决策的层次分析方法[J]. 船舶工程, 1996(1): 22-25.
[4]金雁, 赵耀. 基于改进蚁群算法的船舶主尺度优化[J]. 华中科技大学学报(自然科学版), 2008, 36(11): 99-102.
[5]刘蔚. 多学科设计优化方法在7 000米载人潜水器总体设计中的应用[D]. 上海: 上海交通大学, 2007.
[6]张恒, 詹成胜, 刘祖源, 等. 基于船舶阻力性能的船型主尺度参数敏感度分析[J]. 船舶工程, 2015, 37(6): 11-14.
[7]姜次平. 船舶阻力的三因次换算方法[J]. 船舶工程, 1981(1): 7-11.
[8]宋家瑾, 周占群, 谢克振. 对肥大船估算形状因子实用方法的探讨[J]. 交通部上海船舶运输科学研究所学报, 1981, 1(1): 81-91.
[9]曾祥华, 王介文. 减量法求船舶湿面积[J]. 武汉造船, 1997, 3(1): 19-23.
[10]LI Dongqin, WILSONP A, ZHAO Xin. Establishment of effective metamodels for seakeeping performance in multidisciplinary ship design optimization[J]. Journal of Marine Science and Technology, 2016, 24(2): 233-243.
[11]刘继龙. 船舶能效设计指数分析[D]. 大连: 大连海事大学, 2013.
[12]LIU Shukui, SHANG Baoguo, PAPANIKOLAOU A, et al. Improved formula for estimating added resistance of ships in engineering application[J]. Journal of Marine Science and Application, 2016(4): 442-451
[13]張利. NSGA2算法及其在电力系统稳定器参数优化中的应用[D]. 成都: 西南交通大学, 2013.
[14]倪崇本. 基于CFD的船舶阻力性能综合研究[D]. 上海: 上海交通大学, 2012.
[15]刘英良. 基于CFD的超大型集装箱船线型优化研究[D]. 北京: 中国舰船研究院, 2014.
