无限滞后测度泛函微分方程解的有界性

李宝麟, 王云凤

(西北师范大学 数学与统计学院, 甘肃 兰州 730070)

1 预备知识

文献[1]介绍了一类新的方程,无限滞后测度泛函微分方程,并且证明了在一定条件下无限滞后测度泛函微分方程与广义常微分方程的等价关系.文献[2]研究了无限滞后测度泛函微分方程解对参数的连续依赖性;文献[3]建立了广义常微分方程新的有界性定理,并且获得了测度微分方程和时间尺度上的动力方程的解的有界性定理.

本文考虑无限滞后测度泛函微分方程解的有界性

Dy=f(yt,t)Dg,

(1)

其中Dy和Dg分别表示函数y和g的分布导数.在文献[4]中,方程(1)等价积分方程

(2)

其中,y是取值在Rn上的函数,ys:(-∞,0]→Rn,ys(τ)=y(s+τ)表示滞后的长度,方程(2)右端是关于不减函数g的Kurzweil-Henstock积分,g:[t0,+∞)→R为不减函数,

f:P×[t0,+∞)→Rn,

其中

P={yt:y∈O,t∈[t0,+∞)}⊂H0,
H0⊂G((-∞,0],Rn).

H0是Banach空间,G((-∞,0],Rn)是所有正则函数f的集合,f:(-∞,0]→Rn.无限滞后测度泛函微分方程满足的相空间H0⊂G((-∞,0],Rn)是线性空间,其中的范数为‖·‖,假设线性空间H0满足下列条件:

(H1)H0是完备的；

(H2) 如果y∈H0且t<0,则yt∈H0；

(H3) 存在有界函数k1:(-∞,0]→R+使得如果y∈H0且t≤0,则

‖y(t)‖≤k1(t)‖y‖；

(H4) 存在一个函数k2:(0,+∞)→[1,+∞)使得如果σ>0且y∈H0,t∈[-σ,0],则

‖y‖≤k2(σ)；

(H5) 存在有界函数k3:(-∞,0]→R+使得如果y∈H0且t≤0,则

‖yt‖≤k3(t)‖y‖；

(H6) 如果y∈H0,则函数t→‖yt‖在(-∞,0]上是正则的.

本文获得无限滞后测度泛函微分方程解的有界性结果是在广义常微分方程

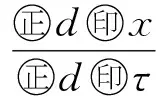
(3)

关于初值条件

x(s0)=x0

(4)

下新的有界性定理的基础上得到的.

2 广义常微分方程

τj∈[αi-1,αi]⊂(τj-δ(τj),τj+δ(τj)),

设X是Banach空间,O⊂X是开子集.

定义2.1[1]函数U:[a,b]×[a,b]→X称为在[a,b]上Henstock-Kurzweil可积的,如果存在I∈X,使得对任意的ε>0,存在正值函数

δ:[a,b]→(0,+∞),

使得对[a,b]上的任何的δ-精细分划

D={(τj,[αi-1,αi]),j=1,2,…,k},

其中

τj∈[αi-1,αi]⊂[τj-δ(τj),τj+δ(τj)],

有

(5)

则称I∈X为U在[a,b]上的Henstock-Kurzweil积分(也记为H-K积分),记作

特别地,当f:[a,b]→X,且

g:[a,b]→R,U(τ,t)=f(τ)g(t)

时,

设F:Ω→X,其中Ω=O×[t0,+∞).

定义2.2[1]设Ω⊂X×R是开集,(x,t)∈Ω,t∈R.称函数x:[a,b]→X为广义常微分方程

(6)

在区间[a,b]⊂R上的解,是指对所有的(x(t),t)∈Ω,且对每个s1,s2∈[a,b],有

成立.

定义2.3[3]函数x:[a,b]→X是广义常微分方程(6)关于初值条件x(s0)=z0的解,是指如果s0∈[a,b],(x(t),t)∈Ω对每个t,s∈[a,b],有

其中[a,b]⊂[t0,+∞).

引理2.4[3]如果

Ω=O×[t0,+∞),F∈F(Ω,h),

函数h是不减且左连续的,则对每个(z0,s0)∈Ω,广义常微分方程(6)在[s0,+∞)上存在唯一最大解并且x(s0)=z0.

注2.1对每个(z0,s0)∈Ω,把广义常微分方程的唯一最大解记为x(s,s0,z0)且x(s0)=z0.

定义2.5[3]广义常微分方程(6)是

1) 一致有界:如果对每个α>0,存在M=M(α)>0使得对每个s0∈[t0,+∞)及所有的

z0∈X, ‖z0‖<α,

有

‖x(s,s0,z0)‖

2) 拟一致最终有界:如果存在B>0,使得对每个α>0,存在T=T(α)>0,使得对所有的s0∈[t0,+∞)及

z0∈X, ‖z0‖<α,

有

‖x(s,s0,z0)‖

3) 一致最终有界:广义常微分方程是一致有界且拟一致最终有界.

定理2.6[3]设函数V:[t0,+∞)×X→R,使得对每个在(α,β]上左连续的函数z:[α,β]→X,函数t→V(t,z(t)),t∈[α,β]在区间(α,β]上是左连续的.而且,假设V满足下列条件:

(i) 有2个单调递增的函数p,b:R+→R+,使得p(0)=b(0)=0，

和对每一对(t,z)∈[t0,+∞)×X,有

b(‖z‖)≤V(t,z)≤p(‖z‖)

成立.

(ii) 对每个广义常微分方程(6)的解

z:[s0,+∞)→X,s0≥t0

及每个s0≤t

V(s,z(s))-V(t,z(t))≤0,

则广义常微分方程(6)是一致有界的.

定理2.7[3]设函数V:[t0,+∞)×X→R,使得对每个在(α,β]上左连续的函数z:[α,β]→X,函数t→V(t,z(t)),t∈[α,β]在区间(α,β]上是左连续的和满足定理2.6的条件(i).而且,假设V满足下列条件:

(V1) 对每个

x,y:[α,β]→X, [α,β]⊂[t0,+∞)

在区间[α,β]上有界变差,及每个α≤s

成立,其中h1:[t0,+∞)→R为不减和左连续的函数;

(V2) 存在连续函数φ:X→R,φ(0)=0且

φ(x)>0,x≠0,

使得对每个广义常微分方程(6)的解

z:[s0,+∞)→X,s0≥t0

及每个s0≤t

V(s,z(s))-V(t,z(t))≤(s-t)(-φ(z(t))),

则广义常微分方程(6)是一致最终有界的.

3 无限滞后测度泛函微分方程解的有界性

设H0⊂G((-∞,0],Rn)是Banach空间,其中的范数为‖·‖,考虑无限滞后测度泛函微分方程

(7)

其中，t0∈R,f:P×[t0,+∞)→Rn，g:[t0,+∞)→R,

P={yt:y∈O,t∈[t0,+∞)},φ∈P.

假设f:P×[t0,+∞)→Rn满足下列条件:

(A) 对于每一个y∈O,积分

存在;

(B) 存在一个关于g的Kurzweil-Stieltjies可积函数M:[t0,+∞)→R+,满足

ddg(t),

其中y∈O,[a,b]⊂[t0,+∞);

(C) 存在一个关于g的Kurzweil-Stieltjies可积函数L:[t0,+∞)→R+,满足

dg(t)‖≤
dg(t),

其中y,z∈O,[a,b]⊂[t0,+∞)(假设右边的积分存在).

引理3.1设f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),g:[t0,+∞)→R是不减函数,定义F:O×[t0,+∞)→G(R,Rn)如下

(8)

则F∈F(Ω,h,k),其中,Ω=O×[t0,+∞),

h,k:[t0,+∞)→R,

dg(s),t∈[t0,+∞),

k(t)=k2(σ)(dg(s),
t∈[t0,+∞).

定理3.2设O是H的子集,且t≥t0时,具有延拓性质,

P={yt:y∈O,t∈[t0,+∞)},
φ∈P,g:[t0,+∞)→R

是不减函数,f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),且F:O×[t0,+∞)→G(R,Rn)取值于H.如果y∈O是无限滞后测度泛函微分方程的解

则函数x:[t0,+∞)→O,

是广义常微分方程

的解.

证明定理的证明在文献[1]定理3.14可见.

定理3.3设O是H的子集,且t≥t0时,具有延拓性质,

P={yt∶y∈O,t∈[t0,+∞)},
φ∈P,g:[t0,+∞)→R

是不减函数,f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),且F:O×[t0,+∞)→G(R,Rn)取值于H.如果x:[t0,+∞)→O是广义常微分方程的解

在初值条件下

则函数y∈O且

是无限滞后测度泛函微分方程

的解.

证明定理的证明在文献[1]定理3.15可见.

定理3.4设f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),g:[t0,+∞)→R是不减和左连续函数,则对每个(z0,s0)∈P×[t0,+∞),无限滞后测度泛函微分方程(7)在[s0,+∞)上存在唯一最大解并且y(s0)=z0.

证明考虑无限滞后测度泛函微分方程(7)

t∈[t0,+∞).根据假设,函数f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),g:[t0,+∞)→R是不减和左连续函数,则无限滞后测度泛函微分方程(7)等价于广义常微分方程

(9)

其中F由(8)式给出.

根据引理2.4,因为对每个

(z0,s0)∈O×[t0,+∞),

广义常微分微分方程(9)在[s0,+∞)上存在唯一最大解并且x(s0)=z0,而且根据定理3.3有

是无限滞后测度泛函微分方程

的解.因此,对每个(z0,s0)∈P×[t0,+∞),无限滞后测度泛函微分方程(7)在[s0,+∞)上存在唯一最大解并且y(s0)=z0.

注3.1同样的,对每个

(z0,s0)∈P×[t0,+∞),

把无限滞后测度泛函微分方程(7)的唯一最大解记为y(s,s0,z0)且y(s0)=z0.

定义3.5无限滞后测度泛函微分方程(7)是:

1) 一致有界:如果对每个α>0,存在M=M(α)>0,使得对每个s0∈[t0,+∞)及所有的z0∈Rn,‖z0‖<α,有

‖y(s,s0,z0)‖

2) 拟一致最终有界:如果存在B>0,使得对每个α>0,存在T=T(α)>0,使得对所有的s0∈[t0,+∞)及z0∈Rn,‖z0‖<α,有

‖y(s,s0,z0)‖

3) 一致最终有界:无限滞后测度泛函微分方程是一致有界且拟一致最终有界.

定理3.6设f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),g:[t0,+∞)→R在[t0,+∞)上是不减和左连续的.设函数

U:[t0,+∞)×Rn→R,

使得对每个在(α,β]上左连续的函数z:[α,β]→X,函数

t→U(t,z(t)),

t∈[α,β]在区间(α,β]上是左连续的.而且,假设U满足下列条件:

(i)有2个单调递增的函数p,b:R+→R+,使得p(0)=b(0)=0，

和对每一对(t,z)∈[t0,+∞)×Rn,有

b(‖z‖)≤U(t,z)≤p(‖z‖)

成立；

z:[s0,+∞)→X,s0≥t0

及每个s0≤t

U(s,z(s))-U(t,z(t))≤0,

则无限滞后测度泛函微分方程(7)是一致有界的.

证明对每个x∈O及t∈[t0,+∞),定义函数F:O×[t0,+∞)→G(R,Rn)如下：

(10)

根据假设,函数f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),g:[t0,+∞)→R是不减和左连续函数,则根据引理3.1得

F∈F(O×[t0,+∞),h,k),

其中函数

dg(s),t∈[t0,+∞)

和

dg(s),
t∈[t0,+∞).

函数t→U(t,z(t)),t∈[α,β]满足定理3.6的条件(i),则函数t→U(t,z(t)),t∈[α,β]满足定理2.6的条件(i).

z:[s0,+∞)→Rn,s0≥t0

是无限滞后测度泛函微分方程

dg(s),t∈[t0,+∞)

的解，则通过定理3.2,有

x(t)(ϑ)

是广义常微分方程

的解,其中函数F由(10)式给出.因此,函数t→U(t,z(t)),t∈[α,β]满足定理2.6的条件(ii).所以,函数t→U(t,z(t)),t∈[α,β]满足定理2.6的所有条件,则广义常微分方程

是一致有界的,其中函数F由(10)式给出.

最后,根据定理3.3,证明了无限滞后测度泛函微分方程(7)也是一致有界的.

定理3.7设f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),g:[t0,+∞)→R在[t0,+∞)上是不减和左连续的.设函数

U:[t0,+∞)×Rn→R,

使得对每个在(α,β]上左连续的函数z:[α,β]→X,函数t→U(t,z(t)),t∈[α,β]在区间(α,β]上是左连续的和满足定理3.6的条件(i).而且,假设U满足下列条件:

(U1)对每个

x,y:[α,β]→X, [α,β]⊂[t0,+∞)

在区间[α,β]上有界变差及每个α≤s

成立,其中U:[t0,+∞)→R是关于u局部Kurzweil-Henstock-Stietijes可积的函数；

(U2)存在连续函数φ:X→R,φ(0)=0且φ(x)>0,x≠0,使得对每个无限滞后测度泛函微分方程(7)的解

z:[s0,+∞)→X,s0≥t0

及每个s0≤t

U(s,z(s))-U(t,z(t))≤(s-t)(-φ(z(t))),

则无限滞后测度泛函微分方程(7)是一致最终有界的.

证明对每个x∈O及t∈[t0,+∞),定义函数F:O×[t0,+∞)→G(R,Rn)如下

(11)

根据假设,函数f:P×[t0,+∞)→Rn满足条件(A)、(B)和(C),g:[t0,+∞)→R是不减和左连续函数,则根据引理3.1得

F∈F(O×[t0,+∞),h,k),

其中函数

dg(s),t∈[t0,+∞),

k(t)=k2(σ)(dg(s),
t∈[t0,+∞).

因为函数t→U(t,z(t)),t∈[α,β]在区间(α,β]上是左连续的和满足定理3.6的条件(i),有2个单调递增的函数p,b:R+→R+,使得

p(0)=b(0)=0，

和对每一对(t,z)∈[t0,+∞)×Rn有

b(‖z‖)≤U(t,z)≤p(‖z‖)

成立.则函数U:t→U(t,z(t)),t∈[α,β]满足定理2.6的假设(i).

对每个t∈[t0,+∞),定义函数

h1(t):[t0,+∞)→R

如下

du(t),t∈[t0,+∞),

则函数h1是不减且左连续的.

而且由条件(U1)有,函数

U:t→U(t,z(t)),t∈[α,β]

满足下列条件

对每个α≤s

其次,由条件(U2)有

z:[s0,+∞]→Rn,s0≥t0

是无限滞后测度泛函微分方程

dg(s),
t∈[t0,+∞)

的解.

则通过定理3.2有

是广义常微分方程

的解,其中函数F由(11)式给出.

因此,函数t→U(t,z(t)),t∈[α,β]满足定理2.7的条件(V2).

所以,函数t→U(t,z(t)),t∈[α,β]满足定理2.7的所有条件,则广义常微分方程

是一致最终有界的,其中函数F由(11)式给出.

最后,根据定理3.3,证明了无限滞后测度泛函微分方程(7)也是一致最终有界的.

[3] FEDERSON M, GRAU R, MESQUITA J G, et al. Boundedeness of solutions of measure differential equations and dynamic equations on time scales[J]. J Diff Eqns,2017,263(1):26-56.

[4] FEDERSON M, MESQUITA J G, SLAVK A. Measure functional differential equations and functional dynamic equations on time scales[J]. J Diff Eqns,2012,252(6):3816-3847.

[6] PURNA C D, RISHI R S. Existence and stability of measure differential equations[J]. Czechoslovak Math J,1972,22(97):145-158.

[7] HINO Y, MURAKAMI S, NAITO T. Functional Differential Equations with Infinite Delay[M]. New York:Springer-Verlag,1991.

[8] KURZWEIL J. Genenralized ordinary differential equations and continuous dependence on a parameter[J]. Czechoslovak Math J,1957,82(7):418-448.

[9] KURZWEIL J. Generalized ordinary differential equations[J]. Czechoslovak Math J,1958,83(8):360-389.

[10] FEDERSON M, SCHWABIK. Generalized ODE approach to impulsive retarded functional differential equations[J]. Diff Integ Eqns,2006,19(11):1201-1234.