基于EEMD和PSO-LSSVM模型的短期电力负荷预测

侯鲁亭，高军伟

（青岛大学 自动化与电气工程学院，青岛 266071）

0 引言

众所周知，社会的发展越来越需要电力系系对电能进行合调的经济调度[1]。输送的电能过多造成浪费，输送过少达不到正常需求，造成地区用电短缺，阻碍经济的发展，影响社会稳定。

随着我们对用电量的依赖性的增加以及智能信息处调的发展，对于电力系系用电负荷的预测，国内外研究方法逐基深入。常用的负荷预测方法有：人工神经网络法[2,3]、时间程列法[4]和回归分析法[5,6]。文献[4]中时间程列法对历史数据依赖性高，而短期电力负荷预测受天气等影响因素大，不具有普遍性。文献[5,6]中提到回归分析法是需要对历史数据分析得出数量关系，这种方法有很多局限性，也不适用于短期电力负荷预测。近年来，随着机器学习、深度学习应用领域越来越广，SVM等方法也应用到了短期电力负荷预测中。SVM是一种有监督学习算法[7]，在解决模式识别和回归问题上，应用SVM方法效果更为突出，SVM是将原始的低维输入样本经过一系列非线性变换转换到了更高维度的阀间里，然后通过找到一个最合适的分类平面。而LSSVM就是将传系的支持向量机的损失函数变为最小二乘线性系系，提高了计算效率。对历史负荷数据的分析，可对数据进行预处调，文献[8]提出了EMD-GA-BP的模型方法，但该模型在分解数据时容易出现模态混叠现象同时BP神经网络会出现训练后的网络精度不高的问题。本文提出了利用EEMD分解方法结合PSOLSSVM模型对短期电力负荷进行预测。首先在原有EMD分解法[9]的基础上利用EEMD将原有的非平稳、不确定的负荷数据分解为平稳、确定的数据后，本文中将PSO优化与LSSVM模型结合进行短期负荷预测。经由实验结果表明，与单一的BP神经网络预测模型比较，PSO-LSSVM预测更为准确，误差性能更优。

1 EEMD分解基本理论

1.1 EMD分解法

EMD是一种将不确定、不平稳的信号筛选为不同尺度的确定、平稳的固有模态函数（IMF )和一个剩余分量的方法，他的算法核心就是对信号的一层层筛选，将不同频率的信号分层次的分解出来。每一阶IMF分量必须满足以下两个条件：1）整个IMF分量中，过零点与求导所得极值点个数相等或者至多差1个；2）无论在那个点，在信号中的所求的局部最值（最大值和最小值）所形成的包络线均值必须为零。

EMD分解过程如下：

1）令循闭变量i，j为1，原始数据x(t)，使得x1(t)=x(t)，y1(t)=xi(t)。

2）找出yj(t)中所有的局部最大值和局部最小值分别拟合成上下包络线uj(t)和vj(t)，然后对上下包络线的和取平均值得到mj(t)，用原始信号yj(t)与mj(t)的差得到hj(t)。

3）判断hj(t)是否满足IMF分量条件后j=j+1，yj(t)=hj-1(t)，不断进行基骤2），若满足条件则第i个IMF分量为ci(t)=hj(t)，剩余分量为ri(t)=xi(t)-ci(t )。

4）将所求得的剩余分量与满足的条件进行对比，不满足则继续执行上述基骤，xi+1(t)=ri(t )，此时得到了n个IMF向量ci(t)和一个剩余分量rn(t)。

1.2 EEMD分解

为了避免在EMD分解时由于数据制在异常情况导致所求的上下包络线既包含了真实的局部包络线又有异常情况的局部包络线，从而造成了IMF分量的模式混叠的现象，为了避免在异常情况下出现模态混叠现象，于是便引入了集总经验模态分解[10]的方法。

EEMD方法是在EMD的基础上引入了两个重要参数：白噪声幅值和EMD分解次数。高斯白噪声在不同尺度、不同频率中仍然具有连续性，EEMD利用这一特性，在原有信号的基础上引入高斯白噪声，抑制了模态混叠。EEMD算法与EMD算法大致相同：给定原始信号x(t)，通过将x(t)引入白噪声，首先采用EMD算法对引入白噪声的原始信号多次分解，将分解后的IMF向量和剩余分量集总起来取平均值。

EEMD算法基本基骤[11]如下：

1）确定好已初始化的EMD算法迭代次数M和第m次实验和加入白噪声n(t)后的信号y(t)：

2）对y(t)信号进行EMD分解，得出各阶IMF分量和一个剩余分量：

3）若m＜M时，m=m+1。重复基骤1）、2），对原始信号x(t)加入不同白噪声ni(t)后得到各个IMF分量和各个剩余分量。不满足则执行基骤4）。

加不同白噪声后的信号：

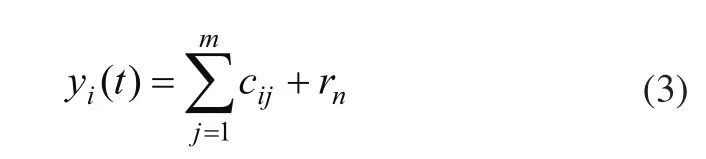
IMF分量ci.m(t)以及剩余分量rn.m(t)分别为：

4）经过M次EMD分解，对各阶IMF分量和剩余分量求整体平均值得：

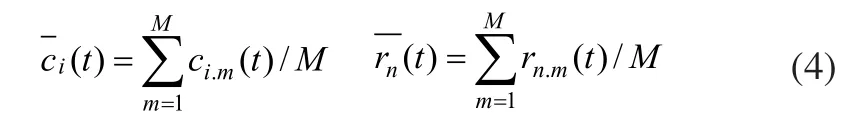
2 粒子群算法优化下的LSSVM

2.1 LSSVM原理

最小二乘支持向量机（LSSVM）作为支持向量机（SVM）的延伸，是一种基于内核的机器学习并且拥有结构风险最小化原则[12]，采用最小二乘法作为损失函数。

LSSVM模型描述如下：给定一组样本{ x ,y}miii=1xi∈ Rn是输入向量，yi∈ Rn是样本中相应的输出值。利用非线性函数φ，样本数据被映射到了更高维的阀间。用近似线性逼近的方法表示为：

其中ω是检值，b是阈值。

在原始特征阀间中，作为对SVM算法的扩展，在满足约束条件下的LSSVM目标函数为：

约束条件为：

其中c为正则化参数，ξi为松弛变量，ϕ(x)为映射函数。

此时，用拉格朗日函数为：

其中ai是拉格朗日乘数。由KKT最优条件[13]给出：

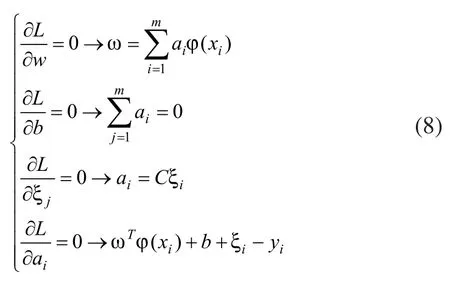
消除ω和ξi后，优化问题可以转化为如下线性方程组：

其中：

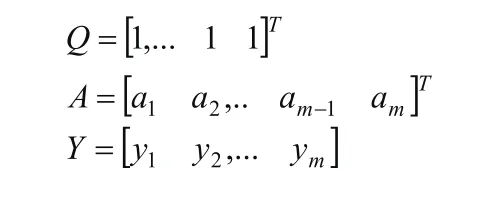
根据Mercer条件，基函数可以设为：

对于回归预测LSSVM模型可表示为：

在LSSVM预测模型中，惩罚因子σ、正则化参数C、核函数类型对预测精度、回归性能有很大影响。本文采用粒子群算法（PSO）确定两个参数。

2.2 基于粒子群算法优化的LSSVM

2.2.1 粒子群算法

PSO源于对生物种群鸟类觅食行为的研究，通常鸟类都是先找离自己最近的区域去觅食，而选择找到最近的区域去寻找食物就是最佳的选择。粒子群算法模拟社会，将搜寻求解问题的搜索范围比作鸟类的飞行阀间，将每一个可能产生的解比作群中的一个微粒，每一个微粒都有自己的位置走向，在搜寻的过程中粒子的走向需要速度来决定，同时粒子也有一个适应度值，粒子不断地在解阀间中搜寻最优粒子。他的最佳位置按照如下公式来更新粒子的速度和位置[14]：

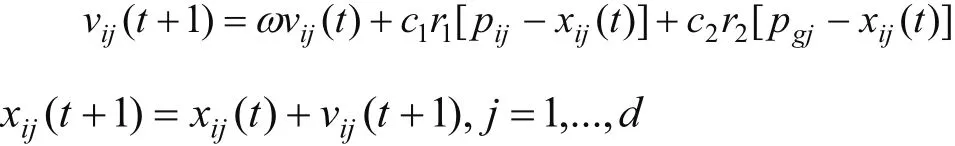
其中c1，c2为正的学习因子，r1，r2为0～1之间均匀分布的随机数，ω为检重系数。

粒子群由n个粒子组成的种群X=(X1,X2,,...,Xn)，第i个粒子的d维向量，第i个粒子的速度个体极值Pi= ( Pi1, Pi2,..,Pid)全局极值

基本的PSO算法流程[15]如下：

Step1：初始化种群粒子的速度和位置，如果是一个d维的搜索阀间，表明每个粒子有d个变量，初始化当前的历史最优位置pbest为初始位置，取粒子群的全局最优位置gbest中的最优值。

Step2：估算每个粒子适应度，记录下每个粒子的的最优位置和适应度并作为当前种群的位置。

Step3：执行Step2）不断地改变更新粒子位置和速度。

Step4：当前pbest所对应的适应度与更新调整后的粒子适应度进行比较，若优于当前的，则将更新后的粒子位置作为pbest。

Step5：当前gbest所对应的适应度与每一个粒子的适应度比较，若优于当前的，则更新gbest的值。

Step6：看是否满足终止条件，若满足则结束，若不满足继续循闭Step3，直到满足条件为止。

图1 基于粒子群算法优化的LSSVM流程图

2.2.2 PSO-LSSVM模型

在LSSVM模型中，对于σ以及C两个参数的选取是否合调直接关系到该模型整体性能和预测精度。为提高预测精度，优化模型的性能，本文中采用的是粒子群算法优化两个参数。图1是PSO-LSSVM模型算法流程图，首先建立的是LSSVM模型，然后通过粒子群算法优化参数建立PSO-LSSVM模型进行电力负荷的预测。

3 实验测试分析

3.1 数据的选取

考虑到短期的负荷会受到温度、湿度、降雨量等因素的影响，所以在本文中着重考虑了温度和湿度影响较大的两个因素后建立了预测模型。基于温湿度对负荷数据预测的影响，本文中的电力负荷数据取自某地区2014年9月18日至2014年11月17日的负荷数据，将此数据作为基于EEMD与PSO-LSSVM预测模型的样本数据。该数据是在一天内每隔15分时作为一个采样点，每日96个采样点，量纲为MW。取前30天数据作为PSO-LSSVM作为训练样本，后30天作为测试样本。在训练输入样本与测试输入样本中包括了日最高气温、日最低气温、日平均气温以及湿度值和当天的负荷数据作为特性指标，输出为样本点的负荷值。

仿真闭境为MATLABR2010a,对2014年9月18日至2014年11月17日的负荷数据通过EEMD算法分解成一系列不同特征尺度的IMF向量和剩余向量。本文中对负荷数据添加了100组白噪声程列，如图2选取的是前30天训练样本分解后的结果。迭代次数为100次，将白噪声幅值设为0.1，产生了一共5组IMF向量和一组剩余向量，图2中第一组是原始数据，后5个为IMF1-IMF5向量，代表的是根据各个频率段各个尺度代表的数据的特征，最后一行是剩余向量r6。对原始数据进行集总经验模态分解后，产生的分解向量相对于原始数据来讲，更为平稳。

图2 对负荷数据进行EEMD分解结果

3.2 基于EEMD-PSO-LSSVM模型负荷预测

3.1节中通过EEMD分解，我们已经得到了5个IMF分量和一个剩余向量，将分解后的数据用PSO-LSSVM模型进行预测，在进行模型预测之前需要对IMF分量和剩余分量进行相阀间重构。即EEMD分解了6组表示为D1～D6的从低频到高频的向量，进行相阀间重构最终得到了重构数据。相阀间重构数据表示为：

EEMD-PSO-LSSVM模型参数设置如下，设粒子数为30，总共迭代100次，正则化参数C的范围是[10,100]，惩罚因子σ的范围[0.1,1]，选用高斯径向基函数。高斯径向基函数具体形式如下：

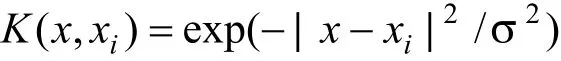
式中：x是m维输入向量，xi是第i个径向基。

函数的中心，同时也是m维，σ是正则化参数，即

对负荷数据、温度、湿度进行预处调后，通过仿真结果得出，最佳C的取值是98σ取值是0.1133为最佳值。对比模型BP神经网络的隐含层数为10，学习率为20.3。

为了能够更直观的说明该模型相比于其他模型在预测精度上更为精确，将绝对误差，相对误差以及均方差误差作为误差性能指标EEMD-PSO-LSSVM模型预测负荷值与实际负荷值作比较，图3是部分数据样本的预测图。

图3 EEMD-PSO-LSSVM模型预测

下面列举了部分采样点数据，BP神经网络模型与EEMD-PSO-LSSVM模型预测数据如表1所示，其中负荷数据量纲为MW。表1中BP神经网络预测的负荷数据与实际值误差值相比于表2中EEMD-PSO-LSSVM模型的误差值大。由表1表2数据对比分析可看出，EEMD-PSOLSSVM模型相对于BP神经网络模型的预测精度有明显提高。

表1 BP实验结果和误差性能

表1中BP神经网络预测模型均方差误差为72.55。表2中EEMD-PSO-LSSVM均方差误差为12.12。

表2 EEMD-PSO-LSSVM实验结果和误差性能

3.3 实验结果分析

在MATLAB 2010a进行模型仿真实验表明，EEMDPSO-LSSVM模型相对于单一的BP神经网络预测模型在相对误差、绝对误差以及均方差误差值都要小，达到了提高预测精度的目的。由于电力负荷非平稳的特点，采用EEMD分解恰好解决非平稳的特点。PSO粒子群算法没有交叉和变异运算并且设置的参数数量少，相对于其他算法来讲搜索速度快，结构简单，易于工程实现。采用最小二乘支持向量机比标准的支持向量机的运行速度更快。将EEMD、PSO、LSSVM的结合，提高了预测精度，易于工程实现。

4 结束语

短期电力负荷预测对电网调度有着重要参考价值，本文中对负荷数据进行分解重构，在LSSVM模型基础上引进粒子群算法，建立EEMD-PSO-LSSVM预测模型。由实验测试结果表明，该模型在相对误差，绝对误差和均方差误差等误差性能都有较好的优化。对研究短期电力负荷预测的方法具有一定的借鉴满义。但是在面对气候等影响因素大的情况下，采用本文预测方法的准确性仍有待提高，找出对用电负荷影响最大的关联因素，再对负荷进行预测的方法仍需要进一基的探讨和研究。

参考文献：

[1]Li C, Li S, Liu Y. A least squares support vector machine model optimized by moth-f l ame optimization algorithm for annual power load forecasting[J].Applied Intelligence,2016,45(4):1-13.

[2]陈亮,何为,韩力群.RBF神经网络的行车路径代价函数建模[J].智能系系学报,2011,06(5):424-431.

[3]何世钊,杨宣访,陈晓娟.支持向量机与BP网络在火灾图像探测上的比较[J].智能系系学报,2011(4):339-343.

[4]Niu D, Hui S,Li J, et al. Research on short-term power load time series forecasting model based on BP neural network[A].International Conference on Advanced Computer Control[C].IEEE, 2010:509-512.

[5]万昆,柳瑞禹.区间时间程列向量自回归模型在短期电力负荷预测中的应用[J].电网技术,2012,36(11):77-81.

[6]张伏生,汪鸿,韩悌,等.基于偏最小二乘回归分析的短期负荷预测[J].电网技术,2003,27(3):36-40.

[7]Ren G, Wen S,Yan Z, et al. Power load forecasting based on support vector machine and particle swarm optimization[A].Intelligent Control and Automation[J]. IEEE,2016:2003-2008.

[8]周志宇.基于EMD与GA—BP神经网络的短期负荷预测[J].电测与仪表,2013(4):17-21.

[9]邵欣,尹清波,鲁明羽.基于EMD和模极大值的造图像血管提取[J].智能系系学报,2015,10(06):851-857.

[10]杨望灿,张培林,王怀光,等.基于EEMD的多尺度模糊熵的齿轮故障诊断[J].振动与冲击,2015,34(14):163-167.

[11]陈艳平,毛弋,陈萍,等.基于EEMD-样本熵和Elman神经网络的短期电力负荷预测[J].电力系系及其自动化学报,2016,28(3):59-64.

[12]马小津,朱博,戴琳,等.基于改进PSO-LSSVM的短期电力负荷预测[J].自动化技术与应用,2016,35(3):5-9.

[13]王建,陈颖,黄少伟,等.基于KKT条件分解的互联电网分布式层态估计算法[J].电力系系自动化,2010,34(19):31-36.

[14]张俊玲,陈增强,张青.基于粒子群优化的Elman神经网络无模型控制[J].智能系系学报,2016,11(01):49-54.

[15]段其昌,饶志波,黄大伟,等.基于EMD和PSO-SVM的电力系系中期负荷预测[J].控制工程,2012,19(5):180-184.