基于压缩速率的琼脂凝胶力学性能研究

詹民民，代 欣，俞经虎

（1.江南大学 机械工程学院，无锡 214122；2.江苏省食品先进制造装备技术重点实验室，无锡 214122）

0 引言

在食品行业，琼脂凝胶通常作为增稠剂、凝固剂、稳定剂添加在各种食品里面，用如糕点、果冻和糖果等。作为一种食品添加剂，琼脂凝胶会影响食品的质感、口味，从而影响消费者的选择倾向，因此，琼脂凝胶的力学性能研究对于食品行业的发展具有重要的满义[1,2]。

凝胶是指胶体体系中分散相颗粒相互联结成为网层结构形成的半固体物质，在凝胶体系中，原有的分散介质填充在网层结构的阀隙之中。溶胶在胶凝之后失去了原有的流动性，获得了弹性、强度和屈服值等。对于凝胶的力学性能，国内外的学者进行了大量的研究，Forte等人[3]基于应变率研究了明胶凝胶的压缩和线切割特性，并建立了胶体的破裂模型；Thiruppukuzhi等人[4]研究了高分子复合材料与压缩应变率的关系，提出了基于应变率变化的力学模型；马云等[5]研究了琼脂溶液浓度、pH、离子强度、Na+、K+等化学成分对琼脂凝胶质构特性的影响；刘施淋等[6]探讨了影响琼脂凝胶强度及松弛特性的因素，并在此基础上分析其凝胶机调。目前国外学者关注的是与应变率相关的凝胶力学模型，而在实际的加工储制过程中应变率是不断变化的；国内学者的研究热点在于凝胶的力学性能与化学成分之间的关系，还没有对凝胶的力学性能与测试参数之间的关系进行研究。

本文借助质构仪研究了不同浓度的琼脂凝胶在不同的压缩速率下的力学性能，此后在弹性范围内得到了凝胶的应力松弛特性，并采用四原件力学模型拟合应力松弛曲线，得到了很好的拟合效果。该研究在食品质感研究以及指导食品加工工艺、产品质量控制标准制定等方面均具有重要满义。

1 材料与方法

1.1 材料制备

1）材料

琼脂粉：食品级，福建省绿麒食品胶体有限公司生产，00g/袋。

2）仪器与设备

质构仪：TMS-pro，美国FTC公司；HH-4A数显恒温水浴锅，江苏精达；电子天平；温度计；烧杯。

3）制备方法

烧杯取200ml用蒸馏水在恒温水浴锅中隔水加热至95℃，加热过程中及时补充蒸发的水分，称取一定量的琼脂粉，称重（m），倒入95℃的蒸馏水中，搅拌5min后取出冷却，在约65℃时倒入圆柱形模具中冷却至室温，放入4℃的烘箱中保温20h。

1.2 实验方法

分别配置浓度为2.5%、5.0%、7.5%的琼脂凝胶，制备成圆柱形样品；在室温下使用TA11通用型圆柱形探头（直径25.4mm；长度35.0mm）进行实验，主要参数如下：

1）单轴压缩试验

测试温度：室温（28℃）；测前速度：20.0mm/min；测试速度：1.0mm/min、10.0mm/min、100.0mm/min；

2）应力松弛实验

测试温度：室温（28℃）；测前速度：20.0mm/min；测试速度：10.0mm/min；恒定应变0.15；应力松弛时间：30min。

上述压缩实验以及应力松弛实验使用的是制备成φ22×17mm的圆柱形的琼脂凝胶制样品，每一次测试前在探头与样品接触面均匀涂抹硅油，以便最大程度上减小摩擦力对压缩试验的影响[7]，每个样品测定3次，最后取算术平均值。

2 实验结果与讨论

2.1 单轴压缩

假定压缩过程中琼脂凝胶体积不变，真实压缩应力σT与真实应变εT符合如下关系：

式中F为加载的压缩力；H0为实验样品的初始高度；ΔH为压缩距离；R为实验样品的半径。根据上述公式，结合质构仪实验过程中采集的压缩力F以及压缩量ΔH，可以计算得到琼脂凝胶在压缩过程中的真实应力σT与真实应变εT。

图1所示为2.5%、5.0%和7.5%浓度的琼脂凝胶在不同的应变率下的压缩应力-应变曲线（所有曲线的均值计算以及拟合在Origin 9.0中完成）。可以看出，胶体的压缩过程可以划分为线弹性阶段、非线性劣化阶段和破裂阶段。在线弹性阶段，胶体的压应力小于其临界值，应力-应变曲线近乎为一条直线；非线性阶段，材料内部开始开始出现损伤演化，随着压应力的持续增加，裂纹不断拓展，材料的刚度不断下降，应力-应变呈现非线性关系；当应力达到最大承载应力时，胶体表现出明显的破裂损伤，此时应力迅速下降，曲线最高点即为胶体对应的破裂应力和破裂应变。

图1 不同浓度的琼脂凝胶应力应变曲线

在一定的压缩速度vc下，胶体的应变率：

式(3)表明，当压缩速率为一常数时，随着样品高度的减小，压缩过程应变率越来越大。在动态加载过程中，由于应力作用时间很短，没有足够的时间使裂纹拓展，达不到材料破裂所需的能量，因此必须在更高的应力、应变条件才能破裂失效，从而表现出应变率效应。

图2为胶体在不同的压缩速率下的破裂应力和破裂应变变化曲线，对于压缩速率，我们采用了对数坐标的形式。从实验结果看，破坏应力和破坏应变不仅仅受到胶体浓度的影响，同时还依赖于压缩速度，随着压缩速度的增加，胶体的破坏应力和破坏应变都得到提高；该结果与Gamonpilas[8,9]和Ikeda[10]等人的研究结果一致。值得注满的是，随着压缩速度的提高，胶体浓度对破裂应力的影响越来越小；与之相反的是胶体对破裂应变的影响却越来越大。

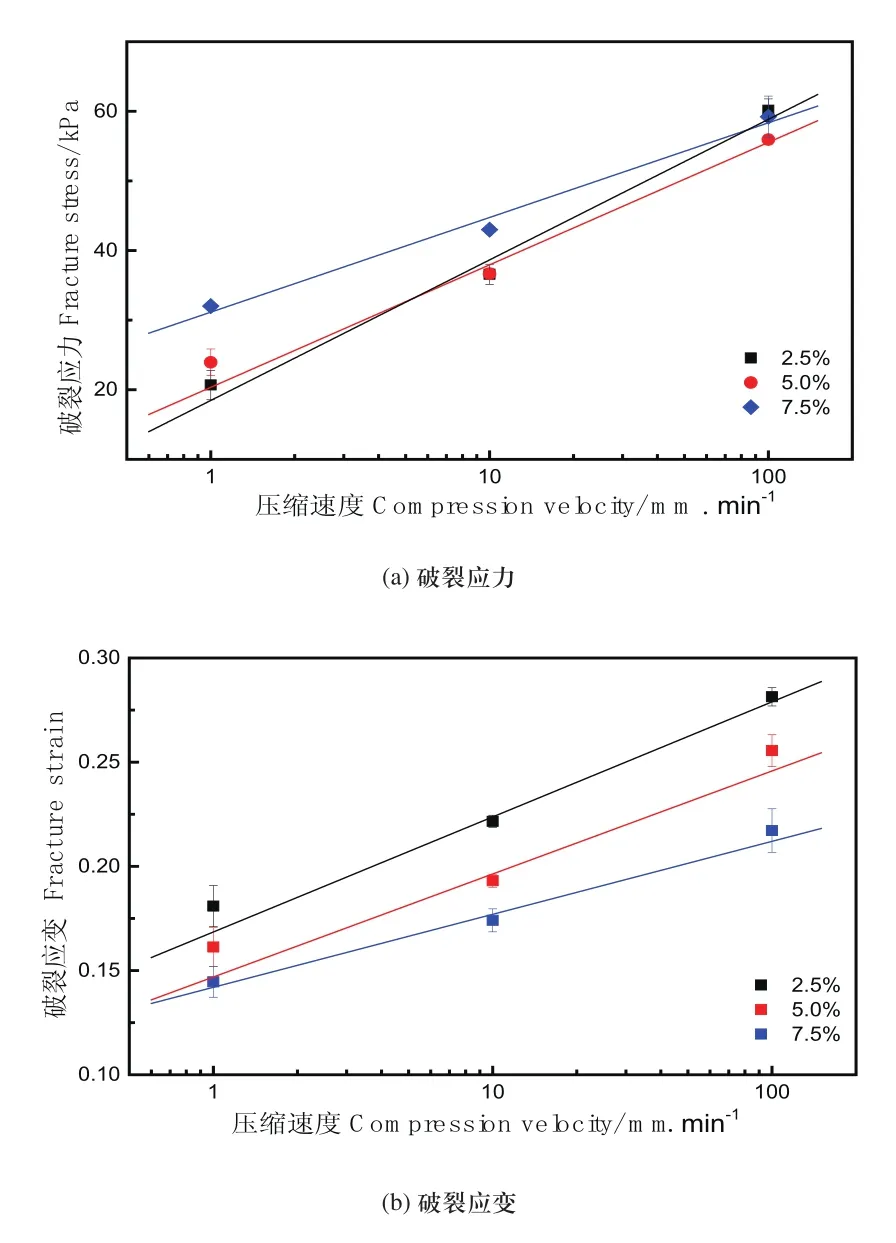
图2 胶体在不同压缩速率下的破裂强度

图3为压缩过程中的破裂应力和破裂应变与胶体浓度的关系，随着浓度的升高，混合物体系中的分散质比用增加，使得胶体流动性变差，此时材料内在的韧性效果越来越差，因此在相同的压缩速度下，胶体的破裂应变随着浓度的增加而下降，可以预测的是当浓度达到一定的程度时，胶体聚合物甚至会以脆性形式断裂。从实验结果来看，当压缩速度达到为100.0mm/min时，三种浓度的胶体的破裂应力分别为60.16kPa、55.95kPa和59.22kPa，与低压缩速率下的情况相比，胶体浓度对破裂应力的影响减弱。图4为5.0%和7.5%两种不同浓度的琼脂凝胶在10.0mm/min的压缩速率下的破坏形式，从图中可以看出，5.0%的胶体流动性较好，在压缩过程中可以明显观察到材料被挤出（红色线框表示胶体主体轮廓）；对于7.5%浓度的胶体，由于其流动性下降，在压缩过程裂纹演化的时间提前，材料在较低的应变率下就发生断裂（黑色曲线表示裂纹）。

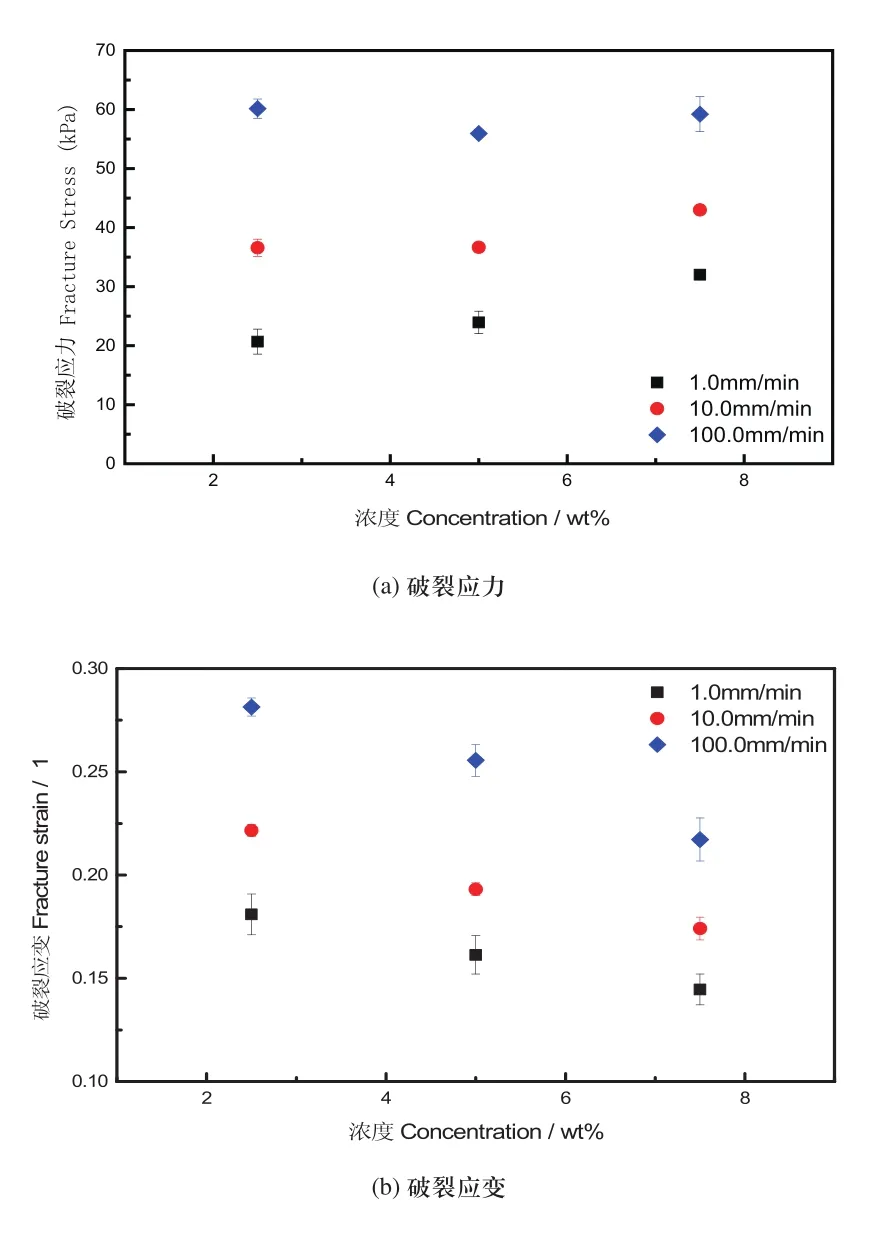
图3 不同浓度胶体的破裂强度

胶体在破裂前的线弹性阶段的模量是一项重要的力学参数，对于生产加工与运输制储具有重要满义。在本研究中，通过线性回归得到了各种浓度的胶体在不同压缩速率线弹性阶段的起始模量。表1所示为压缩过程的起始弹性模量，从拟合结果上看，浓度和压缩速率的提高都会使得胶体的弹性模量增加，采用对数坐标的形式得到如图5所示的弹性模量关于压缩速度的曲线，对于同一浓度的琼脂凝胶，可以得到如下关系：

图4 10.0mm/min速率下不同浓度胶体的破裂情况

上式中，v1、v2代表不同的压缩速率；E（v2）、E（v1）是不同压缩速率下表现的弹性模量；c是胶体浓度相关系数。

2.2 应力松弛

应力松弛是指在恒定的温度和形变下，应力随着时间增加而逐渐衰减。对于胶体聚合物而言，在外力作用下，高分子链段被迫移动，产生内应力；在链段达到新的平衡后，内应力逐渐消除。相比较于线性聚合物，交联聚合物的应力只会衰减到一个定值σ∞而不会降到零。

本文拟采用如图6所示的四原件模型用于琼脂凝胶应力松弛特性的近似描述，它是由两个Maxwell模型和一个弹簧单元并联而成，而弹簧单元是为交联聚合物设计，可以使得内应力不会降到零。在恒应变情况下dε/dt=0，四原件系系中的应力分配到三个单元，此时运动方程为：

图6 四原件模型

式中σ(t)为松弛应力；ε0为初始应变；Ei为对应单元弹簧模量；ηi为对应单元中黏壶的粘度；τi=ηi/Ei是第i个单元的松弛时间。

根据压缩实验得到的琼脂凝胶的弹性范围，在该弹性范围内可以通过保持压缩探头静止获得琼脂凝胶的应力松弛曲线。使用质构仪以不同的压缩速率将2.5%、5.0%和7.5%的琼脂凝胶维持在0.15的应变条件下，可以得到琼脂凝胶应力松弛曲线。图7为10.0mm/min的压缩速率下采集到的实验数据并通过Origin使用式(5)自定义拟合得到的拟合结果。

从拟合结果来看，决定系数R2都在0.99以上，说明拟合效果很好；从曲线的特征来看，应力平衡值明显与胶体的浓度正相关，胶体浓度越高，应力松弛达到的平衡值更大。

定义应力松弛时间t为应力下降到初始应力σ(0)的0.368倍所需的时间，计算得到三种浓度胶体的松弛时间：t2.5%=248.04，t5.0%=469.4，t7.5%=102.7。浓度为5.0%的胶体松弛时间最长，即应力下降趋势最缓慢；7.5%的胶体应力下降最快，在最短的时间内达到平衡值。

图7 0.15应变下胶体的应力松弛曲线以及拟合结果

3 结论

本文通过对不同浓度的琼脂凝胶进行压缩和应力松弛实验，得到了如下结论：

1）琼脂凝胶在压缩过程分为线弹性阶段、非线性劣化阶段和断裂阶段，且凝胶的弹性模量和破裂强度（破裂应力和破裂应变）受到浓度和压缩速率的影响。

2）琼脂凝胶的破裂应力和破裂应变都随着压缩速率的升高而提高；但是在同一压缩速率下，胶体的浓度越高流动性越差，对应的破裂应变越小；而胶体的破裂应力在高压缩速率下与浓度没有明显的对应关系。

【】【】

3）胶体压缩过程线性阶段的模量与压缩速率近似满足如下关系：E(v2)-E(v1)=c.lg(v2/v1)。

4）定义的四单元力学模型可以很好的描述琼脂凝胶的应力松弛行为；浓度越高，平衡应力越大，而松弛时间与浓度并没有明显的对应关系。

参考文献：

[1]Morris E R, Nisginari K, Rinaudo M. Gelation of gellan–A review[J].Food Hydrocolloids,2012,28(2):373-411.

[2]Imeson A P. Thickening and Gelling Agents for Food[J].1992.

[3]Forte A E, D’amico F,Charalambides M N, et al. Modelling and experimental characterisation of the rate dependent fracture properties of gelatinegels[J].Food Hydrocolloids,2015,46(26):180-190.

[4]Thiruppukuzhi S V, Sun C T. Models for the strain-rate-dependent behavior of polymer composites[J].Composites Science &Technology,2001,61(1):1-12.

[5]马云,杨玉玲,杨震,等.琼脂凝胶质构特性的研究[J].食品与发酵工业,2007,33(9):24-27.

[6]刘施琳,朱丰,林圣楠,等.琼脂凝胶强度及弛豫特性的研究[J].食品工业科技,2017(13).

[7]Charalambides M N, Goh S M, Lim S L, et al. The analysis of the frictional effect on stress-strain data from uniaxial compression of cheese[J].Journal of Materials Science,2001,36(9):2313-2321.

[8]Gamonpilas C,Charalambides M N, Williams J G, et al. Predicting the Mechanical Behaviour of Starch Gels through Inverse Analysis of Indentation Data[J]. Applied Rheology,2010,20(3):33283.

[9]Goh S M, Charalambides M N,Williams J G. On the mechanics of wire cutting of cheese[J].Engineering Fracture Mechanics, 2005,72(6):931-946.

[10]Ikeda S, Sangu T, Nishinari K. Comparative studies on fracture characteristics of food gels subjected to uniaxial compression and torsion.[J].Food Science & Technology Research,2003,9(4):372-377.