分段错极排列的PMLSM磁阻力研究
2018-04-27王明杰邱洪波杨存祥田高伟
王明杰,武 洁,邱洪波,杨存祥,田高伟
(郑州轻工业学院,郑州 450002)
0 引 言
永磁直线同步电机(以下简称PMLSM)具有推力大、响应速度快、定位精度高等优点,在矿井提升系统、交通运输、精密加工等直线运动场合具有广阔的应用前景[1-3]。但PMLSM中存在的磁阻力影响电机的伺服性能,如何抑制PMLSM中的磁阻力是许多学者研究的重要内容之一[3-11]。
PMLSM中的磁阻力包括电机端部开断动子所受的端部力和电枢开槽动子所受的齿槽力。抑制磁阻力常用的方法有斜槽斜极[4]、优化电枢长度[5-6]和槽型[7]、添加辅助极铁心[8]、优化永磁体长度[9]、改变永磁体排列方式[10]等,通常一种方法仅能抑制磁阻力的一个分量,以上方法均针对电机结构方面的研究。因此本文先用解析法研究磁阻力最小时的电机结构尺寸,再用有限元准确计算磁阻力的大小,两者结合提高计算效率。在改变电枢结构方面,文献[5]假设电机为两半无限长单端铁心结构,用解析法分析单端端部力的傅里叶级数正余弦分量基波幅值,给出了优化电枢长度抑制电机端部力普遍规律的解析式,适用于电机设计初始阶段。文献[8]采用在距电枢端部一定距离处添加辅助极铁心补偿电机端部力,但有限元分析时辅助极铁心的位置及尺寸难以用解析式确定。在改变磁极排列方式方面,文献[4]采用斜极抑制电机齿槽力,斜极后对磁极加工和贴片安装造成困难,且磁场分析为三维场,计算耗时耗力。考虑到斜极后三维磁场计算的复杂性,文献[11]采用分段斜极方法研究分段数与斜极角对推力波动的影响,结合二维有限元计算三维非对称运动模型,简化了复杂的三维场计算。文献[12-13]采用轴向分段错极排列方法较好地削弱旋转电机磁阻转矩,而直线电动机结构的特殊性及参数计算方法与之不同。本文对已有的PMLSM模型进行优化,采用优化电机端齿宽度方法减小端部力,端齿宽度取决于端部力最小时的电枢长度,对磁极进行横向分段并依次偏移一定距离削弱齿槽力基波,分段后可看作是多台电机的并列运行,研究磁阻力与偏移距离、磁极分段数、谐波次数的关系,有限元结果表明,模型优化后的电机磁阻力得到了较好的削弱。
1 分段错极排列PMLSM结构
1.1 磁极分段结构
分段错极排列是沿PMLSM横向将磁极等分成N段,各段磁极依次偏移Δx距离,如图1所示。分段错极排列后,电枢结构不变,与电枢耦合的各段磁极发生了偏移。与斜极相比,电机结构简单,加工方便,电机场量分析仍可视为二维场,避免了复杂的三维场计算。
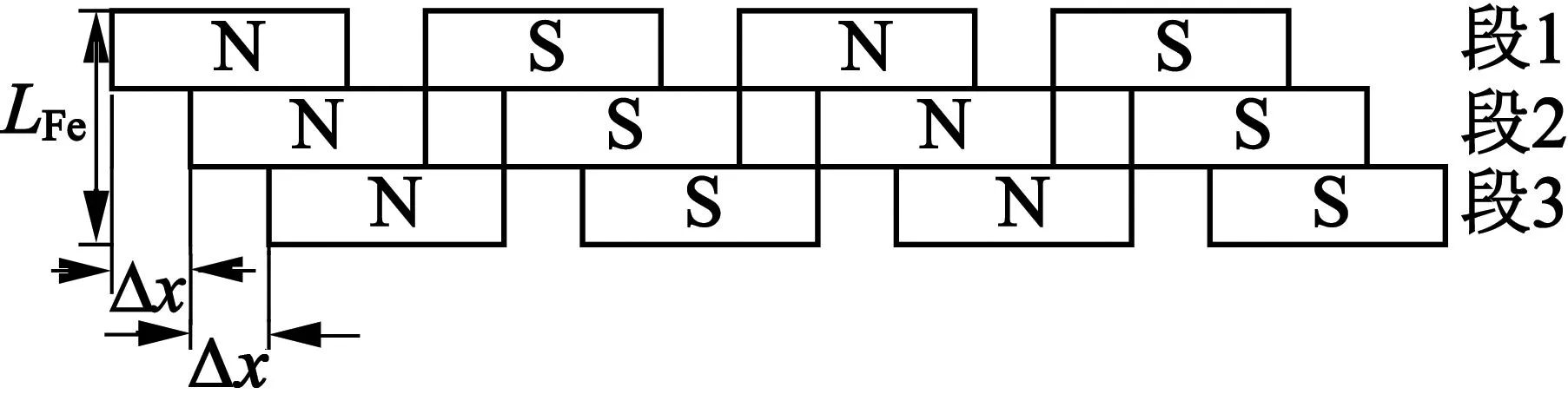
(a) 磁极排列结构图

(b) 电机三维图
1.2 磁场解析模型
磁极分段后,忽略磁路饱和效应和段间横向边缘效应的影响,则各段磁极产生的磁场是相互独立的,在空间上依次偏移Δx距离,因此只需计算其中一段磁场即可知其他各段磁场的分布。以图2所示解析模型为求解区域,齿槽区对气隙磁场的影响用卡氏系数等效,采用等效磁化强度法求解气隙磁场区域,将永磁体等效成磁化强度分布函数M(x)。

图2 解析模型求解区域
PMLSM各分区域的数学模型如下。
气隙区域:
(1)
永磁体区域:
(2)
Jp(x)=×M(x)
(3)
在各区域交界面边界条件满足:
(4)

根据式(1)~式(4)推导出气隙磁场区域的解析式:
(5)

(6)
式中:Cn,Dn为气隙区域磁密系数,k=π/τ,τ为极距。
各段磁极空间上依次偏移Δx距离,则第t段磁密:
(7)
1.3 磁场结果分析
以一台6极18槽的PMLSM为分析模型,主要结构尺寸:极距39mm,齿距t=13mm,永磁体长lm=27 mm,气隙5 mm,横向长114 mm,动子有效长度239 mm。以横向磁极分段数N=2为例,每段磁极沿纵向依次偏移6.5 mm,根据式(5)~式(7)和有限元法得到的气隙磁密波形如图3所示。可以看到两种方法波形基本一致,解析法的段1和段2磁密(图中ANA表示)分别对应有限元法的段1和段2磁密(图中FEM表示),两种方法得到的段1和段2磁密空间位置都相差6.5 mm。有限元法考虑了齿槽效应对气隙磁场的影响,波形更接近于实际情况。磁极分段错极排列后,各段磁极产生的磁场在空间位置上依次偏移Δx距离,相当于多台PMLSM并列运行,因此横向磁极分段并依次偏移,其作用等效于永磁体的斜极,将永磁体斜极的三维场转化为二维场分析模型,简化了电机制造工艺,磁极安装方便,省去了耗时耗力的复杂三维场计算,计算效率提高。
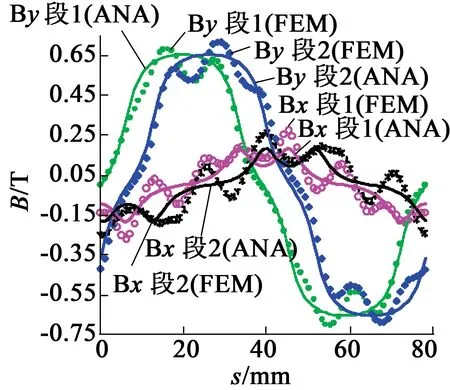
图3 解析法和有限元法得到的气隙磁密
2 PMLSM结构优化
结构优化先从削弱电机端部力入手,PMLSM端部力是由电机端部开断造成的。在短次级长初级的PMLSM中,磁阻力主要为齿槽力,周期为一个齿距;在短初级长次级的PMLSM中,磁阻力主要为端部力,周期为一个极距。通常短初级长次级的端部力大于其齿槽力[14],因此本文中18槽6极的PMLSM端部力大于齿槽力,PMLSM电枢左右两端所受端部力的傅里叶级数表达式[6]:
(8)
(9)
电枢所受总端部力:
(10)
由上式知,当L=(n+0.5)τ时,Fend最小。
采用优化端齿宽度方法减小端部力,其作用相当于优化动子长度。确定端齿宽度可通过优化动子长度前后相减得到,也可通过以端齿宽为参数变量参数化计算得到。PMLSM磁阻力可等效为周期性模型时动子所受齿槽力和动子等效成矩形块时所受端部力的叠加,以端齿宽度a为变量,采用有限元法,动子等效成矩形块。由理论知只优化电枢长度时,端部力应在L=(6+0.5)τ附近处达到最小值,可得端齿宽理论值a=12.25 mm。实际分析时端部力不可能完全消除,有限元法得到的端部力随a的关系如图4所示。由图4可知,当端齿宽a为14.2 mm时端部力最小,端部力由原来的88.7 N减小到9.5 N,同时磁阻力由原来的121.6 N减小到46.1 N,此时动子长度L=(6+0.6)τ,优化后PMLSM结构如图5所示。

图4 磁阻力与动子端齿宽度的关系

图5 优化后PMLSM结构图
3 分段错极排列PMLSM的齿槽力和端部力
3.1 齿槽力计算分析
以上述优化结构图5为分析模型,此时PMLSM磁阻力主要为齿槽力,将横向长度为LFe的PMLSM磁极沿横向等分成N段,每段铁心横向长为LFe/N,每段磁极依次偏移Δx距离,每段PMLSM参数计算仍可用二维场计算,各段PMLSM所受的齿槽力[15]:
第t段:
总齿槽力为各段齿槽力的叠加:
(11)
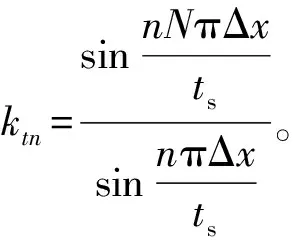



图6 各分段磁阻力曲线(N=3)
3.2 端部力计算分析
分段错极排列后对PMLSM端部力也起了一定的抑制作用。分段错极排列后电机的总端部力:
(12)
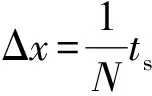
(13)

(14)
端齿优化前总磁阻力中的基波和二次谐波主要有端部力产生,端齿优化后端部力基波已大幅度削弱,又对于18槽6极τ=3ts,因此总磁阻力的三次谐波由齿槽力的基波产生,而齿槽力基波已由式(11)削弱。根据式(14),只考虑总磁阻力的前三次谐波时可表示:
(15)
式中:第一、二项分别为端部力基波、2次谐波,第三项为齿槽力基波,a1,a2,a3为分段后谐波相位偏移距离。
各次谐波系数ksn随分段数的关系如图7所示,可以看到ksn≤1,随着分段数的增加,各次系数ksn逐渐变小,使总端部力变小,最终趋于一恒值。由式(15)知,分段错极排列后,端部力谐波系数ksn的前两次谐波系数分别削弱了磁阻力的基波和2次谐波,2次谐波系数削弱磁阻力程度大于基波系数削弱程度,从而进一步减小了磁阻力。当N≥2时,端部力3次谐波系数为零,此时3次谐波主要为齿槽力。

图7 端部力谐波系数与分段数的关系
3.3 磁阻力计算结果分析
不同分段下PMLSM的总磁阻力、齿槽力分量、端部力分量波形随位置及其分段数如图8所示,图中N1,N2等表示磁极分段数分别为1,2时的曲线。由图8可知:
1) 图8(a)、图8(b)中不管是总磁阻力还是总齿槽力分量均以齿距为周期,呈现3次谐波,为式(15)中的第三项,分析原因同图6。端部力基波因端齿优化后大幅度削弱,端部力由主要作用变为次要作用,齿槽力起主要作用。图8(c)中总端部力在一个极距内有两个周期,呈现2次谐波,因端部力基波虽得到了较好的削弱,而对端部力的2次谐波削弱程度并不大,因此2次谐波在端部力中起主要作用,2次谐波为式(15)中的第二项。
2) 分段错极排列后,总磁阻力、端部力、齿槽力随着N的增大而减小,最终趋于在某一范围内波动。当N=2时,齿槽力基波已得到了较好的削弱,使磁阻力幅值下降程度较大;当N=3时,磁阻力幅值仍有略微下降;N≥3以后下降程度已不明显。由图8(c)知,N≥2时,端部力变化已不明显,N≥2时的端部力由未分段前N=1时的9.5 N减小到3.5 N,且相对于优化动子前原样机的88.7 N端部力,减小了96%。
3)N=3时,磁阻力由分段前N=1的46.1 N减小到9.4 N,且相对于优化端齿宽度前原样机121.6 N的磁阻力,减小了92.3%,较好地削弱了磁阻力。因此N=3为合理的磁极分段数。

(a)总磁阻力
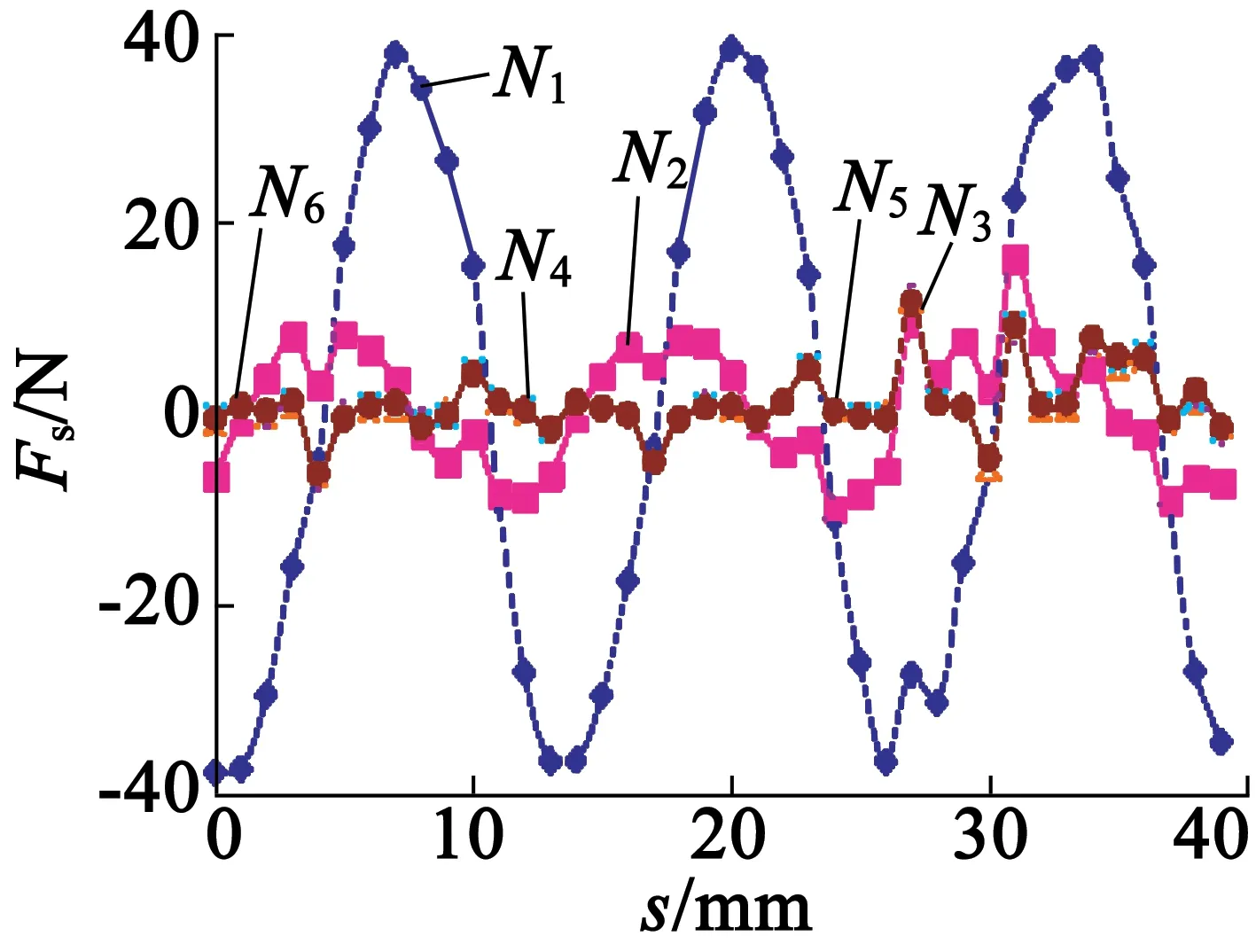
(b)总齿槽力分量

(c)总端部力分量
4 结 语
1) 将PMLSM磁阻力中的端部力和齿槽力分量分别单独考虑,根据优化动子长度方法确定电枢端齿尺寸,较好抑制了端部力的基波。
2) 采用错极分段排列方法抑制电机的齿槽力,探讨了磁阻力与偏移距离、分段数、谐波次数之间的关系。磁极分段偏移后削弱了齿槽力基波,同时对端部力有进一步削弱作用,端部力2次谐波的削弱
程度大于基波的削弱程度,但2次谐波在端部力中仍起主要作用。当N≥2时,端部力中不存在3次谐波。
3) 随着分段数的增加,磁阻力削弱程度已不明显,趋于在某一范围内波动。有限元结果表明,N=3时,电机的磁阻力由原样机的121.6N下降到9.4N,证明了所用研究方法的有效性。
[1] 王明杰,程志平,焦留成.组合磁极无槽PMLSM正弦磁场分析[J].电机与控制学报,2015,19(4):34-39.
[2] 王明杰,程志平,焦留成.永磁直线电动机的稳态参数计算分析及有限元验证[J].微特电机,2014,42(7):5-8.
[3] 司纪凯,汪旭东.永磁直线同步电机出入端磁阻力齿槽分量分析[J].电机与控制学报,2008,12(5),550-554.
[4]HWANGIC,JANGKB.AstudyonthecharacteristicsanalysisaccordingtooverhangandskewofpermanentmagnetinPMLSM[J].ProceedingofInternationalConferenceonElectricalMachinesandSystems2007:1255-1258.
[5] 潘开林,傅建中,陈子辰.永磁同步直线电机的磁阻力分析及其最小化研究[J].中国电机工程学报,2004,24(4):112-115.
[6]ZHUZQ,XIAZP.Reductionofcoggingforceinslotlesslinearpermanentmagnetmotors[J].IEEEProc-Electr.PowerApplications,1997,144(4):277-282.
[7]ZHUYW,KOODH.Detentforceminimizationofpermanentmagnetlinearsynchronousmotorbymeansoftwodifferentmethods[J].IEEETransactionsonMagnetics,2008,44(11):4345-4348.
[8]ZHUYW,CHOYH.Detentforcereductioninpermanent-magnetlinearsynchronousmotorutilizingauxiliarypoles[C]//2009 8thInternationalSymposiumonAdvancedElectromechanicalMotionSystems&ElectricDrivesJointSymposium,2009:1-6.
[9]LIMKC,WOOJK.Detentforceminimizationtechniquesinpermanentmagnetlinearsynchronousmotors[J].IEEETransactionsonMagnetics,2002,38(2):1157-1160.
[10]BIANCHIN,BOLOGNANIS.ReductionofcoggingforceinPMlinearmotorsbypole-shifting[J].IEEEProc.-Electr.PowerApplications,2005,152(3):703-709.
[11] 蔡炯炯,卢琴芬.PMLSM推力波动抑制分段斜极方法研究[J].浙江大学学报(工学版),2012,46(6):1122-1127.
[12]FEIW,LUKPCK.Anewtechniqueofcoggingtorquesuppressionindirect-drivepermanent-magnetbrushlessmachines[J].IEEETransactionsonIndustryApplications,2010,46(4):1332-1340.
[13]ZHUZQ,RUANGS.AnalysisofcoggingtorqueinbrushlessMachineshavingnonuniformlydistributedstatorslotsandsteppedrotormagnets[J].IEEETransactionsonMagnetics,2005,41(10):3910-3912.
[14]JUNGIS,YOONSB.Analysisofforcesinashortprimarytypeandashortsecondarytypepermanentmagnetlinearsynchronousmotor[J].IEEETransactionsonEnergyConversion,1999,14(4):1265-1270.
[15] 王秀和.永磁电机[M].北京:中国电力出版社,2007:83-84.
