基于永磁无刷轮毂电机的矢量跟踪观测器研究

樊生文，杨 濛，李睿智

(北方工业大学，北京 100041)

0 引 言

永磁电机正越来越多地用于各种高性能应用领域，如航空航天、军事、汽车、工业和家用产品。其中，永磁无刷轮毂电机在电动汽车上的应用前景十分广阔，其成本低、控制简单，除了可以降低车辆结构复杂性、增加车体空间等优点，未来还可以实现线控底盘、四轮独立驱动等前沿汽车驱动方案。

轮毂电机的矢量控制精度取决于转子位置的精度。通常，转子位置信息可以通过高精度传感器获得，例如安装在电动机轴上的增量式编码器或旋转变压器。然而，这些传感器不仅增加了系统成本，长度和尺寸，而且大大降低了系统的可靠性。在采用增量编码器的情况下，还需在起动时通过初始定位算[1]法来获得初始位置角。

近年来，已经开发了各种无传感器方法作为替代安装传感器的方案，其大致分类为基于反电动势[2]、高频注入[3]。然而，大量文献说明，就目前而言大多数无传感器算法不能保证电机在整个速度范围和扭矩范围内的特性[4]，尤其是在电机低速和满载的情况下，而这个工况在以轮毂电机为基础的电动汽车上是很常见的，对电动汽车来说，任意的起停都是满载和低速的情况。而且这些无传感器技术还没有成熟地使用，于电动汽车驱动器上[5]。

在参考文献[11-12]中提出了一些补偿霍尔传感器安装误差的方法。文献[12]中有一种自动校准的方法，其可以得到实际霍尔信号状态的切换点，利用迭代程序确定理想点和实际点之间的偏差，并将所得到的实际状态转变值在初始化时存储在查找表中方便调试。由于其主要算法是基于平均速度的，所以在变速度运行下性能会受到影响。

在参考文献文献[13-14]中，使用矢量跟踪观测器，从霍尔传感器的信号中准确提取出转子位置信息，在参考文献[15]中，提出了一种改进的方法，以去耦合法消去转子位置信号中的固有干扰项。这种方法跟踪能力滞后。然而，由于观测器是基于电机的模型设计的，位置估计容易受到系统惯性和负载变化的影响，以上文献未考虑负载变化下的情况。

本文提出了一种基于平均转子速度的矢量跟踪观测器，其具有平均速度的前馈输入，可以估计出高精度的转子位置信息，而且其动态性能也相对较好。观测器的基本结构类似于矢量跟踪锁相环(PLL)，它由相位检测器和滤波器的比例积分控制器(PI)组成。相位检测器用来提取位置估计误差信号，位置误差是从定子侧得出的反电动势向量与估计的反电动势向量之间的相位差得出的。然后，PI控制器使位置误差快速收敛到零，并且适当地校正前馈的平均速度，包括由传感器的速度变化引起的系统误差。本方法已在DSP28335上实现，并用于汽车应用的永磁轮毂电机驱动器中。

1 转子位置估计

1.1 基于二阶平均转子速度的位置估算与误差校准

高精度的转子位置信息可以通过基于平均转子速度[6-10]的方法进行估计，其中六个扇区根据霍尔传感器的信号状态进行分类。如图1所示，即假设扇区内的转子速度是恒定的，当前和上一个扇区中的平均速度是均匀的，则转子速度可以近似：

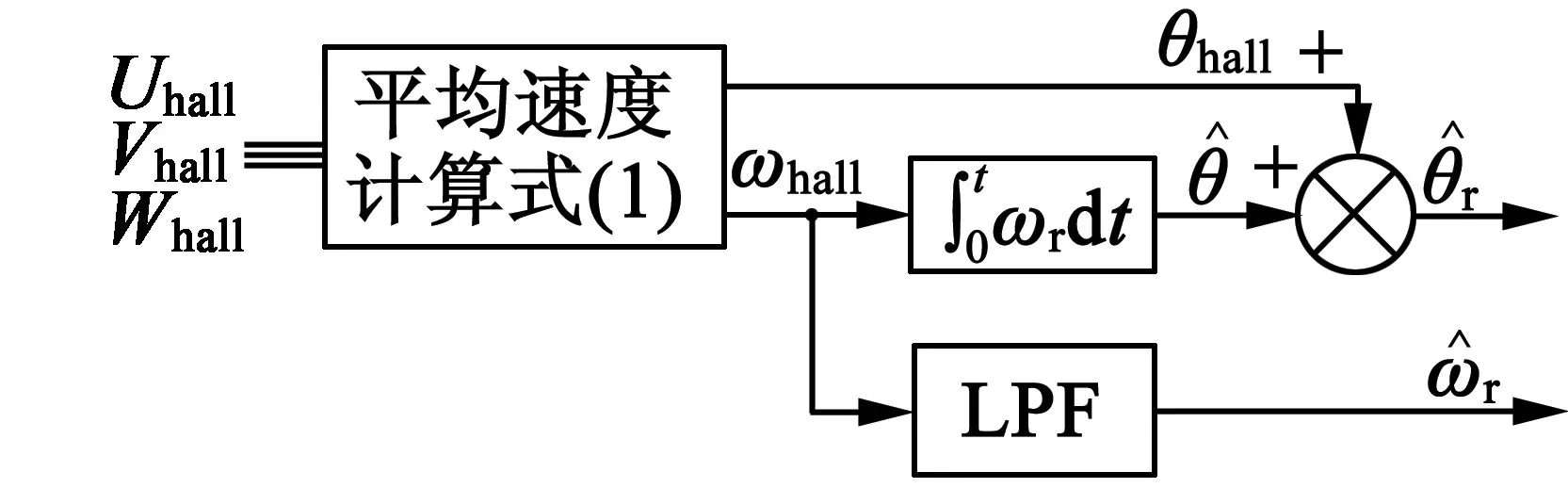
图1 一阶平均速度算法

(1)

Δt是经过上一扇区所用的时间。然后，通过积分运算式(2)来估计转子位置：

(2)

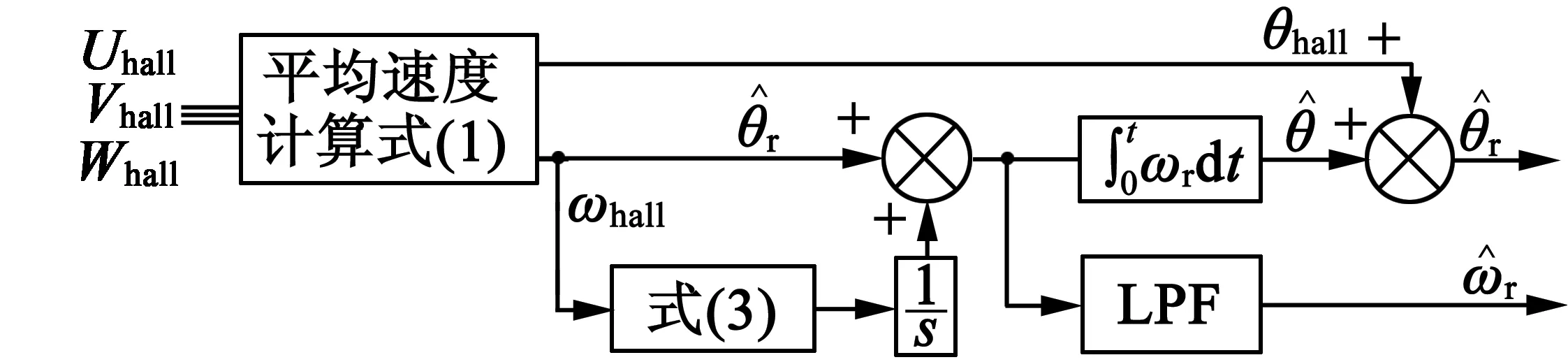
图2 二阶平均速度算法

电机平均加速度的概念，平均加速度的计算公式如下：

(3)

(4)

若霍尔传感器在安装时是精确无误的，则从式(2)获得的转子位置在电机稳态运行时是精确的。但是由于电机制作的工艺不一样，霍尔传感器的安装或多或少都会出现误差，除此之外，还存在电机变速运行时的估计误差，所以，在实际运行中会存在一定的估计误差，并且会产生电流失真和转矩脉动大的现象。

图3 霍尔安装误差信号对比

(5)

式中：EUV为霍尔U相的下降沿所对应的线反电动势，EUVm为线反电动势的幅值。由此可依次标定出每个霍尔信号边沿的实际信号，也就是误差信号，依次测得的实际的变换角度如表1所示。

表1 霍尔传感器的安装误差

其中角度差已经在图3中说明，在后面实验部分会看到经过校准和没有经过校准的对比波形。

电机的瞬态过程中也可在实践中通过式(2)～式(4)提高变速过程中的位置估计误差，但因为每个扇区的平均速度和平均加速度并不能实时地表示电机的运行状态，所以还会存在角度误差。

1.2 基于向量跟踪的位置估计

为了提高基于二阶平均转子速度方法的性能，本文提出了一种具有前馈二阶平均速度输入的矢量跟踪位置观测器，其具有类似于文献[12]中提及的矢量跟踪锁相环的结构，也是基于电机定子侧的数学模型而提出的。

图4 永磁无刷轮毂电机正弦波矢量控制框图

本文采用具有霍尔传感器的永磁无刷轮毂电机正弦波矢量控制方案，位置和速度估计器的平均速度和解耦电流控制回路的控制框图如图4所示。静态参考系中的模型方程可以推导如下：

(6)

(7)

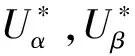
因为数字控制系统具有较高的采样频率，所以可以将控制系统离散形式表示为式(6)。如果估计的转子位置和速度与实际值相同，则可以获得以下等式：

(8)

式中：k是采样时刻。式(8)的右侧表示由永磁体外转子建立的反电动势估计方程。左侧代表从定子电路计算的参考反电动势，并将反电动势量通过低通滤波器(LPF)进行滤波， LPF可以将噪声最小化和相位延迟最小化。滤波器输出的参考反电动势向量表达式如下：

(9)

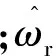
(10)

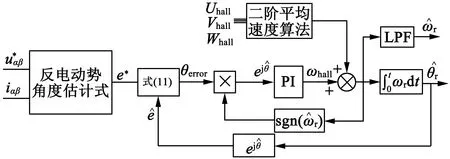
图5 矢量跟踪位置观测器结合霍尔传感器的控制框图

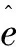
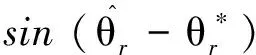
(11)

式中：θerror是位置估计误差。然后，通过位置估计器的PI控制器来获得式(7)中的校正速度ωerror，使得式(8)的结果值收敛为零：

(12)

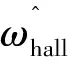
(13)

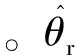
虽然式(12)的速度校正算法不能在零速时或极低速进行校正，但是可以通过初始位置定位[3]和速度估计算法式(7)中的平均速度ωhall来提供有用的位置信息。

1.3 位置估计算法验证

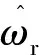
图5 矢量跟踪位置观测器结合霍尔传感器的控制框图

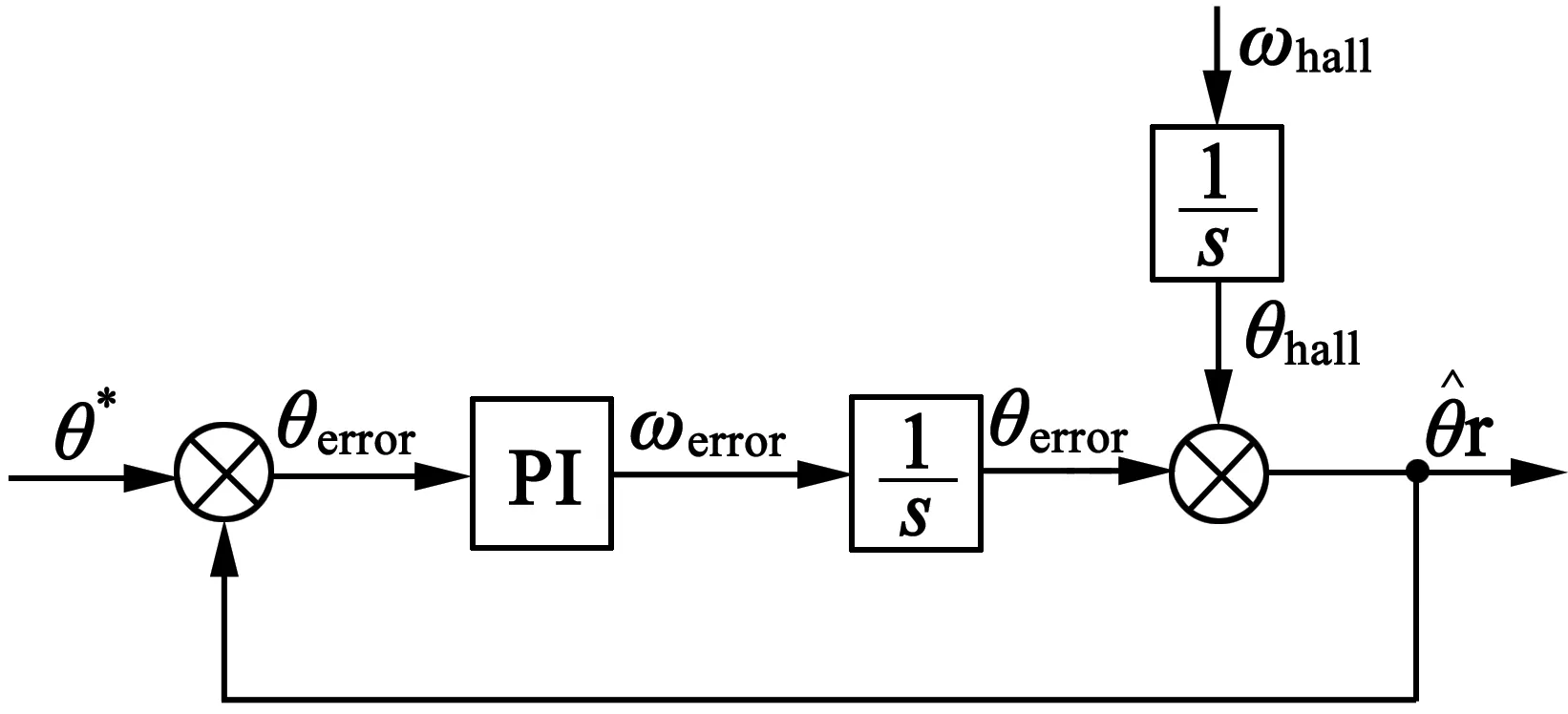
图6 角度前馈输入二阶模型

(14)

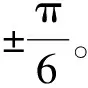
图7 速度前馈输入二阶模型

(15)

式中：kp和ki分别是PI控制器的比例和积分增益。PI控制器的参数设定对于位置估计的动态性有很大的影响。其PI参数可以由文献[2]中方法整定。

1.4 针对变化负载时的算法改进

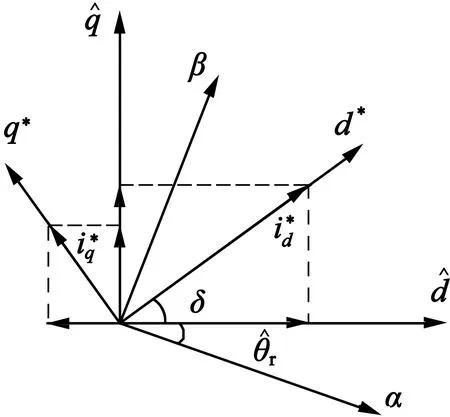
图8 电机的d-q模型下的负载角

(16)

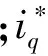
从图8中可以看出，如果负载角δ(即电动机负载引起的位置误差)值较小，则式(16)可以变换：

≃

(17)

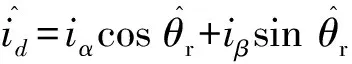
(18)

(19)

在式(19)中，等号左侧反映的是负载角δ的信息。因此，负载角可以通过以下PI型控制器进行估计：

(20)

最终的位置估计误差为式(11)的位置误差和式(20)的负载角之和。正如式(21)中所示，将式(20)的估计负载角加到式(12)的速度校正中，则所提出的矢量跟踪观测器即可以通过校正负载角误差来提高位置估计性能。

(21)

2 实验结果

为验证所提出的矢量跟踪位置估计器的可行性，本文已进行了若干实验。在实验中，通过与基于平均速度的算法的结果进行比较而得出结论。

实验驱动器的总体控制方案如图4所示，已经在DSP28335上实现。变频器的PWM频率设置为20 kHz。电流控制和矢量跟踪位置观测器均在PWM周期内同步执行。测试电机是用于汽车的表贴式永磁轮毂电机，它用3个霍尔传感器进行速度和位置检测。表1为由这些错位引起的每个扇区中的测量绝对位置的角度偏差。另外采用1024线的旋转变压器同轴安装，用于比较估计位置和实际转子位置。驱动系统的其他规格如表2所示。

表2 永磁无刷轮毂电机参数

图9为在100 r/min速度和8 A负载稳态下的相电流波形、实际位置和估计位置。图9(a)为未经过霍尔校准的实验波形，可以看出电流波形明显失真，尤其在每个π/3扇区结束时位置突然校正。

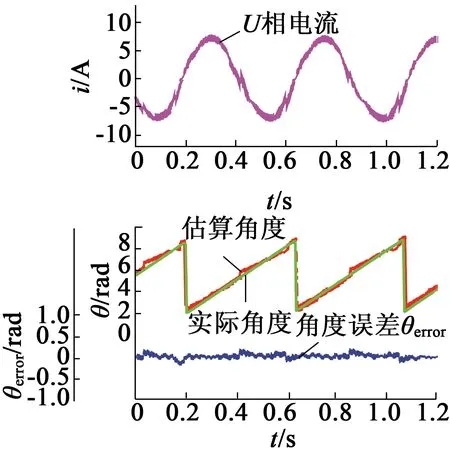
(a) 未经过校准的实验波形

(b) 经过校正后的实验波形

这是由于平均速度误差和霍尔传感器的安装误差引起的。而图9(b)是经过校准后的实验波形，电流波形失真得到较好的抑制，也没有出现位置突然校正的情况。

(a) 二阶平均速度算法

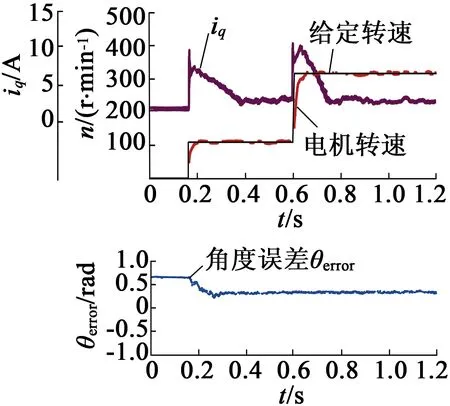
(b) 改进算法

采用本文方法所得出的实验波形如图10(b)所示，从初始位置误差将估计位置误差迅速收敛为零， 并且与平均速度方法相比，几乎没有出现q轴电流较大波动，而且电流恢复的斜率基本保持不变。

图11为带载情况下与图8同样的调速情况下的波形。图11(a)为基于二阶平均速度算法所得到的实验波形，可以看出，电机起动时的位置误差还是不能快速收敛到零；在电机达到稳态后还存在角度误差的波动情况；q轴电流也可以迅速达到给定，但在稳态时存在明显的波动，从而使转速也有波动。

图11(b)为采用改进算法后的波形。可以看出，角度误差在起动时迅速收敛到零，达到稳态和突加载加速的情况下误差波动也较小，q轴电流与电机转速波动都相比减小了很多。因此也证明了所提出的算法具有良好的动态性能。

(a) 二阶平均速度算法

(b) 改进算法

图12为电机在200r/min速度下从空载到额定载电流的负载阶跃响应，图12(a)为没有采用负载补偿算法的波形，图10(b)为采用负载补偿算法的实验波形。当突加载时，图12(a)中估计误差增加与负载角增加瞬间都增加，在加入负载角补偿算法如图12(b)所示的实验波形中，在突加载的瞬间很好的稳定状态下可以较好的消除该估计误差。

(a) 二阶平均速度算法

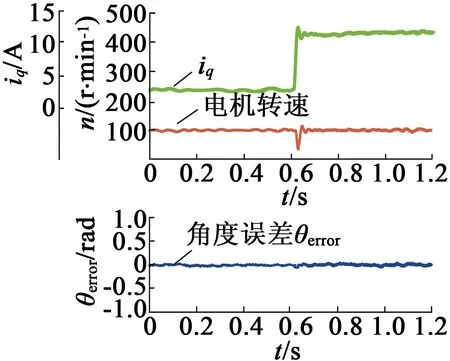
(b) 改进算法

3 结 语

本文提出了一种矢量跟踪位置观测器的控制算法，旨在具有低精度霍尔传感器的永磁无刷轮毂电机驱动器中高精度地估算出转子位置，可以更好地应用于电动汽车电机控制中，降低驱动器的成本。所提出的方法具有类似于位置锁相环的结构，其具有基于二阶平均速度的前馈输入，也有通过反电动势估计出的转子位置信息。这个算法可以在轮毂电机低速状态和高速状态下检测到较为精准的转子位置信息。在零速度以上时，位置估计误差快速收敛到零，可以得到高精度的位置信息；在轮毂电机处于变速运动时，经过校准后的传感器通过此算法可以比较准确地得出转子位置信息；并且在空载调速、额载调速和突加载等实验条件下进行波形分析。波形分析表明，相比二阶平均速度算法，位置误差动态可以快速收敛到零，稳态波动相对较小。另经过霍尔传感器安装误差的校准后，可以观测到电流波形在每个扇区切换时畸变情况有明显的改善。总之，本文提出的矢量跟踪位置观测器改进算法可以成功地应用于永磁无刷轮毂电机驱动器中。

[1] 郭农生,周元钧.改进的永磁同步电机转子初始位置检测方法[A].第十五届中国小电机技术研讨会论文集[C]//2010:68-72

[2] BALAZOVIC P,FILKA R.Sensorless PMSM control for H-axis washing machine drive[C]//Power Electronics Specialists Conference.IEEE,2008:4237-4242.

[3] 王子辉,陆凯元,叶云岳.基于改进的脉冲电压注入永磁同步电机转子初始位置检测方法[J].中国电机工程学报,2011,31(36):95-101.

[4] 李永东,朱昊.永磁同步电机无速度传感器控制综述[J].电气传动,2009,39(9):3-10.

[5] 徐征,李铁才.准无位置传感器永磁同步电动机驱动系统中霍尔传感器位置检测误差的分析及解决方案[J].中国电机工程学报,2004,24(1):168-173.

[6] 董窈窈.采用低分辨率位置传感器的正弦波永磁同步电机控制系统[D].济南：山东大学,2007.

[7] 栾捷,陈阳生.基于低分辨率位置传感器的电动汽车用轮毂电机的控制[J].机电工程,2013,30(5):524-529.

[8] 曾风平,郑成勇,章跃进.基于开关型霍尔位置传感器的永磁同步电动机正弦波驱动[J].微特电机,2010,38(8):56-58.

[9] 卢彬芳,黄进,张耀中.高性能永磁同步电动机的低成本简易正弦波控制[J].微特电机,2015,43(5):70-73.

[10] 邹继斌,徐永向,于成龙.正弦波无刷直流电机的新型转子位置检测方法[J].中国电机工程学报,2002,22(12):47-49.

[11] DONG L,JATSKEVICH J,HUANG Y,et al.Fault diagnosis and signal reconstruction of hall sensors in brushless permanent magnet motor drives[J].IEEE Transactions on Energy Conversion,2015,31(1):1-14.

[12] SHIN S C,CHOI C H,YOUM J H,et al.Position control of PMSM using jerk-limited trajectory for torque ripple reduction in robot applications[J].Oxford Review of Education,2012,16(1):2400-2405.

[13] CAPPONI F G,DE DONATO G,DEL FERRARO L,et al.AC brushless drive with low-resolution Hall-effect sensors for surface-mounted PM Machines[J].IEEE Transactions on Industry Applications,2006,42(2):526-535.

[14] GOUGANI M,JATSKEVICH J,CHAPARIHA M.Locking and synchronizing controller for hall-sensor driven motors：US20150061547[P].2015-03-15.

[15] HARKE M C,DE DONATO G,CAPPONI F G,et al.Erratum to implementation issues and performance evaluation of sinusoidal, surface-mounted pm machine drives with hall-effect position sensors and a vector-tracking observer[J].IEEE Transactions on Industry Applications,2008,44(2):565-565.

[16] 卢东斌,欧阳明高,谷靖,等.电动汽车永磁无刷轮毂电机磁场定向控制[J].电机与控制学报,2012,16(11):76-83.

[17] KIM S Y,LEE W,RHO M S,et al.Effective dead-time compensation using a simple vectorial disturbance estimator in PMSM drives.IEEE Transactions on Industrial Electronics,2010,57(5):1609-1614.

[18] KERKMAN R J,LEGGATE D,SCHLEGEL D W,et al.Effects of parasitics on the control of voltage source inverters[J].IEEE Transactions on Power Electronics,2003,18(1):140-150.

[19] 王艳霞.基于模型预测的永磁同步电机直接转矩控制及负载角限制[J].微特电机,2016,44(8):126-130.